基于局部熵的超聲信號閾值降噪方法

張 洪，張 郁，王通德

(1.江南大學機械工程學院江蘇省食品先進制造裝備技術重點實驗室，江蘇 無錫 214122；2.國網電力科學研究院江蘇南瑞恒馳電氣裝備有限公司，江蘇 無錫 214161)

0 引言

超聲檢測作為五大常規無損檢測技術之一，是目前國內外應用最廣泛、使用頻率最高且發展較快的一種無損檢測技術，已經被國家相關法規列為特種設備檢驗的必要環節[1]。然而在金屬材料的超聲檢測中，例如奧氏體不銹鋼等粗晶材料的晶界會對超聲波起散射作用，造成結構噪聲，從而使缺陷信號被噪聲污染甚至湮沒[2]。因此，采用合適的信號處理方法，抑制金屬晶粒引起的結構噪聲，有利于缺陷回波信號的識別，從而提高檢測結果的正確率。

目前，超聲信號的降噪方法一般依據噪聲信號與缺陷信號的頻域概率分布差異，通過傅里葉變換、小波變換、經驗模態分解(Empirical Mode Decomposition, EMD)等方法對信號進行分解，然后再對分解的結果進行降噪處理。傅里葉變換無法同時在時域和頻域上獲得較好的局部化性質，目前已經很少使用。小波變換則需要選擇小波基函數和分解層數，是非自適應性的[3]，降噪效果受參數選擇的影響較大。而EMD及其改進方法不需要先驗獲得信號和噪聲的統計特性，即可自適應地分解信號，適用范圍更廣。

使用EMD及其改進方法將信號分解為多個本征模態函數(IMF)分量之后，還需要對這些IMF分量做進一步的降噪處理。目前常用的IMF分量降噪方法沿用了小波領域的閾值降噪法[4-5]，此方法對高斯白噪聲的降噪效果較好，但對結構噪聲的降噪效果則不佳。基于此，本文針對傳統IMF分量降噪方法的不足，提出了基于局部熵的金屬材料超聲信號閾值降噪方法。

1 基本原理

1.1 CEEMDAN算法

EMD可以自適應地將非線性、非平穩的信號分解為一系列頻帶不同的IMF分量和殘余分量之和，并且將IMF分量按照瞬時頻率的差異從高到低排列起來。雖然EMD克服了小波變換的最優參數選擇問題，但是其存在模態混疊現象，限制了信號分解的效果。

集合經驗模態分解(Ensemble Empirical Mode Decomposition, EEMD)是一種噪聲輔助數據分析方法，通過在原信號中多次添加白噪聲，分別進行EMD分解，然后對多次EMD分解得到的IMF分量取平均值，求得最終的IMF分量。這種方法雖然能夠有效地解決模態混疊問題，但分解過程中添加的白噪聲無法完全消除，且平均次數的多少嚴重影響了信號的重構誤差。即使增加計算次數可以減小重構誤差，但也會嚴重影響分解的計算效率。

具有自適應白噪聲的完整集成經驗模態分解 (CEEMDAN)方法在EEMD的基礎上進一步改進，在EMD分解的每個階段添加自適應的白噪聲，可在較少的平均次數下使重構誤差幾乎為0。因此CEEMDAN不但可以解決EMD分解的模態混疊問題，同時也可以解決EEMD分解的重構誤差與平均次數相矛盾的問題。

CEEMDAN分解算法的具體步驟如下：

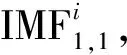
(1)

殘余分量r1(t)=x(t)-IMF1。

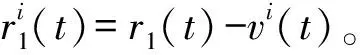
(2)

殘余分量r2(t)=r1(t)-IMF2。

3)重復上述的分解步驟n次，且每一次分解后都會得到IMFi分量和殘余分量，直到滿足EMD分解的終止條件。最終得到的分解結果為

(3)

1.2 熵理論

信息論中，信息熵用事件發生的概率的倒數來表示該事件的信息[6]。設pi(i=1,2,3,…,n)為系統某一狀態發生的概率，則該狀態所具有的信息量可用如下公式定義：

(4)

式(4)中，概率pi具有如下性質

(5)

使用所有狀態含有的信息量的數學期望值作為系統的信息熵

(6)

2 超聲信號的局部熵閾值降噪算法

使用CEEMDAN分解信號得到如式(3)所示的IMF分量，再對IMF分量進行閾值降噪。傳統方法依據信號的長度與方差等參數來確定降噪閾值，但此方法未對CEEMDAN分解進行優化，用于IMF分量降噪時效果不佳。本文針對IMF分量的降噪方法進行優化，使用信號的熵作為閾值的選取依據。

然而，直接使用式(6)計算出的信息熵，反應的是整體信號的信息量，無法用來衡量某一個信號點的含噪狀態，也就難以作為閾值的選取依據。因此改進信息熵的計算方法，提出能夠反映信號局部性質的局部熵，并以此作為信號閾值降噪的依據。

2.1 一維信號的局部熵

一維信號局部熵的計算方法類比了圖像處理領域的二維信號局部熵[7]，建立尺寸為w的窗口，則一維信號x(t)在時間坐標軸上t0處的鄰域為(t0-w/2,t0+w/2)。根據式(6)，計算這個鄰域內信號的熵值Sw(t0)，作為信號點x(t0)在窗長度w下的局部熵。對每個信號點做如上處理，即可獲得所有信號點的局部熵Sw(t)。

不同信號的局部熵數值范圍可能不同，為了提高局部熵在閾值降噪中的通用性，對局部熵做線性歸一化處理,使其分布范圍為0到1之間：

(7)

局部熵反映了信號的離散程度，在均勻區域中局部熵比較大，在異質區域中局部熵比較小[7]。常見的缺陷可等效為圓柱狀缺陷[8]，對超聲波的反射次數較少，因此缺陷回波屬于均勻信號，局部熵較大；而金屬晶粒對超聲波起多次散射作用，因此晶粒造成的結構噪聲屬于異質信號，局部熵較小。這個缺陷回波信號與結構噪聲信號之間的局部熵差異，即為本文閾值降噪算法的理論依據。

2.2 超聲信號的局部熵校正

如圖1所示，超聲波聲場中存在主聲束和副瓣聲束[9]。而超聲波的能量主要集中在半擴散角θ0以內，即主聲束的范圍為2θ0。2θ0以外為副瓣聲束，其含有的能量在波源附近衰減很快[1]。因此本文僅考慮主聲束被材料晶粒散射而造成的結構噪聲。

設超聲波傳播時間為t，超聲波在金屬材料中的傳播速度為c，金屬材料單位面積內的晶粒數目為Zs。在時刻t，主聲束的波陣面為一個球冠面，則球冠最大開口部分圓的半徑r=ctsinθ0，球冠的高h=ct(1-cosθ0)，由此計算出的球冠的面積為Scq=2πrh=2πc2t2sinθ0(1-cosθ0)，此時超聲波的主波束所能檢測到的晶粒數目為：

Q=ZsScq=2πZsc2t2sinθ0(1-cosθ0)

(7)

式(7)中只有t為變量，其它參數為常量。可見超聲波傳播的時間t越久，所檢測到的晶粒數量就越多。

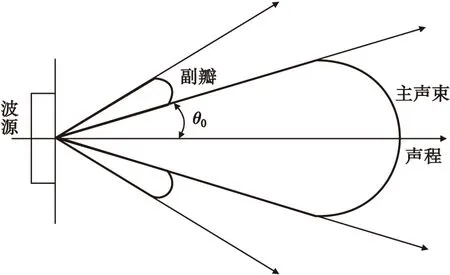
圖1 波源聲束示意圖Fig.1 Diagram of ultrasonic beam source

根據文獻[8]中的式(13)可知，晶粒的數目越多，由晶粒造成的散射回波也就越多，即結構噪聲越雜亂。因此超聲波的傳播時間較短時，所能檢測到的晶粒數目較少，結構噪聲的雜亂度較低，局部熵也就較大；反之超聲傳播時間越長，結構噪聲的局部熵也就越小。

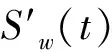
(8)

為了使校正后局部熵的數值仍然分布在0到1之間，需要對其再做一次如式(7)的線性歸一化處理。

(9)

式(9)中，E(·)為數學期望。

2.3 局部熵閾值降噪算法

使用CEEMDAN分解信號x(t)，得到分量IMFi(i=1,2,…,n)和殘余分量r(t)。使用相關系數法[10]確定需要降噪的IMF分量：計算IMFi與原信號x(t)之間的相關系數，并取相關系數為中等程度相關及以上的分量IMFj(j∈i)作為需要降噪的分量。

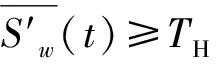
(10)

式(10)中α為降噪系數，其函數的形式如圖2所示。

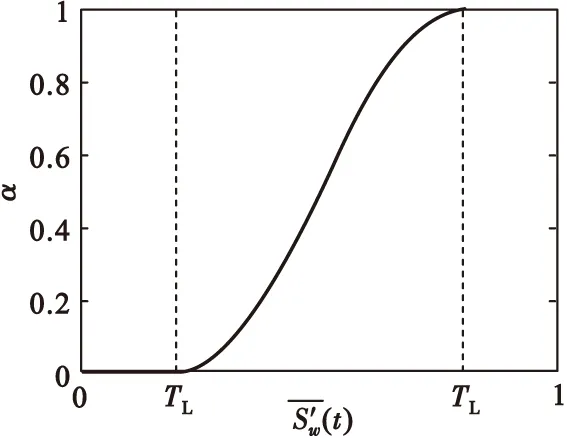
圖2 降噪系數α函數圖Fig.2 Function diagram of De-noising coefficient α

則降噪后的IMF分量為

(11)

經降噪后得到的超聲信號x′(t)為

(12)

2.4 超聲信號的消噪方法

基于局部熵的超聲信號閾值降噪方法的具體實施步驟如下：

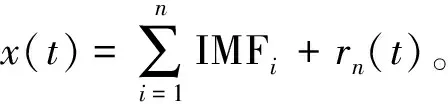
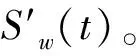
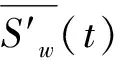
4)計算IMFi與原信號x(t)之間的相關系數，選取中等程度相關及以上的分量IMFj(j∈i)作為需要降噪的分量。

3 試驗與分析

3.1 數據來源

目前通用的仿真方法，無法控制超聲信號在不同時刻的局部熵數值，因此也就無法證明2.2節理論的正確性。因此，本文使用實測的超聲信號為研究對象，分別對比了局部熵校正前與校正后的降噪效果、局部熵最優計算窗口長度與一般窗口長度下的降噪效果、傳統方法與本文方法的降噪效果，以證明本文提出方法的有效性。

實測信號如圖3所示，檢測儀器為友聯PXUT-910超聲探傷儀，檢測對象為壓力容器鋼X型對接焊縫，焊縫厚度為108 mm，焊縫寬度為50 mm，檢測標準為JB/T4730.10-2010。

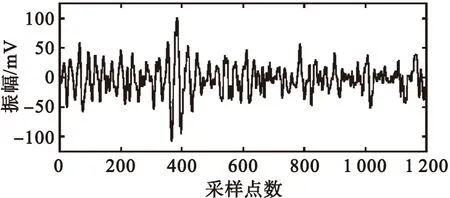
圖3 實測超聲信號Fig.3 Measured ultrasonic signal

3.2 降噪效果對比

常用的降噪效果評價指標為信號的信噪比和均方差，但根據其定義[11]，這兩個指標的計算過程必須以純凈信號為基準。純凈信號為僅含有用波形，且不含有噪聲波形的信號，仿真試驗中可以很容易地獲取這個信號，但實測信號實驗中卻很困難。因此本文以信號降噪前后的波形對比圖作為標準，來評判降噪方法的有效性。

將實測超聲信號x(t)進行CEEMDAN分解，分解后得到的IMF分量見圖4。從圖4中可以看出，超聲信號x(t)被分解為9個IMF分量，但其中哪些分量的噪聲屬于結構噪聲仍然未知，需要使用相關系數法來確定。計算IMFi(i=1,2,…,9)與原信號之間的相關系數，結果如表1所示(保留3位小數)。

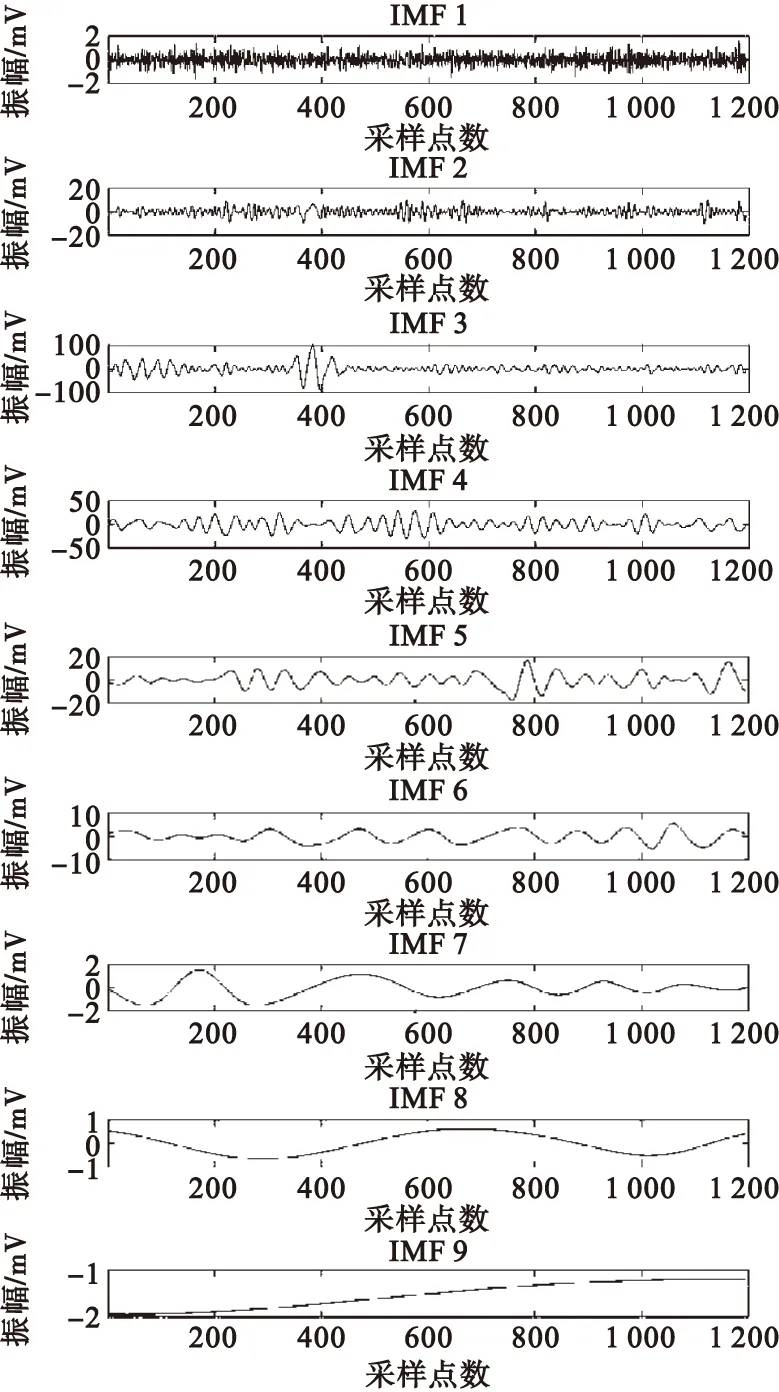
圖4 CEEMDAN分解結果Fig.4 Decomposition results of CEEMDAN

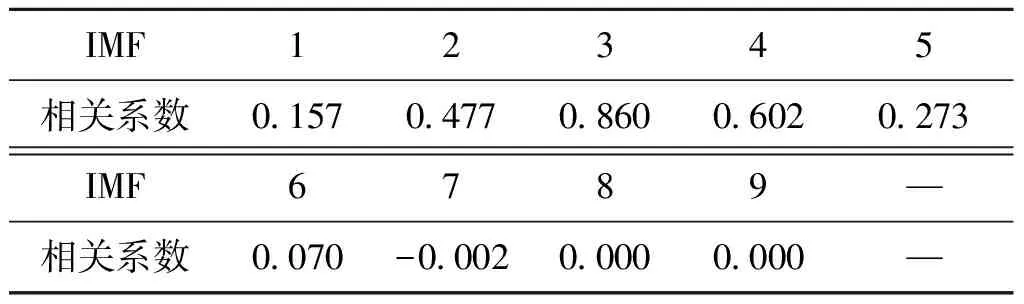
IMF12345相關系數0.1570.4770.8600.6020.273IMF6789—相關系數0.070-0.0020.0000.000—

根據Pearson相關系數定義的中等程度相關，取相關系數為0.4及以上的IMF分量為需要降噪的分量。由表1中的相關系數值可知，結構噪聲所在的分量為IMFj(j=2,3,4)，這些分量需要按照本文提出的方法進行處理；IMF1為高斯白噪聲分量，不屬于本文研究內容，使用傳統方法[12]進行處理;IMFk(k=5,6,…,9)為趨勢分量，不作處理。

3.2.1局部熵的校正及其降噪效果

初步選取局部熵計算窗口長度w為100，計算圖3所示超聲信號x(t)的局部熵，并依據式(7)作線性歸一化處理,結果如圖5所示。

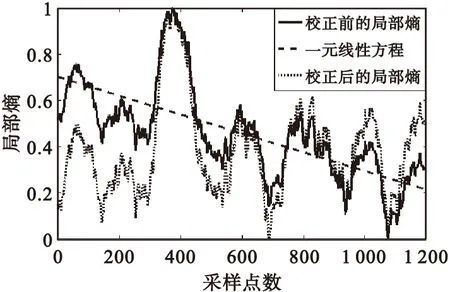
圖5 局部熵及其校正Fig.5 Local entropy and its correction

從圖5中校正前的局部熵可以看出，局部熵的大體趨勢隨著時間的增長而減小，這符合2.2節中關于超聲波傳播特性對局部熵數值影響的分析。

為了消除局部熵隨著時間增長而減小的趨勢，對校正前的局部熵進行一元線性回歸分析，得到一元線性方程，然后從校正前的局部熵數值中減去這個趨勢方程，即可得到校正后的局部熵。一元線性方程及校正后的局部熵如圖5所示。

分別以校正前與校正后的局部熵為降噪參數，取閾值TH=0.8，TL=0.2,使用式(10)、式(11)對IMFj(j=2,3,4)進行降噪，再使用式(12)重構IMF分量得到降噪后的信號，降噪效果如圖6所示。

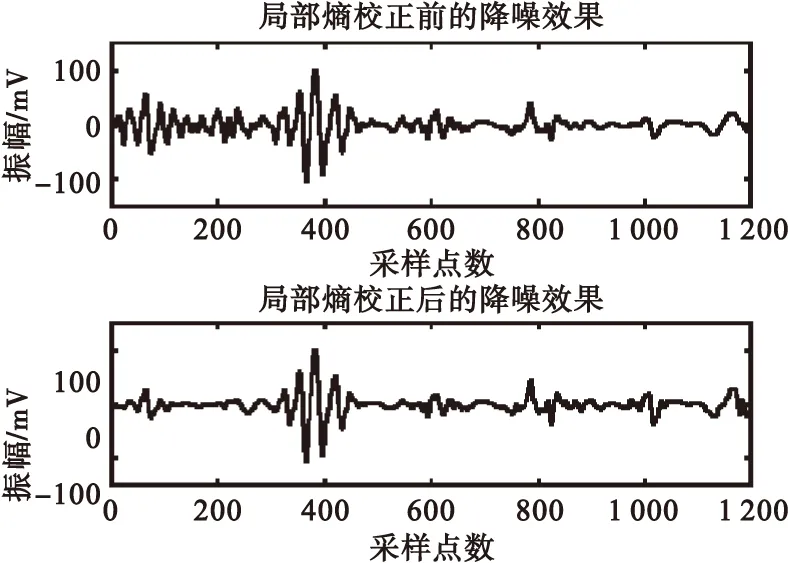
圖6 局部熵校正前后的降噪效果Fig.6 De-noising effect by local entropy before and after correction

從圖6中可以看出，使用校正前的局部熵作為降噪參數時，雖然信號后半部分的降噪效果較好，但前300個采樣點的信號降噪效果較差。而使用了本文提出的方法校正局部熵之后，再進行降噪時，不論是信號的前半部分還是后半部分，都得到了較好的降噪效果。

3.2.2窗口長度的選取及其降噪效果

窗口長度w決定了每個時刻的局部熵是由多少個信號點計算而來的。為了研究不同的窗口長度對降噪效果的影響，分別取w為50，100，166，200，250，300時，計算超聲信號x(t)的局部熵，然后進行降噪處理，其中w=166是依據式(9)計算出的最優窗口長度。降噪后的信號波形如圖7所示。

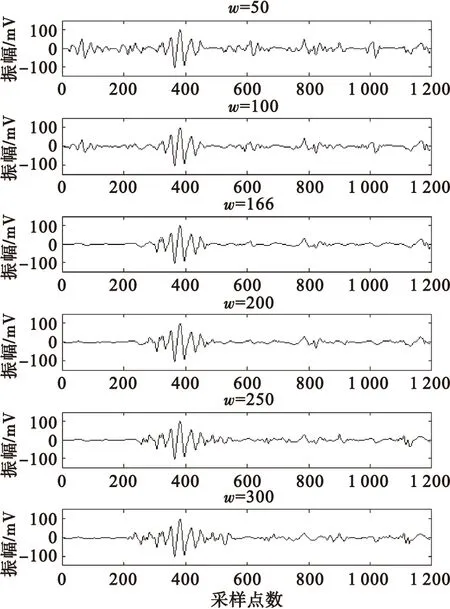
圖7 不同窗口長度下局部熵的降噪效果Fig.7 De-noising effect of local entropy under different window length

當窗口長度過小時，窗口內的信號只能存在較少的幅值狀態，也就是相均質。這導致了部分噪聲信號的局部熵值偏大，在進行降噪處理時被當作了有用信號，從而被保留下來。從圖7所示降噪對比圖中可以看出，當w=50時，信號中仍保留有較多的噪聲；而當w從50擴大到166時，降噪的效果越來越好。

當窗口長度過大時，有效信號附近的噪聲信號則更容易被保留下來。計算這些噪聲信號的局部熵時，由于窗口長度過大，部分有效信號也會被包含進來，這部分有效信號會拉高噪聲信號的局部熵，從而使噪聲被保留下來。如圖7所示，當w從166擴大到300時，有效信號兩端的噪聲信號越來越多。

依據本文提出的方法選取最優窗口長度(w=166)，再進行信號的降噪處理，從結果中可以看出，不論是整體的降噪效果，還是有效信號附近的降噪效果，都得到了提升。

3.2.3與傳統方法的對比

使用小波變換及CEEMDAN結合傳統的閾值算法對信號進行降噪，與本文提出的方法作對比。其中小波變換選取db4小波函數將信號x(t)分解到第5層，采用Rigrsure方法確定閾值，選取硬閾值函數和軟閾值函數中降噪效果較好的一組結果作為對照；CEEMDAN方法的閾值和閾值函數選取方式同上。三種方法的降噪效果如圖8所示。

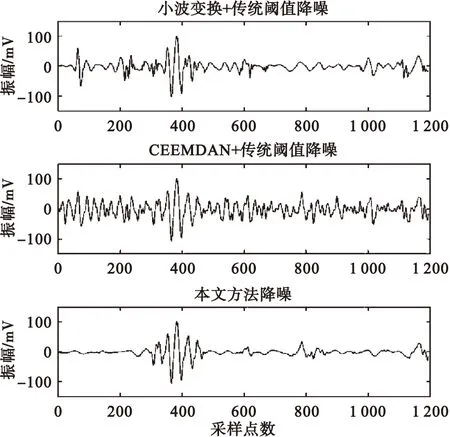
圖8 不同方法的降噪效果Fig.8 De-noising effect of different methods

從圖8中可以看出，小波變換結合傳統閾值算法的降噪方法，對結構噪聲占主導的超聲信號有一定的降噪作用，但是降噪后的信號仍保留有較多的噪聲。CEEMDAN結合傳統閾值算法的降噪方法，由于沒有針對IMF分量的特性進行優化，因此降噪效果極為有限。而本文提出的方法，不僅在整體的降噪效果上優于小波變換，而且對有效信號的保留也更加完整，更有利于信號的分析與識別。

4 結論

本文提出了基于局部熵的超聲信號閾值降噪方法。該閾值降噪方法首先計算出一維超聲信號的局部熵，并根據超聲波在金屬材料中的傳播原理，對局部熵的數值進行校正，同時還確定了局部熵的最優計算窗口長度選擇方法。最后結合局部熵，提出了適用于IMF分量的閾值降噪公式，用以取代現有的IMF分量閾值降噪方法。試驗結果表明，在對實測超聲信號的降噪過程中，經過該閾值降噪方法處理過的信號，能夠有效地消除絕大部分的結構噪聲，且盡可能地保留了有用信號，降噪效果優于小波變換及CEEMDAN結合傳統閾值算法的降噪方法。