一種可觀測度分析方法及在匹配模式研究中的應用

王海亮，石志勇，李國璋，王志偉

(1.陸軍工程大學石家莊校區，河北 石家莊 050003；2.解放軍第96864部隊，河南 洛陽 471000)

0 引言

為提高捷聯慣導系統的導航精度，導航前必須對慣性器件(陀螺儀和加速度計)進行誤差標定，標定過程中匹配模式的選擇是影響濾波估計效果的主要因素之一。為了進一步優化捷聯慣導在線標定方案，研究不同匹配模式對在線標定結果的影響是十分必要的。系統的可觀測性是影響標定效果的決定因素，因此需要分析不同匹配模式下系統的可觀測性以選擇最優的匹配模式。文獻[1]基于卡爾曼濾波算法及最小二乘理論，分別研究了速度加姿態匹配、比力匹配、角速度匹配模式下的彈載慣導標定效果，但沒有分析不同匹配模式優劣；文獻[2]通過仿真分析采用速度匹配模式時，失準角估計效果不理想，而采用速度加姿態匹配時，當載體進行特定機動時可有效提高系統可觀測性，但并沒有進行理論上的分析；文獻[3]在對比四種典型的可觀測度分析方法基礎上，基于最小二乘理論，設計了改進的局部和全局可觀測度分析方法；文獻[4]針對彈載慣導誤差在線標定對可觀測度的實際需求，提出一種基于受約束最優化的可觀測度分析方法，并對其準確性及有效性進行了數學證明，但是該方法不具備普遍適用性。

本文針對捷聯慣導系統在線標定過程中的匹配模式選擇問題，提出一種新的可觀測度分析方法，并采用該方法研究了三種不同匹配模式下的在線標定效果。

1 基于最小二乘估計理論的可觀測度分析方法

在設計卡爾曼濾波器之前，必須對系統進行可觀測性分析，可觀測性反映了系統在一定時間內通過觀測量確定系統狀態的能力，其估計的精度與狀態量的可觀測度密切相關[5]。下面從系統初始狀態的最小二乘估計角度，考慮系統的可觀測度，為簡化分析，考慮如下離散線性系統：

(1)

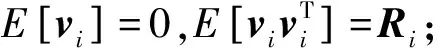
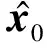
(2)

將式(2)兩端對x0求偏導可得：

(3)

令式(3)等號左端為零，則能夠計算得出x0的最小二乘估計為：

(4)

設估計誤差：

(5)

將式(4)帶入式(5)可得：

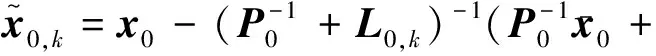
(6)

將zk=HiFi,0x0+vi帶入式(6)得：

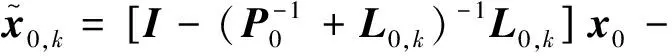
(7)

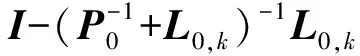
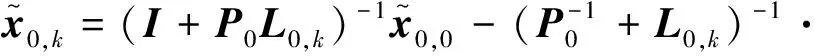
(8)

式(8)等號右側第一項表示估計誤差的衰減程度，第二項表示觀測噪聲對估計誤差的影響，在此忽略觀測噪聲的影響，則式(8)可簡化為：

(9)

由式(9)可得，矩陣(I+P0L0,k)-1的對角線元素反映的是狀態變量中各分量的估計誤差相對于各初始估計誤差的衰減程度。定義系統各狀態量的可觀測度指標為(I+P0L0,k)-1中相對應的對角線元素，即：

ηi={diag[(I+P0L0,k)-1]}i

(10)

由上述可觀測度定義可知：|ηi|越靠近零，說明估計誤差的衰減越明顯，則對應狀態量的可觀測度越大；|ηi|越靠近1，說明估計誤差衰減越小，對應狀態量的可觀測度就越小。

2 不同匹配模式下的在線標定濾波模型

2.1 速度加姿態匹配的在線標定濾波模型

根據文獻[6]給出的系統誤差方程構建系統濾波模型如下：

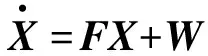
(11)

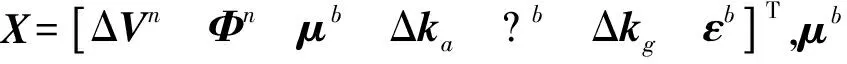
(12)

(13)

矩陣F中各子矩陣的定義參照文獻[7]。

2.2 速度加姿態加位置匹配的在線標定濾波模型

狀態空間模型的建立同式(11)，由于在速度加姿態匹配的基礎上增加了位置觀測量，因此狀態變量改為：X=[ΔVnΦnΔpnμbΔkabΔkgεb]T，其中Δpn即表示位置誤差，觀測量

狀態矩陣改為：

(14)

其中各子矩陣的定義參照文獻[8]。

觀測測矩陣改為：

(15)

2.3 速度加位置匹配的在線標定濾波模型

狀態空間模型的建立同樣參照式(11)，具體參數定義如下：

狀態變量改為X=[ΔVnΔpnμbΔkabΔkgεb]T，觀測量改為狀態矩陣設置參照式(12)，觀測矩陣改為：

(16)

3 仿真分析

3.1 初始條件設置

為了滿足卡爾曼濾波要求，對式(11)離散化，且載體機動路徑設置參照文獻[7]。具體濾波參數設置如下：

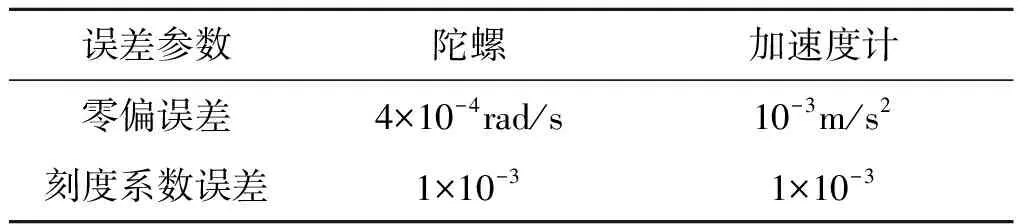
表1 慣性器件誤差參數設置

3.2 仿真結果分析

采用本文可觀測度分析方法對以上三種匹配模式下的在線標定模型進行可觀測度分析，結果如表2所示。

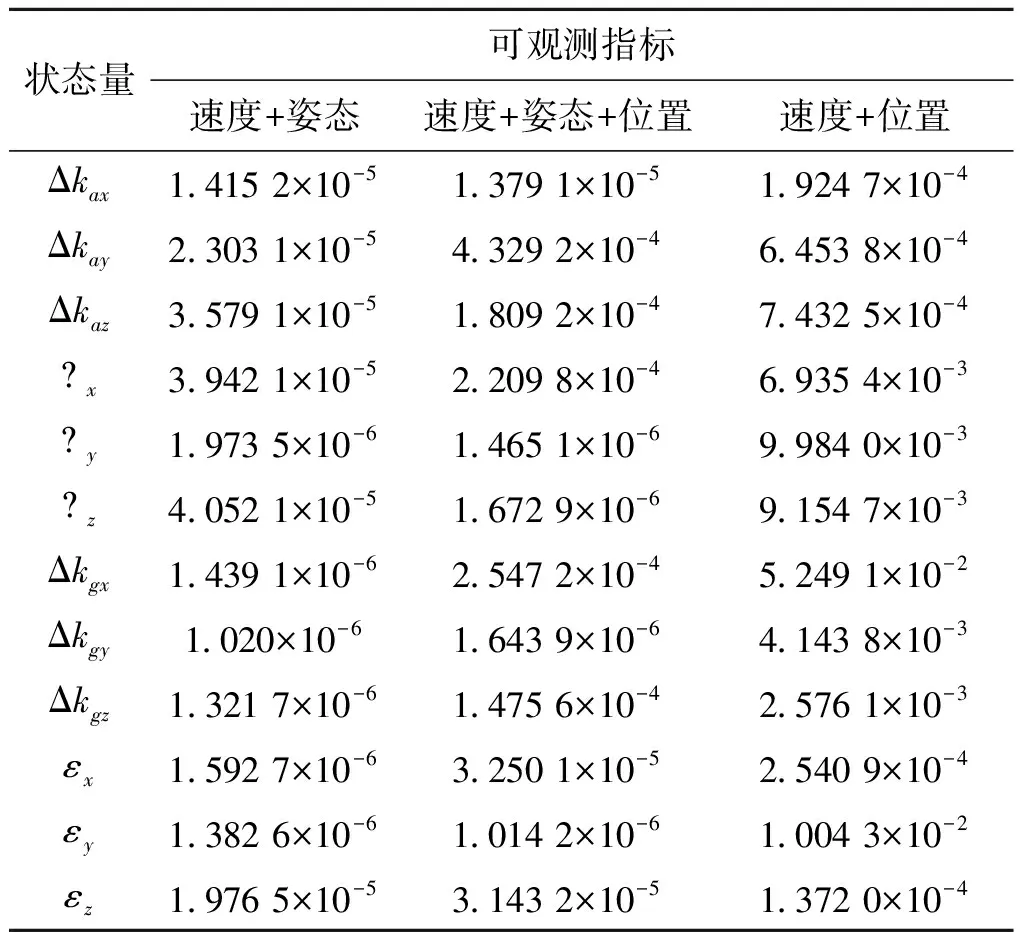
表2 三種匹配模式下各狀態量可觀測指標

由表2可知：當機動方式相同時，采用速度加姿態匹配模式時各誤差參數的可觀測度指標都很小，都具有較高的可觀測度。采用速度加姿態加位置匹配模式時，可觀測指標有稍微增大，說明各誤差參數可觀測度有所降低，這是由于增加了位置觀測量導致計算量增大，收斂時間會有所延長導致的。當采用速度加位置匹配模式時，可觀測指標大幅增大，狀態參數可觀測度普遍較低，尤其是Y軸、Z軸加速度計零偏，X軸陀螺刻度系數誤差，Y軸陀螺漂移的可觀測度最差。

為了驗證本文提出的可觀測度分析方法的準確性，利用Matlab軟件平臺分別對三種匹配模式下在線標定過程進行仿真，采用標準卡爾曼濾波算法對誤差參數進行估計，慣性器件各誤差參數的濾波估計結果如圖1、圖2所示，其中直線表示預先設定值，曲線表示濾波估計值(濾波估計曲線中實線表示速度加姿態匹配的估計值，點畫線表示速度加姿態加位置匹配的估計值，虛線表示速度加位置匹配的估計值)。

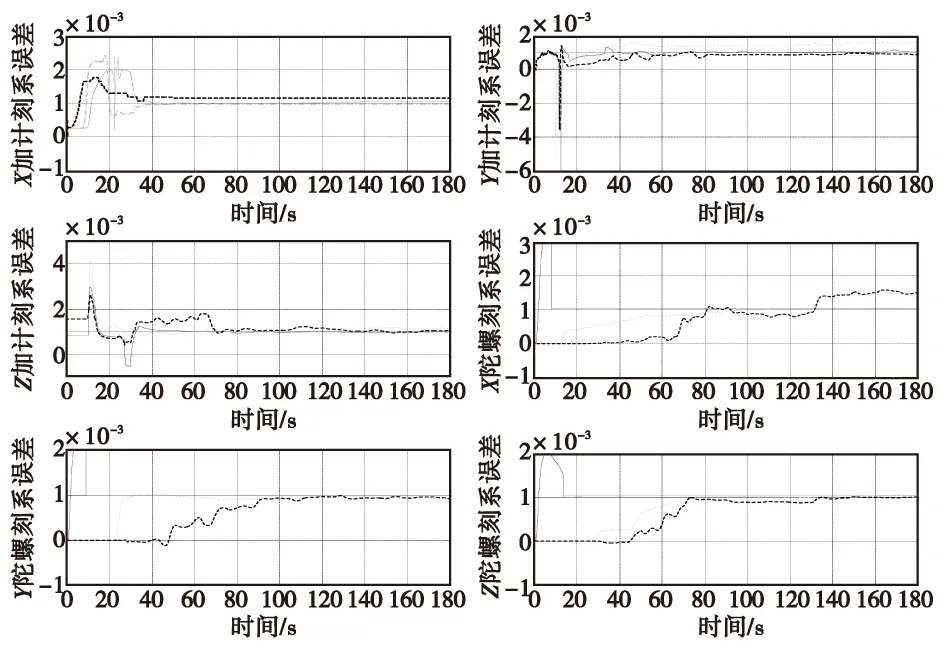
圖1 加速度計和陀螺刻度系數誤差估計曲線Fig.1 Accelerometer and gyro scale factor error estimation curve

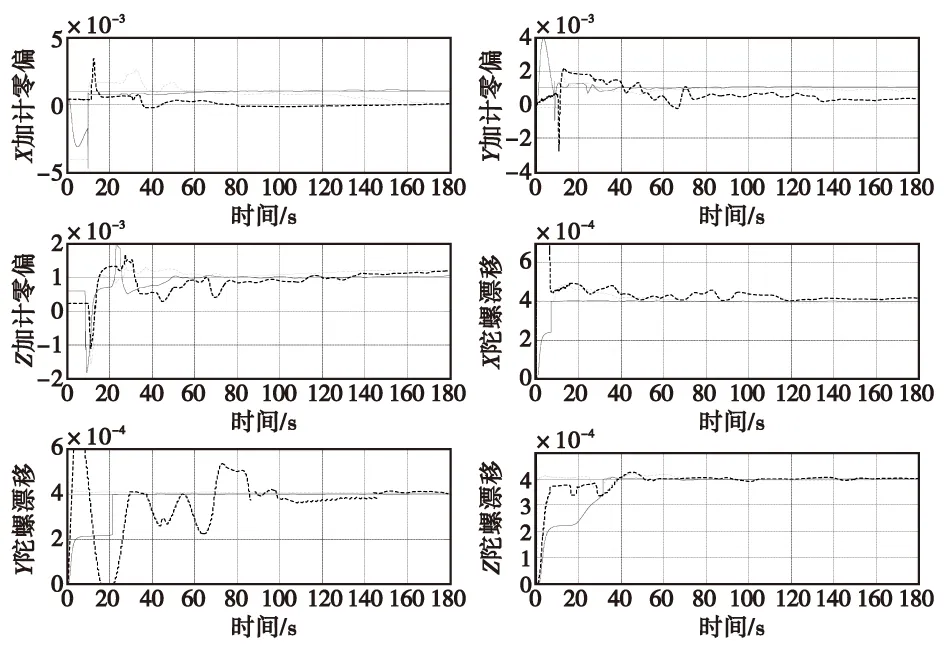
圖2 加速度計零偏和陀螺漂移估計曲線Fig.2 Accelerometer bias and gyro drift estimation curves

由圖1、圖2可以看出，采用速度加姿態匹配模式時，慣性器件12個誤差參數的標定精度都比較高，且除Z軸加速度計零偏之外的11個誤差參數的收斂時間都比較短；采用速度加姿態加位置匹配模式時，慣性器件12個誤差參數的標定精度與采用速度加姿態匹配時相當，但收斂時間明顯增加，尤其是X軸、Z軸陀螺刻度系數誤差收斂時間都達到了80 s以上；當采用速度加位置匹配時各誤差參數的估計精度較低，且收斂時間也比較長，特別是X軸陀螺刻度系數誤差、X軸加速度計零偏、Y軸加速度計零偏及Y軸陀螺漂移甚至無法完成標定。因此，標定結果與表2所示三種匹配模式下12個誤差參數的可觀測指標是相符的，證明了新的可觀測度分析方法是可靠的。

為進一步考察不同觀測量對標定效果的影響，下面分別從標定精度和收斂時間兩方面對標定結果進行分析。當濾波基本達到穩定后，對140～180 s時間段內的濾波估計值求平均值作為該次仿真的估計值，且為了消除隨機噪聲的影響，重復仿真試驗5次，將5次仿真估計值再求平均值作為最終的誤差估計值并求出誤差標定的相對精度(相對精度=|估計值-預設值|÷預設值)，結果見表3。同時，將不同匹配模式下各誤差參數的收斂時間總結見表4。

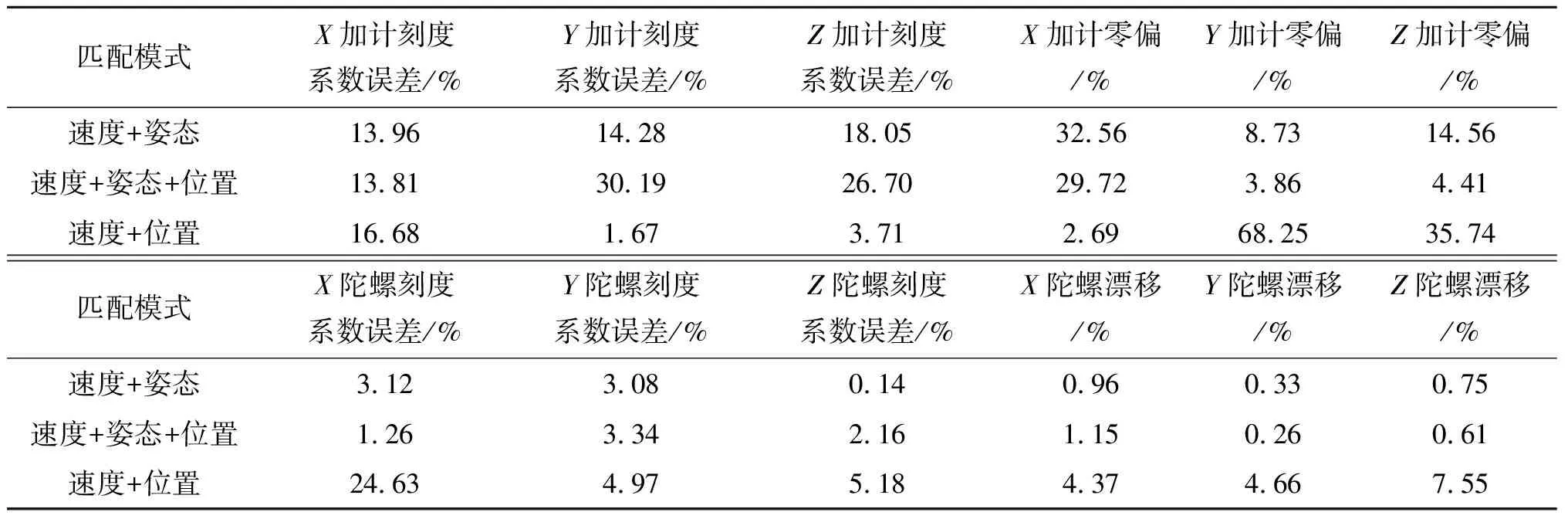
表3 不同匹配模式下各誤差參數標定相對精度

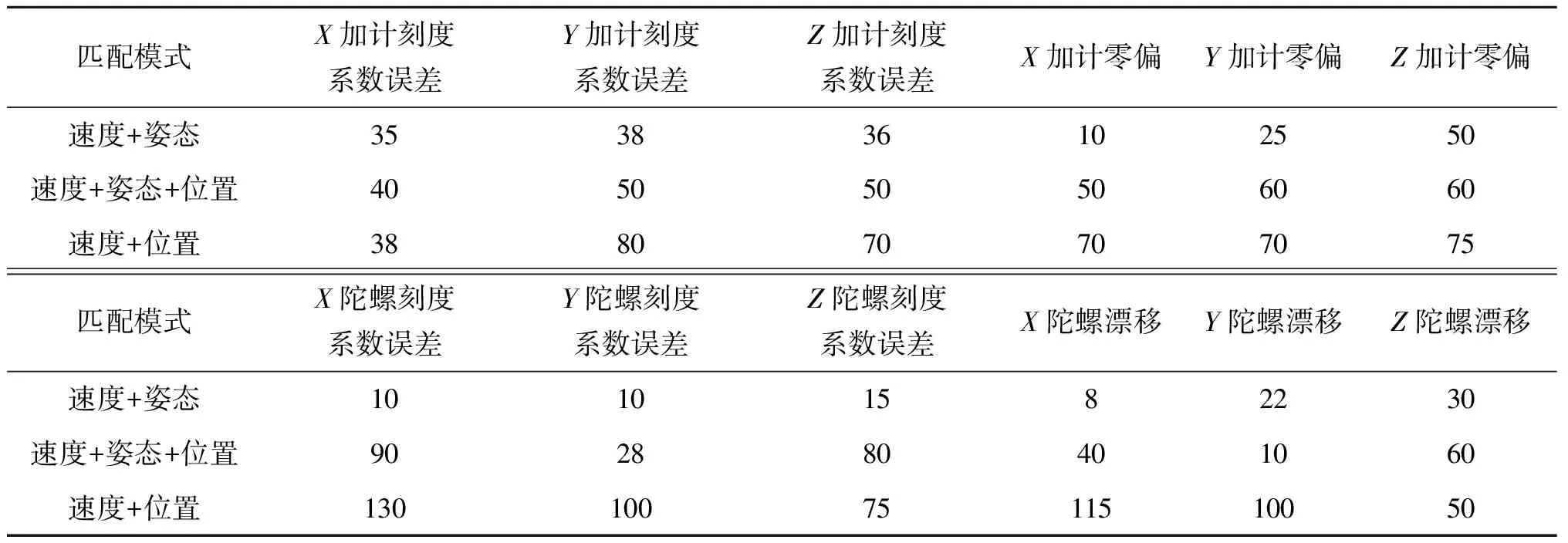
表4 不同匹配模式下各誤差參數收斂時間

由表3可以看出，對比速度加姿態匹配模式下各誤差參數的標定精度，采用速度加姿態加位置匹配時，Y軸、Z軸加速度計刻度系數誤差的標定精度有一定下降，而X軸加速度計刻度系數誤差、三軸加速度計零偏、X軸陀螺刻度系數誤差及Y軸、Z軸陀螺漂移等7個誤差參數的標定精度都有提高；采用速度加位置匹配模式時，X軸加速度計零偏和Y軸、Z軸加速度計刻度系數誤差的標定精度有一定提高，其余9個誤差參數的標定精度都明顯降低，其中Y軸、Z軸加速度計零偏及X軸陀螺刻度系數誤差的標定精度最差。

由表4可以看出，與速度加姿態匹配相比，增加位置觀測量后各誤差參數的收斂時間普遍增加，尤其是X軸、Z軸陀螺刻度系數誤差、X軸陀螺漂移和Y軸加速度計零偏的收斂時間增大明顯。這是由于增加了觀測量導致系統維數增加，必然導致計算量加大從而需要更長的解算時間；而速度加位置匹配相比速度加姿態匹配，除了X軸加速度計刻度系數誤差之外，其余誤差參數的標定時間都比較長，說明單純采用速度加位置匹配模式的在線標定效果一般。

綜上所述，采用速度加姿態匹配時，慣導12個誤差參數的標定效果較好；采用速度加姿態加位置匹配時，誤差參數的收斂精度有一定提高，但收斂時間較長；采用速度加位置匹配時，各誤差參數的標定效果較差。因此，在選擇匹配模式時要根據實際應用對標定效率及標定精度的要求，做到合理取舍。本文研究的誤差標定是以弾載捷聯慣導系統為應用背景，結合火箭炮工作實際，綜合考慮標定精度及標定效率，選取速度加姿態匹配模式標定效果最好。

4 結論

本文提出了一種新的可觀測度分析方法，該方法從系統初始誤差衰減的角度定義了系統狀態的可觀測性，能夠定量得到每一個狀態參數的可觀測度。同時推導了“速度+姿態”、“速度+姿態+位置”、“速度+位置”三種匹配模式下捷聯慣導系統的在線標定模型，并采用所提可觀測度分析方法對三匹配模式下各狀態量的可觀測度進行了定量分析。仿真試驗結果表明，本文提出的可觀測度分析方法是正確有效的，能夠對濾波估計效果進行預測，且通過對不同匹配模式下系統在線標定的估計精度和收斂時間進行對比分析，得出在捷聯慣導在線標定中選取“速度+姿態”匹配效果最好，對慣導系統在線標定方案優化有一定借鑒意義。