習題講評如何講出新意、評出深度
——以一元一次方程的習題講評為例

☉江蘇省蘇州工業園區星洋學校 周嬋娟

在當前教學生態下，數學課上的習題講評幾乎每節課都會涉及，離開習題的數學課堂幾乎是不可能的．而我們看到更多的是教師對習題的思路進行講解，或對學生進行思路上的引導，“評”的環節是一個薄弱點，這應該是我們教研的用力之處．本文先整理近期在聽一位年輕教師執教的一元一次方程習題課時的所見、所聞及課后筆者的簡要評課意見，供研討．希望借此話題引發大家對習題課講評時如何評出新意和深度有所啟發．

一、一元一次方程習題課聽課記錄與隨感

去分母，得15x-5x+5-1+3x+9=15.

移項，得15x-5x+3x=15-5+1-9.

合并同類項，得17x=2.

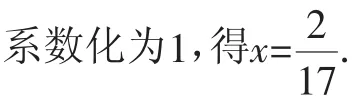
上述解法中有錯誤，教師先安排另一名學生上臺批改、查錯，學生找了一會兒發現上述解法在“去分母”一步中，對于方程左邊不含分母的項“1”漏乘，進而導致后續運算、求解出錯．

【聽課記錄】學生上臺板演如下：

解：分別解兩個關于x的一元一次方程，得：

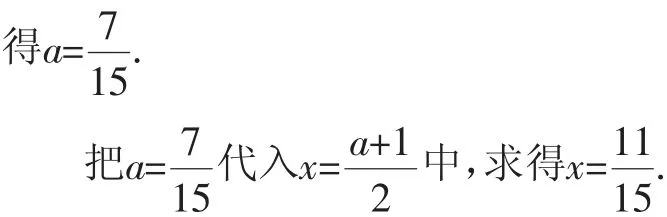
教師對學生的解法予以肯定．統計其他學生完成情況，發現只有一半左右的學生做出來，然后讓學生記錄整理，再講解下一題．

題3：當k為何值時，關于x的方程5x-2（kx-1）=24與方程3（x-1）+8=2x+3的解相同？

【聽課記錄】學生上臺板演如下：

列出這個方程后，學生發現不會解，但憑著對除法運算的理解，直接寫出k=8．

教師對答案表示了肯定，核對其他學生完成情況，發現多數學生都是正確的，就進入下一題的講評環節．

……

根據觀察得到的規律，寫出其中解是x=6的方程：_______________.

二、習題講評課要重視“評”的環節

1.訂正講評從糾錯走向究錯重視“治未病”

習題講評課要倡導“讓學”，具體的形式有讓學生上臺板演，讓學生參與批改，讓學生講解思路，讓學生參與評析，等等．“讓學”就能暴露學生的問題，然后開展糾錯、究錯與化錯教學．從上文4個題例的解題教學來看，執教者有很好的“讓學”理念與做法，題1就是“讓學”后學生的板演錯誤，然后另一個學生參與批閱，修正了錯誤．但是，我們認為，就這道方程習題的解法來說，與簡單訂正、修補錯漏相比，教師更需要進行現場“診評”，要診斷、評估學生出錯的根本原因是解法還需要優化，從解法開始兩步就需要進行優化、改進，以避免后續解法陷入繁難境地．以下是筆者給出的訂正與講評意見：

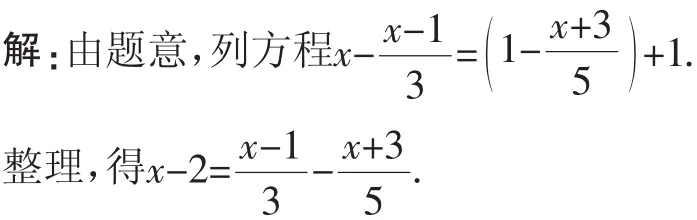
去分母，得15（x-2）=5（x-1）-3（x＋3）.

去括號，得15x-30=5x-5-3x-9.

移項，合并，得13x=16.

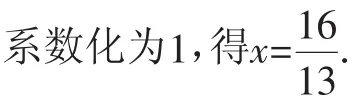
說明：上述“訂正”解法主要是前兩步，“列方程”與“整理”的步驟改進為后續去分母提供了較好的求解基礎．要向學生傳遞這種“防治未病”的解題理念，而不只是陷入繁雜之后再進行糾錯、修補．

2.多參數問題引導學生學會恰當消參策略

進入初中，從一元一次方程的學習開始，學生就會遇到很多含參數的代數習題，這類問題隨著年級的增加，會越來越多，不少學生顯得適應性不好．所以在七年級剛碰到這類含參問題時，就要向學生傳遞處理這類含參數問題的通用策略：消參．事實上，這與七年級下學期學習二元一次方程的“消元”思想是一致的．基于以上認識，上文“題2”“題3”的講評就有進一步優化的必要．

我們還可以著眼于第一個方程的a=2x-1，然后代入第二個方程實現消去a的目的，可以轉化為關于x的方程，實現思路貫通．要引導學生體會對比不同消參策略對于同一個問題求解繁簡的影響，增加他們解題路徑的智慧與優化的選擇．

3.講評規律探究問題，重視從特殊走向一般

規律探究是七年級有理數、整式加減中的高頻問題，雖然不是教材上的教學重點，但是在相關練習冊、月考、期中考試中都會碰到，在一元一次方程中規律探究問題不是很多，上面“題4”是一道好題．僅僅作為一道填空題進行訓練，還不足以發揮它的習題價值，以下對該題進行變式改編，打磨成一道功能更大的解答題：

“題4”改編題：

（1）解下列方程：

命題意圖：先安排學生從“特殊”出發，在解4個方程中觀察并發現規律，然后直接寫出后面兩個方程的解，第（3）問就是小結這類形式結構的方程的“通解”；第（4）問進行了包裝拓展，學生需要整理、變形為第（3）問的“一般形式”才能獲得有利解釋，對理解新歸納的“方程結構”提出了較高的要求，解法突出體現了從“非標準形式”向“標準形式”整理、變形、轉化的技能，是后續學習，特別是高中階段代數學習的關鍵能力．

三、寫在后面

教學即研究，筆者也見到不少高大上的“省、市”規劃課題，坦率地講，有些研究的內容實在是假、大、空，而“接地氣”的課例實踐與習題講評研究似乎不登大雅之堂，然而我們一線教師“年復一年”“日復一日”地做著“西西弗斯”推石上山、下山的事，能否在這個過程中運用研究的眼光，把習題教學講出新意、評出深度，本文只是結合一節課例中的題例講評闡釋了一些個性化的認識，不當之處，期待批判、爭鳴．