立足教材，全面構思，注重導向
——命制一道中考模擬壓軸題的心路歷程

☉重慶市萬盛經開區教師進修學校 猶廣江

中考是義務教育階段的終結性考試，重慶市中考數學試卷兼具“初中畢業生學業水平考試”和“高中招生考試”的功能.縱觀重慶歷年中考數學試卷，命題者在重視“四基”和核心素養的前提下，本著“穩中求變”的原則，試卷結構和考查重點具有相對穩定的風格.為了讓一線教師的復習有一定方向，適度減輕師生復習的負擔，根據《重慶市2018年初中畢業學業暨高中招生考試考試說明》，我區命制了相應的模擬試題.下面，筆者將其中壓軸題的命制過程記錄下來，與同行分享.

一、試題呈現

（1）求點A、B、C的坐標.

（2）如圖1，點P為直線BC上方拋物線上的動點，點M為拋物線對稱軸上的動點，MN⊥y軸，垂足為N，當△PBC的面積最大時，求PM＋MN＋BN的最小值.

（3）如圖2，平移拋物線，使頂點D在射線AD上移動，點D、A平移后的對應點分別為D′、A′.將△AOC繞點O順時針旋轉至△A1OC1，點A1恰好落在AC上，連接C1D′、C1A′，△A′C1D′能否為等腰三角形？若能，直接寫出點D′的坐標；若不能，請說明理由.

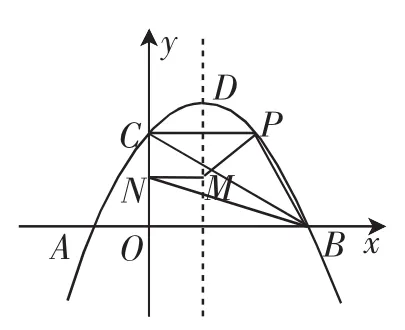
圖1

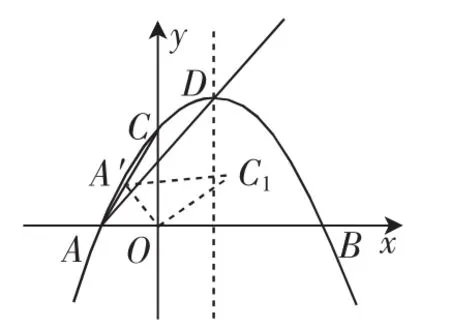
圖2

二、命題過程

按重慶中考試題的傳統風格，近年來壓軸題均為二次函數與幾何基本圖形相結合，側重考查學生的推理與探索能力的綜合題，通常設置三小問，起點較低，難度逐步上升，有明顯的層次性，充分體現了2011版新課標“不同的人在數學上得到不同的發展”的精神.考慮到第（1）問是基礎，為后面兩問提供必要而準確的條件，最初設想是確定二次函數的解析式，這樣既可關注學生對基礎知識的掌握程度，也能體現對二次函數重點知識的考查.但“根據不共線三點的坐標確定二次函數的解析式”在新課標中屬選學內容，故需告知一個常數，根據兩個點的坐標確定二次函數的解析式，只需解二元一次方程組即可得到解決.想到第（2）問需求直線的解析式，與此雷同，為避免考點重復，以覆蓋更多知識點，決定先給出解析式，求出拋物線上關鍵點的坐標.

（1）求點A、B、D的坐標.

分析：可通過拋物線頂點坐標公式或利用配方法求得D點的坐標；令y=0后解一元二次方程求得點A、B的坐標，考查內容均為核心知識，系數也較簡單，而且第（3）問中的△AOC也是一個“勾三股四弦五”的特殊直角三角形，便于學生后續思考.但通過計算發現，在第（3）問設計幾何變換時，不管將拋物線沿x軸方向，還是y軸方向，抑或沿射線AD方向平移，計算均較為復雜，數據較大，只好重新思考，加以改動.由試算過程發現，第（3）問計算復雜的原因之一是△AOC旋轉后，落點A1和C1的坐標關系不夠明顯，進一步想到如果∠CAO=60°，則點A1落在AC上時，A1C1∥x軸，點A1和C1的坐標關系顯而易見，故將點A、C分別調整為（，0）、（0，3），進而函數（3）問中有的點的坐標計算數據仍然太大.為保持圖形結構和設計思路不變，同時減小計算量，再次將點A、C分別調整為（-1，0）、（0，，進而函數解析式調整為了.但考慮到此時系數較復雜，故將函數解析式設計為頂點式，則學生不管是求頂點坐標還是解一元二次方程，均回避了復雜計算，降低了第（1）問的起點，由于頂點已在解析式中明確給出，求頂點坐標價值不大，故將求點D的坐標改為求點C的坐標.最終將總題干及第（1）問確定下來.

作為壓軸題，起點低是為了讓更多學生能動筆，不至于“望題生畏”，但同時要體現一定的區分度，讓學有余力的學生有充分發揮的空間.故第（2）問設置了兩個典型的最值問題相結合的綜合問題.一個是利用二次函數的頂點求三角形面積的最值，另一個是利用軸對稱求最短路徑問題.考慮到雙最值問題在近年重慶中考中已基本成為體現地域特色的傳統題目，如果僅僅是單純的“將軍飲馬”問題，學生會因應試訓練而形成套路，難免有死記硬背之嫌，思維含量相對會降低，試題的評價功能和補漏作用相對弱化，故在設計試題時適當增大了難度，在“胡不歸”問題和平移兩個命題方向上作了一定的選擇.考慮到“胡不歸”問題要利用三角函數構造直角三角形，含有比例關系轉換，難度相對較大，而平移涉及知識相對較少，且主要是線段的等量轉換，相對容易一些，故最后確定為考查平移變換.于是，第（2）問確定下來.

分析：在第（2）問的解決中，求△PBC面積的最大值時，涉及用待定系數法求直線的解析式、三角形面積計算、二次函數最值確定等多個核心知識點，在此基礎上求線段和的最小值時，由于MN為定長，故需先將點P向左平移距離|MN|，再構建“將軍飲馬”模型，利用勾股定理求出PM＋BN的最小值.這樣設計，試圖讓學生經歷一系列觀察、猜想、探究和發現，并通過必要的計算和推理，考查學生綜合運用知識分析問題、解決問題的能力，同時體現了對學生數學運算、邏輯推理、數學建模等核心素養的考查.

作為重慶中考數學試卷的最后一道試題，其層次性和區分度充分體現了重慶中考畢業和升學的雙重功能.第（1）問絕大部分學生能動筆，重在學業水平考試，第（2）問設置了兩個層次，求△PBC面積的最大值，重點考查中等以上學生的基本能力，求線段和的最值，對優秀學生的思維能力提出了較高要求.而作為壓軸題的最后一問，其作用更多的是給特優生發揮的空間.故在設計動態幾何的探究問題時，設計了三角形的旋轉和拋物線的平移兩個幾何變換，同時，結合等腰三角形設計了點的存在性探索問題.

分析：在第（3）問中，△AOC的旋轉考查特殊直角三角形及等邊三角形的相關知識，而平移拋物線，則要求學生關注運動過程中的不變量，利用解析法表達線段長度，進而根據等腰三角形的定義列方程求出相應點的坐標，這一過程還考查學生分類討論的數學思想方法.第（3）問的解決不僅對學生的思維能力和空間想象能力有較高要求，對運算能力的要求也較高.在第（1）問的設計時充分考慮問題間的延續性，精心設計數據，便于第（3）問的解決，同時考慮到整個試題的復雜程度及其在試卷中的定位，故設計為直接寫出點D′的坐標，而無需寫出解答過程.在平移的方向選擇上，最初設想是沿坐標軸平移，點的坐標關系會明確一些，但經過反復試算比較，發現不管是沿x軸還是y軸平移，都存在計算復雜，且數據都較大的問題，而沿射線AD方向平移，計算量相對較小.至此，第（3）問也最終確定下來.

三、命題感悟

1.試題命制需全面構思，反復打磨

原創試題對命題者要求較高，平時需深入學習課標，理解教材，研究考試，熟悉經典題型，研討經典解法，大量積累才會有源頭活水；命題過程中的思考和探究，只有反復打磨，才能精益求精，才能在繼承傳統的同時又有新的突破.回顧此題的命制，從考點的選取，到數據的確定，無不經歷了反復思量、仔細推敲的過程，既要考慮每一小問的評價定位，又要考慮各問之間的延續性.如第一問的設定，既要保證其基礎性，又要充分考慮到第（2）問和第（3）問的解決，必須系統進行思考，故第（1）問確定了，此題便已成一半.

2.好的試題要有導向教學的作用

（1）立足教材.

本題的問題設計試圖引導一線教師在教學和復習中要立足教材.第（1）問給出拋物線的頂點式方程，求其與坐標軸的交點坐標，難度小，容易入手，旨在讓學生從熟悉的課本知識開始問題的解決；第（2）問中的雙最值問題，把初三二次函數的最值用于求幾何最值，與八年級的綜合實踐內容“將軍飲馬”合二為一，可謂“源于教材，而又高于教材”.

（2）把握中考方向.

中考命題具有考查學生知識與能力及教學導向雙重功能.而作為中考模擬題，還有引導師生復習復習的作用，力爭提高復習效率.筆者認真學習《重慶市2018年初中畢業學業暨高中招生考試考試說明》，深入鉆研重慶歷年中考試題，以二次函數和基本圖形為載體，考查基本圖形的性質及圖形的運動變換等重要知識點，其考點的選擇、試題的綜合性，對教師把握壓軸題的復習方向起到了很好的導向作用.事實證明，這道模擬題與最終的中考題有較高的相似度.

（3）關注數學思想方法和核心素養.

本題的命制關注了學生對數學思 想方法的感悟.不管是第（1）問中求點A、B的坐標，還是第（3）問中點D′坐標的確定，都體現了方程思想；而第（2）問中構建二次函數求△PBC面積的最值則是函數思想的很好體現；以幾何和函數為背景的綜合題，其結合點則是數形結合；第（3）問中等腰三角形存在性的探索則是對分類討論思想的考查.數學思想與數學學科核心素養一脈相承，重視數學思想方法是提高學生核心素養的有效途徑.本題突出了對學生直觀想象、數學運算、邏輯推理、數學建模等核心素養的考查，也希望通過試題向教師傳遞關注數學思想方法和核心素養的教學主張.