在聽、評課中發展“現場學習力”
——以“二次根式”起始課聽課、評課為例

☉江蘇省南京外國語學校 吳凱紅

華東師大博士生導師李政濤教授對教師的“現場學習力”有如下論述：良好的現場學習力需要專注其中，即無論是面對自己的課堂、同行課堂或是教研活動，不同的人往往有不同的收獲.最近參加一次市級教研活動，觀摩學習了一節“二次根式”起始課，不但課上得精彩，而且課后的評課意見也很受教益，現整理出來，并提出自己的一些學習心得，與有興趣的同行共享.

一、“二次根式”起始課教學整理

教學環節（一） 回顧舊知，引出新知

問題1：4、16、（-4）2、0、2、a的平方根、算術平方根分別是多少？

教學預設：學生回答之后，教師講授二次根式的描述性定義，形如a≥0）的式子稱為二次根式“，”稱為二次根號.

接著給出兩組練習（略），一組訓練如何識別二次根式，追問學生是如何判斷的，另一組主要訓練被開方式的意義問題.

課堂片段：

師：這節課我們從數的算術平方根說起，4的算術平方根是什么？（等待）

生1：因為2的平方等于4，所以4的算術平方根為2.

其他學生幾乎不會，等待了將近1分鐘學生還是沒有反應.

師：我們一起回顧一下算術平方根吧！我們學習數學就是要表達自己的熱情，你們忘了嗎？小組一起回顧一下吧！腦子里還沒有印象的請舉手.

師：16的算術平方根是什么？

師：非常棒！

師：0的算術平方根是什么？

學生繼續回答：2的算術平方根是______，a的算術平方根是______.

自主練習：下列式子哪些是二次根式？你是如何判斷的？

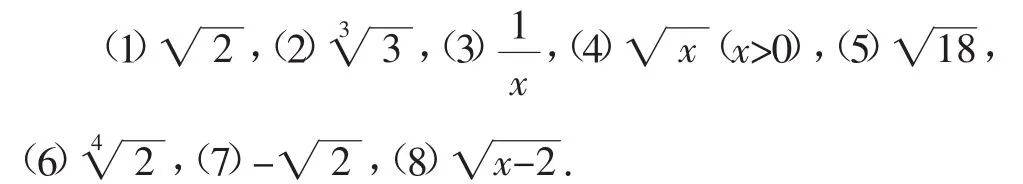
教學環節（二） 從定義出發，探究性質

教學預設：引導學生理解算理，回到定義來說理，即根據乘方與開方運算的互逆關系，可得（）2=a（a≥0）.

教學預設：引導學生理解算理，回到定義來說理，即根據乘方與開方運算的互逆關系，可得=|a|.如果學生忽略a也可取負值，則安排學生充分討論，舉出不同數來驗證、確認.

教學環節（三） 性質運用，化簡計算

題組2：下列二次根式有意義時，分析x的取值范圍.

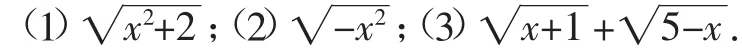
教學環節（四） 反思小結，完善板書

小結問題：同學們是如何理解二次根式的定義的？

在本課中是如何得到二次根式的性質的？

完善板書如下：

二、評課意見摘選

評課老師1：這節課從溫故知新開始，充分等待學生，抓知識的生長點——算術平方根，體現了客從何處來的理性追問精神；回歸定義，善于捕捉課堂生成，緊抓新知生長點；關于二次根式性質探究，緊扣代數學習的套路，從定義到性質再到運算，整個過程順暢、自然；對于本課重、難點，在課堂小結時做得細致到位，而且有一個漂亮的板書.可以說，這節課不僅讓學生學習到了二次根式的相關知識，還讓學生積累了從特殊到一般和從抽象到具體的數學思想.

評課老師2：在不斷的追問中體現教師的主導性，又體現著學生的主體性；在自主練習中凸顯相關的性質；在小結概括中知二次根式全貌，能讓學生知其然并知其所以然，自始至終強調學生怎么想的.在課堂小結時，不落俗套.教師設計了兩個問題：你是如何理解二次根式的定義的？如何得到二次根式的性質的？通過二次根式概念和性質的學習，你積累了哪些學習方法和經驗？關于本節課上小組活動的處理方式，有猜想時看似教師完全放手，讓學生學會學習，讓學生歸納總結，又沒有完全放手，在小組合作的部分給出了要求，放和收做得自如.關于定義，有一個疑惑，提出來與大家一起思考：根據定義，形如（a≥0）的式子稱為二次根式，那么根據定義，3是不是二次根式？-是不是二次根式？

評課老師3：這節課中，教師對二次根式有深刻的理解，從帶根號的算術平方根出發，從特殊值代入并探討到總結一般性的規律，通過算術平方根定義驗證，注重知識課堂的生長.教師給學生充分留白，靜靜地等待學生的回答，對于性質的處理，學生的回答不對，教師一個小問題的引導，利用（）2=4，（）2=a，提問學生是否還有其他方法來驗證.探討性質時，一步步引導學生驗證方法，走套路.對于性質3的證明，充分利用李庾南老師倡導的自學·議論·引導，現學現賣.對于2個性質異同的理解（與（）2），從學生對于性質的把握看應該掌握了.

評課老師4：概括起來，用以下幾個關鍵詞來評這節課，就是展示多、結構佳、思維深、創意好.具體來說：

（1）展示多.執教老師在課堂上讓學生說，說結果，在白板上寫出來到前面展示.充分將思維誤區展示，讓學生自己發現錯誤并糾正，教學過程中注重抓取學生錯誤，是化錯教學.

（2）結構佳.板書非常棒，體現了結構化板書的特點.

（3）思維深.開課由定義出發，從算術平方根走向二次根式，在課堂上滲透了從具體到抽象、從特殊到一般的數學思想方法.很好地培養了學生的思維能力，通過不斷追問，讓學生聯想到原生態的算術平方根的意義，通過追問，讓學生的知識點得到生長.

（4）創意好.體現“學材再建構”，重組了教材，凸顯了常見的數學思想方法：類比、從特殊到一般的數學思想方法.

三、進一步的思考

1.深刻理解教學內容，從定義出發

課堂教學要求應“標”而定，即對照課標，學習知識開始時要簡單，如中國古代山水畫卷一樣漸次展開.二次根式的知識生長點在算術平方根，所以選擇從算術平方根出發定義二次根式并依據定義探究歸納二次根式的性質，這個過程看似慢、低效，實質上是向學生滲透“回到定義”去研究的學習方法.事實上，不只是新知探究要堅持“從定義出發”，解題教學更需要向學生傳遞“回到定義”的解題思想.比如，上文評課老師2提出的問題是不是二次根式？-是不是二次根式”，我們仍然應該回到定義來思考這個疑惑.二次根式的定義是“形如（a≥0）的式子稱為二次根式”，根據定義一定是二次根式，但是3是一個二次根與3的積，在辨析二次根式時應該回避這類問題，教師本人不應該糾結，若糾結說明教師對描述性定義 沒有達到深刻理解.

2.內容簡單的課如何“教活”“教深”

有人說，“二次根式”起始課內容簡單，沒有什么好講的，二次根式的性質也是顯而易見的，沒有什么好講的，上面的課例是不是內容太少、容量不夠？這是當前很多習題單式導學案的通病.教師對概念教學的認識不夠，往往對內容簡單的課通過加大題量來應對教學時間，這是得不償失的.我們認為，對于二次根式的性質，不能簡單“一帶而過”，而應該與學生一起討論、舉例驗證，作必要的推理演算，即從特殊數入手到一般推導再證明.在上面的課例中，至少體現了兩種數學思想方法，即向學生滲透從特殊到一般、從具體到抽象的數學思想方法.