相干時間超過10 min的單離子量子比特*

汪野 張靜寧 金奇奐

(清華大學交叉信息研究院量子信息中心, 北京 100084)

(2018 年 9 月 19 日收到; 2018 年 10 月 18 日收到修改稿)

能夠長時間儲存量子信息的量子存儲設備是實現大規模量子計算和量子通信的基本要素. 與其他量子計算平臺相比, 囚禁離子系統的優勢之一在于具有很長的相干時間. 此前, 基于囚禁離子的單量子比特相干時間不到1 min. 研究發現, 在囚禁離子系統中, 限制量子比特相干時間的主要因素是運動能級加熱和環境噪聲, 其中后者包含環境磁場漲落和微波相位噪聲. 在同時囚禁171Yb+離子和138Ba+離子的混合囚禁系統中, 通過實施協同冷卻和動力學解耦, 可以實現相干時間超過10 min的單離子量子比特. 這一技術有望用于實現量子密碼學和搭建混合量子計算平臺.

1 引 言

量子計算和量子模擬[1]是近年來飛速發展的理論與實驗并重的熱點研究領域之一. 它以量子力學和量子信息學為理論基礎, 以囚禁離子、超導電路等實驗技術的進步為前提, 致力于實現實用的量子計算和量子通信[2,3], 具有廣闊的應用前景. 量子計算平臺的基本元素是量子比特, 它是完全可控的量子二能級系統, 人們可以對其進行初始化、量子邏輯門和測量等基本操作. 量子力學中的不可克隆原理告訴我們, 儲存在量子比特上的未知量子信息不能被精確地復制[4,5]. 這項量子信息獨有的性質只能夠通過對單個量子比特的相干操作和探測來驗證. 如果不能完全控制單個量子比特, 量子信息的儲存、操作和讀出從根本上是難以令人信服的. 長期以來, 人們一直致力于發展在單量子比特層面的相干操作和探測技術.

囚禁離子量子比特的長相干時間將成為實際量子計算和量子通信的基本元素之一. 囚禁離子系統是實現大規模量子計算機的領先物理平臺之一.利用離子阱技術構建大規模量子網絡的規模化方案[6]包括光子鏈接[3]和離子穿梭[7]. 光子鏈接方案結合了遠程量子通信和局域量子計算, 為實現量子網絡提供了一個競爭性很強的物理平臺. 人們已經演示了離子光子糾纏[8]以及以光子為媒介的遠距離離子糾纏[9], 這是構建離子-光子網絡的基本單元. 離子穿梭方案是將囚禁離子系統劃分為操作區域和存儲區域, 通過離子穿梭技術在區域間移動離子.在這一架構下, 人們已通過實驗演示了操作區域的基本結構和操作[10]. 隨著系統規模的增大, 對存儲區域量子比特儲存時間的需求將相應增加. 為了將量子比特誤碼率保持在容錯量子計算的閾值之下,延長量子比特的相干時間是十分關鍵的. 隨著系統規模的增大, 這兩種方案對量子比特的相干時間的要求都會相應地提高.

二十多年前, 人們在離子系綜里利用磁場不敏感的內態實現了大約10 min的相干時間[11,12]. 然而, 經過十多年的發展后, 單量子比特系統的相干時間仍然遠低于系綜相干時間, 只有不到1 min[13?15]. 對于囚禁離子量子比特, 特別是基于超精細能級的量子比特, 由自發輻射導致的固有弛豫時間T1遠長于由磁場漲落和本振源的相位噪聲導致的退相干時間T2*. 目前在離子阱系統中限制相干時間的主要是環境磁場漲落和本振源相位噪聲導致的非相干演化, 同時我們還注意到, 加熱導致的測量效率降低也極大地限制了離子阱系統中相干時間的測量[16,17]. 具體來說, 由于運動能級加熱, 離子的波包隨時間不斷彌散, 收集到的熒光光子數減少, 這使得區分離子內態的測量效率低下.在硬件方面, 通過清潔離子阱表面[18]或將離子阱置入低溫環境中[19]可以顯著地抑制運動能級加熱效應. 在同時囚禁不同種類離子的混合囚禁系統中,還可以通過協同冷卻來消除運動能級加熱, 從而保證在整個實驗過程中探測效率不降低. 此外, 動力學解耦技術能夠消除來自環境磁場和本振源的噪聲, 從而延長量子系統的相干時間[20?22]. 最近有文獻報道, 在離子化供體的核自旋系綜中實現了小時量級的相干時間[23,24].

2 協同冷卻

令人奇怪的是, 二十年前關于離子系綜的實驗中[11,12]測得的相干時間遠比在最近的單離子實驗中測得的相干時間來得長, 前者大約是10 min, 而后者最長不超過1 min[13?15]. 現在已弄清了導致這一現象的原因. 原因之一是能夠操作單量子比特的離子阱系統復雜度遠高于之前的離子阱系綜系統,導致很難在系統上實施磁屏蔽以降低磁場噪聲; 原因之二是離子阱系統的背景加熱使得同種離子的探測效率隨著時間的增加而大量降低. 之前離子阱系綜的系統使用了非常大型的離子阱結構, 這種結構的電極與離子云距離較遠, 背景加熱較低. 但是為了能夠實現速度較為理想的量子比特門, 量子信息領域中使用的離子阱結構都更加微小, 導致背景加熱效應更加顯著. 因此我們相信, 只要找到合適的方法, 能夠在激光冷卻停止后減輕運動加熱效應, 單離子實驗應該可以展示出和離子系綜可比擬的長相干時間.

對光學性質不同的兩種離子的混合離子晶體執行協同冷卻操作可以壓制運動加熱效應, 同時不影響編碼在其中一種離子的內態上的量子比特中的量子信息的相干性. 在基于囚禁離子的量子信息領域典型的Paul離子阱中, 通過同時囚禁兩種類型的離子, 這里選擇的是171Yb+和138Ba+, 我們可以實施協同冷卻. 其中, 單個171Yb+離子作為量子比特, 單個138Ba+作為制冷離子.171Yb+離子具有的基態電子組態具有兩個磁場不敏感的超精細能級, 這使得編碼于其上的量子比特本身具有較長的內稟相干時間. 同時, 選用138Ba+離子是因為這兩種離子的質量相對接近, 使得協同冷卻效率更高.

2.1 實驗裝置

協同冷卻的原理是通過對一種離子施加冷卻激光, 從而冷卻由兩種離子組成的混合離子鏈的運動模式, 因此需要在離子阱中同時囚禁兩種類型的離子. 圖1(a)所示為一個標準的Paul離子阱同時囚禁了171Yb+離子和138Ba+離子. 圖中, 兩種離子所對應的操作激光均覆蓋整個離子鏈, 這是因為離子鏈中的離子會在熱噪聲的作用下交換位置. 同時, 由171Yb+離子和138Ba+離子的能級圖可知, 兩種離子的光學特性差異很大, 對138Ba+離子進行激光冷卻不會影響編碼在171Yb+離子上的量子比特的相干性.

171Yb+離子2S1/2電子組態的兩個超精細能級被定義為量子比特的兩個能級. 這兩個能級的特征頻率之差為 1 2642812118+310.8B2Hz, 其中B是以高斯為單位的磁場強度的數值. 在實驗中, 可以通過標準的光泵技術將量子比特制備到 |↓〉 態, 并通過熒光測量技術來區分量子比特的兩個能級.

圖1(b)是用于產生激光和微波信號的控制系統的示意圖. 其中微波信號由微波振蕩器的信號和直接數字合成器的信號混合而成, 并受到可編程邏輯門陣列的控制. 該控制系統能夠在 1 00 ns 內改變微波信號的相位. 所有微波源相位均以銣原子鐘為標準. 為了處理波長為369 nm的激光的泄漏問題,設計了由聲光調制器、電光脈沖選擇器和機械快門組成的三段開關. 該激光用于171Yb+離子的多普勒冷卻、熒光探測和光泵操作. 因為該激光頻率與量子比特的躍遷頻率接近, 稍有泄漏即會導致巨大的退相干效應.

2.2 冷卻效果

衡量協同冷卻效果的直接途徑是測量171Yb+離子在協同冷卻過程中達到的平衡態溫度. 為測量平衡態溫度, 需要利用雙光子拉曼躍遷來耦合內態與運動能級, 從而測量運動能級布居數分布. 然而,這需要在實驗系統中增加額外的激光和相應控制系統.

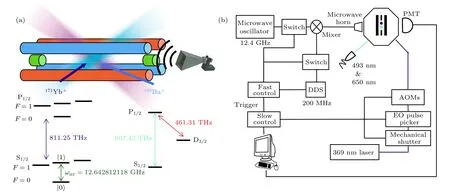
圖1 實驗裝置和控制系統 (a) 同時囚禁 1 71Yb+ 離子和 1 38Ba+ 離子的混合囚禁系統及相關能譜圖; (b) 微波和激光信號的控制系統Fig.1. Experimental setup and control system: (a) Hybrid trapping system that traps 1 71Yb+ and 1 38Ba+ simultaneously;(b) control system for generating laser and microwave signals.

另一方面, 協同冷卻的效果可以從離子鏈的穩定性來側面反映. 在協同冷卻的過程中觀測到, 兩個離子大約每5 min交換一次位置. 除此之外,離子從未自阱中逃逸, 甚至可以在阱中穩定存在超過一星期, 這使得超長相干時間的測量成為可能.

由于在實驗過程中離子的位置會交換, 保證離子鏈中兩個離子所處的環境完全一致是十分重要的, 比如熒光探測和光抽運的效率、磁場和微波場的強度等. 在不進行動力學解耦的情況下, 該系統中單量子比特相干時間大約為800 ms.

3 動力學解耦

在利用協同冷卻技術抑制了運動能級加熱效應后, 剩下的退相干的主要因素是磁場漲落和用于操作量子比特的微波的相位漲落, 它們將導致量子比特的相位隨機化. 利用動力學解耦技術, 可以抑制來自環境磁場漲落的外界噪聲和本振源的相位噪聲[20,25?29].

量子比特的演化由如下隨機哈密頓量決定,

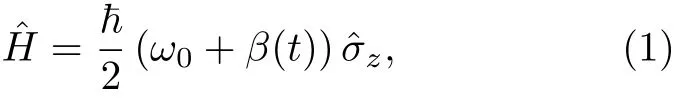
其中,σ?z是泡利自旋算符的z分量,ω0是兩個能級的頻率差,是隨機相位噪聲,βB和βLO分別代表環境磁場漲落和操作微波相位漲 落 的 影 響 .β(t) 滿 足〈β(t)〉=0 和

為延長量子系統的相干時間, 動力學解耦技術[30]在量子信息領域被廣泛應用, 是用來消除隨機相位噪聲影響的一項標準技術. 動力學解耦最簡單的實施方案是Hanh回波[31], 又被稱作自旋回波.在經過一段時間τ的退相干后, 該技術通過一個翻轉脈沖( π 脈沖)來實現自旋系統的重對焦, 從而在時間為 2τ時得到增強的回波信號. 然而, Hahn 回波無法消除時間尺度比τ更小的系統-環境相互作用擾動. 為解決這一問題, 人們試圖使用一系列等距 π 脈沖來消除高頻擾動, 即 Carr-Purcell (CP) 序列[32]和 Carr-Purcell-Meiboom-Gill (CPMG) 序列[33]. 可以形象地把這一類型的動力學解耦序列對系統的作用理解為將不需要的相位漲落通過時間平均的方式消除掉. 這類方案原則上要求 π 脈沖之間的間隔τ盡可能小, 然而在實際實驗中τ的取值受到硬件和系統最大可承受功率的限制.

另一方面, 人們也嘗試尋找利用有限數量的脈沖獲得最優性能的動力學解耦方案. 對純退相干的系統-環境相互作用, 動力學解耦序列可看做系統演化的濾波器, 濾波函數與環境噪聲譜的重疊決定了量子態的衰減率. 比如, 前述CPMG序列可看做帶寬為 2 π/τ的高通濾波器. 因此, 如果環境噪聲譜已知, 可以設計合適的濾波函數來得到最優的衰減率, 這就是基于非等距脈沖序列的動力學解耦方案[34]的核心思想.

此外, 動力學解耦序列的實際性能還受到脈沖誤差的限制. 在許多情況下, 脈沖誤差主要由系統誤差構成, 比如經典控制系統的校準誤差. 源自核磁共振系統的組合脈沖方法[35]可以將系統誤差減少到O(εn) , 其中ε是裸的系統誤差率. 完全補償的組合脈沖可以用于任意初態, 替換任意單個脈沖而不影響其他脈沖. 將組合脈沖與動力學解耦結合起來的方案是 KDD?方案[21], 其中下標?是 Knill組合脈沖[36]的參數, 決定了 π 脈沖在x-y平面上的角度.

由于動力學解耦方案的性能對噪音環境的特性敏感, 我們測量了系統的噪聲譜, 并據此為動力學解耦序列選擇合適的參數. 具體來說, 采用CPMG方案來測量系統噪聲譜, 采用 K DDxy方案來延長量子比特的相干時間, 圖2所示即CPMG方案及 K DDxy方案對應的脈沖序列.

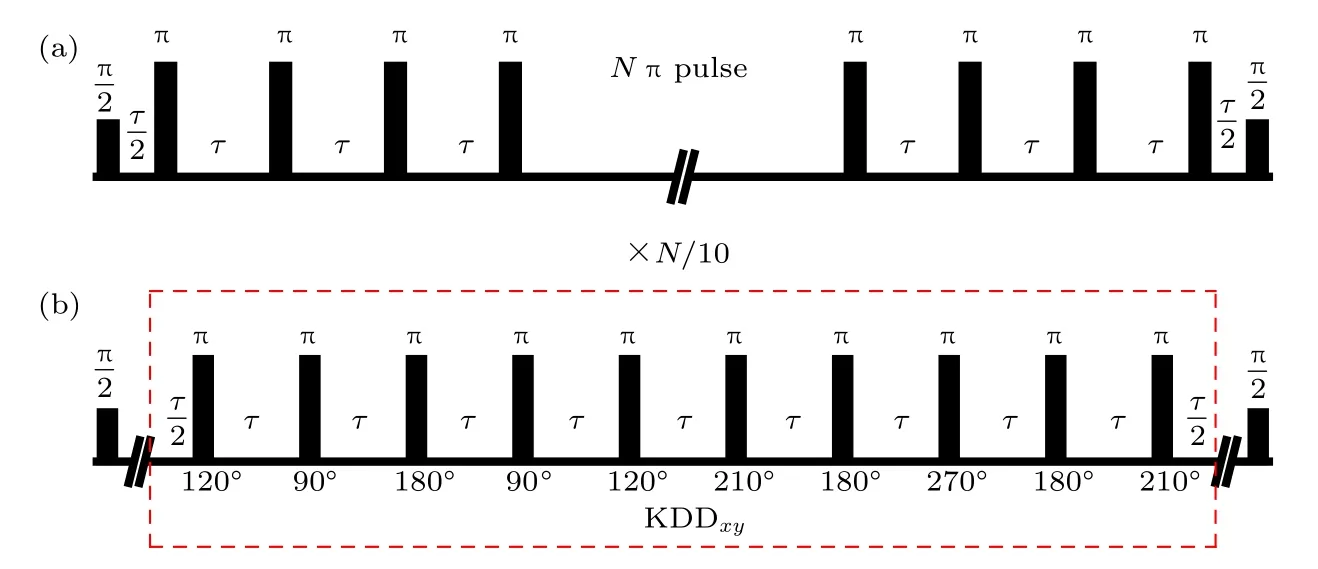
圖2 動力學解耦脈沖序列 (a) CPMG 方案; (b) K DDxy 方案Fig.2. Pulse sequence for dyanmical decoupling: (a) CPMG protocol; (b) K DDxy protocol.

3.1 濾波函數

為了刻畫動力學解耦序列對量子態演化的影響, 需要計算動力學解耦序列對應的濾波函數. 任意動力學解耦序列可以看作在T時間內執行n個π脈沖操作, 第i個 π 脈沖對應的方位角和時刻分別為?i和τi, 并約定

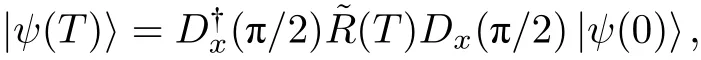
其中與動力學解耦序列和系統在噪聲環境中的演化對應的演化算符可寫為

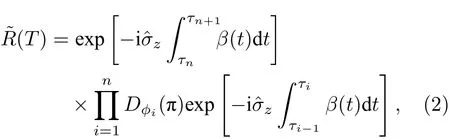
其中單量子比特旋轉

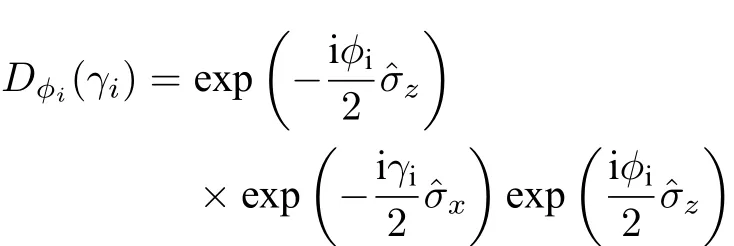
考慮到γi=π , 上述演化算符可化簡為

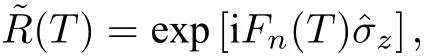
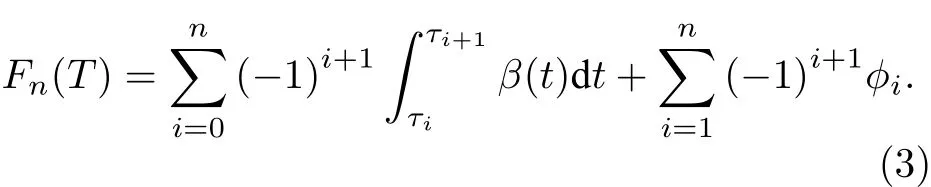
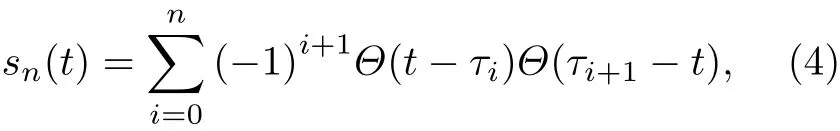
其中Θ(·) 是Heaviside階梯函數.

在拉姆齊條紋實驗中, 執行動力學解耦序列之后, 測量的信號是自旋算符z分量的期待值, 即

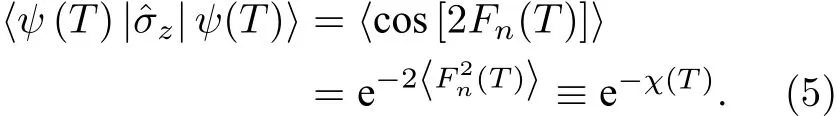
推導(5)式時, 使用了對高斯型隨機變量X成立的等式定 義時域濾波函數的傅里葉變換

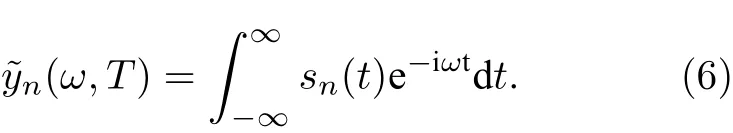
利用卷積定理, 信號的衰減函數χ(T) 可寫成如下形式:

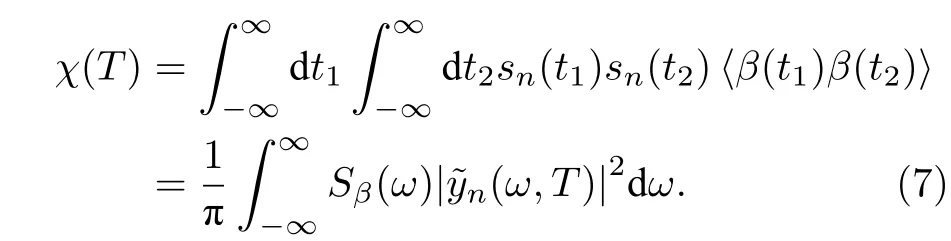
3.2 環境噪聲

如前所述, 系統的隨機相位噪聲β(t) 包含來自隨機磁場漲落和操作微波相位漲落兩方面的影響,分別用βB(t) 和βLO(t) 表示. 操作微波相位漲落βLO與本地振蕩器的品質有關, 在使用高品質本地振蕩器、銣原子鐘和直接數字合成器等設備后, 由頻譜分析儀測得的典型相位漲落如圖3所示.

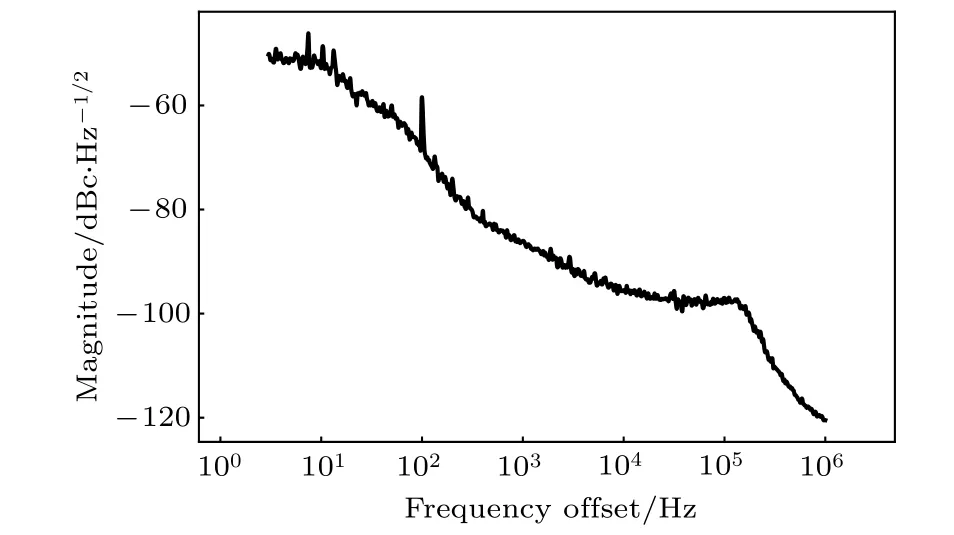
圖3 頻譜分析儀測得的典型相位漲落噪聲譜Fig.3. Typical phase noise measured by spectrum analyzer.

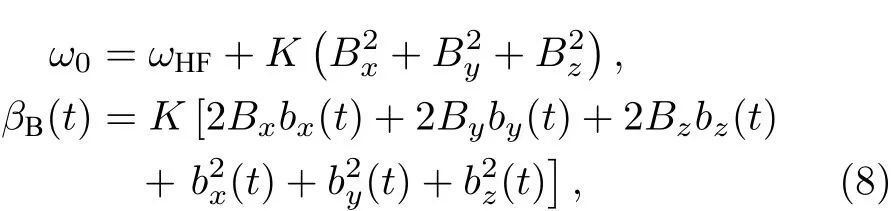
其中ωHF是超精細能級劈裂,Bi是磁場在i方向的平均值,bi(t) 是i方向的磁場漲落 假設降低磁場平均值不影響漲落的大小, 則可以通過減小磁場的方式來壓制βB(t) , 從而得到更長的相干時間. 由通量計測得因此使磁場沿x方向. 在研究系統噪聲譜時, 采用在實現長相干時間量子存儲時, 采用這是能夠對離子的內態進行有效熒光測量的最小磁場.

系統中最強的噪聲組分是來自于電源線的50 Hz振蕩及其諧波, 因此頻域噪聲譜可以用分立模型來模擬[37,38],其中δ(·)代表狄拉克δ函數. 將β?(ω) 代入 (5) 式, 得到最終 信號為

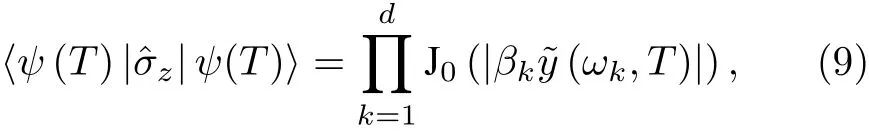
其中 J0(·) 是0階Bessel函數. 實驗上測得末態平均值的平均脈沖間距變化的數據后, 可通過數值擬合得到分立噪聲譜強度βk.

接著, 通過連續噪聲模型來進一步研究系統噪聲譜. 對任意噪聲譜拉姆齊條紋的對比度可表示為, 其中

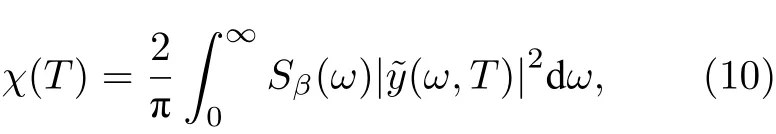
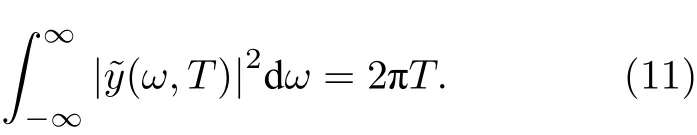
4 基于微波的量子門操作

量子比特躍遷可通過微波來驅動, 微波信號是通過混合來自安捷倫微波振蕩器的12.442812 GHz的信號和來自直接數字合成器的 2 00 MHz 的信號產生的. 經過一次放大, 微波信號通過放置在視窗附近的微波喇叭施加于系統. 由于動力學解耦序列通常包含數千乃至數萬個單比特邏輯門, 邏輯門誤差的累積會導致量子比特退相干. 因此, 微波驅動的單比特量子邏輯門的保真度是實現長相干時間量子存儲的最重要的因素之一.

4.1 隨機化基準測試

隨機化基準測試[39]是用來測量極低的單比特量子邏輯門的保真度的一種標準方法. 傳統上, 量子操作的誤差行為可以通過量子過程層析來標定.然而, 雖然量子過程層析可以提供關于量子操作的許多信息, 但卻無法保證該量子操作嵌入一長串其他量子操作中的表現. 另一方面, 規模化量子計算要求單個量子操作的誤差率在 1 0-4量級或更低.通過傳統的量子過程層析在實驗上測定這樣低的誤差率是很困難的. 此外, 量子過程層析無法排除初態制備和測量過程引入的誤差. 因此, 人們提出了一種可以克服以上問題的對量子操作的誤差行為進行實驗研究的新方法, 即隨機化基準方法.

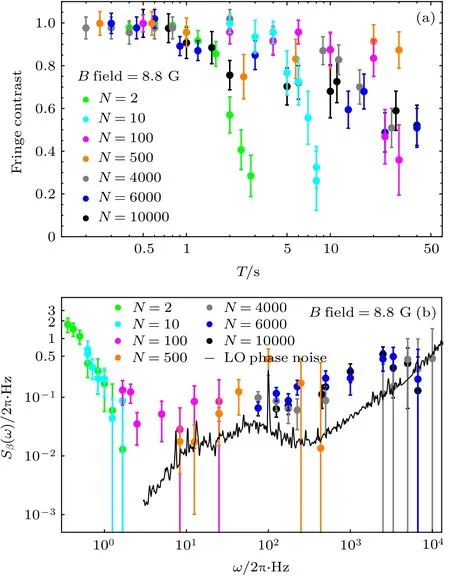
圖4 (a) 執行包含 N 個脈沖的動力學解耦序列, 不同的總演化時間 T 對應的條紋對比度; (b) 通過分析圖(a)中的數據得到的環境噪聲譜Fig.4. (a) Ramsey contrasts depending on the total evolution time T for various numbers of pulses N in the dynamical decoupling sequence; (b) the noise spectra analized from the measured data in Fig.(a).

隨機化方法最初是在量子噪聲領域提出的, 其具體過程是對系統實施隨機幺正操作及其逆操作假如噪聲模型可表示為施加在之間的獨立的量子操作, 保真度的下降程度即代表了系統的噪聲強度. 隨機化基準方法是隨機化方法的簡化版本, 表現在前者將隨機幺正操作限制為Clifford門操作.

隨機化基準方法對標準初態執行不同長度的隨機的量子邏輯門序列, 每一序列均以隨機化測量結束, 該測量決定系統是否達到正確的末態. 根據最終測量的錯誤率隨序列長度的增加可以確定序列中每一個門操作平均的計算相干的誤差率. 序列中的隨機門操作出自Clifford群, 該群是用e-iσπ/4的 π /2 旋轉生成的, 其中σ是作用于不同量子比特的泡利算符的直積.

對于單量子比特系統, 隨機化基準方法包含大量實驗, 每一實驗的流程均包含初態制備、執行不同的量子邏輯門序列和測量, 其中量子邏輯門序列包含泡利隨機化和門計算兩部分. 泡利隨機化執行具有形式的幺正操作, 其中隨機變量是恒等算符. 門計算執行形式為的幺正操作,u∈{x,y}. 除了最后一個 π /2 脈沖, 上述符號、隨機變量b和μ都由均勻隨機采樣得到. 選擇系統初態為|0〉, 是由于序列中的操作均出自Clifford 群, 理想情況下系統的狀態總是泡利算符的本征態. 最后一個 π /2 脈沖將系統狀態旋轉為的本征態, 最終測量是關于的馮諾依曼測量. 在理想情況下, 最終測量的結果是已知的. 在誤差環境下, 由于隨機化, 序列的誤差與組成序列的單個或數個操作無關. 序列的長度l是序列中 π /2 脈沖的個數. 可以測量不同長度l的序列對應的誤差率pl, 由pl與l的關系可以估算門脈沖的平均誤差率,

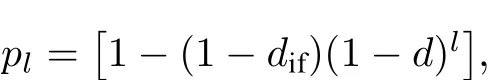
其中d是隨機化計算門(一個 π /2 脈沖和一個泡利脈沖的隨機組合)的平均誤差率,dif為包含初態制備和測量過程的誤差率.

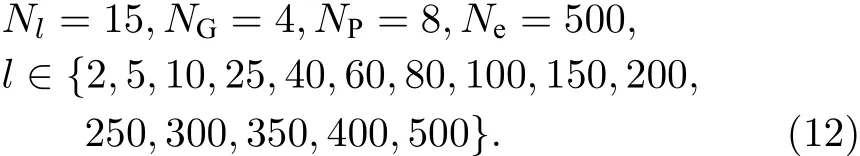
圖5展示了不同序列的保真度, 對于序列長度l的每一個不同取值都存在32個數據點, 由此可以估算單量子比特邏輯門保真度為99.994%±0.002%.

5 測量單量子比特相干時間

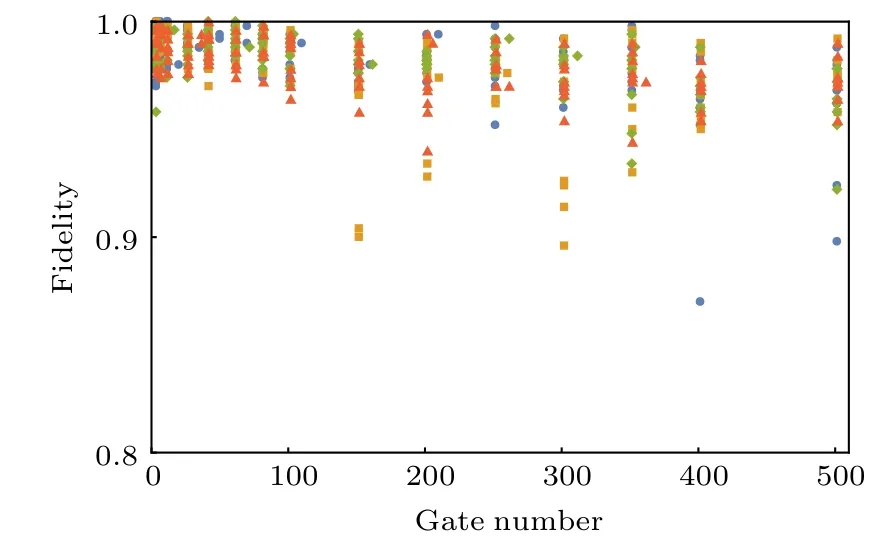
圖5 序列保真度隨序列長度的變化Fig.5. Sequence fidelity pl as a function of the sequence length l.

結合協同冷卻和動力學解耦, 最近我們實現了具有超長相干時間的單比特量子存儲, 并測得超過10 min的相干時間[40]. 我們在標準的Paul阱中同時囚禁171Yb+ 和138Ba+ 兩種離子, 其中171Yb+離子2S1/2電子組態中的兩個超精細能級被定義為量 子 比 特mF=0〉. 在實驗過程中, 持續對138Ba+離子進行激光冷卻. 在測量了系統的環境噪聲譜后, 通過合適的動力學解耦方案, 即脈沖平均間隔的 K DDxy方案, 將環境噪聲漲落對編碼于138Yb+離子之上的量子比特的影響降到最低.

在測量單量子比特相干時間的過程中, 將磁場設定為 3.5 G 來最大限度地減小磁場漲落的影響.選取六個不同的初態, 分別是對于每一個初態執行動力學解耦序列, 并測量拉姆齊條紋的對比度. 以為例, 實驗的脈沖序列如圖6所示. 其中初始化包括多普勒冷卻、激光抽運和 π /2 脈沖. 隨后, 執行一定時間的KDDxy序列, 再執行 π /2 脈沖. 在理想情況下, 最后一個π/2脈沖將系統狀態旋轉到|↑〉. 最后, 測量結果為0或1. 為得到代表拉姆齊條紋對比度的每個實驗被重復30—50次.

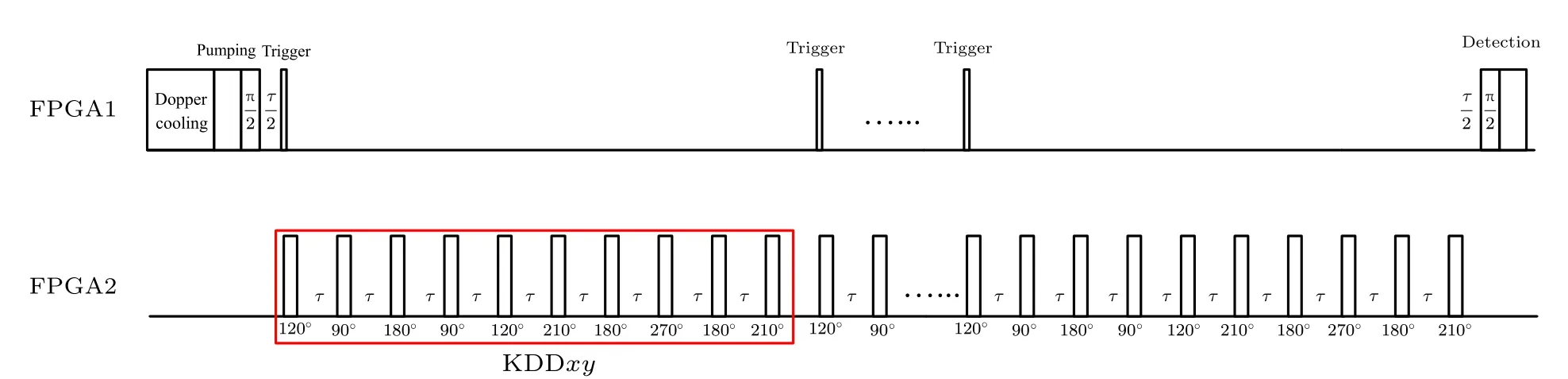
圖6 測量單量子比特相干時間的脈沖序列Fig.6. Pulse sequences for measuring the single-qubit coherent time.

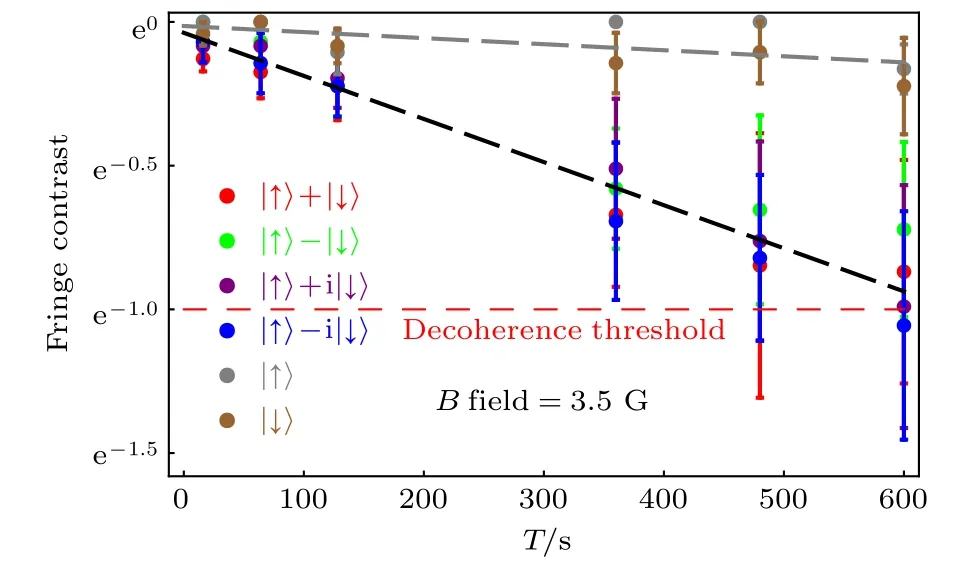
圖7 單量子比特六個不同初態的相干時間, 其中 |↑〉 和 |↓〉 ,對應的相干時間是(4740 ± 1760) s; 其他四個初態對應的相干時間為(667 ± 17) s; 圖中的誤差線代表標準差Fig.7. Single-qubit coherece time for six different initial states. For |↑〉 and |↓〉 , the coherence time is (4740±1760) s. For the other four initial states, the coherence time is (667 ± 17) s. The error bars are the standard deviation.

對每一個初態, 均測量演化時間T后的拉姆齊條紋對比度, 其中600 s}.圖7展示了實驗上測得的六個不同初態在演化時間T后的拉姆齊條紋對比度. 其中,|↑〉和|↓〉的條紋對比度在測量時間內有略微下降, 導致該下降的主要原因是量子邏輯門操作誤差的累積, 對應的相干時間是 ( 4740±1760)s . 其余四個初態對應的相干時間是 ( 667±17)s , 導致退相干的主要原因是動力學解耦的帶通濾波函數中心頻率附近的殘留噪聲譜強度. 上述相干時間是通過對拉姆齊條紋對比度的數據進行指數擬合得到的.

6 總結與展望

在同時囚禁171Yb+ 離子和138Ba+ 離子的混合囚禁離子系統中, 結合協同冷卻和動力學解耦, 本文實現了相干時間超過10 min的單離子量子比特. 雖然超過10 min的單量子比特相干時間已經刷新了此前該領域的世界紀錄, 但我們注意到該相干時間仍然可以進一步延長, 即實現更長的單比特相干時間并沒有基礎原理上的限制. 具體來說, 可以通過以下幾種方式來進一步延長量子比特相干時間: 1) 安裝磁場屏蔽; 2) 使用磁場不敏感的量子比特; 3) 使用相干性更好、相位更穩定的微波源.

如果囚禁更多的用于存儲量子信息的量子比特, 輔以協同冷卻技術, 該系統有望實現量子密碼學領域的理論方案, 包括量子錢幣[5]等. 本文所實現的具有超長相干時間的量子存儲將刺激混合量子計算系統[41,42]的發展, 比如將具有有限相干時間的量子系統中的量子信息映射并儲存到囚禁離子量子比特中.