中性原子量子計算研究進展*

許鵬 何曉東 劉敏 王謹 詹明生?

1) (中國科學院武漢物理與數學研究所, 波譜與原子分子物理國家重點實驗室, 武漢 430071)

2) (中國科學院冷原子物理中心, 武漢 430071)

(2018 年12 月4日收到; 2018 年12 月24日收到修改稿)

相互作用可控、相干時間較長的中性單原子體系具備在1 mm2的面積上提供成千上萬個量子比特的規模化集成的優勢, 是進行量子模擬、實現量子計算的有力候選者. 近幾年中性單原子體系在實驗上取得了快速的發展, 完成了包括50個單原子的確定性裝載、二維和三維陣列中單個原子的尋址和操控、量子比特相干時間的延長、基于里德伯態的兩比特量子門的實現和原子態的高效讀出等, 這些工作極大地推動了該體系在量子模擬和量子計算方面的應用. 本文綜述了該體系在量子計算方面的研究進展, 并介紹了我們在其中所做的兩個貢獻: 一是實現了“魔幻強度光阱”, 克服了光阱中原子退相干的首要因素, 將原子相干時間提高了百倍, 使得相干時間與比特操作時間的比值高達105; 二是利用異核原子共振頻率的差異建立了低串擾的異核單原子體系, 并利用里德伯阻塞效應首次實現了異核兩原子的量子受控非門和量子糾纏, 將量子計算的實驗研究拓展至異核領域. 最后, 分析了中性單原子體系在量子模擬和量子計算方面進一步發展面臨的挑戰與瓶頸.

1 引 言

量子計算是指以量子態作為信息載體, 利用量子態的線性疊加和量子糾纏等量子力學基本原理進行信息并行計算的方案; 以量子計算為基礎的信息處理技術的發展有望引發新的技術革命, 為密碼學、催化化學反應計算、新材料設計、藥物合成等諸多領域的研究提供前所未有的強力手段, 對未來社會的科技、經濟、金融, 以及國防安全等產生革命性的影響[1]. 當前各國政府和大公司紛紛投入巨資開展量子計算的研究, 探索實現量子計算機的各種可能體系, 包括離子阱中囚禁的離子[2]、超導線路[3]、線性光學中的光子[4]、量子點[5]、金剛石NV色心[6]、光阱中的中性原子[7]等. 但由于不同量子體系的操控技術難度和發展應用前景不同[8], 面臨的挑戰也不一樣, 目前哪種體系是最優體系還沒有塵埃落定. 其中, 相互作用可控、相干時間較長且具備擴展優勢的中性原子體系是實現量子計算機的有力候選者之一.

基于中性原子的量子計算, 一般在超高真空腔中利用遠失諧光偶極阱陣列或光晶格從磁光阱或玻色愛因斯坦凝聚體(BEC)中捕獲并囚禁超冷的原子形成單原子陣列, 然后將原子基態超精細能級的兩個磁子能級編碼為一個量子比特的0態和1態. 如圖1所示, 高數值孔徑透鏡將原子比特操控所需的Raman光、里德伯激發光、態制備光等聚焦到單個原子上, 形成對陣列中量子比特的操控. 同時透鏡也收集原子的熒光并傳輸到電子倍增型相機(EMCCD)上實現量子態的探測. 根據收集到的信息和實驗的需要, 通過傳統計算機上的數據采集和時序產生系統, 實時控制原子的冷卻、轉移以及相應的磁場、電場和光場來完成量子算法的執行. 在進行量子計算時, 中性原子體系將根據不同的量子算法, 采用優化后所需邏輯操作數最少的原子陣列構型, 執行一系列高保真的單比特門和兩比特受控非門.

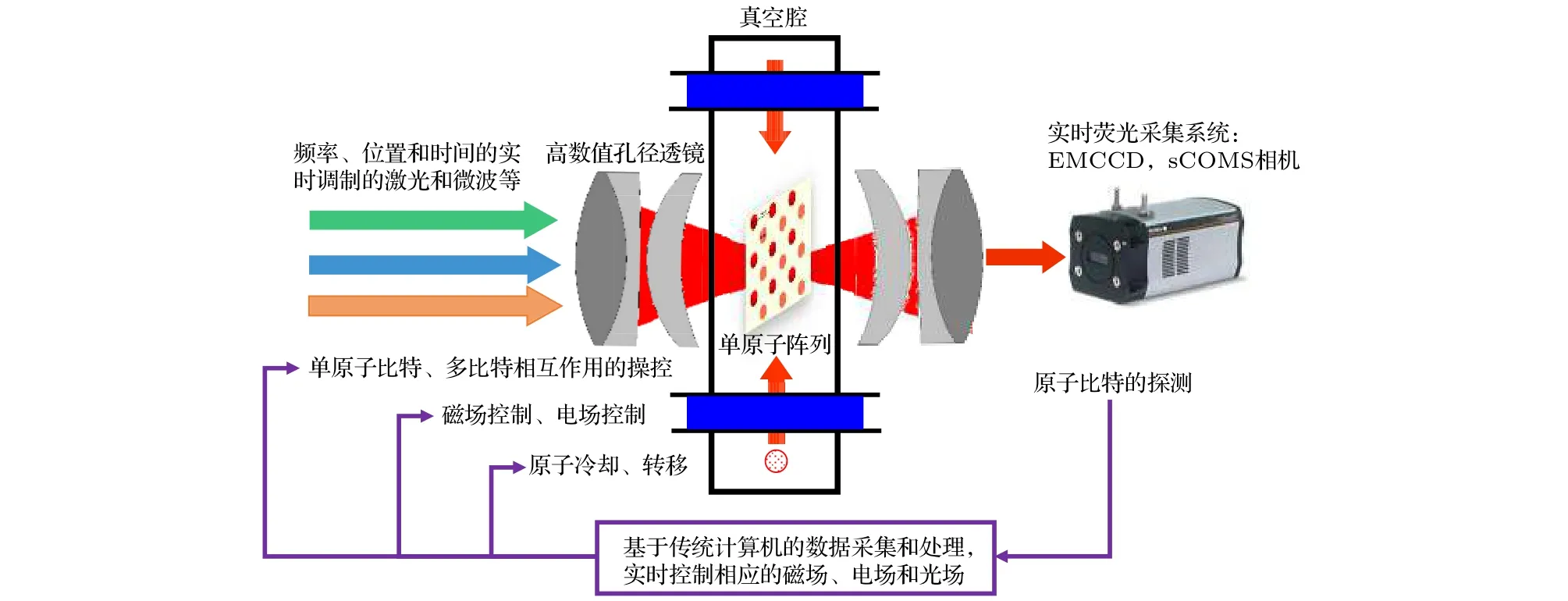
圖1 中性單原子量子計算的概念架構Fig.1. Conceptual architecture for a neutral atom quantum computer.

相比于其他量子計算的候選體系, 基于里德伯態相互作用的中性原子量子計算具備如下3個顯著的特點. 1) 相干時間較長. 相干時間與單比特操控時間的比值是量子計算候選體系的一個重要指標, 中性原子體系采用原子基態超精細能級的磁子能級編碼的量子比特, 目前中性原子體系中單比特相干時間已經可以達12.6 s[9], 相比于原子量子比特操控需要的微秒量級時間, 比率達到 1 07, 這一指標超過了目前大多數量子計算的候選體系.2) 具備可控的相互作用. 相互作用的大小不僅決定了兩比特相位門的操作時間, 而且作用強度的控制對于減少量子算法執行過程中的退相, 提高操作的保真度具有重要的作用. 基于里德伯態原子的偶極?偶極相互作用是一個長程的、強度比基態相互作用大12個量級的相互作用[7], 由此可以將兩比特邏輯門的操控時間控制到微秒以內, 而且該作用可以通過相干激發到里德伯態或從里德伯態相干退激發進行開關, 也可以通過電場、磁場和原子的空間排列來調整大小. 在相互作用可開關的各種量子計算候選體系中, 對于相干時間與兩比特相互作用強度的比值, 主量子數大于50的里德伯態比其他體系更具優勢[10]. 3) 具備很好的擴展性, 且原子陣列的構型靈活可變. 量子計算在編碼邏輯比特執行糾錯算法和進行復雜量子算法時, 對于物理比特數目的要求通常達到數千以上. 目前已報道的量子計算體系中最多的物理比特數目大多集中在50—100個, 對于大多數體系來說, 進一步擴展物理比特數目而不影響操作的保真度都具有很大的挑戰.中性單原子體系不僅可以通過光晶格實現1 mm2的面積上集成數千個單原子[11], 或者在光偶極阱陣列中實現包含72個單原子且構型可變的陣列[12],而且這種靈活可變的中性原子陣列構型, 結合里德伯態原子的多比特邏輯門, 將會有效優化并提高算法的適應性.

近年來, 中性單原子體系在實驗上取得了快速發展, 完成了包括單原子陣列的確定性制備[13,14]、二維(2D)和三維(3D)陣列中單個原子的尋址和操控[15,16]、量子比特相干時間的延長[17,18]、基于里德伯態的兩比特量子門的實現[19,20]和原子態的高效讀出[21,22]等一系列重要的工作, 這些工作極大地推動了該體系在量子模擬和量子計算方面的應用,使得基于里德伯態相互作用的中性原子體系在量子計算的候選體系中得到了越來越多的關注和認可. 本文將介紹該體系量子計算方面的國內外研究進展, 以及我們團隊為該體系的發展所做的兩個貢獻, 即單比特相干時間的延長[17]和異核兩原子糾纏的實現[20], 并對該體系的進一步發展進行了總結和展望.

2 中性原子量子計算研究進展

DiVincenzo[23]總結了一個量子力學系統作為量子計算的候選者必須滿足的5個主要條件, 即DiVincenzo判據, 該判據被認為是實現量子計算機的基本條件. 中性原子體系經過近20年的技術積累和發展, 在可擴展的量子比特(qubit)系統、量子比特初始化、量子比特相干性、通用邏輯門組和量子比特測量方面都已滿足判據的要求.

2.1 實現了可擴展的量子比特的系統

中性原子體系通常采用一個堿金屬原子(如銣原子和銫原子)基態超精細能級的磁子能級作為一個量子比特的0態和1態. 這樣的量子態具備純凈和易操控的特點, 是理想的量子比特. 單個原子捕獲和囚禁則一般用光阱來實現, 主要有兩種方法,一是在光晶格中, 利用Mott絕緣態在每個格點制備一個原子[24], 但由于冷原子云和光場的空間不均勻性, 只有光晶格中心的部分會均勻地裝載; 二是利用碰撞阻塞效應, 當一個光鑷型光偶極阱足夠小時, 阱中兩個以上的原子在共振光的作用下會很快損失掉, 只有一個原子能保存在阱中, 從而獲得單個原子[25], 如圖2所示. 但該裝載是隨機的, 擴展到多個原子陣列時, 無法實現確定性的制備.2016年, 法國Barredo等[13]發展了一種用可移動光阱實現單原子逐個裝配的技術. 他們在2D包含100個光偶極阱的陣列中采用碰撞阻塞的原理隨機裝載單原子, 隨后對光阱陣列進行成像, 判斷出哪些阱中有原子, 然后用一個可移動的光阱將單原子逐個轉移到所需要的光阱中, 從而確定性地制備包含了50個單原子的不同構型的單原子陣列, 隨后他們還演示了包含72個單原子的任意3D構型的確定性制備[12]. 類似的工作還包括美國Endres等[14]在一維(1D)包含50個單原子的陣列中制備演示, 韓國Kim等[26]在2D陣列中通過對轉移算法的優化和對格點中單原子的實時反饋裝載來提高制備效率, Kumar等[27]展示了3D光晶格中利用態依賴的光晶格重排原子得到了5×5×2和 4×4×3 的單原子陣列. 采用單原子裝載后重新排列的方案理論上可以擴展到包含更多單原子的陣列的確定性制備, 從而基本解決了中性原子體系擴展性的問題.

2.2 實現了高精度的態初始化

利用成熟的光泵技術將原子制備到量子比特的|0〉態或|1〉態, 效率可以達到 99.9%以上[28]. 例如, 將銣原子制備到編碼量子比特的|1〉態的F=2,mF=0態時(如圖3所示), 一般采用高斯量級的磁場將不同的磁子能級區分開, 然后用 π 偏振的F=2到F′=2 的 共 振 光配 合F=1 到F′=2 的回泵光, 由于躍遷選擇定則,F=2 ,mF=0 是暗態,經過一段時間的激光作用后, 原子會全部布居到暗態上. 而且由于相同種類的原子能級結構都是一致的, 因此采用同樣的光泵光可以同時實現陣列中所有原子的態初始化.

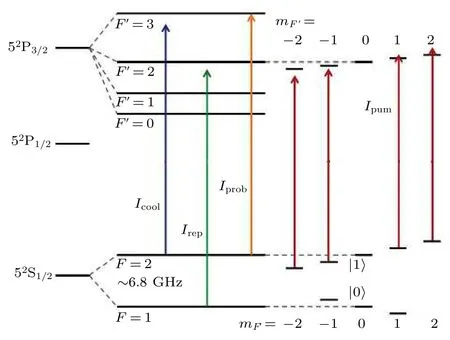
圖3 8 7Rb 原子能級和相關的冷卻光 I cool 、回泵光 I rep 、態制備光 I pum 和態探測光 I prob 對應的躍遷(量子比特的|0〉態和 | 1 〉 態編碼在 F =1 , mF = 0 和 F =2 , mF=0 上)Fig.3. The energy levels and lasers used for cooling,repumpiup ng, optical pumpiup ng, and state detection of 87Rb. The ground hyperfine states of F =1 ,mF=0 and F =2 , mF=0 are used for encoding the qubit.

圖2 遠紅失諧光聚焦形成的偶極阱和偶極阱中收集的單原子熒光信號Fig.2. The optical dipole trap formed by strongly focusing far red?detuned laser. The fluorescence of single atoms trapped by the dipole trap.

2.3 實現了足夠長的量子比特相干時間

要實現量子糾錯, DiVincenzo提出: 量子比特的相干時間需要達到基本量子門操作時間的 1 04倍以上[23]. 在中性原子體系中, 量子比特的相干時間主要由如下三個因素決定[29]. 一是原子在光阱中的囚禁時間, 由于光阱的束縛無法達到離子阱中的勢阱深度, 一般只有毫開量級, 室溫條件下, 背景氣體的碰撞會導致原子的直接損失, 因此即使不考慮光阱本身功率起伏和散射造成的加熱, 原子在光阱的壽命也只有百秒量級. 二是量子比特反轉時間(T1), 主要是由囚禁原子的偶極光引起的拉曼散射造成的, 散射率正比于原子所感受到的光強, 反比于失諧的平方. 對于Rb原子, 1 mK阱深的830 nm光阱中,T1在秒量級. 三是兩基態相對相位丟失時間(T2), 任何改變兩基態能級間隔的因素都會對T2造成影響, 包括原子的熱分布、偶極阱功率的起伏、偶極阱位置的抖動、磁場的起伏等. 德國Kuhr等[29]對光阱中原子退相的三個因素進行了詳細的研究, 在40 μ K 阱深下沒有加任何回波脈沖時, 獲得了相干時間為20 ms的單原子和少原子.Li等[18]建立了中空的藍失諧光阱, 將單個原子囚禁在光強最弱的地方, 從而避免了偶極光引起的退相干, 在沒有回波脈沖作用時, 單個原子的相干時間達到了43 ms. 國內Yang等[17]對單原子的相干時間進行了更深入的研究, 獲得了微型光偶極阱中無回波脈沖條件下目前最長的相干時間, 達到了225 ms. 相對于單原子為微秒量級的操作時間, 其比值也達到了 1 05倍, 滿足了判據對相干時間的要求. Wang等[30]在3D光晶格中獲得了無回波脈沖時26 ms的相干時間, 施加回波后, 相干時間達到7 s以上, 在將原子進一步冷卻到振動基態后, 施加回波得到的相干時間達到12.6 s[9].

2.4 實現了單量子比特門操作和兩量子比特受控非門的操作

中性原子體系中, 單量子比特門操作一般利用與0態和1態能級間隔共振的微波[29]或者一對拉曼光[31]進行操控, 通過控制作用的時間和相位分別控制量子態的布居和相位. 對于單獨一個原子的操控可以簡單地采用上述方案進行, 對于原子陣列,則需要保證對其中一個原子的操控不會影響到其他原子. 2004年, 德國的Schrader等[32]在1D光晶格中, 利用梯度為15 G/cm (1 G = 10?4T)的磁場產生位置依賴的頻率移動, 從而用不同頻率的微波脈沖實現了每個格點中單原子的尋址和操控.在 2D光晶格中, 美國的 Bake等[33], 德國的Sherson等[34]和英國的Haller等[35]分別采用超高數值孔徑的透鏡組(NA＞ 0.68)實現了光晶格中單個格點的分辨. Weitenberg等[36]用該透鏡組將遠失諧的光聚焦到單個格點從而誘導該格點原子的能級發生偏移, 進而用微波脈沖對該原子進行操控而不影響周圍的原子. Xia等[16]在2D的 7 ×7 的單原子陣列中, 采用類似的方法實現了單量子比特的尋址和操控, 并使用隨機基準測試(randomized benchmarking)[37]的方法詳細研究并優化了操控的保真度, 實現了原子陣列中任意一個原子單量子比特操控的保真度達到0.99以上, 而且平均串擾只有0.002(9). 美國的Wang等[30]進一步將該方法擴展到3D光晶格, 采用兩束交叉的尋址光來使目標原子的能級發生偏移, 然后用共振的微波來操作,操作的串擾小于0.003. 隨后, Wang等[15]采用類似的尋址光, 并利用尋址光累積的相位結合一系列微波脈沖, 實現了一種對尋址光的不穩定非常不敏感并且具備很低串擾的新的尋址和操作方法, 操作的保真度達到0.9962(16), 串擾小于0.002.

兩量子比特糾纏門的實現是中性原子量子計算的核心. 受限于中性原子間微弱的相互作用, 目前實現兩原子量子比特糾纏的方案主要有三種: 一是將與原子糾纏的光子進行貝爾態測量來制備糾纏的原子. 代表性工作是2006年Volz等[38]將單原子激發后, 利用自發輻射, 實現輻射單光子的偏振與單原子磁子能級的糾纏, 在此基礎上制備兩組糾纏的單光子和單原子, 然后對兩個光子進行貝爾態測量, 獲得糾纏光子對的同時通過糾纏交換實現兩個原子的糾纏[39]. 該方法產生糾纏的過程不可控且效率較低, 并不適合作為量子計算中的邏輯門. 第二種是基于原子基態受控碰撞的方案[40,41], 通過調節同一個阱中兩個原子的振動態、電子態, 或者通過精確調制兩個阱的間距來控制隧穿進而控制兩個原子自旋碰撞交換相互作用, 實現兩量子比特糾纏門. 目前已經在光晶格中實現了兩團原子間基于碰撞的糾纏和受控相位門[42,43]. 對于兩個原子間的糾纏, 美國的Kaufman等[44]和美國的Thompson等[45]分別在強聚焦光偶極阱中, 通過Raman邊帶冷卻將原子冷卻到振動基態, 隨后Kaufman等[46]精確控制兩阱的相對位置, 基于自旋交換實現了保真度為0.44的兩原子糾纏, 扣除原子損失后, 糾纏的保真度達到0.63. 該實驗受限于原子在光阱中三個維度的冷卻效率和對兩原子間距的控制精度, 進一步提高保真度面臨很大的挑戰. 第三種方案是基于原子里德伯態的偶極?偶極相互作用實現受控非門, 包括采用里德伯阻塞形成受控相位門[47], 利用共振的偶極?偶極相互作用形成的兩原子暗態進行絕熱演化[48], 利用里德伯綴飾形成受控相位門[49]等. 實驗上, 美國的Urban等[50]在相距8 μ m 的兩個微型光偶極阱中分別囚禁了單個銣原子, 然后將其中一個原子相干激發到97D的里德伯態, 此時另一個原子的里德伯能級由于偶極?偶極相互作用發生偏移, 從而無法實現里德伯的激發. 利用該效應, Isenhowe等[19]首次實現了兩個中性原子間的受控非門, 保真度達到0.73, 并進一步實現了兩原子糾纏, 糾正原子損失后保真度為0.58. 法國的Ga?tan等[51]和Wilk等[52], 將單原子囚禁在兩個相距4 μ m 的偶極阱中, 將兩個銣原子的初始態制備為 |1〉 態, 在58D的里德伯態激發光的作用下, 利用相同的里德伯態相互作用實現里德伯阻塞, 則只有一個原子被激發, 于是兩原子被制備到基于里德伯態的兩原子糾纏, 隨后施加一個將里德伯原子耦合到激發光, 相干轉移到基態, 獲得基態兩原子的最大糾纏態, 保真度在糾正原子損失后達到0.75. 采用原子里德伯態偶極?偶極相互作用實現兩量子比特糾纏門對于原子熱運動并不敏感, 而且門操作時間在微秒量級, 是目前最適合中性原子體系的兩量子比特門方案. Zhang等[53]和Maller等[54]從理論上對該方案進行了細致的分析和模擬, 并在實驗上對相關技術噪聲進行了進一步的優化, 目前得到的保真度為0.82, 但距離實現糾錯的0.99的閾值還有很大差距, 需要進一步研究和優化.

2.5 實現了量子態的測量與讀出

為獲取量子計算的結果或執行糾錯算法, 必須對量子態進行方便而快速的測量. 中性原子體系對原子0態和1態的測量普遍采用的方法是用共振激光將1態的原子加熱從而在阱中損失掉, 如圖3中的探測光. 由于加熱所需的散射光子數依賴于阱深, 因此可以通過降低阱深減少散射的光子, 從而避免在探測過程中由于共振光的拉曼躍遷改變原子的狀態, 提高探測的保真度[55]. 該方法的缺陷在于每次探測導致原子損失, 需要重新裝載單原子,不利于提高實驗速率. 隨后, 法國的Fuhrmanek等[56]和美國的Gibbons等[57]同時用高數值孔徑透鏡提高原子熒光收集效率, 并仔細優化探測光頻率與閉合躍遷能級的共振來抑制拉曼躍遷, 實現了95%以上的態探測效率, 同時原子的損失只有1%. 美國的 Kwon 等[21]和德國的 Martinez?Dorantes等[22]進一步將該方法拓展到2D原子陣列, 用共振光同時激發原子陣列中所有原子, 并用電子倍增型相機收集熒光進行態的探測, 態的探測效率都大于97%, 且原子損失小于2%.

在該體系的發展過程中, 國內多個研究小組也都做出了各自的貢獻. He等[58]在偶極阱中實現了捕獲時間為130 s的單個銫原子, 并開展了兩方面與量子計算相關的研究工作, 一是利用單原子制備單光子源; 二是研究單原子與高細度微腔的耦合.中國科技大學Dai等[59]采用光晶格來囚禁和操控銣原子的BEC, 利用光極化勢形成了有效磁場梯度, 來調控原子間相互作用, 進而開展拓撲量子計算方面的研究工作. 詹明生等[60,61]自2009年利用強聚焦光偶極阱實現了單個銣原子的囚禁以來, 圍繞中性原子量子計算, 克服了單原子量子比特的精確操控、兩原子量子比特相互作用的有效調控和多量子比特陣列的制備等一系列關鍵物理問題和技術難題, 在中國科學院武漢物理與數學研究所初步建立了滿足DiVincenzo判據的中性單原子量子計算平臺; 在此基礎上, 發展了“魔幻強度光阱”的方法和低串擾的異核單原子陣列, 實現了中性單原子體系在相干時間和原子陣列中串擾抑制方面的突破, 并開展了異核原子碰撞和量子糾纏的工作, 將該體系量子計算的實驗研究進一步拓展到了異核領域. 以下將詳細介紹單量子比特相干時間的延長和異核兩原子糾纏的實現.

3 魔幻強度光阱延長量子比特的相干時間

如前所述, 中性原子量子比特的相干時間主要受限于基態相對相位丟失時間T2. 實驗研究表明,用于編碼量子比特的超精細能級劈裂通常有幾個GHz大小, 由此導致光阱中的量子比特的0態和1態光頻移不同, 即微分光頻移, 這是導致T2減小的主要因素. 例如, 由于熱分布, 原子在偶極阱中的不同位置所感受到的光強不同, 從而導致微分光頻移的大小不同, 所以原子的共振頻率會被原子的熱運動展寬(通常在100 Hz的量級), 該展寬會直接導致原子量子比特的非均勻退相. 雖然在靜態偶極阱中該非均勻退相可以被動力學退耦的辦法(如自旋回波或CPMG脈沖序列)有效地抑制[62], 但是實驗上發現, 動力學退耦的方法很難抵消單原子量子比特轉移中的相干性丟失. 這是由于在用移動光鑷將原子從某個偶極阱轉移到另外一個偶極阱的過程中, 光場是動態變化的. 移動光鑷的指向起伏以及原子加熱所導致的退相都是頻率較高的均勻退相, 通常的動力學退耦的方法很難壓制[63]. 另外一個方面的問題是, 量子比特的能級展寬也會造成單量子比特的操控誤差[15,16]. 因此, 降低微分光頻移對相干時間的影響可以更好地提高原子量子比特的質量, 并突破相干時間對大規模中性原子量子信息處理平臺實現與應用的限制.

3.1 魔幻強度光阱的構建和相干時間的延長

2010年, Derevianko[64]以及 Lundblad等[65]提出和演示了可以利用矢量光頻移抵消微分光頻移的方案. 為了誘導矢量極化率, 即等效磁場, 基本的實驗方案是, 將囚禁光場從原來的線偏振改為圓偏振, 同時將光的偏振矢量的方向與量子化軸的磁場方向設為一致. 由此得到微分光頻移為其中B為量子化軸磁場,β1為標量光頻移系數,β2為矢量極化率與塞曼相互作用導致的3階交叉項的系數,β4為基態超極化率系數,Ua為偶極阱的阱深. 他們發現,在弱場極限條件下, 光場誘導的原子的4階超極化率β4可以忽略, 從而可以得到一個“魔幻磁場”囚禁條件, 即在一個特定的磁場下(通常需要幾個高斯), 微分光頻移能夠被矢量極化率與塞曼相互作用導致的3階交叉項所抵消. 但是實驗上為了囚禁溫度為十幾微開的單原子量子比特, 光鑷所需的光場較強, 這時光場誘導的等效磁場達到高斯量級,與外加磁場可比擬, 因而弱場近似不成立, 高階項即超極化率不可忽略. 而且由于超極化率的貢獻,光頻移是勢阱深度的二次函數. 實驗上, 考慮到β2和β4也依賴于偶極光的圓偏振度, 為簡單起見, 我們采用完全相同的圓偏振光, 測量了不同阱深和磁場下原子所感受到的微分光頻移, 結果如圖4(a)所示. 采用圓偏振阱中去擬合, 得到β2為并且首次測量了87Rb 原子的超極化率該結果與理論計算結果相符合.

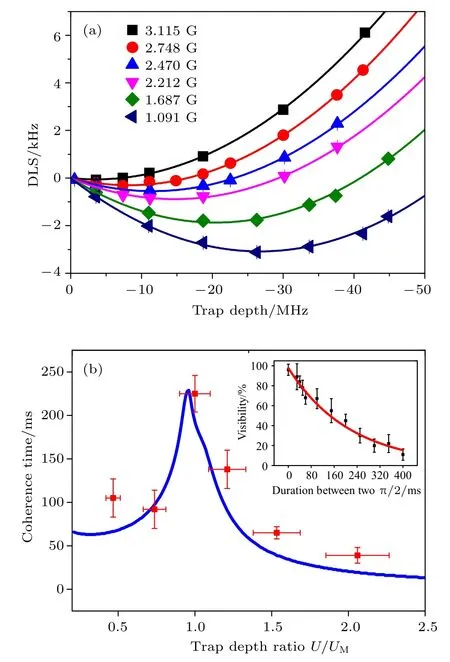
圖4 (a)超極化率不可忽略情況下, 原子量子比特的微分光頻移在不同磁場下隨偶極阱勢深的變化; (b)原子量子比特相干時間在不同偶極阱勢深下的實驗值, 藍色實線為理論值; 內插圖顯示了阱深為 時, 通過擬合Ramsey條紋的對比度得到相干時間為 ms[17]UM τ=(225±21)Fig.4. (a) In the presence of hyperpolarizability, the differential light shift (DLS) of a qubit in the circularly polarized trap is measured as a function of trap depths at various magnetic field strengths; (b) coherence time and its dependence on normalized ratios obtained from experiment. The solid blue line is the theoretical curve. A coherence time is extracted from a decay time of the envelope of Ramsey visibility, as shown as in the inset. At, ms[17].τU/UM Ua=UM τ=(225±21)

由于不可忽略的超極化率的貢獻, 原子量子比特頻率的展寬程度依賴于勢阱深度. 理論上, 在微分光頻移對勢阱深度的一階偏微分等于0的位置,即展寬最小, 因而是魔幻光強點. 在該偶極阱阱深附近, 原子的微分光頻移對于勢深起伏的敏感性降到二階. 在特定磁場趨近于 0, 此時阱深太淺不利于原子的囚禁, 因此一般選用更小的磁場和稍大一點的阱深進行實驗. 在綜合考慮微分光頻移和偶極光散射引起的退相的因素后, 實驗上選取的磁場強度為3.115 G, 通過測量Ramsey條紋的衰減時間隨勢阱深度的變化曲線, 發現相干時間最長的地方就在微分光頻移的極值點附近, 如圖4(b)所示. 最長的Ramsey條紋的衰減時間達到 ( 225±21) ms, 而在線偏振偶極阱中是(1.4±0.1)ms[62], 相干時間提高了百倍. 相比于Li等[18]在中空的藍失諧光阱中獲得的銫原子43 ms的Ramsey相干時間, 我們的結果提高了5倍. 需要強調的是, 紅失諧魔幻光強偶極阱比中空的藍失諧光阱更加便于擴展到較大規模的魔幻偶極阱陣列.這是由于紅失諧的單阱所需功率只需毫瓦量級, 而中空的藍失諧光阱的功率要到達百毫瓦量級.

3.2 相干轉移的實現

在大規模的單原子陣列里, 受限于中性原子間微弱的相互作用, 要實現任意兩個原子間的量子算法進而實現量子計算和量子模擬, 需要將單原子相干地轉移到相互作用區. 我們提出了一種簡單易行的深阱轉移方案, 實現了單原子在光阱陣列中的高效轉移(約95%), 但在轉移過程中, 即使采用動態退耦的方法也無法保持量子比特的相干性, 主要原因在于偶極光引起的微分光頻移[63]. 運用魔幻光強偶極阱技術(圖5所示), 首先在其中一個魔幻光強偶極阱中(trap 2)制備一個量子比特, 通過微波制備到相干疊加態上, 之后通過一個移動魔幻阱(trap 1)將目標量子比特提取出來轉移到5 μ m 的地方后再送回原來的偶極阱, 而后分析量子比特的相干性. 結果發現無轉移和被轉移的量子比特的Ramsey相干時間幾乎一致, 因此在實驗的測量精度內, 沒有觀測到原子的相干性在進行轉移操作后有明顯的損失, 即使轉移后原子的溫度從8 μ K 升到16 μ K . 因此, 實驗上證明了用魔幻光強偶極阱轉移原子量子比特的過程中, 指向漲落、加熱等退相因素變得很小. 然而線偏振阱中這些退相機制是占主導的. 由此解決了中性單原子大規模陣列中單原子相干轉移的問題, 極大地提高了原子量子比特間的互聯性, 該方法與原子量子比特陣列靈活的構型互相結合, 將有效地降低中性原子量子計算算法的復雜性.

3.3 魔幻光強偶極阱中原子退相的主要因素

圖5 (a)原子量子比特相干轉移的實驗裝置示意圖(Trap 1是可移動阱, 其在焦平面上的位置由2D聲光偏轉器控制; Trap 2是靜止阱; 兩阱的偏振可以通過液晶相位片 (Thorlabs LCR?1?NIR)實時控制); (b) 原子量子比特在兩阱中不轉移(黑色方塊)和轉移(紅色圓點)時的Ramsey條紋(實驗數據中每個點是100多次實驗的平均值; 通過衰減的正弦函數擬合(實線部分), 可以得到靜止量子比特和轉移量子比特的相干時間分別是(206 ± 69) ms和(205±74) ms[17]Fig.5. (a) Experimental setup for coherent transfer of atomic qubit. Trap 1 is a movable trap which can be shiftted in two orthogonal diretions by an AOD. Trap 2 is a static one. Both of their polarizations can be actively controlled by a liquid crystal retarder (LCR). (b) Measured Ramsey signals for single static qubits (black squares) and single mobile qubits (red dots) at B =3.115 G. Every point is an average over 100 experimental runs. The solid curves are fits to the damped sinusoidal function, with coherence times of static qubits and mobile qubits are (206±69) ms and (205 ± 74) ms, respectively[17].

由原子結構以及光和原子作用參數決定, 構建魔幻光強偶極阱需要3.2 G的磁場, 導致量子比特對磁場噪聲變得敏感. 通過對磁場的監視和對自旋回波的實驗測量, 我們詳細分析了魔幻光強偶極阱中量子比特相干時間的影響因素, 如表1所列. 從中發現相干時間主要受限于磁場的噪聲. 為了壓制磁場噪聲, 可以搭建磁屏蔽來消除背景的磁場噪聲, 但更有科學價值的是尋找磁場的魔幻條件, 使得量子比特對于磁場噪聲的敏感性降到2階.Carr和Saffman[66]提出一個理論方案, 利用雙色光場實現更低的磁場噪聲敏感度來提高銫原子的相干時間. 目前還未有實驗演示中性原子體系中的雙魔幻囚禁, 即同時將量子比特對于勢深以及磁場噪聲的敏感性降到2階. 這樣的實驗具有挑戰性, 但對于中性原子量子比特來說是非常重要的.

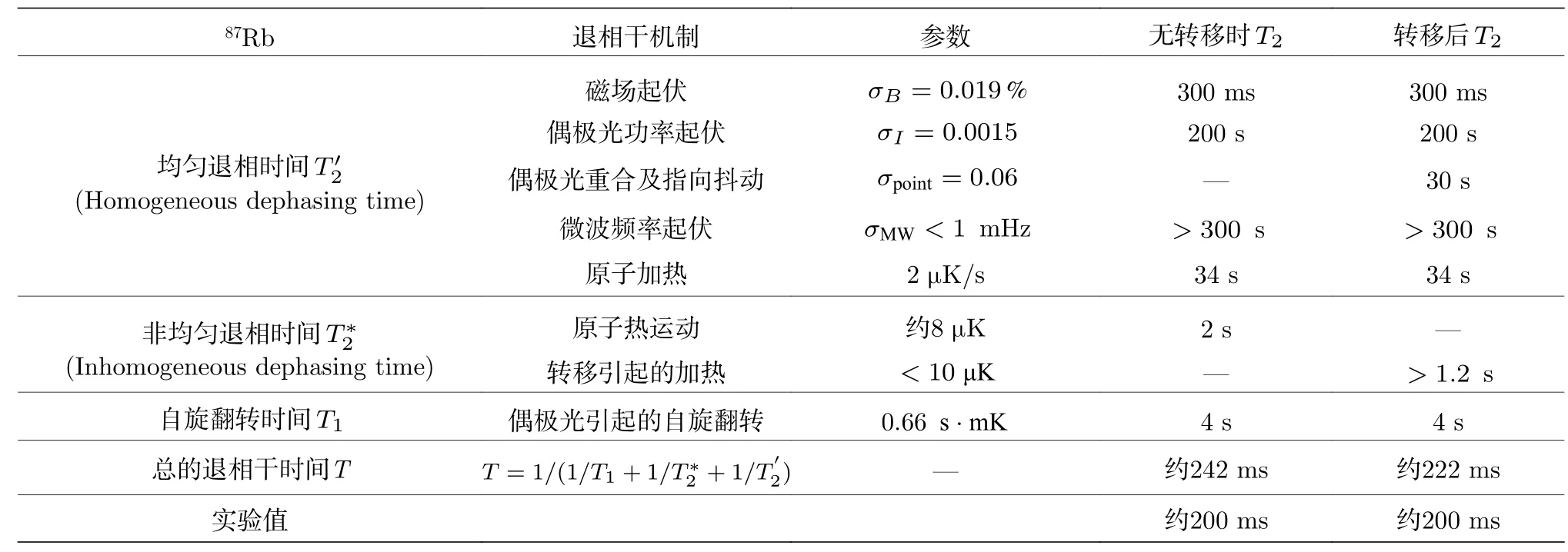
表1 魔幻光強偶極阱中的退相干機制Table 1. The mechanisms of decoherence in magic intensity optical trap.

4 基于里德伯阻塞的異核兩原子受控非門與量子糾纏的實現

正如Saffman[11]在基于里德伯態原子相互作用的中性單原子量子計算綜述中指出的, 中性原子體系距離實現量子計算機還有諸多難題, 目前面臨的主要挑戰包括更高保真度的糾纏門操作、原子的再裝載、原子態的無損讀出、量子比特間距在微米量級的陣列中低串擾的測量和初始化以及表面附近電場噪聲的控制. 其中, 針對原子態的無損讀出、量子比特間距在微米量級的陣列中低串擾的測量問題, Beterov和 Saffman[67]提出了建立異核單原子體系, 利用異核原子共振頻率的差別來避免串擾, 并利用異核原子間的糾纏來解決無損探測的方案. 相比于同核體系, 異核單原子體系中不同種類的原子可以用于執行量子計算中不同的任務, 如Auger等[68]提出采用一種原子量子比特作為糾錯碼中的校驗子, 另一種原子作為數據量子比特, 可以有效地執行糾錯并避免串擾. 類似地, 在囚禁離子體系中, 也有兩個異核離子間的受控非門的實驗, 并且展望了兩種離子分別作為量子存儲和光接口以及在量子非破壞性測量中的應用[69,70]. 在量子模擬中, 異核體系提供了額外的操控自由度, 為多組分多自旋體系的模擬提供了必備的條件, 如Weimer等[71]提出利用異核單原子作為輔助量子比特, 來克服量子態操作時的串擾, 以模擬帶耗散的量子自旋體系的相干演化; 華東師范大學Qian等[72]提出在1D異核原子陣列中研究豐富的動態相位演化等. 由此可見, 基于里德伯阻塞的異核原子的受控非門和量子糾纏在量子模擬、量子計算和量子精密測量等領域都有廣泛的應用.

4.1 里德伯態的原子及其相互作用

里德伯態原子是指原子中的一個電子被激發到主量子數較高的軌道時的原子. 由于電子遠離原子核, 里德伯態的壽命相對于低激發態的壽命要長很多, 對電場也更加敏感等. 里德伯阻塞是利用里德伯態原子間強烈的偶極?偶極相互作用或范德瓦耳斯相互作用, 使得一定區域內一群原子同時激發時, 只有一個原子能被激發到里德伯態, 而其余原子由于相互作用導致能級發生偏移, 因而失諧于激發光, 無法被激發.

里德伯態原子間的相互作用的大小決定了里德伯阻塞效應及后繼的受控非門的保真度. 當里德伯態主量子數小于100時, 由于里德伯原子的半徑小于0.5 μ m , 遠小于原子間的普遍間距R(3 μ m 以上), 因此兩個里德伯原子A和B之間的相互作用可近似為其中a和b分別是兩個里德伯電子距離各自原子核的位置. 在兩原子間距R比較大時, 原子間的相互作用Vdd可視為微擾, 相應的能級移動 ?En可采用二階微擾計算得到為其中此時的相互作用與R6成反比, 對應經典的范德瓦耳斯相互作用; 而當R較小, 原子相互作用大到足以導致原子鄰近能級混合時, 即Vdd≥δ時, 其中為鄰近里德伯能級組合與原里德伯能級的差, 兩原子體系的哈密頓量需要選擇新的基矢重新對角化, 其相互作用導致的能級移動將變為此時的相互作用與R3成反比, 對應于共振的偶極?偶極相互作用[7]. 針對實驗中采用的85Rb 和87Rb 異核原子的里德伯態的相互作用, 考慮到兩種原子里德伯態能級的差別, 由量子數決定的雙原子態在主量子數為79D時有436個組態, 將相互作用的哈密頓量在兩原子態構成的子空間展開并求解里德伯阻塞的能級移動. 并進一步考慮到實驗中單原子在偶極阱中的熱分布, 由此得到且偶極阱束腰為2.1 μ m ,兩阱間距3.8 μ m , 阱深為0.1 mK時, 異核兩原子間典型的相互作用強度為200 MHz, 兩原子同時激發到里德伯態的概率約為1.3%.

4.2 單原子里德伯態的相干激發

實現原子從基態到里德伯態的相干激發是實驗的第一步. 由于里德伯態的主量子數很高, 使用單光子將原子從基態激發到里德伯態需要短波長的激光. 對于銣原子, 單光子激發波長在297 nm左右, 對于銫原子, 需要318 nm的激光. 國內山西大學Wang等[73]采用和頻加倍頻的方案產生了2.26 W的318 nm激光, 而且該激光波長可調范圍覆蓋了銫原子從n=70 到電離態的所有能級. 我們在實驗中采用 780 nm + 480 nm的雙光子激發方案, 780 nm激光由普通的半導體激光器產生,而480 nm激光由960 nm激光倍頻獲得(Toptica SHG). 相對于單光子激發, 雙光子激發所需的激光波長和激光功率比較容易實現, 而且采用對射的激發方案可以有效地減少激發過程引起的多普勒展寬, 但雙光子激發也會引起中間能級的布居形成自發輻射損失, 造成激發效率的降低. 因此在實驗中,雙光子激發需要考慮對中間能級的失諧和激發光的光強, 來平衡基態到里德伯態的激發速度與中間態布居引起的自發輻射損失.

由于原子里德伯態的壽命可以到幾十到幾百微秒, 對應的里德伯態的自然線寬可以到幾十千赫茲, 因此用于里德伯態相干激發的激光的線寬和頻率的長漂也必須控制到相應的量級[74]. 簡單地估算, 用π脈沖將原子從基態相干地激發到里德伯態時, 激發效率的損失正比于其中?是雙光子失諧,?是基態到里德伯態的有效Rabi頻率. 當Rabi頻率為 2 π×1 MHz, 且激發效率的損失小于10-4時, 則要求?/2π 小于 10 kHz. 由此可見, 實現高效率的里德伯態的激發不僅需要將激發光的線寬和頻率的長漂控制到10 kHz量級, 同時也要控制背景電場和磁場, 避免里德伯態能級的移動超過10 kHz.

對于里德伯態激發光的穩頻, 最初采用的電磁誘導透明(EIT)的峰來鎖定, 但無法壓窄激光器的線寬, 同時頻率的長漂在百千赫茲量級. 目前大多數實驗小組采用的是高精細度的超穩腔來將激發光的線寬壓窄到千赫茲量級, 但激光頻率的長漂通常在百千赫茲量級, 如Pritchard[75]小組用超穩腔將銫原子的里德伯激發光線寬壓窄到260 Hz, 但激光頻率的長漂為86 kHz/d. 為避免激光頻率的長漂, 我們定制了一個可調節腔長的高細度傳輸腔(Stable Laser Systems公司)進行穩頻. 該腔在780, 960和1064 nm的細度分別是9.1萬、5.9萬和8.7萬, 同時腔長變化一個1.5 GHz的自由光譜程可以通過在腔鏡的PZT上施加0—75 V的電壓實現. 先將傳輸腔的腔長鎖定到一個商用的碘穩激光器(Innonlight, Coherent)上, 這個激光器的線寬約為1 kHz, 長漂在1 kHz/0.5°C . 然后將里德伯態的激發光780和960 nm (480 nm 的種子光)通過 Pound?Drever?Hal (PDH)頻率穩定的方法鎖定到腔長穩定的超腔上. 鎖定后, 通過延時自拍頻的方法標定780和480 nm激光的線寬分別是12.6和10.8 kHz, 并通過里德伯態的吸收峰得到兩個激發光頻率之和的長漂小于33 kHz/10 h[76].

里德伯激發光脈沖的功率漲落會引起原子能級的AC Stark頻移的變化, 從而導致基態到里德伯態的躍遷頻率發生改變. 在實驗當中, 780 nm的激發光引起原子基態AC Stark頻移大小約為2π×3MHz. 激光功率不進行穩定時, 功率的長漂在10%左右, 這個值對應的原子基態能級的變化達到2 π ×3 00 kHz. 因此我們采用類似Noise eater的方案將480和780 nm激發光的功率進行穩定,長時間功率漂移控制到0.1%以內以滿足實驗需求. 此外, 里德伯態原子的極化率正比于n7, 因此其能級對外電場非常敏感. 例如, 處于5/2態的銣原子, 當外電場為0.1 V/cm時, 其能級偏移約為27 MHz. 因此當里德伯態的原子距離真空腔或透鏡表面只有幾個毫米, 許多實驗小組在介質表面鍍ITO的導電膜來屏蔽外電場的干擾[77,78],并減少銣原子吸附在介質表面時產生的電場的干擾[79]. 實驗系統中原子囚禁的位置距離真空腔達到12 mm, 而且由于系統一直使用銣原子的釋放劑作為銣源, 導致整個真空系統內壁鍍一層銣原子薄膜, 對外電場有很好的屏蔽作用. 在我們的實驗中, 即使外電場從0變化到26 mV/cm, 都沒有看到的里德伯能級有顯著移動.

在具備以上實驗條件后, 實現了對單個銣原子從基態到里德伯態的相干激發. 采用對中間能級失諧 3—4 GHz 的 大 失 諧, 將 5.6 μ W 的σ+偏 振 的780 nm激發光聚焦到約8 μ m , 51 mW的σ+偏振的480 nm激發光聚焦到約12.8 μ m , 獲得的單個

87Rb 原子從基態5 S 1/2 ,F=2 ,mF=0 到里德伯態79 D5/2,mj=5/2 的Rabi振蕩如圖6所示. 激發過程中, 480 nm的激發光始終打開, 通過控制780 nm激發光的作用時間控制里德伯態的激發. 里德伯態的探測則是利用里德伯態原子在偶極阱中的損失來探測, 其損失來源于830 nm的偶極阱對于里德伯原子的排斥和偶極光對里德伯態原子的電離. 原子激發到里德伯態的效率通過詳細分析將原子全部轉移到里德伯態后剩余原子的內態布居得到, 可以得到激發效率約為96%, 由此對應的里德伯態的探測效率約為90%.

4.3 異核受控非門

從單個原子的里德伯態相干激發擴展到兩個不同原子的里德伯態間的相互作用, 首先需要構建兩個異核原子的陣列. 我們采用類似圖5(a)的設置, 利用兩束830 nm的激光建立了兩個偶極阱,分別裝載單個87Rb 原子和單個85Rb 原子. 由于光偶極阱中單原子的裝載是一個隨機過程, 需要等待

單原子進入偶極阱來實現單原子的囚禁, 因此先打開阱1裝載87Rb , 然后打開阱2裝載85Rb , 再利用后選擇的方案, 確保裝載完成后異核單原子位于對應的光阱中[80]. 異核體系最大的優勢在于異核原子共振頻率的不同, 可以有效地避免操作的串擾, 并且可以利用激光頻率的差別實現兩原子的獨立尋址. 我們的實驗裝置中, 所有的激光同時覆蓋兩個異核原子, 對兩個異核原子的單獨操控是利用不同頻率的激光完成的. 如圖6所示, 對于87Rb 和85Rb原子, 其基態能級的頻率差最小為1.1 GHz左右, 利用該頻率差別, 進行87Rb 的里德伯態相干激發時, 對85Rb 原子的串擾可以忽略,85Rb 原子幾乎沒有任何激發.

如前所述, 理論計算顯示兩個異核原子在79D里德伯態時, 異核里德伯阻塞效率可以達到98.7%. 實驗上, 首先用 π 脈沖將87Rb 原子從基態激發到79D里德伯態, 然后等待0.3 μs , 再測量85Rb原子的基態到里德伯態Rabi振蕩. 由于79D里德伯態的壽命達到180 μs , 可以提供足夠長的相互作用時間, 而且實驗中僅記錄時序完成后87Rb 不在阱1中的事件, 由此排除87Rb 沒有激發到里德伯態的事件. 如圖7所示, 我們在實驗上首次展示了異核里德伯阻塞, 當阱1中沒有87Rb 原子時, 阱2中的85Rb 展示了很好的基態到里德伯態相干Rabi振蕩; 而阱1中的87Rb 激發到里德伯態后,阱2中的85Rb 里德伯激發被極強地抑制了, 激發效率只有約3%, 與理論預期相符合.85Rb 的里德伯激發沒有被完全抑制, 主要原因是實驗中阱1的87Rb原子由于其他原因造成的損失被計入到有效阻塞事件中引起的誤差.

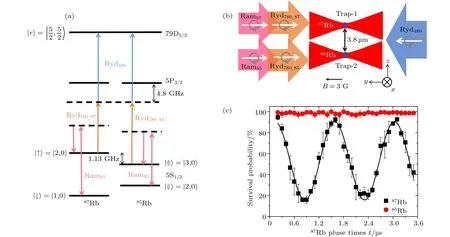
圖6 (a) 8 5Rb 和 8 7Rb 的能級及相應的激光; (b) 實驗光路示意圖; (c) 8 7Rb 原子在 |↑〉 和 |r〉 態間的相干Rabi振蕩; 里德伯態激發光同時作用到 8 5Rb , 由于頻率的差別, 8 5Rb 沒有任何激發, 兩原子間操作的串擾可忽略[20]Fig.6. (a) Energy levels and lasers of 8 5Rb and 8 7Rb ; (b) experimental setup; (c) the coherent Rabi oscillation between |↑〉 and|r〉of 8 7Rb , there is no excitation of 8 5Rb although the Rydberg excitation lasers also act on it which shows negligible crosstalk between two atoms[20].

基于里德伯阻塞實現兩原子受控非門的關鍵在于兩原子處在不同能級時的相互作用強度. 當兩個原子都處在基態時, 主要的相互作用是磁偶極相互作用. 若原子間距約4 μ m , 相互作用換算成頻率在 1 0-3Hz量級. 當其中一個原子激發到里德伯態后, 相互作用主要是基態與里德伯態的二階偶極?偶極相互作用, 間距約4 μ m 時強度約為 1 0-3Hz量級[28]. 而當兩個原子同時激發到里德伯態后, 由于里德伯態具備的巨大的電偶極矩, 他們之間的相互作用達到共振的偶極?偶極相互作用的極限, 其強度將得到量級上的提升, 可以達到100 MHz以上. 因此可以通過如下步驟形成受控的相位門:1)將“控制”原子用 π 脈沖激發從|1〉態激發到|r〉,處在|1〉態的原子將變成-i|r〉態; 2)在“目標”原子上施加2 π 脈沖激發|1〉態和|r〉, 沒有里德伯阻塞時, 處在|1〉態的目標原子將變成-|1〉態, 有里德伯阻塞時, 態不變; 3)將“控制”原子用 π 脈沖激發從|r〉態退激發到|1〉, 處在-i|r〉態的控制原子將變成-|1〉. 因此在|0 0〉,|0 1〉,|1 0〉,|1 1〉的兩原子基矢下,可以得到受控相位門Cz=diag(1,-1,-1,-1)[28].再結合兩個Hadamard門, 即可將受控相位門轉變為受控非門.

采用該方案, 我們在實驗中以87Rb 原子的5 S1/2,作為控制量 子 比 特|↑〉和|↓〉態 ,85Rb 原 子 的 5 S1/2,F=3 ,mF=0和5 S1/2,F=2,mF=0 作為目標量子比特|?〉和|?〉態. 如圖8(b)所示, 得到輸出態的布居隨著兩個Hadamard門的相對相位的振蕩, 體現了C?NOT門操作的內在相干性. 當設定相對相位為 π 時,87Rb 處于|↑〉態, C?NOT操作會翻轉85Rb的態. 通過測量C?NOT門的真值表, 得到異核C?NOT門操作的保真度為0.73(1). 該保真度主要受限于里德伯態的激發效率和初態制備的效率. 實驗中里德伯態的激發效率只有96%, 主要原因在于里德伯態激發光鎖定到超高細度FP腔時, 為了壓窄線寬, 激發光高頻部分的相位噪聲有所增加, 從而導致了基態到里德伯態Rabi振蕩的退相[81], 降低了里德伯態的激發效率. Levine等[82]最近展示了利用超高細度FP腔過濾激發光的高頻相位噪聲, 實現了高效的里德伯態激發和保真度達到0.97的里德伯態原子的糾纏. 這也是我們在實驗上下一步需要進行的工作. 異核C?NOT保真度的另一限制因素是初態的制備效率只有0.91 (如圖8(c)), 主要原因在于基態Raman光功率起伏造成躍遷效率的變化和實驗過程中背景氣體以及原子在兩阱間的轉移造成的損失. 這一部分損失將通過改進實驗條件加以抑制.

4.4 異核兩原子糾纏

異核受控非門可用于確定性地實現異核兩原子的糾纏態. 當用基態 π /2的Raman脈沖作用到87Rb 原子上, 就可以制備或者的初態, 然后執行異核C?NOT門, 就可以得到兩種Bell糾纏態或者為確定實驗得到的是糾纏態, 一般通過測量宇稱信號來獲取糾纏的保真度. 實驗上, 首先制備然后對兩個原子分別施加基態π/2的Raman脈沖, 但這兩個脈沖相對于初始化時的基態Raman脈沖有?1的相位變化, 然后可以 測 得 宇 稱 信 號P隨?1的 振 蕩其 中C1代 表 了相干性. 如圖9所示, 通過擬合宇稱信號的振蕩, 得到C1=0.16±0.01 , 結合糾纏態的布居和得到糾纏態的保真度為F=(P↑?+P↓?)/2+|C1|=0.59±0.03. 該保真度已經超過糾纏的判定閾值0.5, 因此可以確認異核糾纏的存在.

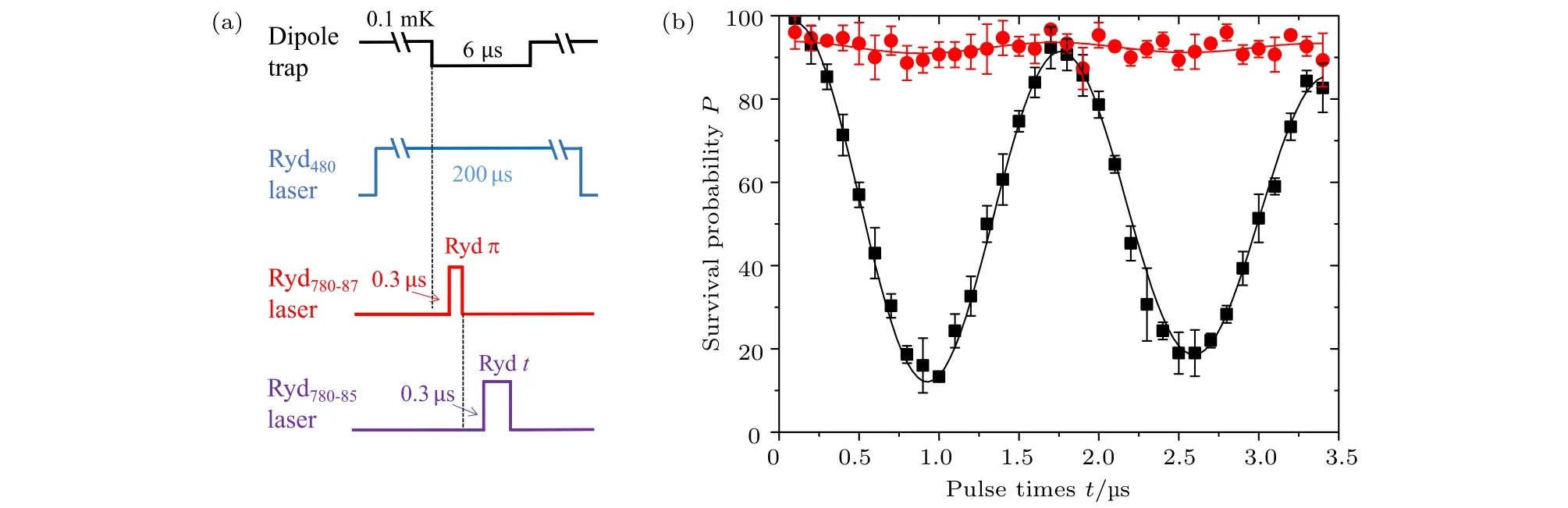
圖7 (a) 異核里德伯阻塞的時序; (b) 異核里德伯阻塞. 沒有 8 7Rb 時, 8 5Rb 展示了很好的基態到里德伯態的相干Rabi振蕩, 當87Rb激發到里德伯態時, 由于異核里德伯阻塞, 8 5Rb 幾乎沒有Rabi振蕩[20]Fig.7. (a) Time sequence for heteronuclear Rydberg blockade; (b) Rabi oscillations between the 8 5Rb 5 S1/2,F=3,mF=0 and 79D5/2,mj=5/2states with and without 8 7Rb in Rydberg state[20].

圖8 (a) 異核C?NOT門的時序; (b) 不同輸入態 | ↓ ?〉 (黑色方塊)和 | ↑ ?〉 (紅色圓點)時, 輸出態的布居隨兩個Raman π /2 脈沖的振蕩; 用正弦函數擬合后, 兩個振蕩間的相位差為 ( 0.94 ± 0.01)π ; (c) 初態制備的真值表; (d) 兩個Raman π /2 脈沖的相對相位設為0時, 測得的H?Cz型的C?NOT門的真值表[20]Fig.8. (a) Experimental time sequence of H?Cz C?NOT gate; (b) output states as a function of the relative phase between the Raman π /2 pulses, for the initial states | ↓ ?〉 (black squares) and | ↑ ?〉 (red circles). The solid curves are sinusoidal fits yielding the phase difference of ( 0.94 ± 0.01)π between the two signals; (c) truth table matrix for the initial state preparation; (d) set the relative phase to be 0, the measured truth table matrix for H?Cz C?NOT gate[20]..

實驗中異核兩原子糾纏的保真度主要受限于異核受控非門的保真度和原子熱運動引起的退相.在我們的實驗中, 原子的溫度約為控制量子比特的兩個里德伯 π 脈沖的時間間隔是δt=3.6 μs, 在此期間, 由于原子的熱運動累積的隨機相位為其中 k 為對射的480和780 nm里德伯激發光的波矢由此得到隨機相位對糾纏保真度的限制為結合受控非門的保真度, 糾纏保真度的上限應為0.03, 與實驗結果比較符合. 下一步實驗將優化實驗條件, 目標是降低原子的溫度到4 μ K , 并提高里德伯激發光強從而減少兩個里德伯 π 脈沖的時間間隔到1.5 μs , 從而可以將原子熱運動導致的糾纏保真度限制提高到

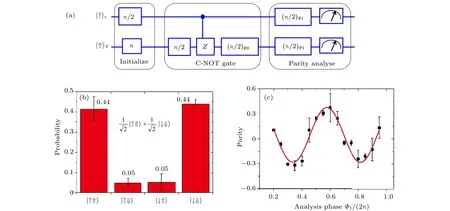
圖9 (a) 制備和測量異核兩原子糾纏的時序; (b) 糾纏態的布居; (c) 宇稱信號隨測量脈沖相對相位的振蕩, 擬合得到|C1|=0.16±0.01[20]Fig.9. (a) Time sequence for generating and verifying entanglement of two heteronuclear atoms; (b) measured probabilities for the entangled state; (c) the parity signal P ; the solid curve is a sinusoidal fit with |C 1|=0.16±0.01 [20].

5 總結與展望

在科學界持續而深入地對量子計算的實現條件、計算能力進行研究的過程中, 清晰地確定并展示量子計算機相對于傳統設備的優勢將是量子計算研究領域中一個具有里程碑意義的目標. 如“量子霸權”(quantum supremacy)[83], 認為對某些特定的問題, 并不需要量子編碼過程, 只需要50個物理量子比特量子計算機(準確地說是專為解決具體問題而構建的量子模擬器, 而不是普適的量子計算機)就可以超越現在的超級計算機的能力. 隨后這一數目的要求通過優化經典算法, 又進一步提高到64位[84]. 但單單提高量子比特數目, 而使用較差保真度的量子邏輯門, 并不會有效提高體系的量子計算能力, 因此IBM的科學家進一步提出了“量子容積”的概念. 近期, Bravyi等[85]首次證明了求解特定線性代數問題時量子算法的優勢, 并行量子電路需要的計算步驟和問題規模無關, 而類似的經典電路需要的計算步數隨著問題規模的增長而對數式增加. 由此可見, 明確量子計算相對于傳統設備的優勢, 針對現有傳統計算難以克服的問題提出新的量子計算的優勢方案將是未來量子計算理論方面的主要研究內容. 而在實驗上, 提高物理量子比特的數目、提高邏輯門操作保真度、進而實現優化的特定目的量子算法將是下一階段量子計算實驗體系追求的主要目標.

相比于其他量子計算體系, 中性原子體系在相干時間、可控相互作用和擴展性方面都具備一定優勢, 但在邏輯門操作的保真度和量子態探測方面還存在不足. 近期, 在保真度方面, 我們研究組的單量子比特操作的保真度已突破0.9999[86]; 在兩量子比特邏輯門保真度方面, 在Levine等[82]通過高細度FP腔過濾里德伯激發光相位噪聲并實現了保真度達到0.97的兩原子糾纏態后, 通過更為嚴格和精確地操控實驗條件, 包括對背景電場和磁場的屏蔽和控制、亞微秒量級激光脈沖波形和頻率的同步精確調制技術、對偶極光光強的精確控制、激發光相位的保持等, 將非常有希望實現兩量子比特邏輯門的保真度突破0.99. 同時在態探測方面, Wu等[9]在3D陣列中實現了約160個量子比特態無損探測, 并且保真度達到0.9994, 這是目前4個量子比特以上量子計算體系中最高的態探測效率. 進一步實現糾錯操作時, 考慮到現有探測方案中熒光的串擾, 采用異核單原子陣列配合異核兩原子量子受控非門進行量子態探測的方案[67]將是一個很好的選擇. 其中異核單原子陣列可以采用現有的單原子裝載后重新排列的技術, 逐次對每種原子進行排列,對于排列完成后異核陣列中可能出現的缺陷可以再次進行成像并予以補充.

由此可見, 中性原子體系在保持自身優勢時,也有望解決自身不足, 當上述技術突破和優勢進一步集成到一套系統后, 中性單原子體系在量子計算和量子模擬方面將極具競爭力. 短期內, 中性單原子體系的研究將集中在數十個乃至一百個量子比特位的操控上, 并在某些問題上展示量子計算和量子模擬相對于經典計算體系的優越性. 此外, 多體相互作用的量子模擬、光子?原子接口等方面也是中性原子體系的重點研究方向, 如模擬自旋相互作用的伊辛(Ising)模型[87—89], 基于中性原子陣列與光學腔耦合并通過里德伯阻塞效應實現光子?原子量子邏輯門等[90—92]. 長期來看, 通用量子計算需要面對的將是成千上萬的量子比特, 由此帶來的更復雜的系統操控將是一個需要花費數年乃至數十年不斷研究的長期課題, 并且最終方案極有可能采用混合體系, 綜合各個體系的優勢并避免各自的不足, 實現可靠性、容錯性和糾錯性于一體的量子計算機, 并開展適用于量子計算機的接口及網絡技術、研究并發展量子算法和量子協議、將處于實驗室階段的關于量子系統的控制和測量技術轉化到工業化生產, 以期獲得工業上的興趣及支持來推廣發展量子系統等工作.

感謝研究組尉石、楊佳恒、曾勇、王坤鵬、劉楊洋、付卓、郭瑞軍、盛誠和莊軍等研究生的貢獻.