基于MC8051的壓力傳感器校準算法*
劉 歡, 魏榕山
(福州大學 物理與信息工程學院,福建 福州 350116)
0 引 言
壓力傳感器是現實生活中最常用的一種傳感器,其廣泛應用于各種工業控制、汽車電子、醫療設備等多種領域。但由于傳感器半導體材料的物理特性,其受溫度影響較大,會出現明顯的零點和靈敏度的漂移[1],尤其是在高溫區間出現溫漂現象更明顯,所以,必須要對壓力傳感器進行溫度補償,盡可能降低甚至消除溫漂對其的影響。
目前常用的補償方法主要是硬件電路補償和軟件算法補償兩種,硬件電路補償方法主要有在橋臂上串并聯合適的恒定電阻器的方法,橋外串并聯熱敏電阻器的方法以及雙電橋補償技術等。但用硬件電路進行校正大都存在電路復雜、調試困難、精度低、通用性差、成本高等缺點,不利于工程實際應用[2~4]。軟件算法補償主要是通過實驗的方法來確定壓力傳感器的靜態特性,將微處理器和壓力傳感器結合起來,充分利用豐富的軟件功能、結合一定的補償算法對傳感器溫度的附加誤差進行修正[5]。軟件算法補償[6~9]因其具有高精度和低成本而更多用于實際工程。
1 算法模型原理分析
根據壓力傳感器通常在高溫段會受到影響較大的特性,本文提出一種基于多項式曲線擬合和牛頓差值以及三次樣條插值的補償算法模型。在高溫段使用補償效果更好的最小二乘法曲線擬合結合三次樣條插值算法,在低常溫段則使用計算相對簡單的曲線擬合結合牛頓插值算法。
1.1 牛頓插值原理
Newton法是靠不停迭代來逼近函數方程的解,實際上是通過曲線一系列切線與x軸的交點的橫坐標來逼近曲線與x軸交點的橫坐標。
設函數f(x)在[a,b]上有定義,對于n+1個節點(xj,yj),j=0,1,…,n其中xj∈[a,b]互不相同,滿足f(xj)=yj,j=0,1,…,n,對任意x∈[a,b]由一階差商的定義
(1)
則
f(x)=f(x0)+f[x,x0](x-x0)
(2)
類似地通過求各階的差商,遞推得到
f(x)=f(x0)+f[x0,x1](x-x0)+…+f(x0,x1,x2,…,
xn)(x-x0)(x-x1)…(x-xn-1)+…
=Pn(x)+Rn(x)
(3)
Pn(x)=f(x0)+f(x0,x1)(x-x0)+…+f(x0,x1,x2,…,
xn)(x-x0)(x-x1)…(x-xn-1)
(4)
式中Pn(x)為次數不高于n的x的多項式,可以驗證Pn(xi)=f(xi)(i=0,1,…,n)。Pn(x)為過n+1個節點的f(x)的n階牛頓插值多項式。Rn(x)為插值多項式的余項。
1.2 三次樣條插值[10]
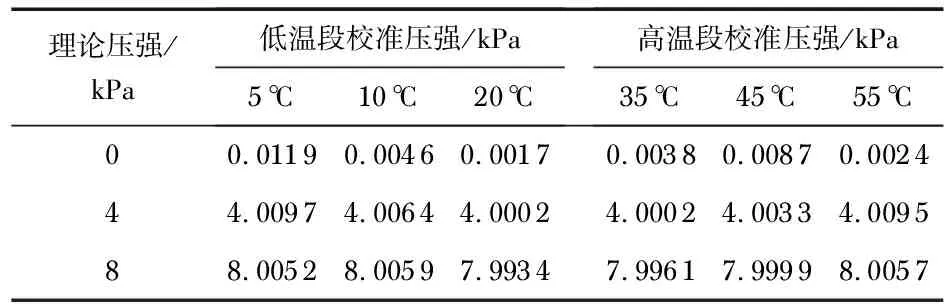
設區間[a,b]上給定一組節點X:a=x0 假定S″(xj)=Mj(j=0,1,…,n),由于S(x)在區間[xj,xj+1]上是三次多項式,所以,S″(x)在[xj,xj+1]上是線性函數,表示為 (5) 對S″(x)積分2次并利用S(xj)=yj,S(xj+1)=yj+1得 (6) 求出Mj(j=0,1,…,n)即可得到所求的三次樣條插值函數S(x)。 利用條件(3)可知,S(x)在節點xj(j=1,2,…,n-1)處應該滿足連續性條件,S(xj-0)=S(xj+0),S″(xj-0)=S′(xj+0),S″(xj-0)=S″(xj+0),再加上相應的邊界條件可得到關于Mj(j=0,1,…,n)的三對角方程組,利用追趕法可求得唯一解。 軟件補償是將微處理器和壓力傳感器結合,通過收集壓力傳感器的相關數據導入處理器,利用微處理器的處理能力,通過存儲于處理器中的補償算法對數據進行校準處理,將校準后的結果輸出。不管采用何種軟件補償方法,其硬件系統的架構是相似的,不同的地方在于算法[13]。 硬件系統架構采用自主流片的MC8051核作為中央微處理器,考慮由于ROMIP價格過于昂貴,故采用外接64 kB片外ROM,校準算法直接通過編程器燒入ROM,整體架構如圖2所示。通過在ROM中設定溫度閾值,根據壓力傳感器的當前溫度選擇相應的補償算法模型。 圖1 硬件系統結構 實驗選定一種最大量程為10 kPa的壓力傳感器,在溫度分別為0,15,30,40,50,60 ℃,壓力值0,4,8 kPa下進行標定,得到6×3組標定點。基于標定的數據點選擇合適的算法要求出溫度T,壓力p以及壓力傳感器的實際輸出電壓u三者之間的函數關系為 p=f(u,T) (7) 在不同節點i處根據對應溫度T和實際電壓輸出u計算得到的p*稱為被測校準值,其和i處實際壓力值p之間的誤差Δp=p*-p,在整個測量范圍內的最大誤差為Δpmax,則相對于傳感器滿量程pFS的綜合誤差[14]為 (8) 首先固定溫度T不變,對壓力p和輸出電壓u進行多項式擬合,得到pn=fn(u)。選定0,15,30 ℃為低常溫區間,將測得的實際電壓分別帶入第一步的線性p-U函數,從而得到不同標定溫度相對應的輸出壓力p值。對此區間溫度T和p運用二階牛頓插值算法 p=f(T0)+f(T0,T1)(T-T0)+ f(T0-T1,T2)(T-T0)(T-T1) (9) 同理,對于高溫區間30,40,50,60 ℃,對溫度T和壓力p分別運用三次樣條插值算法,因為已知p(T)滿足三次樣條插值的上述三個條件,且兩個兩端自然邊界p″(T0)=0,p″(Tn)=0,根據公式可以求得Mj(j=0,1,…,n)的值,從而得到關于溫度T的p(T)。壓力p也是根據第一步曲線擬合函數,由傳感器實際輸出電壓u得到,所以綜合最小二乘法曲線擬合函數和三次樣條插值函數即可得到關于T,u,p三者之間的關系。 根據多項式擬合最小二乘法原理,可以得到不同溫度T下的pn=fn(u),曲線擬合函數通過在MATLAB中編程實現。根據標定的數據點在圖2的分布可以看出壓力和傳感器輸出電壓呈線性關系。 圖2 不同溫度下傳感器輸出特性 由標定的數據根據上述牛頓差值和三次樣條差值原理可求得各項系數,最終得到p,T,u三者之間的函數關系表達式,即建立了補償算法模型。 對建立的溫度補償算法模型進行驗證,低常溫段選定3個溫度點5,10,20 ℃進行測試,高溫段選定35,45,55 ℃進行測試。收集輸出電壓代入補償算法模型做溫度補償,得到補償結果。最終兩溫段校準結果如表1所示。 表1 兩溫段補償校準結果 對比標準壓強和經過補償算法校準后的壓強可以發現,低常溫段測試結果的最大誤差為0.048 5 kPa,相對于傳感器滿量程的綜合誤差為 高溫段的測試結果最大誤差為0.009 5 kPa,相對于傳感器滿量程的綜合誤差為 根據一種實際壓力傳感器,基于最小二乘法擬合和牛頓差值以及三次樣條插值算法,設計了一種有效消除溫漂的校準算法,尤其適用于經常需要在相差較大的溫度下工作的壓力傳感器校準,校準誤差在0.119 %以內,且充分考慮了成本,硬件計算能力以及運行速度等問題,具有一定的實際工程應用價值。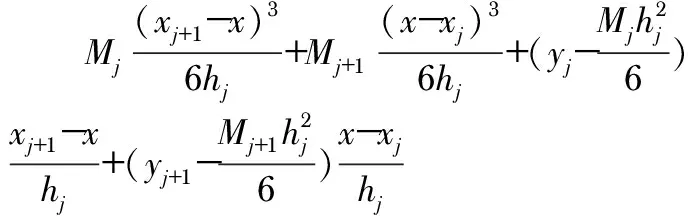
2 溫度補償算法模型及數據分析

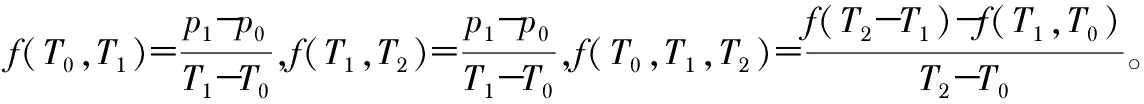

3 結 論

