滑動及側滑影響下的移動機器人軌跡跟蹤控制

衛榮慕， 金世俊

(東南大學 儀器科學與工程學院,江蘇 南京 210000)

0 引 言

近幾十年，由于移動機器人具有非完整約束的性質[1，2]，其運動控制研究具有一定挑戰性。如實際環境工作中，道路濕滑、結冰、快速轉彎等原因，移動機器人不可避免地產生側滑和滑動，破壞非完整約束[3，4]。為了解決這個問題，文獻[5]研究了運動學模型下的縱向滑動參數未知的軌跡跟蹤，設計了補償縱向滑動的自適應非線性反饋控制律，并利用極點配置在線調整控制增益。文獻[6]提出基于函數逼近技術的自適應控制方法，利用神經網絡補償干擾觀測器估計的誤差。文獻[7]設計了基于廣義擴展狀態觀測器的魯棒追蹤控制器，實現干擾的衰減和軌跡的準確跟蹤。文獻[8]提出非線性擾動觀測器的滑膜控制器，利用運動學模型導出的偏移模型設計出控制器。文獻[9]設計了自適應抗干擾控制器，將滑動和側滑以及其他擾動視作系統的整體擾動，設計出自適應律，實現機器人軌跡跟蹤。但上述文獻中的控制設計需要精確的機器人控制模型，且文獻[5，8]只考慮到運動學部分，這在移動機器人的工程實際中往往不易實現。

針對上述問題，本文提出了基于動力學的自適應模糊控制方法來解決動力學部分所受到的滑動和側滑影響。結合H∞控制理論，引用魯棒補償項[10]將建模誤差，外部干擾包括滑動和側滑衰減到預先規定的指標，通過Lyapunov方法給出了自適應律。運動學部分是通過逆運動學方法[11]設計的逆運動學控制器，處理受滑動和側滑影響的實際位置與期望位置的誤差，最后以仿真驗證了在滑動及側滑影響下，移動機器人能夠準確快速跟蹤期望軌跡。

1 數學模型的建立

本文研究的對象為差分驅動輪式移動機器人，結構如圖1所示。輪式移動機器人的動力學模型為[6]

(1)

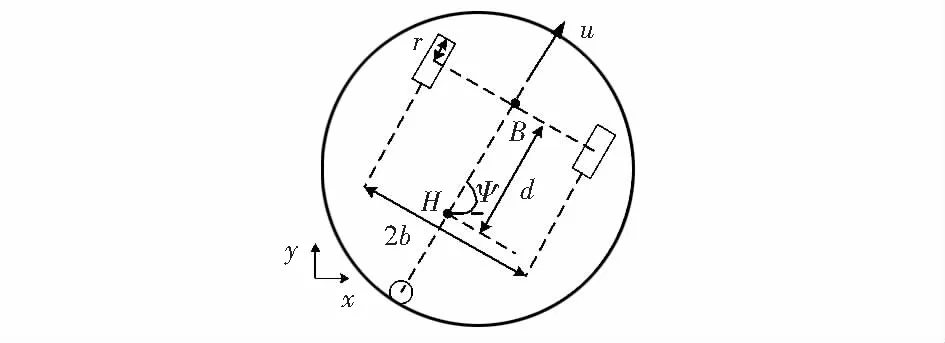
圖1 輪式移動機器人結構

由于地面的濕滑和快速轉彎，移動機器人容易發生滑動和側滑，故很難滿足理想的非完整性約束條件[11]。因此在發生滑動或側滑影響下的非完整約束條件為

(2)

式中μ為側滑速度，ζ=[ζrζl]T為左右驅動輪的滑動引起的干擾角速度。

整理式(2)可知移動機器人在滑動和側滑影響下的運行速度為

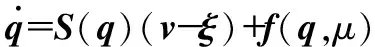
(3)

式中v=[uω]T，u為移動機器人前進的線速度，ω為移動機器人角速度,ξ=[ξuξω]，ξu為縱向滑移速度，ξω為偏航角速度。f(q,μ)為擾動非完整約束引起的不匹配干擾向量。

由式(1)和式(2)可知受滑動和側滑影響的動力學模型

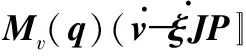
F2(q)f(q,μ)=τ+τd

(4)

式中Mv=(STB)-1STMS，Cv=(STB)-1ST(M+CS)，F1=(STB)-1STM，F2=(STB)-1STC。

定理1將輸入擾動和移動機器人的滑動、側滑均視為擾動

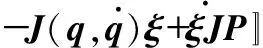
(5)

移動機器人的動力學模型可以整理為

(6)

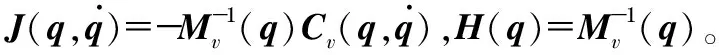
2 逆運動學控制器和自適應模糊動力學控制器設計

2.1 逆運動學控制器設計

逆運動學控制器[11]處理移動機器人實際位置與期望位置之間的誤差，輸出控制移動機器人運動的期望速度。

令輪式移動機器人的位置坐標為h=[x,y]T,則=Qv,其中

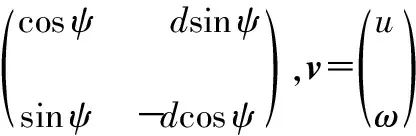
(7)

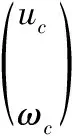
(8)

式中 [uc,ωc]T為運動學模型的期望速度，Ix，Iy為飽和常數，坐標誤差增益kx>0,ky>0。

2.2 自適應模糊動力學控制器設計

本文提出基于動力學的自適應模糊方法[2]控制器，不需要辨識或估計動態模型參數。

受滑動和側滑影響的移動機器人動力學模型可以寫為

(9)

式中z為狀態向量，k為輸入向量，ε為擾動量，P(z)和Γ(z)為模糊近似函數。

如圖2，設計自適應模糊控制器的目的是發現輸入力矩τ(t)控制實際速度v(t)漸近收斂到期望速度vc(t)。

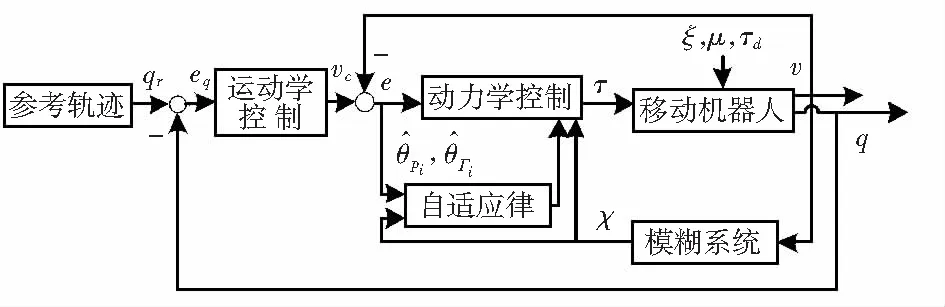
圖2 控制算法結構

動力學誤差為

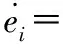
(10)

模糊系統

(11)

為設計未知參數ksi,Pi,Γi的自適應更新率。設計李雅普諾夫函數為

(12)

式中φi,γP,γΓ為正數。

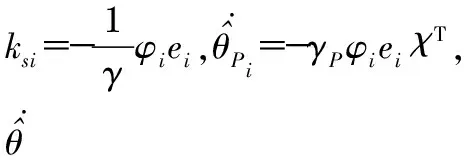
(13)

假設φi滿足

(14)

式中ρ,γ,η為正數,則

(15)

此外必須滿足式(16)保證式(14)的一個解φi為正數

(16)

不等式(15)是H∞指數[10]，因此利用控制律和自適應律可以保證(vc-v)→0。

2.3 完整控制系統穩定性證明

將運動學部分和動力學部分級聯后，運動學部分變為

(17)

式中δ為速度控制偏差造成的系統位置控制的偏差

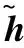
(18)

3 仿真分析

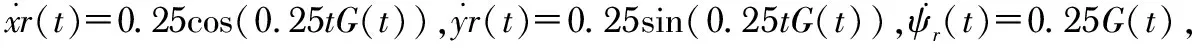
設輪式移動機器人初始姿態(x,y,4)為(0.5,0.5,0)。選取運動學控制器的參數為kx=ky為1，lx=ly為0.1。選取動力學控制器的參數為γ為0.1，γΓ為0.09，γP為0.9，φ1為10，φ2為5，α1為0.1，α2為1。擾動量[ζrζlμ]T和τd分別為[sin(t) cos(t)F(t)]T和[2sin(t) 2cos(t)]T。其中,F(t)=20[U(t-21)-U(t-23)]+24[U(t-37)-U(t-39)]為側滑量，U(t)為單位階躍函數。

利用MATLAB/SIMULINK進行仿真分析，將本文提出的自適應模糊動力學控制器與文獻[9]自適應控制方法動力學控制器進行對比。

1)由圖3(a)可知移動機器在沒發生側滑，只受滑動影響時，能夠準確跟蹤軌跡。在前兩個轉彎處同時受滑動和側滑影響時能夠迅速恢復行駛到期望軌跡上。由圖3(b)可知在前兩個轉彎處受滑動和側滑影響下，軌跡跟蹤誤差較大，且不能迅速恢復軌跡跟蹤。在第三個轉彎處只有滑動存在，也不能準確進行軌跡跟蹤。

圖3 軌跡跟蹤對比

2)從圖4可知，在21～23 s和37～39 s時受側滑影響，2種方法控制的軌跡跟蹤誤差都變大，但是自適應模糊控制的軌跡跟蹤誤差較小，且能夠迅速跟蹤到期望軌跡上。

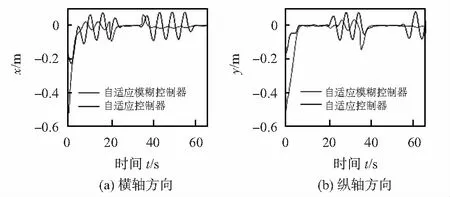
圖4 不同方向軌跡跟蹤誤差

3)從圖5可知，自適應模糊控制在發生側滑時，機器人線速度和角速度跟蹤誤差較大，但側滑因素消失后，兩速度跟蹤誤差漸近于零。而自適應控制在沒有側滑影響時也出現周期性誤差。

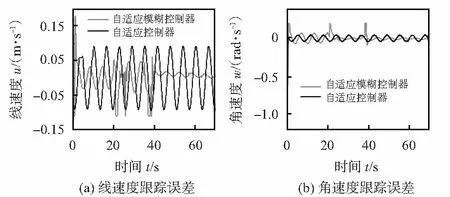
圖5 速度跟蹤誤差比較

4 結 論

1)根據移動機器人受滑動及側滑影響下的非完整性約束條件，構造出移動機器人的動力學模型。并推導出新的控制系統狀態方程。在運動學部分，設計逆運動學控制器，得到移動機器人的期望速度。

2)提出了在滑動和側滑影響下，基于動力學的自適應模糊控制。通過模糊系統逼近動力學控制系統的未知非線性，H∞對滑動和側滑干擾的補償，設計出模糊系數的自適應律，解決移動機器人偏離期望軌跡的問題。

3)仿真表明：本文所提方法有效補償了滑動和側滑引起的擾動，使移動機器人在滑動和側滑的影響下，能夠有效進行軌跡跟蹤。