采動應力下煤體滲透率模型構建及研究進展
周宏偉,榮騰龍,牟瑞勇,王路軍,任偉光
(1.中國礦業大學(北京) 能源與礦業學院,北京 100083; 2.中國礦業大學(北京) 力學與建筑工程學院,北京 100083; 3.中國礦業大學(北京) 煤炭資源與安全開采國家重點實驗室,北京 100083)
煤炭是我國的基礎能源,也是重要的工業原料,到2030年,煤炭科學開采預測產能總量達30~35億t[1]。所以,未來一段時間內煤炭生產仍將持續進行,煤礦的安全生產仍需加強保障。煤炭形成過程中伴生有大量的瓦斯氣體,瓦斯既是瓦斯爆炸、煤與瓦斯突出災害的誘因,又是一種高效的清潔能源[2-4]。掌握煤層中瓦斯流動規律是減少瓦斯事故、擴大瓦斯采集利用的前提,而煤體的滲透率是決定瓦斯流動規律的關鍵參數[5],所以對煤體滲透率進行研究是十分必要的。我國大部分礦區的煤層滲透率較低,需通過采動卸壓、水力壓裂、深孔爆破等手段進行人工增透[6-8],此外煤與瓦斯突出事故多發于掘進工作面[9-11]。因此,建立工作面前方采動應力下的煤體滲透率模型對提高瓦斯抽采和減少瓦斯事故具有重要意義。
以往的煤體滲透率模型較多以煤層氣開采為背景[12-14],同時基于單軸應變條件和上覆載荷不變的假設建立,而在煤礦采掘活動中,煤層的受力特點有別于煤層氣開采。工作面推進過程中采煤工作面前方煤體經受采動應力路徑的變化過程,其豎直方向的支承壓力逐漸升高后下降、水平方向的應力持續降低,煤層受力呈現典型的三向應力變化特征(圖1(a))。隨著支承壓力的升高以及人工增透活動的進行,煤體內部繼發出現損傷和破裂現象,煤層內裂隙擴展貫通造成瓦斯壓力下降,同時伴隨瓦斯解吸擴散的發生,最終煤體滲透率急劇增長。采動應力決定了煤體在由原巖應力狀態漸近為側面臨空過程中的受力狀態、物理力學特征、溫度梯度及滲透率變化有別于煤層氣的抽采過程,以往的煤體滲透率模型并不能完全適用于采動應力條件。
筆者首先概述了煤體滲透率經典模型,然后結合采動過程中煤體內的力學變化機制及滲透率的控制因素提出了采動應力下煤體滲透模型構建中的3個關鍵問題,即采動煤體各向異性特征、采動煤體損傷破裂特征和煤體吸附解吸特征,并將這3個方面的國內外研究成果進行了總結和分析。在此基礎上,將各向異性特征的煤體滲透率模型歸納為由有效應力變化表征和幾何參數變化表征的兩類,又將損傷破裂特征的煤體滲透率模型劃分為本構方程中含損傷變量和滲透率表達式中含損傷變量的兩類。最后,對采動應力下煤體滲透率模型的研究進展進行了介紹并對當前采動應力下煤體滲透率模型研究的不足和未來的發展方向進行了探討。
1 煤體滲透率經典模型概述
為了對煤體的滲透率演化過程進行定量描述,國內外學者建立了大量的滲透率模型,這些研究成果主要集中在煤層氣開采方面,其中一些模型具有較高的代表性,這些經典的模型成果在煤體滲透率模型的研究領域中發揮了重要作用。
GRAY[15]認為煤儲層的滲透率與垂直于割理結構的有效水平應力大小有直接關系,較早建立了煤體滲透率演化模型。SEIDLE等[16]將儲層煤體簡化為“捆綁的火柴棍”幾何結構,得到了煤體滲透率與有效靜水壓力的關系,從理論角度推導出滲透率變化的指數函數形式。PALMER和MANSOORI[17]假設儲層為單軸應變條件,考慮煤層割理壓縮性的變化,基于滲透率k與孔隙率φ的立方關系,結合非等溫多孔彈性理論建立了煤層滲透率模型。SHI和DURUCAN[18]從各向同性的彈性本構方程出發,將煤儲層視為連續介質,基于單軸應變的假設條件求出煤儲層水平方向有效應力的變化,建立了指數函數形式的滲透率模型。CUI和BUSTIN[19]考慮整體平均有效應力對煤體孔隙度和滲透率的影響,利用多孔彈性本構方程進行推導得到解吸過程中煤體滲透率模型。ZHANG等[20]將煤體視為固體顆粒和孔隙空間組成,假設煤的孔隙空間同樣存在吸附應變,建立了一個廣義孔隙度的滲透率模型。LIU等[21]認為煤體滲透率由基質滲透率和裂隙滲透率2部分組成,考慮基質和裂隙的相互作用得到合成的滲透率表達式。經典的煤體滲透率模型匯總見表1。
表1煤體滲透率經典模型
Table1Classicalpermeabilitymodelsofcoals

文獻來源模型表達式參數釋義GRAY[15]σeh-σeh0=-ν1-ν(p-p0)+E(1-ν)ΔεsΔpsΔpsk=1.013×10-0.31σehσeh為水平有效應力;ν為泊松比;E為彈性模量;p為氣體壓力;Δεs/Δps為單位等效吸附壓力改變下的煤體應變;Δps為等效吸附壓力變化增量;k為煤的滲透率;下標0為初始狀態SEIDLE等[16]kk0=exp[-3Cf(σehy-σehy0)]Cf為割理壓縮系數;σehy為有效的靜水壓力PALMER和MANSOORI[17]φφ0=1+cmφ0(p-p0)+clφ0KM-1 Bp1+Bp-Bp01+Bp0 kk0=φφ0 3M=E(1-ν)(1+ν)(1-2ν),K=E3(1-2ν),cm=1M-KM+G-1 γs,其中γs為顆粒壓縮系數;φ為孔隙率;cl為Langmuir吸附應變常數;B為Langmuir吸附平衡常數;G為比例系數SHI和DURUCAN[18]σeh-σeh0=-ν1-ν(p-p0)+E3(1-ν)εLpp+pL-p0p0+pL kk0=exp[-3Cf(σeh-σeh0)]εL為Langmuir吸附體積應變常數;pL為Langmuir吸附壓力常數CUI和BUSTIN[19]kk0=exp-3Kp[(σm-σm0)-(p-p0)] Kp為孔隙體積模量;σm為平均法向應力ZHANG等[20]kk0=11+S(1+S0)+αbφ0(S-S0) ? 3S=εV+(p/Ks)-εs,S0=(p0/Ks)-εLp0/(p0+pL),αb=1-K/Ks,Ks為煤固體顆粒體積模量;K為煤的體積模量;εV為煤的總體積應變;εs為煤的吸附應變LIU等[21]kk0=km0km0+kf01+Rmpmφm0K 3+kf0km0+kf01+1-Rmφf0(ΔεV-Δεs) ?3km為基質滲透率;kf為裂隙滲透率;φm為基質孔隙率;φf為裂隙孔隙率;Rm為整體彈性模量損失率;pm為基質上的氣體壓力
2 采動應力下煤體滲透率模型構建的關鍵問題
2.1 采動煤體各向異性特征
煤屬于沉積巖,在沉積方向具有明顯的層理結構,而在垂直層理的方向又存在空間狹窄的裂隙結構,這種結構被稱為割理結構。割理可分為面割理和端割理結構,通常將兩種割理結構簡化為相互正交的形式。因此,煤體具有顯著的各向異性特征(圖1(b)),進而煤體在各個方向上存在不同的滲透率變化趨勢。除此之外,采動應力下煤體滲透率模型的構建必須把握三向受力的特點,建立可表征豎向加卸載、水平卸載過程的滲透率理論模型。因此,無論是煤體內部結構特征還是外部受力條件均要求使用各向異性的滲透率模型對采動應力下煤體的滲透率演化過程進行描述。筆者根據滲透率模型的建模角度將現有的各向異性煤體滲透率模型成果歸納為有效應力變化和幾何參數變化兩類進行介紹。各向異性特征的煤體滲透率模型匯總見表2。
表2各向異性滲透率模型
Table2Anisotropicpermeabilitymodels

文獻來源模型表達式參數釋義CHEN等[22]ki=ki0exp[3Cfi(σei-σei0)] i=x,yCfi為不同方向的割理壓縮系數;σei為不同方向的有效應力LIU等[23]ki=ki0exp[-3Cfi(σem-σem0)] i=x,y,zCfi為不同方向的平均割理壓縮系數;σem為有效的平均法向應力ZHANG等[24]ki=ki0exp[-αiCpσ(σi-σi0)] i=x,y,zCpσ為孔隙壓縮系數;αi為冪函數系數;σi為不同方向的應力PAN和CONNELL[25]ki=ki0exp[3Cfi(σei-σei0)] i=x,y—GU和CHALATURNYK[26]kiki0=1+ajbjΔεfj 31-Δεfj i=x,yaj為j方向的基質單元寬度;bj為j方向的裂隙單元寬度;Δεfj為j方向的裂隙應變增量馬天然等[27]ki=∑3j=1(bj0+Δbj)312(aj0+Δaj) i=x,y,z—LIU等[28]kiki0=∑i≠j121+3(1-Rm)φf0(Δεtj-13Δεs) ?Δεtj為j方向煤體的總應變YANG等[29-31]kxkx0=121+3(1-R2)φ0 ?(Δεt2-13Δεs) 3+ 121+3(1-R3)φ0 ?(Δεt3-13Δεs) 3kyky0=121+3(1-R1)φ0 ?(Δεt1-13Δεs) 3+ 121+3(1-R3)φ0 ?(Δεt3-13Δεs) 3kzkz0=121+3(1-R1)φ0 ?(Δεt1-13Δεs) 3+ 121+3(1-R2)φ0 ?(Δεt2-13Δεs) 3Ri為i方向的模量損失率;Δεti為i方向的煤體總應變WANG等[32]kiki0=1+2(1-Rm)φf0Δεej ?3 i,j=x,y,z;i≠jΔεej為j方向的煤體有效體積應變WU等[33]kmkm0=1(1+S)φm0[(1+S0)φm0+αb(S-S0)] 3kiki0=∑i≠j121-1φf0+3KfK13αTΔT+13Δεs-1KΔσei ?3Kf為裂隙剛度;αT為熱膨脹系數;T為溫度WANG等[34]ki=ki0 1+1φi0Δσej-vbjkΔσek-vbijΔσeiEbj-Δσej-vmjkΔσek-vmijΔσeiEmj+Δσek-vbkiΔσei-vbjkΔσejEbk-Δσek-vmkiΔσei-vmjkΔσeiEmk-εLjFljppLj+p-Fljp0pLj+p0 -εLkFlkppLk+p-Flk0p0pLk+p0 ? 3i≠j≠kEbi為i方向的煤體彈性模量;Emi為i方向的基質彈性模量;εLi為i方向的Langmuir吸附體積應變常數;pLi為i方向的Langmuir吸附壓力常數;Fli為i方向的內膨脹應變系數
2.1.1 有效應力變化表征的煤體滲透率模型
有效應力變化表征的煤體滲透率模型都以煤體所受有效應力為自變量,在建模過程中較多將煤基質和裂隙視為一個整體,利用彈性本構方程對煤體在坐標軸3個方向的應力和應變關系進行推導,建立滲透率和有效應力之間的關系。此類模型[22-25]均可以歸納為以下形式
(1)
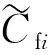
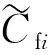
(2)
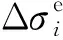
2.1.2 幾何參數變化表征的煤體滲透率模型
幾何參數變化表征的煤體滲透率模型大多以煤體內孔裂隙尺寸、裂隙應變和孔隙度為自變量,建模過程基本是將煤體劃分為基質和裂隙兩部分,通過計算應力、吸附作用下裂隙尺寸或孔隙度變化,建立煤體裂隙開度、孔隙度和滲透率的關系。為了考慮煤體各向異性的結構特征(圖1(b)),這些滲透率模型[26-34]構建過程中大多將煤體抽象為立方體幾何結構模型(圖1(c))。
一些學者將氣體在煤層裂隙中的流動簡化為平板間流體流動過程,通過POISEUILLE定律得到滲透率與裂隙開度之間的立方關系(式(3)),并以此開始推導,即
(3)
式中,a,b分別為基質單元和裂隙單元的寬度。
GU和CHALATURNYK[26]將煤體簡化為火柴棍模型,而馬天然等[27]將煤體簡化為立方體模型,分別對式(4)進行變換直接得到了滲透率和裂隙開度的3次方關系式。LIU等[28]將煤體抽象為立方體幾何結構,認為煤體為各向同性的線彈性材料,提出了模量損失率來表征各方向彈性模量的變化過程,建立了不同邊界條件下的各向異性滲透率模型。YANG等[29-31]認為工程分析中應忽略基質滲透率的影響,借此對LIU等[28]模型加以修正,構建出橫觀各向同性的滲透率模型。WANG等[32]從式(4)出發對壓縮過程中裂隙孔徑的變化進行推導,得出一個與LIU等[28]模型形式類似的表達式,同時定義了基質與整體單元應變比的新參數,建立了一個2維各向異性的滲透率模型。
另外,一些學者定量表示出三向有效應力變化過程中煤體內部孔隙度的變化,并將孔隙度變化結果代入滲透率和孔隙度的立方關系[17](式(4))建立了相應的各向異性滲透率模型。WU等[33]將煤體的物理力學性質視為各向同性,假設坐標軸3個方向下熱膨脹和吸附作用產生的煤體應變相等而有效應力不相等,建立了雙孔隙度的煤體各向異性滲透率模型。WANG等[34]基于立方體模型提出了內膨脹應變系數以對吸附過程中煤體基質的內膨脹量進行修正,建立了一個以三向有效應力和氣體壓力為自變量的滲透率模型。
(4)
式中,k為滲透率;φ為孔隙率。
從建模過程上來說,有效應力變化和幾何參數變化的兩個建模角度可認為是互逆的相反過程。有效應力的角度是將煤體所受有效應力通過孔隙度、應變、模量、泊松比、吸附常數等參數綜合表示出來,而幾何參數的角度是將裂隙開度或孔隙度用應力、模量、泊松比、吸附常數等參數進行表達,進而各自代入相應的框架基礎公式。此外,根據各自建模所依據的框架基礎,有效應力角度建模結果基本為指數型函數、幾何參數角度建模的結果多數為3次方的冪函數。
滲透率模型中如果能將煤體的邊界條件和結構參數均考慮為各向異性且持續變化的特征是最為理想和貼近實際的情況,然而受目前試驗條件和測試手段所限,大量學者也只能將模型中的部分參數做出近似和假設處理。從上述各向異性的模型成果中可以看出,外部邊界的三向應力和三向應變參數較易跟蹤和獲取,所以三向應力的特征在模型中容易實現[22-25]。結構異性參數大多較難準確把握,比如3個方向的割理壓縮系數、彈性模量和泊松比等,因此一些模型中將結構參數視為各向同性[26-33]。
2.2 采動煤體損傷破裂特征
受開采擾動的影響,支承壓力的空間分布具有分區化特征,煤體由原巖應力逐漸升高至應力峰值后迅速卸壓(圖1(a)),在此過程中煤體由原生初始狀態漸進為損傷破裂狀態,伴隨煤體內微裂紋的擴展貫通,滲透率將會迅速增大,可達初始值的數十倍,乃至百倍[35-36]。因此,對于采場前方煤體必須考慮開采擾動引起的損傷破裂對滲透率的影響。
目前,國內外學者已經開始探究損傷破裂影響下滲透率的變化規律。開采擾動下煤體中瓦斯流動及滲透率的變化是一個典型的氣固耦合問題。一種解決此問題的手段就是將應力場和滲流場的控制方程進行耦合求解。根據損傷力學理論可以定義多種形式的損傷變量,損傷變量對滲透率的控制作用通過耦合方程的形式進行傳遞。這種調控方式下,損傷變量處于固體力學的本構方程之中,而滲透率表達式內并不含損傷變量。另一種處理此問題的方式就是將定義出的損傷變量直接嵌入滲透率模型的表達式之中。筆者依據損傷變量所處的位置不同將損傷特征的實現方式歸納為兩種:一種為損傷變量存在于本構方程中,另一種為損傷變量存在于滲透率表達式中。考慮損傷破裂特征的滲透率模型成果匯總見表3。
表3考慮損傷破裂特征的滲透率模型
Table3Damage-basedpermeabilitymodels

文獻來源模型表達式參數釋義YANG等[48]k=k0e-β1(σ1-α1p) D=0ξk0e-β1(σ1-α1p) D>0 k=k0e-β1(σ3-α1p) D=0ξk0e-β1(σ3-α1p) 0 2.2.1 本構方程中含損傷變量的煤體滲透率模型 一些學者基于宏觀唯象的連續損傷力學理論建立了煤體損傷本構并將其代入固體力學控制方程,與瓦斯滲流方程聯立進行求解。基于LEMAITRE[37]提出的應變等效假設(式(5)),魏明堯等[38]建立了彈塑性損傷本構;HU等[39]定義了雙重孔隙結構下煤體的等效彈性損傷柔度張量,構建了雙重孔隙介質損傷的本構模型;WANG等[40-41]將HU[39]定義的等效彈性損傷柔度張量進行簡化后應用在單一孔隙率的滲流方程之中,即 (5) 另外,一部分學者通過細觀損傷力學的方法建立了煤體的損傷本構,將煤體視為大量代表性體積單元(RVE)組成,通過研究每個RVE的力學破壞特征來反映煤體內損傷演化過程。ZHU和TANG[42-43]考慮巖石的非均質性,假設巖石參數符合Weibull分布(式(6)),將最大拉應力和Mohr-Coulomb準則作為判斷煤體RVE破壞的準則(式(7)),建立了煤體的彈性損傷本構。沿用這種研究思路,一些學者建立了不同的氣固耦合模型用以探究煤層中損傷-應力-滲流的問題,間接搭建了損傷變量和滲透率之間的關系[44-52]。除了根據滲透率與孔隙度立方關系(式(4))推導滲透率表達式的常見方法[44-45]之外,YANG等[48]利用分段函數依次建立了煤體單元在壓縮和拉伸條件下的滲透率函數式;劉力源等[51-52]將煤體視為雙重孔隙介質,結合煤體吸附CO2出現的損傷演化過程分別得到煤基質和裂隙的滲透率計算式。 (6) 式中,C1,C2為兩個損傷破裂閾值函數;u為單元參數;u0為單元參數的平均值;m為函數的形狀參數;σ1,σ3分別為單元的最大主應力和最小主應力;ft0為單軸抗拉強度;fc0為單軸抗壓強度;φ′為內摩擦角。 2.2.2 滲透率表達式中含損傷變量的煤體滲透率模型 通過理論推導構建損傷變量并將其嵌入滲透率表達式的研究主要限于連續損傷力學的框架內進行,大多數學者基于應變等效假設展開研究,而損傷變量的構建方法多樣。XUE等[53]通過孔隙度和有效應力定義了損傷變量;ZHANG等[54]采用煤體的體積應變、吸附應變和初始孔隙率構建了損傷變量;LI等[55]以軸向應變構建了損傷變量。另外,也有學者采用回歸分析的方法,通過擬合系數來確定滲透率和不同損傷程度下應力狀態之間的關系。CHEN等[56]為了描述煤體從彈性狀態到峰后破壞的滲透率變化全過程,提出了修正系數L,通過回歸函數得到有效偏應力與修正系數L的“S”形關系。ZHANG等[57]基于達西定律和裂隙的本構方程,通過擬牛頓算法的回歸分析確定了以應力表示的滲透率函數。為了搭建滲透率和損傷變量之間的“橋梁”,另外一些學者立足于試驗結果反映出的變化規律,在前人建立的滲透率模型基礎之上進行改造,直接添加反映損傷影響的作用項或修正系數對滲透率變化過程進行推演,也取得了一些研究成果。ZHU等[58]在滲透率和孔隙度的立方關系(式(4))上進行改造,添加了指數形式的損傷作用項;ZHENG等[59]以CUI和BUSTIN[19]模型為基礎,在該模型中添加了損傷作用項,假設了滲透率和損傷變量的指數關系;XUE等[60]通過室內試驗的滲透率和聲發射數據反分析提出在峰后階段引入一個作用項來反映損傷影響,并假設峰后階段滲透率和損傷變量呈線性關系;XIE等[61]假設損傷作用下滲透率的變化符合式(8)的關系,即 (8) 式中,ζ為與材料有關的系數。 可以看出,考慮損傷破裂特征的滲透率模型研究在近十年才逐漸展開,該領域的研究尚處于起始階段,模型中損傷效應的研究深度尚淺,損傷變量的構建方式也較為分散。在模型適用性上,損傷變量存在本構方程中的實現方式可以適用較多邊界條件情況,具有更廣的適用范圍,但是該方式下求解煤體滲透率需要依次計算應力場和滲流場控制方程,計算工作量較大,所以該方式更適合采用數值計算。損傷變量存在滲透率表達式的實現方式使得研究滲透率與各因素之間的數量關系更加便捷,但其大多基于已有模型成果進行改進,受原模型構建過程中的假設條件限制,諸如單軸應變條件、上覆載荷不變等。損傷變量所處不同位置的兩種處理方式都可以達到在滲透率計算過程中考慮損傷破裂影響的目的。究其本質而言,損傷變量存在于本構方程的情況可視為損傷變量存在滲透率表達式情況的隱式函數形式。 不同于其他氣體在巖石中的滲透行為,瓦斯在煤層中運移時存在吸附解吸的特殊現象。煤層采掘過程中,煤體損傷破裂伴隨著瓦斯滲流通道的形成。與此同時,開采擾動打破了煤層內原有的瓦斯壓力平衡狀態造成瓦斯壓力持續下降,煤體內吸附態瓦斯釋放引起解吸現象的發生。吸附解吸作用直接影響煤基質的脹縮變形,在滲透率模型構建的過程中,大多通過吸附應變這一中間變量間接反映煤體所受有效應力的大小或煤體內部滲流通道幾何尺寸的變化[62],因此關于吸附應變的計算方法就成為了研究吸附解吸影響下滲透率變化的焦點。 在早期的煤體滲透率模型中,通常將吸附應變與氣體壓力的增量視為線性關系進行處理。GRAY[15]通過提出等效吸附壓力的概念建立了吸附應變與氣體壓力之間的線性關系。LEVINE[63]利用基質收縮系數確定了基質吸附應變和氣體壓力增量之間的線性函數。國內外學者普遍將煤對瓦斯的吸附認為是物理吸附過程且為單分子層吸附。基于此,Langmuir等溫吸附模型[64]可以較好的用于煤對瓦斯氣體吸附量的計算(式(9))。HARPALANI和CHEN[65-66]認為在氣體吸附過程中吸附應變和氣體吸附量成正比,采用Langmuir理論公式計算瓦斯氣體吸附量,建立了煤體吸附應變和瓦斯氣體吸附量的線性關系(式(10))。鑒于Langmuir等溫吸附模型可以較好的描述氣體壓力改變下煤對瓦斯的吸附氣體量,LEVINE[63]對Langmuir模型作出進一步改進,采用一個和Langmuir吸附模型具有相同數學函數形式的方程(式(11))來描述煤體吸附應變。 εs=αsVs(10) 式中,Vs為吸附的瓦斯氣體含量;VL為Langmuir體積常數;αs為煤的吸附膨脹系數;εL為Langmuir吸附體積應變常數;pL為Langmuir吸附壓力常數。 煤體對瓦斯吸附解吸的內在機理可通過熱力學理論進行探究,所以除了采用上述Langmuir形式的方程對吸附應變進行表征之外,一些學者通過吸附熱力學方法建立了吸附應變的計算式[67-72],詳見表4。 表4吸附熱力學角度建立的吸附應變表達式 文獻來源吸附應變表達式參數釋義PAN和CONNELL[67]εs=RTAln(1+Bp)ρmEmf(x,νm)-pEm(1-2νm)R為氣體常數;T為溫度;A為Langmuir吸附常數;ρm為煤基質密度;Em為基質的彈性模量;νm為基質的泊松比LIU和HARPALANI[68]εl=3AρmRTEAVg∫p0B1+Bpdpεl為吸附/解吸引起的線性應變;EA為吸附解吸的膨脹模量;Vg為氣體摩爾體積LIU等[69]εs=nsatRTVcEc[ln(1+Bpt)-ln(1+Bpr)]nsat為飽和吸附摩爾數;Vc為煤的體積;Ec為煤的彈性模量;pr為起始氣體壓力;pt為終止氣體壓力VERMOREL和PIJAUDIER-CABOT[70]εs-εs0=∫pp0dpK1-KKs (1-χ)-1-1 ?χ為約束度HOL等[71]εsij=Vm0ρ(Aij+δij)3Cσεsij為各個方向的吸附應變;Vm0為吸附相的偏摩爾體積;ρ為煤的密度;Aij為各向異性膨脹張量;δij為克羅內克符號;Cσ為吸附分子的摩爾數 采用以氣體壓力增量為自變量的線性函數對煤吸附應變進行描述是最早的研究方法,其優點是瓦斯氣體壓力的測定較為簡單,但是線性函數卻有夸大瓦斯壓力對吸附應變影響的缺點。通過對比試驗結果發現Langmuir等溫吸附理論可以很好的描述煤對瓦斯的吸附解吸過程,上述Langmuir形式的吸附應變表達式具有一定的理論基礎且方程形式較為簡潔,表達式中的VL,εL,pL等參數也較易測試,所以式(10)[73-76]和式(11)[77-80]被后來學者大量效仿使用。通過熱力學方法建立的吸附應變大多以吸附熱力學為基礎進行推導,由此得出的吸附應變表達式具有更為嚴密的理論基礎,然而此類方法的模型參數較多且部分參數難以準確測定,所以此類吸附應變表達式的實用性有所限制。 現有的煤體滲透率模型中同時考慮各向異性、損傷破裂、吸附解吸等特征的滲透率模型還較少。近些年,部分學者已經開始關注這一問題,并建立了相應的采動應力下煤體滲透率模型。筆者將這些模型成果歸納為有效應力型、幾何參數型和系數擬合型的3種進行介紹。 有效應力型的煤體滲透率模型主要以有效應力、氣體壓力、彈性模量和泊松比等力學參數為基本變量對滲透率的變化進行表征。其中,ZHANG等[81]基于立方體模型結構(圖1(c)),運用損傷和斷裂力學理論提出了一個可考慮采動應力引起微裂紋擴展、吸附解吸造成煤體變形的有效應力型滲透率模型(式(12)),并根據謝和平等[82]提出的3種典型開采方式下采動應力路徑(圖2),對采動煤體滲透率變化規律進行了擬合分析。 圖2(a)~(c)為不同開采方式下煤體滲透率的試驗和擬合結果。可以看出在3種開采方式下,隨著采動卸壓過程的進行,煤體內微裂隙不斷萌生和擴展,損傷積累不斷增大,滲透率的實測和擬合結果持續升高。無煤柱和放頂煤開采方式的滲透率在加卸載途中出現陡然上升的情況,但擬合結果卻沒有出現陡然升高的特征。不過整體來看,式(12)基本可以反映出煤體滲透率隨著采動卸壓過程的進行而持續升高的變化規律。 幾何參數型的煤體滲透率模型主要以孔隙率和煤體應變為基本參數來構建滲透率模型。ZHENG等[83]將LIU等[28]提出的煤體各向異性滲透率模型和ZHU等[58]定義的損傷破裂特征修正項進行聯結。通過細觀損傷力學的方法構建損傷變量以對滲透率進行修正,合成出可表征采動應力下煤體損傷的幾何參數型滲透率表達式: 圖2 不同開采方式下應力路徑及煤體滲透率演化[81-82]Fig.2 Stress paths and permeability of coal under different mining layouts[81-82] 式中,εj為j方向的應變;εt0,εc0分別為最大拉伸主應變和最大壓縮主應變;ε1,ε3分別為最大主應變和最小主應變。 其后,利用式(13)分別對考慮和不考慮損傷效應的保護層底板下煤巖體滲透率進行了模擬分析。由圖3可以看出距離保護層底板下方80 m處的巖體滲透率為初始狀態;在與底板距離縮進過程中煤巖體滲透率逐漸升高;在距離底板12 m之外,考慮損傷與否的滲透率結果相同;而在12 m范圍之內,考慮損傷效應的煤巖體滲透率比率出現急劇上升,從初始滲透率比率的180倍陡增至680倍左右,而不考慮損傷的煤巖體滲透率比率僅升高至200倍左右。 圖3 保護層底板下煤體滲透率分布[83]Fig.3 Permeability distribution of the coal under the first-mined seam floor[83] 系數擬合型的煤體滲透率模型主要通過試驗數據擬合的手段來確定一系列待定系數的變化與不同區段滲透率的關系。XUE等[84]根據煤體三軸壓縮試驗過程中應力-應變-滲透率關系的變化特征(圖4),將全應力-應變過程劃分為3階段:彈性階段、塑性軟化階段、殘余狀態階段。同時認為彈性階段沒有微裂紋產生,塑性軟化階段萌生大量裂紋,進而結合巷道開挖后圍巖損傷的3區特征,將圍巖的漸進損傷區與全應力-應變過程3階段進行了一一對應:彈性階段對應無損區、塑形軟化階段對應開挖損傷區、殘余狀態階段對應強開挖損傷區。由此,得到了巷道開挖后,掘進工作面周圍煤體的系數擬合型滲透率表達式 (14) 式中,αki,βki,γki(i=1,2,3)分別為不同應力和應變條件下描述滲透率變化的系數;εip為煤進入塑性狀態的應變;εir為煤進入殘余狀態的應變。 圖4 煤的應力-應變-滲透率關系[84]Fig.4 Diagram of stress-strain-permeability for coal samples[84] 圖5為掘進工作面推進過程中周圍煤體內滲透率分布演化結果,周圍煤體的滲透率分布同樣符合三區特征。距離巷道中心較遠處,煤體滲透率處于初始狀態;隨著與巷道中心距離的縮減,無損區內的煤體滲透率由于初始裂隙的閉合而滲透率逐漸減小(圖5 Ⅰ),距離至塑性區的邊界時,滲透率達到最小值;開挖損傷區內由于產生大量裂紋而造成滲透率持續升高(圖5 Ⅱ);強開挖損傷區內煤體破裂程度較為嚴重,由此出現大量貫通裂隙引起滲透率急劇升高(圖5 Ⅲ)。對比不同開挖時間下的滲透率分布結果可知,隨著時間的推移,煤體內滲透率的變化幅度呈上升趨勢。 圖5 掘進工作面周圍煤體滲透率分布[84]Fig.5 Permeability distribution of the coal around the roadway[84] 開采擾動下工作面前方煤體或底板下煤巖體的滲透率均呈現分區段變化的特征,上述3個滲透率模型分別從斷裂力學、細觀損傷力學和連續損傷力學的角度考慮了采動過程中煤體損傷破裂造成的滲透率分區特征。在此之中,有效應力型的模型運用斷裂力學理論,確定了微裂紋的開裂判據,通過損傷理論構建了微裂紋和損傷變量的關系,建立的模型較好的體現了采動應力和損傷破裂特征,模型的理論推導過程較為嚴密,具有較好的基礎理論支撐。幾何參數型的模型加入了煤體參數的微觀統計分布,更加貼近煤體內部孔裂隙結構導致的非均勻性特征,同時模型采用拉伸和剪切破壞準則作為單元失效判據更為全面,模型從細觀損傷本構出發考慮損傷破裂的因素對煤體變形和滲透的影響,適用范圍較廣,但計算中將煤體劃分為細觀單元后,求解計算的工作量較大,所以較為適合進行數值計算。系數擬合型的模型從形式上來看較為簡潔,可顯著區分工作面前方煤體的損傷分布特征,可以較好的反映各損傷區煤體滲透率的變化規律,此外該模型也易于進行理論計算,尤其是便于解析計算。 (1)相比天然氣和煤層氣的開采過程,采動應力環境下的煤層在受力方式和結構形式上更為復雜。工作面推進過程中采動應力的3個應力主方向出現不同的變化趨勢,采動應力可視為外部邊界條件,而煤層由于沉積作用出現的層理和割理結構屬于內部結構條件。煤炭開采過程中,其內部結構和外部邊界條件的主方向并非一致,所以需要考慮外部邊界條件和內部滲透率主方向的夾角問題,統一兩者之間的關系。與此同時,割理結構的各向異性也造成煤體物理力學參數存在異性特征。因此,需要結合地質條件和各向異性的物理力學參數建立一個考慮采動應力、煤層產狀和滲透率方向的模型,以此確定煤層瓦斯滲透的最優化方向,指導煤層增透和瓦斯抽采工作。 (2)采動卸壓是一個打破原始地應力后應力持續重分布引起煤層損傷破裂的增透過程。現有的煤體滲透率模型已經開始逐漸關注到這個問題,然而在已有成果中完全基于損傷理論推導出的損傷滲透率模型還較少,部分經驗模型的實用性較好,但推導過程存在較多前提假設。因此,損傷滲透率模型的理論基礎仍需進一步夯實。除此之外,結合斷裂力學理論對煤體內裂隙演化過程進行定量描述,探究裂隙連通度對煤體滲透性的影響,確定采場尺度下不同裂隙網絡空間分布與煤層滲透性的關系[85-88],建立一個多理論交叉、宏細觀結合的滲透率模型是十分必要的。 (3)煤體吸附應變的研究中,大量的實驗和理論成果都是基于等溫條件獲得,而采面前方煤體內的氣體壓力和溫度由表及內卻是不斷升高的。此外,在瓦斯吸附和解吸過程中,煤體應變嚴格來講并不具有完全可逆的時空演化特征[89-91]。因此,加強非等溫條件下瓦斯吸附特性的研究,掌握瓦斯解吸和吸附過程中煤體應變的差異性對采動影響下煤層滲透率演化過程的精確描述大有裨益。 總體來說,多因素影響下的采動煤體滲透率模型的理論體系并未完全建立,能夠較為系統和完善體現上述特征的采動煤體滲透率模型也還鮮有出現,但煤體滲透率模型在各向異性特征、損傷破裂特征和吸附解吸特征的方面均已取得大量研究成果,以這些成果為基礎的采動煤體滲透率模型將會迅速發展。同時,以上各方面的研究深度及廣度仍需進一步加強。除此之外,采動應力下煤體滲透率模型的研究還有一些問題需要面對。如今,煤炭開采深度的迅速增大給煤體滲透率的研究帶來巨大挑戰。一方面,深部煤體的賦存環境具有“三高”特征,即高溫、高地應力和高巖溶水壓[92-94]。深部開采是多場多相環境共同影響的工程活動,采掘和增透過程中“三高”因素的變化相互耦合,任一因素的變化都將嚴重影響煤層的透氣性效果。因此,深部采動煤體滲透率模型需要解決多場多相耦合的問題。另一方面,深部煤體開采過程中具有顯著的強擾動和強時效特征[95-96]。強擾動是指采掘活動對深部高應力區巖體形成的強烈卸荷效應;強時效是指深部環境下采動巖體具有與采掘活動無關的、明顯的流變效應。顯而易見,強擾動和強時效特征將會強烈影響深部煤體的滲透特性。所以,為了全面反映深部煤體滲透率的控制因素,深部采動煤體滲透率模型還需要考慮強擾動和強時效特征的影響。
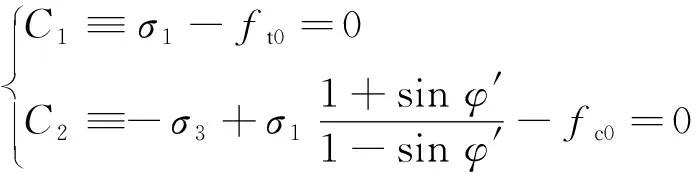
2.3 煤體吸附解吸特征的表征方法
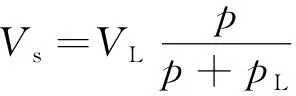

Table4Expressionsofadsorptionstrainbasedonadsorptionthermodynamics
3 采動應力下煤體滲透率模型研究進展
3.1 有效應力型的煤體滲透率模型
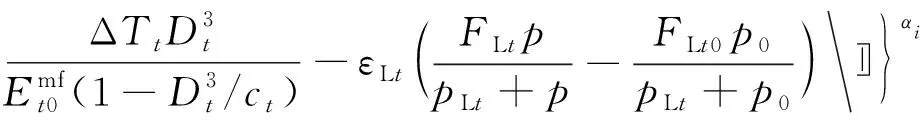
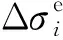
3.2 幾何參數型的煤體滲透率模型
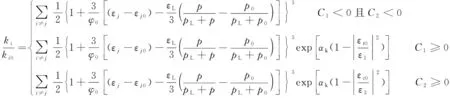
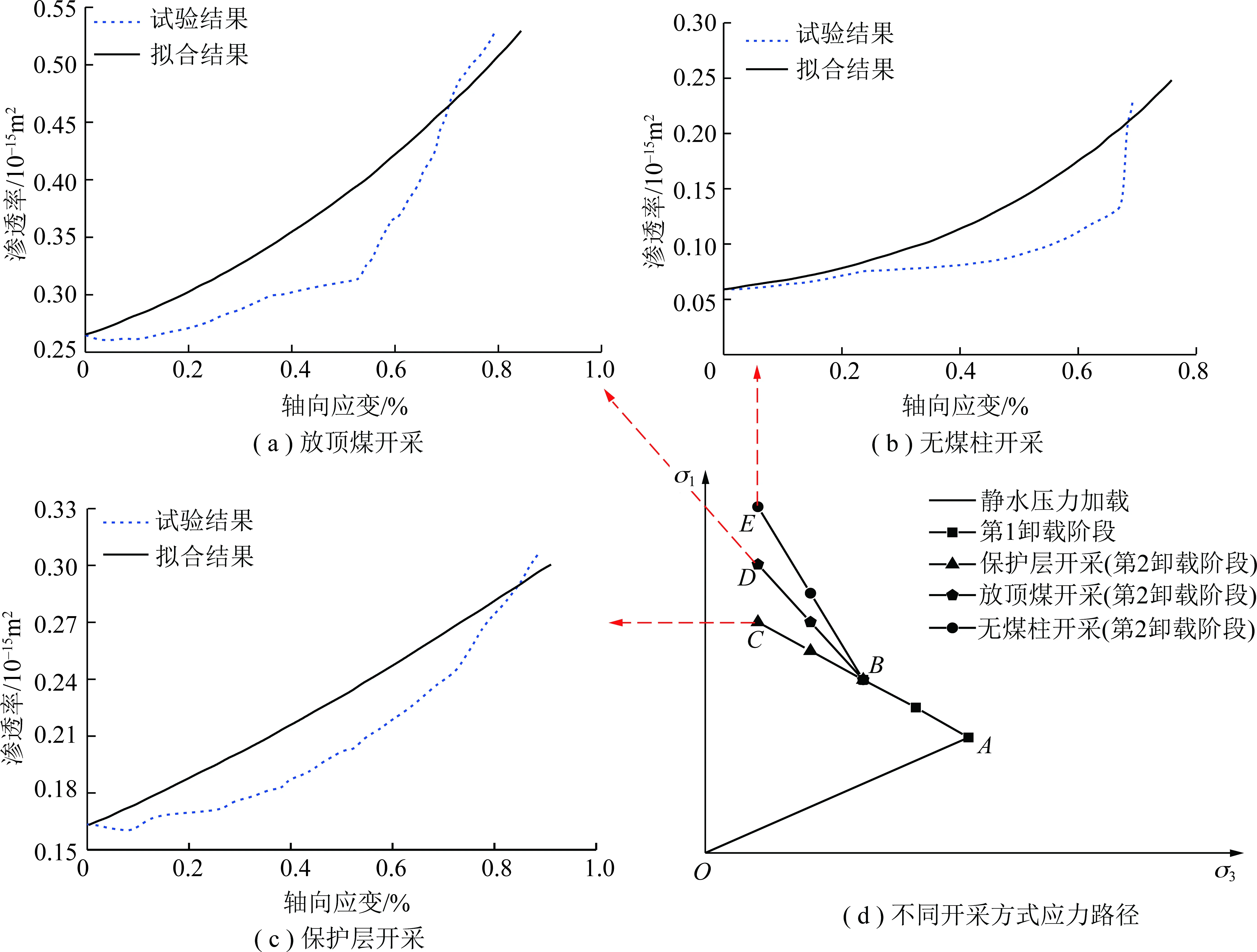
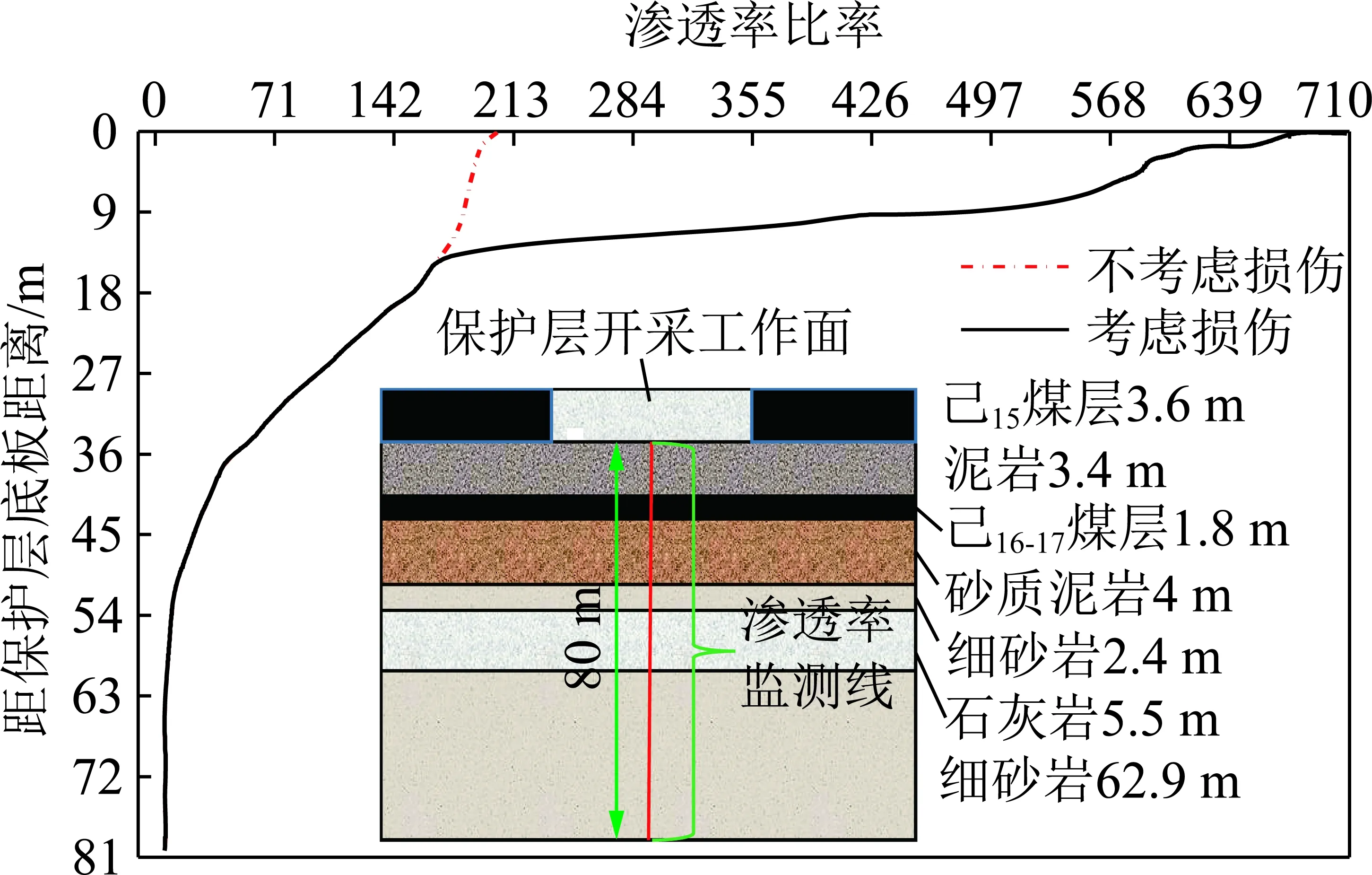
3.3 系數擬合型的煤體滲透率模型

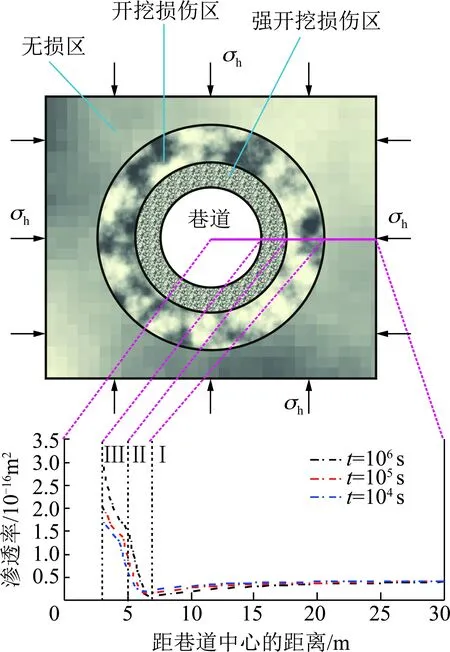
4 結論與展望

