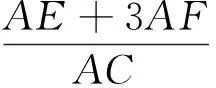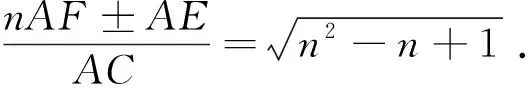核心素養視域下中考試題命制的關注點

浙江省湖州市第五中學 (郵編：313000)

1 關注基本概念，注重數學理解

尊重教材，理解教材，以教材為依據設計試題.一可以充分發揮課本例習題的典型性、代表性和科學性的作用；二可以導引當今數學教學方向，是克服題海戰術和極端功利主義的有效策略.通過教材或配套作業本中典型和具有代表性的例習題的直接引用、改編或引申而成的試題，讓學生既熟悉又陌生，有效地與課本對接，考查對數學概念和數學本質的理解.

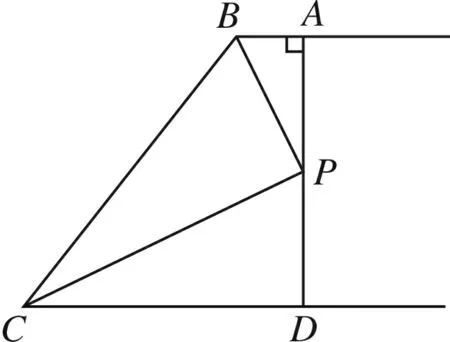
圖1

例1如圖1，AB∥CD,BP和CP分別平分∠ABC和∠DCB,AD過點P,且與AB垂直.若AD=8，則點P到BC的距離是( )

A．8 B．6 C．4 D．2

評注本題深入發掘課本中角平分線的性質定理，通過隱含條件“點P到BC的垂線段”這橋梁，添輔助線得到AP=PD,從而解決問題.很好地考查了學生對角平分線相關知識的理解、掌握和靈活運用的程度.

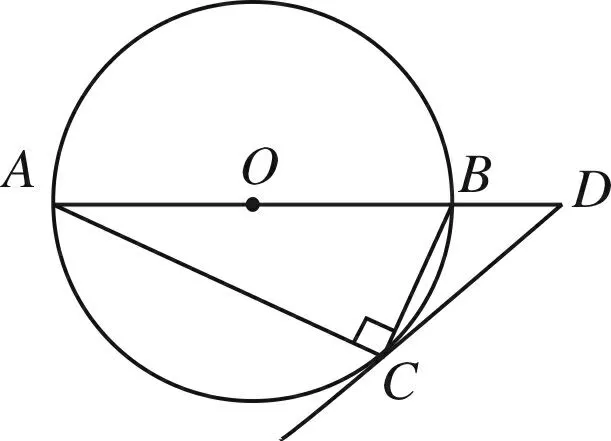
圖2

例2如圖2，圓O是Rt△ABC的外接圓，∠ACB=90°，∠A=25°. 過點C作圓O的切線，交AB的延長線于點D，則∠D的度數是( )

A．25° B．40° C．50° D．65°

評注本題深入發掘課本中切線的定義，90°的圓周角所對的弦是直徑來解決問題，背景來源于課本，突出課堂教學引導學生經歷概念形成過程和理解概念本質的重要性，對教學有很好的指導作用.

2 貼近生活實際，突出時代氣息

以社會熱點、旅游、農業、校園拓展類課程、社會養老問題為背景設計數學問題，考查知識點分別為圖形的對稱、科學計數法、反比例函數、統計、方程和函數建模思想等數學知識和方法解決實際生活問題.既充滿時代氣息，關注社會經濟發展，又較好地反映了數學來源于生活又服務于生活的宗旨.

例3為了迎接杭州G20峰會，某校開展了設計“YJG20”圖標的活動．下列圖形中既是軸對稱圖形又是中心對稱圖形的是

評注本題以在杭州召開的杭州G20峰會為背景，考查了圖形對稱這一知識點，突出了時代氣息，讓學生在學習知識的同時也能關注時政熱點.

例4隨著某市養老機構(養老機構指社會福利院、養老院、社區養老中心等)建設穩步推進，擁有的養老床位數不斷增加.

(1)該市的養老床位數從2013年底的2萬個增長到2015年底的2.88萬個.求該市這兩年(從2013年底到2015年底)擁有的養老床位數的平均年增長率；

(2)若該市某社區今年準備新建一養老中心，其中規劃建造三類養老專用房間共100間，這三類養老專用房間分別為單人間(1個養老床位)，雙人間(2個養老床位)，三間(3個養老床位).因實際需要,單人間房間數在10至30之間(包括10和30)， 且雙人間的房間數是單人間的2倍.設規劃建造單人間的房間數為t.

①若該養老中心建成后可提供養老床位200個，求t的值；

②求該養老中心建成后最多提供養老床位多少個？最少提供養老床位多少個？

評注本題隨著社會老齡化日趨嚴重，養老問題已成社會重大民生問題之一.以湖州市養老機構的實際情況為背景，以及近幾年湖州市每千名老人擁有的養老床位每年增長的情況命制.數據具有真實性和可靠性，考查了學生的閱讀素養.通過對一元一次方程、一元二次方程、一次函數增減性等知識點和建模等思想方法解決實際問題的考查，意在檢測學生閱讀分析能力和解決問題的能力.

3 滲透PISA理念，關注數學本質

學以致用是學生學習的驅動力，只有學生真切感受到知識的應用價值，才能主動有效地學習.本題的取材內容貼近學生生活實際，使學生深刻感受到課堂上所學知識的實用性，體會到所學知識具有巨大的實際意義.

圖3

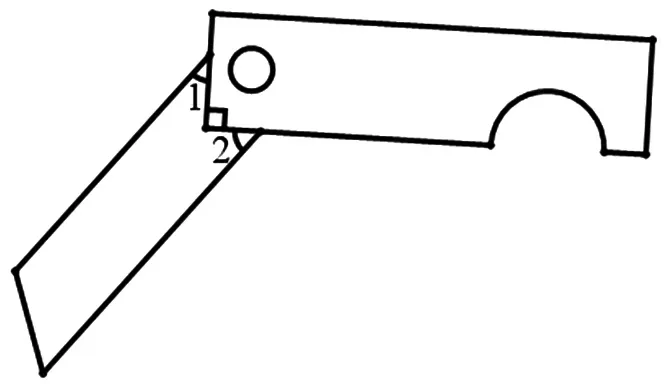
圖4

例5圖3是我們常用的折疊式小刀．圖4中刀柄外形是一個矩形挖去一個小半圓，其中刀片的兩條邊緣線可看成兩條平行的線段，轉動刀片時會形成圖4所示的∠1與∠2，則∠1與∠2的度數和是度.

評注試題蘊含著PISA理念：

一是含有“情境”，讓每個學生都能參與到數學化過程中；二是關注運用，以學生熟悉的小刀片為背景，提煉出圖形編制而成.

題中的“動中有靜”,生活氣息濃厚，但對知識點的考查又很簡單.刀片轉動中，∠1與∠2的度數和是一個定值.表面上此題僅僅考查了平行線的性質；實際上重點考查了數學的應用意識和解決問題的能力.并鼓勵學生關注和熱愛生活，善于利用數學思維來解決問題.

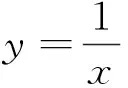
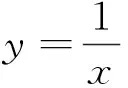
A．命題(1)與命題(2)都是真命題

B．命題(1)與命題(2)都是假命題

C．命題(1)是假命題，命題(2)是真命題

D．命題(1)是真命題，命題(2)是假命題

點評大家知道，數學的6個核心素養是：數學抽象、邏輯推理、數學建模、運算能力、直觀想象、數據分析.本題通過閱讀提煉和抽象出“派生函數”的定性性質：圖象的對稱軸在y軸的左側和“派生函數”的定量性質：圖象都經過同一點(0,0)是解決本問題的關鍵.試題難度不大，但卻是考查學生核心素養的一種較好的嘗試.

例7已知四個有理數a、b、x、y同時滿足以下關系式：b>a，x+y=a+b，y-x

點評初看題目，認為四個有理數的大小比較應該不會困難，通過嘗試發現試題內涵豐富，解法眾多，是一道值得研究的好題.

4 探究動態問題，感受數學之美

動點問題年年有，我們翻看大多數的動點問題，一般都是點動牽引線動或點、線的動帶動局部形狀發生變化，下面的三類原創動點問題是通過折疊、平移、旋轉的方法呈現的.目的是讓考生通過“動中有靜”的探究，關注數學學習的思想方法,凸顯數學學習本質，試題的“動”較有特色.

圖5

圖6

圖7

例8如圖5，在等腰三角形ABC中，AB=AC=4，BC=7.如圖6，在底邊BC上取一點D，連結AD，使得∠DAC=∠ACD.如圖7，將△ACD沿著AD所在直線折疊，使得點C落在點E處，連結BE，得到四邊形ABED.則BE的長是

評注試題緊緊圍繞著“四基”：基礎知識，基本技能，基本思想方法，基本活動經驗.主要考查了等腰三角形的性質，折疊的本質，平行四邊形的性質，直角三角形勾股定理.如果注意觀察，挖掘出隱含著圓，則容易證得AC∥BE，這對問題的求解是事半功倍的.

這類試題屢見不鮮，它既可以考查學生動手探索數學問題的能力，又能考查數學思維能力.該問題通過折疊這一熟悉的問題背景，將特殊三角形，平行四邊形等相關知識有機地串聯，讓學生經歷操作——觀察——探究——計算的活動過程，在準確理解操作過程，分析操作結果獲得數學知識.本問題是選取了這類折疊問題中的一個特殊位置來考查學生對折疊過程中圖形本質的理解.在指導學生學習這類問題的解決策略的同時，還可以借助此類問題的背景，進行變式探究.例如：

變式一在等腰三角形ABC中，AB=AC=4，BC=7.在底邊BC上取一點D，連結AD.將△ACD沿著AD所在直線折疊，使得點C落在點E處，使得△ACF為直角三角形.求CD的長.

圖8

圖9

變式二在等腰三角形ABC中，AB=AC=4，BC=7.在底邊BC上取一點D，連結AD.將△ACD沿著AD所在直線折疊，使得點C落在點E處，使得△CDE為直角三角形.求CD的長.

圖10

圖11

變式三在等腰三角形ABC中，AB=AC=4，BC=7.在底邊BC上取一點D，連結AD.將△ACD沿著AD所在直線折疊，使得點C落在點E處，使得△ACD是等腰三角形.求BE的長.

圖12

圖13

以上問題構成了一個問題串，通過這樣一個問題串的研究，可以進一步探究發現，上述翻折問題的本質是一個點在圓上的運動的特殊位置.即以點E在點A為圓心，AC為圓心的圓上運動，以及∠CAE的角平分線AD之間所構成的位置和數量關系.

該題需要用動態的眼光分析，解決問題的靈活思維能力體現了新課程所倡導的動手實踐自主探索的學習方式，同時該題在初中階段學習的基礎上，有意識地給學生今后的數學學習做了一個較好的準備和鋪墊，有效地與立體幾何在數學思維上進行了銜接，起到了橋梁延伸的作用.無獨有偶，2016年浙江高考理科卷中第14題，實質上也是對這類折疊問題在空間上的探究，在初中階段的平面范圍內與高中數學空間范圍內，兩題呈現出“姐妹題”，是一次奇妙的高考題與中考題的偶遇，產生了遙相呼應的同頻效果.

圖14

變式四(2016年浙江理科高考題)在△ABC中，AB=BC=2,∠ABC=120°.若平面ABC外的點P和線段AC上的點D,滿足PD=DA,PB=BA,則四面體PBCD的體積的最大值是.

圖15

例9已知點P在一次函數y=kx+b(k,b為常數，且k<0，b>0)的圖象上，將點P向左平移1個單位，再向上平移2個單位得到點Q，點Q也在該函數y=kx+b的圖象上.

(1)k的值是；

評注本題的動中有靜是直線無論上下或左右平移，其中的待定系數k是不變的.本問題的設置較好地詮釋了k的幾何意義.通過設點P為(0,b)，根據點P的平移，得到平移后的點為(-1，b+2)仍在直線y=kx+b上，可得：b+2=-k+b，從而求出k=-2.在這里很好地為考生的后續學習打下伏筆.

圖16

圖17

圖18

例10數學活動課上，某學習小組對有一內角為120°的平行四邊形ABCD(∠BAD=120°)進行探究： 將一塊含60°的直角三角板如圖放置在平行四邊形ABCD所在平面內旋轉，且60°角的頂點始終與點C重合，較短的直角邊和斜邊所在的兩直線分別交線段AB，AD于點E，F(不包括線段的端點).

(1)初步嘗試

如圖16，若AD=AB，求證：①△BCE≌△ACF，②AE+AF=AC；

(2)類比發現

如圖17，若AD=2AB，過點C作CH⊥AD于點H，求證：AE=2FH；

(3)深入探究

總而言之，由于試題兼顧畢業與升學兩重功能，因此數學的核心內容和主要思想方法是考查的重點，基礎性和常規性是試題的主體.大部分試題來源于課本例習題和浙江省教研室編寫的作業本改編而成的.試題從學科知識特點、學科思想方法和初高中銜接三個維度出發，加強對數學概念、數學本質、學習潛能和思想方法的考查.同時，重視滲透數學史、數學文化、PISA教育理念等.試題呈現形式多姿多彩，既要富有時代氣息的正能量，又要蘊含豐富數學內涵創新思想.因此試卷的基礎性、思想性、時代性、人文性、應用性、探究性、銜接性必須兼顧，試題設計必須：梯度明顯、難度適中，目的使不同層次的考生發揮出自己的真實的水平.因此,中考復習要重視回歸課本，關注思想方法，強化應用意識，突出發展能力.