高三課堂教學聚焦高考 助力學科素養
江蘇省吳縣中學 (郵編:215151)
縱觀近些年高考題,試題不再是追求知識的全面覆蓋,而是更加凸顯了考察學生的能力,將素養作為立足點,注重了數學本質和通性通法的考察.一定程度上還淡化了解題技巧,將考察的重心轉移到了數學核心素養上.試題中還更多的融入了數學文化,符合了新課標的要求,彰顯了素質教育,關注了學生綜合能力的培養.
1 高考的趨勢
隨著《普通高中數學課程標準(2017年版)》頒布,現在的高考正在從原來的單純解題能力的考察向學科素養進行轉變,各地高考卷均體現了:注重基礎、平穩過渡,試題更加傾向于數學應用、數學核心素養的考察.
高三課堂教學也應該遵循高考命題趨勢的變化,注重數學的基本概念、法則、公式、定理、經典問題的教學.讓學生內化于理解,外化于應用,重視解題通性通法,由“技巧”教學向素養能力培養過度.同時教學過程中也需要加強對學生數學思想的灌輸,讓高三教學從單純的“解題”向“理解應用”過渡轉變.真正符合2017年版的新課標中的:提高從數學角度發現問題和提出問題的能力、分析問題和解決問題的能力.
新的高中數學課程標準中明確提出了“四基四能+六個核心素養+數學情感態度與數學精神”的課程目標.所以高考數學卷中增加了考察素養、能力題的比重,同時還不斷增加了數學文化的滲透.傳統教學模式、題海戰術也失去了原有的效果,高三的課堂教學應該更多的聚焦在學生能力培養上,只有這樣才能真正的助力學生數學學科素養.
2 高效課堂助力學科素養
高三復習課注重高效,既要讓學生重視基礎知識的“回爐”,也要重視經典例題的反復,更要提升對問題本質的把控.那么教師怎樣才能做到這樣高效的課堂教學呢?筆者認為要從以下幾點來實現:
2.1 課堂起點低,注重基礎問題
高三復習課應該以知識點作為入口,引導學生重視數學概念、基礎知識,更要讓學生腦海中串聯各個知識板塊之間的聯系,重視數學問題本質的理解.切記不能急于展示難度較大的題型,企圖以這樣的高難度問題來提升培養學生的思維能力.殊不知這樣除了增加學生對數學的畏難情緒,還會讓其產生依賴性,導致以后遇到難題,就等著老師評講點撥,久而久之數學解題能力非但沒有提高,反而帶來了負面的影響.
高考題往往都是源于課本,那些讓學生感到生疏的問題,常常是教材上基礎問題通過變形、加工而來的,所以關注基礎,回歸教材是高三課堂的根本.數學的基礎知識如同是給學生建造房子的根基,根基越扎實,學生堆砌的房子才能越高,才可以為后期數學難度的提升做好伏筆.反之如若基礎沒有打扎實,那么后期想要拔高難度則會變得愈發困難,向前推進速度反而會受到制約.
2.2 重視解題規范,減少無謂失分
現在的高考卷多以常規題出現,試題類型基本固定.但是往往看似簡單的題目,學生想要拿滿分或者高分卻也不容易.從高考閱卷者反饋的信息來看,答題不規范、書寫不嚴謹、非能力性的失分還是比較普遍的.這就要求高三教學中要規范學生的書寫,嚴格要求,當然在要求學生的同時,教師首先要做到板書工整、條理清晰,給學生起到良好的示范作用.
在平時練習中教師不僅提醒學生重視書寫字跡清楚、過程條理連貫,減少因卷面不整潔或草稿凌亂而導致的失分,同時還要培養學生規范答題、優化答題的意識,解題要踩得住得分點.同時在批閱學生的練習時,特別是解答題時候,過程中也不能僅僅關注最終答案,更要關注學生答題是否規范、嚴謹,必須做到:步步有依據,條條都嚴謹.
2.3難度螺旋式上升,步伐跨度要小
高三復習課堂中教師經常采用例題評講式教學,評講過程中教師應該注意例題的難度,要符合學生思維的層次.因為在課堂上,學生的思維是螺旋式上升的,如果教師所設計的例題難度較大,那么學生的思維可能會受到阻礙.所以根據不同層次的學生,所設計的問題也應該具有貼切性.如果例題有難度,教師則可以適當的鋪設“臺階”,讓學生逐步探索逼近所要研究的問題,通過層層遞進的方式,啟發學生的思維.
案例1(2017年杭州市第二次高考科目教學質量檢測高三數學檢測試卷第9題)記M的最大值和最小值分別為Mmax、Mmin,若平面向量a、b、c滿足,|a|=|b|=a·b=c·(a+2b-2c)則( )
此題上手難度較大,學生會對已知條件中的連等式產生“畏懼情緒”,教師在評講此題時,可設計多個小題,將難度降低,給學生做好鋪墊,當然問題之間也應該做到過度需自然:
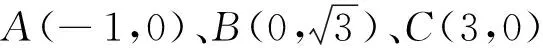
(2)已知a、b為單位向量,a·b=0,若向量c滿足|c-a-b|=1,則|c|最大值為.
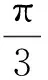
2.4 落腳點要高,提升解題能力
當然,高三的復習課,最終的目標還是要指向高考的,所以課堂的最終落腳點一定要有“高度和深度”.當然落腳點雖高,但是也要讓學生知道,無論多么高深的高考題,它的來源始終是教材(源于教材又高于教材).
案例2定義在R上的奇函數,在[0,+∞)為增函數,則不等式f(3x-2) 變式(1) 減函數y=f(x)定義在[1,1]上,且為奇函數,f(3x-2) 變式(2) 設f(x)是定義在R上的增函數,對任意x,都有f(-x)+f(x)=0恒成立,若實數m、x滿足不等式f(m2-6m+21)+f(n2-8n)<0,則m2+n2的取值范圍. 變式(4) 已知函數f(x)是定義在R上的奇函數,且x>0時,f(x)=x2則任意x∈[t,t+2],f(x)≥9f(x+t),則t的最大值為. 高三課堂教學教師往往采用的變式教學,變式教學的起點可以低點,但是最終的變式一定要達到高考的要求(當然也應該根據學生實際的情況來選擇例題的難易程度).上述變式題由易到難,遵循學生思維遞進過程,同時不僅僅局限在基礎回顧,通過層層遞進,最終還完成了高落點的課堂效果.低起點有利于學生鞏固基礎,高落點則可以提升學生數學思維發散、創新能力. 數學思想是學生提升數學核心素養的助推器,新課標所提及的數學學科的六大核心素養,是在原有的知識技能、過程方法、情感態度價值觀上提煉而成的.對學生在數學理解,思想方法的掌握上提出了更高的要求.所以在高三數學復習過程中,教師要從整體把握,既要關注單獨的知識點,更要打破原有的固定模塊限制,幫助學生疏通所有知識的脈絡,通過聯系類比,將數學的思想滲透在課堂的每個“環節”.讓學生參與到數學思想形成的過程中來,思想的形成不是“被告知”的,是在參與過程中體驗、感悟、提煉出來的. 隨著新課標(2017版)的實施和各地高考改革的不斷深入,新高考一定會加大考察數學核心素養的力度,當然素養的考察一定是以數學知識作為基礎,通過數學能力展示出來的.這也避免了對知識的死記硬背,避免試圖通過大量的題海戰術來提升成績的不良導向.同時對教師也提出了更高的要求:向課堂要效率、助學生提能力.筆者對高三教學還有如下幾點思考,不當之處還請各位專家批評指正: 多地高考卷已經取消了文理分科,或即將進入文理同卷的高考模式.例如:天津市將在2019年進入新高考模式,文理同卷.這就要求教師在教學過程中定位文理生差異時,不能像以往一樣:降低對文科生的要求.現在因充分考慮到文理科考生未來發展不同需求的同時,也要增強對文科學好數學的要求.高三課堂需要分層教學,需要把控難度,但是更重要的是在提升學科知識能力、培養核心素養上下功夫,最終為學生的終身發展奠定良好的基礎. 王梓坤教授就曾經說過:“數學文化具有比數學知識體系更為豐富和深邃的文化內涵,數學文化是對數學知識、技能、能力和素質等概念的高度概括.”我們學習數學不僅是為了獲取知識,更需要通過數學學習接受數學精神、數學思想和數學方法的熏陶,提高思維能力,鍛煉良好的意志品質. 學好數學需要經歷四步:第一步是弄“會”,會運用數學概念、公式、定理解題,了解概念公式定理的外延,變式等;第二步是弄“通”,“會了”不一定“通了”,它們的境界是不同的,有些學生會做題了,但只是局限在套用公式,靈活性欠缺.“通”就是要對數學問題融會貫通,包括對公式正用、逆用、變形用、靈活用等等;第三步是勤“思”,數學學習需要勤思考,數學解題更需要思考:思考數學的本質、思考解題的思路,尋求解題最優解、思考過程中涉及的數學思想,經歷了思考,學生能力才能真正提升;第四步是感“悟”,數學思想、數學文化、核心素養不是教師“教”出來的,是學生撥開云霧自己“悟”出來的,通過感悟各個模塊的知識間的聯系,找到解題的通性通法,做到“生題尋舊題,聯想生思路,感悟提思維,提煉育素養”. 高三看似時間寬裕,但是由于內容涵蓋了高中所有內容,而且教學進度會受到統一考試的影響,所以實則高三復習的任務十分的繁重.教師課堂上表面習題沒有少講,實則沒有將問題講透徹,往往是“淺嘗即止”,這樣的復習效果可想而知.筆者認為高三課堂無需注重量,而應該重視質,在講透一類型題目的同時,還要在此基礎上進一步拓展,將“問題連根拔起”.這樣一定程度也會減輕學生解題負擔,達到“弱水三千,只取一瓢”效果,提升高三復習課堂的效率. 所以這就需要教師在課前下苦功夫,既要認真選擇高質量的習題,又要將這些習題進行比較刪選,要從不同角度、不同高度深度研究它們,找出共性和差異.這樣才能更有收獲,才可以幫助學生在高三復習過程中找到“高效之路”. 高三前期的教學務必要“慢”,在“慢”中鞏固學生的基礎,傾聽學生的思路,讓學生充分的表達,充分的吸收、消化,這樣才能為中后期能力提升打下堅實的基礎. 高三中后期的教學則需要“高”、“快”,觀察問題的視角要高,課堂的落腳點定位要高,高落點、高視角有助于學生迅速在原有基礎上提升能力,拔高思維.課堂節奏則要“快”,如果還是慢節奏,會讓學生思維發展受到制約.“快”節奏不僅可以訓練學生的解題速度,也可以加快學生腦海中搜尋記憶的速度,正所謂:“熟能生巧,快而精準”. 總之,高考對高三的教學具有著明確的導向性,教師研究高考要立足于數學的核心素養,關注發展方向,聯系學生的實際狀況,優化改進課堂教學,幫助學生突破自我,爭取在高考中收獲滿意的答卷,最終完成立德樹人這一教育的根本目標,同時也助力發展學生的核心素養.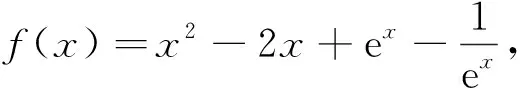
2.5 滲透數學思想,助力學科素養
3 教學思考
3.1 淡化文理科學生的差異
3.2 重視數學思想、數學文化培養,突出創新能力的發展
3.3 重視習題深度探索,減輕學生題海勞動量
4 結束語

