教學(xué)設(shè)計(jì)應(yīng)追求教材知識結(jié)構(gòu)與學(xué)生認(rèn)知水平的和諧統(tǒng)一

安徽省合肥市教育科學(xué)研究院 (郵編：230071)

筆者是合肥市中學(xué)數(shù)學(xué)教研員，從自己大量的聽課和各種推送賽課的過程中，深感影響課堂教學(xué)成敗的因素很多，但最主要和最直接的因素是“教學(xué)設(shè)計(jì)”的合理性.2018年10月份安徽省數(shù)學(xué)會在合肥市舉辦了全省高中數(shù)學(xué)骨干教師課堂教學(xué)展示活動，本人有幸參與了點(diǎn)評.在欣賞安徽省骨干教師高素質(zhì)的同時(shí)，就其中一節(jié)課教學(xué)內(nèi)容，談?wù)勗鯓釉O(shè)計(jì)更合理？因?yàn)榻滩氖钦n程標(biāo)準(zhǔn)的具體體現(xiàn)，又是教師教學(xué)設(shè)計(jì)的依據(jù)，所以本文就人教A版教材必修2中第二章第三節(jié)第一小節(jié)《直線與平面垂直的判定》(第一課時(shí))的教學(xué)內(nèi)容，談?wù)勅绾伪M可能達(dá)到教材知識結(jié)構(gòu)和學(xué)生認(rèn)知水平的和諧統(tǒng)一.

1 教材呈現(xiàn)

1.1 課時(shí)內(nèi)容

教材從給出現(xiàn)實(shí)生活中的旗桿與地面，大橋的橋柱與水面的位置關(guān)系出發(fā)，觀察在陽光下旗桿與它在地面上的影子，感悟旗桿AB所在的直線與地面內(nèi)任意一條直線垂直；從而得出直線與平面垂直的定義；再通過折紙?zhí)骄浚贸鲋本€與平面垂直的判定定理；最后，講解一條直線與平面垂直的判定定理的例題.

1.2 前后聯(lián)系

在學(xué)習(xí)此節(jié)課以前，教材安排了：2.1 空間點(diǎn)、直線、平面之間的位置關(guān)系；直線與平面平行的判定及其性質(zhì).此節(jié)課以后，教材安排了：2.3.2 平面與平面垂直的判定；2.3.3 直線與平面垂直的性質(zhì)；2.3.4 平面與平面垂直的性質(zhì).

與此節(jié)課有密切聯(lián)系的內(nèi)容，前面已學(xué)：直線與平面的位置關(guān)系；后續(xù)學(xué)習(xí)：直線與平面所成的角；平面與平面垂直的判定.

2 學(xué)生認(rèn)知

按照安徽省大部分地市進(jìn)行教學(xué)的順序是高一學(xué)習(xí)必修1、4、5、3，高二學(xué)習(xí)必修2 及選修內(nèi)容.因此，此節(jié)課是高二學(xué)生學(xué)習(xí)的內(nèi)容，學(xué)生對知識的理解力和統(tǒng)攝力有了較大的提高.與此節(jié)課有緊密聯(lián)系的是：在知識層面上，學(xué)生已經(jīng)具備，初中學(xué)習(xí)了：在同一平面內(nèi)兩直線垂直的判定；高中學(xué)習(xí)了：空間中直線與平面的位置關(guān)系；空間中兩直線垂直的判定.在認(rèn)知上，具備了直線與平面平行的判定的研究基礎(chǔ).

3 設(shè)計(jì)思考

教材的知識結(jié)構(gòu)，讓學(xué)生“觀察在陽光下旗桿與它在地面上的影子，感悟旗桿所在的直線與地面內(nèi)任意一條直線垂直”，從而得出直線與平面垂直的定義.其實(shí)，由上面學(xué)生認(rèn)知可知，直線與平面的位置關(guān)系是用直線與平面的公共點(diǎn)來定義的，且與此節(jié)課緊密聯(lián)系的“直線與平面平行的定義”的得出是直接給出的，學(xué)生也極易接受.而學(xué)生學(xué)習(xí)直線與平面垂直的定義前，學(xué)生對垂直的概念學(xué)生習(xí)得的只有：直線與直線垂直，對直線與平面垂直只是“感覺”，沒有對直線與平面整體垂直的認(rèn)知基礎(chǔ)，教材也只是為了定義“強(qiáng)加”給學(xué)生的“旗桿所在的直線與地面內(nèi)任意一條直線垂直”.因此，這一節(jié)課教材的知識結(jié)構(gòu)與學(xué)生的認(rèn)知水平及認(rèn)知結(jié)構(gòu)不一致，教學(xué)中一定存在教學(xué)不自然或教師“強(qiáng)推”的現(xiàn)象.

對“直線與平面垂直”的判定定理的得出過程，類比“直線與平面平行”的得出是困難的.因?yàn)椤爸本€與平面沒有公共點(diǎn)”是“直線與平面平行”的定義，把“直線與平面沒有公共點(diǎn)”轉(zhuǎn)化為“平面外直線與平面內(nèi)的直線無公共點(diǎn)”是尋找“線面平行”的充分條件.由于平面外直線與平面內(nèi)直線的位置關(guān)系有：平行或異面.兩直線異面難以判定，而兩直線平行易于判定，因?yàn)閮芍本€平行，則此兩直線是共面的，所以學(xué)生判定的方法很多.因而，把“直線與平面沒有公共點(diǎn)”的問題轉(zhuǎn)化為“過面內(nèi)所有點(diǎn)都有直線與已知直線平行”的問題，再將面內(nèi)過所有點(diǎn)的平行直線減少至一條，由于線面平行同時(shí)把線面相交的情況加以否定，這樣就得到直線與平面平行的判定.而“直線與平面垂直”的定義是“直線與平面內(nèi)任意一條直線垂直”，即直線外一條直線與平面內(nèi)所有直線垂直.顯然，總體思維上難以類比，但怎么讓面內(nèi)無數(shù)且無序的直線條數(shù)減少的思維是一致的.而面內(nèi)直線減少至直線有“兩條”且“相交”，在減少面內(nèi)直線的過程中，比前者少了“去異面直線”的過程，好在直線與面內(nèi)“一條”直線垂直是不能判斷線面垂直，只要通過學(xué)生“直觀操作”就可以明確，因而兩直線“相交”是得出判定定理之難點(diǎn).

4 具體設(shè)計(jì)

4.1 引入

(1)空間中直線與平面的位置關(guān)系有哪些？

(2)“直線在平面外”中，“直線與平面平行”是怎樣由定義得出判定的？

(3)我們已經(jīng)學(xué)習(xí)了線面平行的定義，判定和性質(zhì)，而“直線在平面外”中，還有一類位置關(guān)系是什么？請同學(xué)們在現(xiàn)實(shí)生活中舉出與這一位置關(guān)系類似的情景？

設(shè)計(jì)意圖問題(1)：從與此節(jié)內(nèi)容緊密聯(lián)系的“直線與平面的位置關(guān)系”出發(fā)，從總體上把握位置關(guān)系的知識結(jié)構(gòu)；問題(2)：直線在平面外的位置關(guān)系中，已經(jīng)研究了直線與平面平行位置關(guān)系的判定和性質(zhì)，與此節(jié)課緊密聯(lián)系的是：直線與平面平行判定的探究和思考過程，以期學(xué)生類比得出研究直線與平面垂直的思路.問題(3)：已經(jīng)學(xué)習(xí)了直線和平面有二(或三)種位置關(guān)系，已經(jīng)掌握了直線和平面平行的定義，判定和性質(zhì)，還有一種位置關(guān)系：直線與平面相交.讓學(xué)生在認(rèn)知結(jié)構(gòu)上產(chǎn)生認(rèn)知的需求，這時(shí)引導(dǎo)學(xué)生回到現(xiàn)實(shí)生活中，直觀感悟直線與平面相交的現(xiàn)實(shí)情境，估計(jì)大部分學(xué)生都會舉出“直線與平面垂直”的生活情境，少數(shù)學(xué)生舉出“直線與平面斜交”的情境，因?yàn)樯钪星罢叱Ｒ?直線與平面斜交的情況，過于一般，研究價(jià)值不大.因而重點(diǎn)研究“直線與平面垂直”的特殊情況.學(xué)生很容易想到：天安門廣場和操場上立一面五星紅旗，將旗桿抽象成一條直線，地面抽象成一個(gè)平面，“怎樣檢驗(yàn)旗桿與地面是不是垂直”.這個(gè)問題就是“如何判定直線與平面是否垂直”的問題，也就是今天我們要研究的課題.

4.2 新知

4.2.1 線面垂直的定義

(1)天安門廣場和操場上立的一面五星紅旗，將旗桿抽象成一條直線，地面抽象成一個(gè)平面，大家想象一下，這種直線與平面的位置關(guān)系你認(rèn)為取一個(gè)什么名字合適？

(2)既然大家都認(rèn)為“垂直”合適，那么大家能不能講講道理呢？

(3)同學(xué)們回答的都有道理，那么面內(nèi)有很多直線，都與已知直線垂直嗎？怎么理解？

設(shè)計(jì)意圖問題(1)由于學(xué)生對空間中線線的位置關(guān)系比較熟悉，而線與線相交的平面問題更清楚，學(xué)生類比平面中線線的位置關(guān)系，通過類比不難得出這種特殊位置關(guān)系是直線與平面“垂直”；問題(2)讓學(xué)生展開想象的翅膀，感知定義名稱與內(nèi)涵的合理性.學(xué)生可能有以下想法：如果把平面看成一條線，就是兩條直線互相垂直，否則“旗桿”就是“歪”的；由于學(xué)生在學(xué)習(xí)線面平行的判定過程中，尋找面內(nèi)直線與已知直線平行的啟發(fā)，線面垂直的定義，是面內(nèi)直線與已知直線垂直所致.問題(3)不能讓學(xué)生操作發(fā)現(xiàn)或演示“旗桿與旗桿影的垂直”，得出定義.其一，后面判定的得出有：操作確認(rèn)的過程；其二，邏輯上有“循環(huán)論證”之嫌；其三，學(xué)生認(rèn)知的基礎(chǔ)只有兩直線的共面垂直和異面垂直的基礎(chǔ).因此，把線面垂直的問題轉(zhuǎn)化為線線垂直的問題，符合學(xué)生認(rèn)知的水平.建議用下面方法，在黑板上畫出或ppt演示下面圖形：

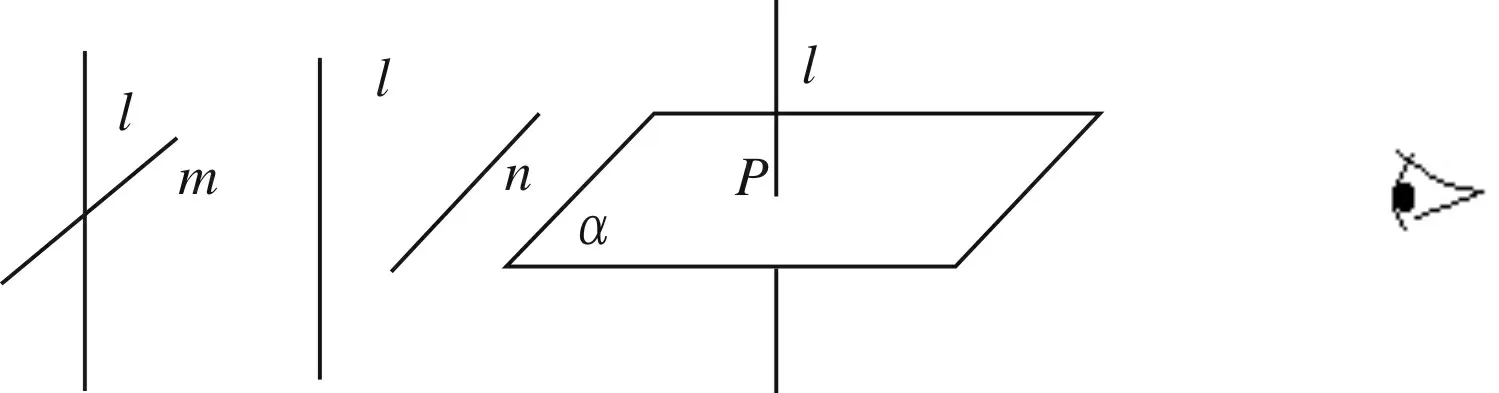
圖1圖2圖3眼

圖1是兩直線共面垂直，圖2兩直線異面垂直，“旗桿與地面”的位置關(guān)系如圖3所示，假設(shè)直線m//n,m、n和表示眼睛的點(diǎn)在平面α內(nèi)，只不過圖形表示的時(shí)候是分開表示的.若你站在足夠遠(yuǎn)的地方從右向左分別看圖1、圖2，并在表示平面α的平行四邊形的外，看圖3，你看到的圖形是什么？(都是兩條互相垂直的共面直線).再將直線m、n平移至平面α內(nèi)，且點(diǎn)P∈m∩l,P?n，這時(shí)圖3中平面α內(nèi)的直線m、n與直線l有什么樣的位置關(guān)系？如下圖4所示：

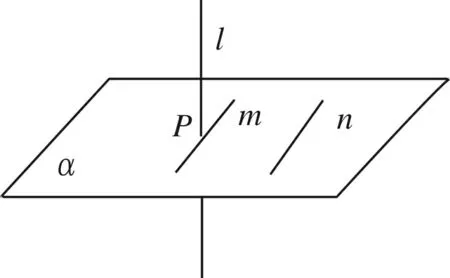
圖4

你能夠進(jìn)一步得出什么結(jié)論？(平面內(nèi)所有與直線m平行的直線都與直線l垂直，即與直線m平行的直線“鋪滿”平面α，都與直線l垂直).平面內(nèi)還有其他方向的直線與直線l有什么位置關(guān)系，怎么“看”呢？(移動“眼”到恰當(dāng)?shù)奈恢茫希梢浴翱础逼渌较虻闹本€與直線l也垂直)你又得出什么結(jié)論呢？(平面α內(nèi)任意一條直線都與直線l垂直).從而得出直線與平面垂直的定義.

定義如果直線l與平面α內(nèi)的任意一條直線都垂直，我們就說直線l與平面α互相垂直，記作：l⊥α.直線l叫做平面α的垂線，平面α叫做直線l的垂面.直線與平面垂直時(shí)，它們唯一的公共點(diǎn)P叫做垂足.

4.2.2 線面垂直的判定

(1)根據(jù)定義判定直線與平面垂直，需要判定直線與平面內(nèi)“任何一條直線”即“所有直線”都垂直，這種判定方法甚至是無法實(shí)現(xiàn)的，那么，我們能否類比線面平行的判定定理得出的過程，思考一下由“線面垂直定義”到“線面垂直判定”的研究思路或方法？

(2)大家一致認(rèn)為把面內(nèi)的直線條數(shù)減少到有限條，是最佳選擇，那么平面內(nèi)的直線有無數(shù)條，怎么減少呢？由定義前面的感知過程可知，同一方向的直線都垂直，也就是說，同一方向只取一條線，那么取哪條直線更直觀？如：圖4中取哪條直線？(取與直線l垂直的直線m，且P∈m∩l)

(3)這樣平面α中的直線已經(jīng)減少到過P點(diǎn)的不同方向的直線，但仍有無數(shù)條.那么不同方向的直線，仍有無數(shù)條，又怎么再減少直線條數(shù)呢？如果不能再減少，我們能不能反向思考一下，從這些不同方向的直線中取一條直線開始嘗試操作，然后依次增加一條直線，直到能夠判定線面垂直為止.那么，我們從先取一條直線與直線l垂直開始，請同學(xué)們思考或把課桌面看成一個(gè)平面，把手中的筆看成一條直線，操作一下.

(4)既然面內(nèi)一條直線不行，那么過點(diǎn)P再增加面內(nèi)一條直線呢？我來做一個(gè)操作試驗(yàn)：

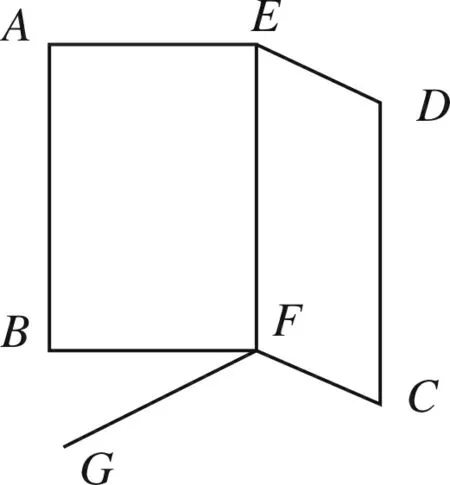
圖5

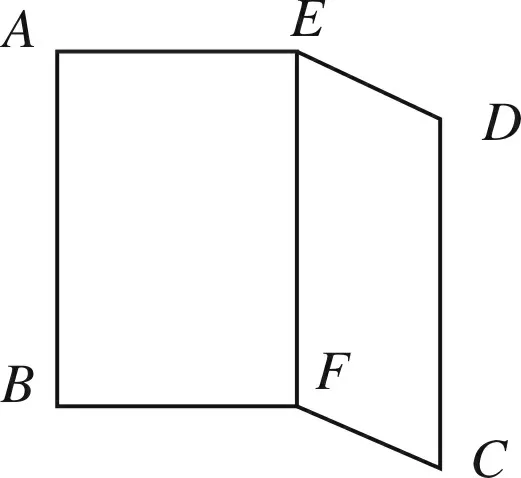
圖6

請同學(xué)們拿出準(zhǔn)備好的一塊矩形紙片，如圖所示，過矩形兩對邊上分別取兩邊的中點(diǎn)E、F，過E、F兩點(diǎn)的直線折疊，得到折痕EF，易知EF⊥BC,即EF⊥FB,EF⊥FC.沿著折痕EF翻折，使得紙片豎起放置在桌面上(BF、FC與桌面接觸)，如下圖5所示.觀察并思考：①在桌面上放一張白紙，放在矩形折紙的下面，過點(diǎn)F任意畫一條直線FG,折痕所在的直線EF與直線FG垂直嗎？(如圖6)②請大家把書沿著書脊打開，不要展平，站立放置，即封面與封底兩面如圖5放置，看看其他頁碼的長方形頁面與桌面接觸的邊與桌面是否完全吻合？說明什么？③根據(jù)定義，折痕EF所在的直線與桌面所在的平面垂直嗎？

(5)你能夠準(zhǔn)確說出直線與平面垂直的判定方法嗎？“兩條相交直線”改為“兩條平行直線”是否可以？是否可以增加至三條直線呢？

設(shè)計(jì)意圖問題(1)回顧由線面平行的定義到線面平行判定的探究過程，思考由線面垂直的定義到線面垂直判定的探究過程，看看有沒有可以借鑒的思考過程和方法，通過比較，提取對線面垂直判定有作用的“減少面內(nèi)直線的條數(shù)”是合適的思考問題的方法；問題(2)由定義的感知，學(xué)生已經(jīng)知道，同一方向的直線，只要一條垂直就可以了，這樣減少了許多同方向的直線.那么同一方向取那一條好呢？因?yàn)閷W(xué)生最先學(xué)習(xí)的是共面相交，當(dāng)然，直線m是最好的選擇.這也為判定定理中的“面內(nèi)兩直線相交”打下伏筆；問題(3)由同一方向的直線，在平面內(nèi)取與直線l相交的直線，那么過交點(diǎn)F的直線仍有無數(shù)條.繼續(xù)減少直線條數(shù)已經(jīng)沒辦法完成，讓學(xué)生反向思維，從最少的一條直線出發(fā)，逐步增加直線條數(shù)，直線符合為止.先讓學(xué)生操作，容易判定面內(nèi)一條直線與直線l垂直是不行的；問題(4)是讓學(xué)生“操作確認(rèn)”判定定理的過程.先在確定面內(nèi)兩條相交線BF和FC,再讓學(xué)生過點(diǎn)F畫一直線，度量或利用三角板的直角判定所畫直線是否與直線EF垂直，為了進(jìn)一步判定與面內(nèi)不同方向的直線垂直，讓學(xué)生利用課本“直立”操作，觀察其他頁面的矩形的下面的一邊是否在桌面內(nèi)，學(xué)生得出不同方向的許多直線都與直線EF垂直，從而初步得出判定定理；問題(5)讓學(xué)生明確問題(4)得到的方法合理后，為了加深對“兩線相交”的理解和記憶，設(shè)計(jì)“兩線平行”是否可以，也是對學(xué)習(xí)定義前“平行直線”只要一條垂直，其他直線一定垂直，所以平行直線條數(shù)再多也“沒用”.同時(shí)，提問是否可以再加一條直線的問題，旨在讓學(xué)生體會這種方法的簡潔性和嚴(yán)謹(jǐn)性.

直線與平面垂直的判定定理

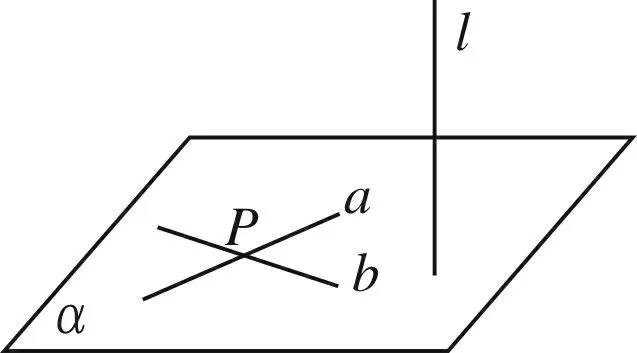
如果一條直線和一個(gè)平面內(nèi)的兩條相交直線都垂直，那么該直線與此平面垂直.

圖形語言表示：

符號語言表示：

2）放眼全球，重點(diǎn)選擇。在埃克森美孚公司的七大油氣戰(zhàn)略區(qū)中，北美、南美、大洋洲是核心戰(zhàn)略區(qū)，其次是歐洲和非洲，而亞洲及中東并不具有重要位置。中東以資源豐富且優(yōu)質(zhì)著稱，埃克森美孚并沒有太多涉足，僅進(jìn)入卡塔爾、阿聯(lián)酋、伊拉克等少數(shù)幾個(gè)國家，也不占據(jù)主導(dǎo)地位。亞洲也是諸多國際石油公司早期進(jìn)入并視為核心的戰(zhàn)略區(qū)，埃克森美孚除了在哈薩克斯坦與雪佛龍、殼牌等大石油公司聯(lián)合作業(yè)參股田齊茲、卡沙甘等少數(shù)幾個(gè)大項(xiàng)目外，只進(jìn)入印尼、馬來西亞等少數(shù)國家，存在感不強(qiáng)。埃克森美孚非常看好俄羅斯北極地區(qū)，但隨著美國對俄羅斯實(shí)施能源制裁，埃克森美孚不得不撤出了其在俄羅斯北極龐大的勘探項(xiàng)目。

a?α,b?α,a∩b=P,l⊥α,l⊥b?l⊥α.

4.3 應(yīng)用

(1)前面多次學(xué)習(xí)到“一組平行直線”在不考慮位置不同的情況下，可以看作“一條直線”或“取其中的一條直線”.

我們在“2.2.3直線與平面平行的性質(zhì)”中學(xué)習(xí)了例2：平面外的兩條平行線，一條平行于平面，則另一條直線也和這個(gè)平面平行.

a∥α,b?α,a∥b?b∥α.

請大家思考一下，在直線與平面垂直中是否有類似的命題？(兩條平行線，一條垂直于平面，則另一條直線也和這個(gè)平面垂直.)此命題是否正確？

設(shè)計(jì)意圖通過此問，培養(yǎng)學(xué)生類比思維的習(xí)慣，并讓學(xué)生形成合理而且完善的認(rèn)知結(jié)構(gòu).同時(shí)，進(jìn)一步加深：一組平行線在只考慮方向的情況下，可以只考慮其中的一條直線即可.也為下面例題的出現(xiàn)進(jìn)行合理的過渡，并為例題的解決打下基礎(chǔ).

(2)例題

證明

方法一：由a⊥α，得：a垂直于α內(nèi)所有直線，

又因?yàn)閍//b，所有b垂直于α內(nèi)所有直線

所以b⊥α.

方法二：在平面α內(nèi)作兩條相交直線m、n，

因?yàn)橹本€a⊥α，

根據(jù)直線與平面垂直的定義知：a⊥m,a⊥n.

又因?yàn)閍//b，所以b⊥m,b⊥n，

又因?yàn)閙?α，n?α，m、n是兩條相交直線，所以b⊥α.

設(shè)計(jì)意圖讓學(xué)生初步體會：運(yùn)用直線與平面垂直的定義和判定定理解決問題的思維方式，掌握應(yīng)用線面垂直判定定理的條件與書寫格式.

4.4 結(jié)課

(1)本節(jié)課你學(xué)會了哪些知識？

(2)定義到判定定理是怎樣得到的？

(3)判定“直線與平面垂直的方法”有兩個(gè)(定義法和判定定理法)，判定定理法要注意什么？(“面內(nèi)”、“兩條相交直線”).

設(shè)計(jì)意圖總結(jié)本節(jié)課的兩個(gè)知識點(diǎn)(線面垂直的定義和判定)和知識發(fā)生發(fā)展的思維過程，重組學(xué)生的認(rèn)識結(jié)構(gòu)并使得新認(rèn)知結(jié)構(gòu)具有開放性.

其上，是對多次進(jìn)行賽課內(nèi)容：《直線與平面垂直的判定》，進(jìn)行的個(gè)人設(shè)計(jì)，僅供大家參考.目的是讓各位同仁明白：我們應(yīng)該花大氣力整合和改造教材中的知識，添加自己的處理內(nèi)容，形成合理的知識結(jié)構(gòu)，使得課堂教學(xué)的教學(xué)設(shè)計(jì)契合學(xué)生的認(rèn)知水平.這樣的教學(xué)設(shè)計(jì)，加上教師課堂教學(xué)中合理而機(jī)智的引導(dǎo)，才能夠最大化地發(fā)揮學(xué)生潛能，使得學(xué)生“迷”上數(shù)學(xué)，這才是我們孜孜以求的“境界”.