基于數字化齒面的弧齒錐齒輪柔性多體接觸動力學分析
姚廷強, 姚 龍, 王學軍, 王立華
(昆明理工大學 機電工程學院,昆明 650093)
弧齒錐齒輪被廣泛應用于汽車和航空航天領域。弧齒錐齒輪正朝著高速、高載荷質量比和高可靠性的方向發展,其動態嚙合接觸傳動特性對整機性能有著重要的影響,也是傳動誤差規律、動態設計和可靠性分析的基礎[1-2]。弧齒齒面的幾何形狀和加工方法復雜,難以獲得弧齒齒面的解析解。目前,弧齒齒面的數字化建模方法應用較為廣泛,一般是根據齒輪加工原理和齒面嚙合理論,建立弧齒齒面方程,運用MATLAB計算弧齒齒面的數字化坐標點,再運用NURBS曲面擬合重構精確的弧齒齒面模型。Litvin等[2-4]提出弧齒錐齒輪的局部綜合法,討論了三齒有限元接觸分析方法。Cheng等[5]根據齒輪嚙合原理,運用精確幾何模型分析準雙曲面錐齒輪傳動振動特性。Zhang等[6]采用三次樣條擬合弧齒齒面,提出輪齒接觸的數值分析方法。Sheveleva等[7]提出了螺旋錐齒輪嚙合接觸的接觸痕、傳動誤差和接觸壓力分布的數值算法。汪中厚等[8]提出一種基于高精度數字化真實齒面的螺旋錐齒輪齒面接觸分析方法。唐進元[9],劉光磊[10],郭偉超[11]運用MATLAB平臺計算弧齒齒面的數字化數據點,分別建立了含有過渡曲面的弧齒錐齒輪三維模型和精確輪齒有限元模型。蘇進[12],劉光磊[13],Lin[14]基于弧齒錐齒輪齒面三坐標測量網格點數據,重構離散數值弧齒齒面,分析了弧齒錐齒輪傳動誤差規律。張金良等[15]在ANSYS平臺下建立了弧齒錐齒輪多齒模型,分析了多齒對接觸下齒根接觸應力的變化規律。唐進元等[16-17]運用ABAQUS和LS-DYNA平臺,以動態加載接觸分析有限元方法為基礎,考慮慣性載荷和動態嚙合關系,建立弧齒錐齒輪有限元模型,分析了嚙合接觸變化規律。汪中厚等[18-19]運用ABAQUS建立真實齒面的螺旋錐齒輪有限元模型,進行了傳動誤差分析。侯祥穎[20]運用數值化方法計算結點坐標,提出基于高精度建模的有限元分析方法。方崇德,鄧效忠[21],高建平等[22],侯祥穎等[23]開展考慮邊緣接觸的弧齒錐齒輪承載接觸分析。姚廷強等[24]采用Litvin的局部綜合法計算得出弧齒齒面的數字化坐標點,運用三角網格方法,重構弧齒齒面模型,進行弧齒齒面動態接觸多剛體動力學分析。
多數文獻以靜態或準靜態力學分析方法為基礎,建立單對或多對弧齒嚙合傳動的有限元模型,進行弧齒TCA輪齒接觸分析和LTCA承載接觸分析。這些方法未考慮弧齒錐齒輪的全齒模型,質量和慣量特性不完整,計算結果不能完全反映在弧齒齒面動態接觸狀態下弧齒錐齒輪的傳動特性。考慮完整弧齒齒輪彈性變形和精確弧齒齒面三維動態接觸特性,計算弧齒齒面嚙合傳動規律和邊緣接觸分析,成為弧齒錐齒輪系統柔性多體動力學亟待解決的研究問題。
1 弧齒錐齒輪齒面建模方法
1.1 弧齒齒面的空間離散點
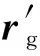
(1a)
(1b)
式中:rg=Ru±Pω2/2為常數刀齒半徑;Ru為刀盤公稱半徑;Pω2為刀頂距;αg為刀具齒形角;sg、θg為刀具切削錐面的坐標參數。“±”表示對應加工弧齒齒面的凹凸面。
將刀盤坐標系下的式(1a)和式(1b),通過一系列坐標變換至齒輪體坐標系下,可得弧齒齒輪的齒面方程rg和法向矢量ng。
(2a)
(2b)
式中:Aru為刀盤坐標系到搖臺坐標系的變換矩陣;Amr為搖臺坐標系到機床坐標系的變換矩陣;Aam為機床坐標系到輔助坐標系的變換矩陣;Aba為輔助坐標系到節錐坐標系的變換矩陣;Agb為節錐坐標系到齒輪體坐標系的變換矩陣。
結合齒面嚙合方程可得
ng·vg=0
(3)
式中:vg為被加工齒輪與切削刃在切削點的相對速度。
由弧齒齒面方程式(2a)和嚙合方程式(3)可求得以θg、ψg描述的齒面方程。
(4)
式中:xg、yg和zg為在齒輪體坐標系下弧齒齒面離散點的坐標分量。
運用MATLAB編程計算弧齒齒面的離散點的計算結果,如圖1所示。
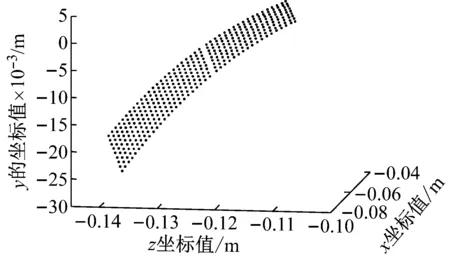
圖1 弧齒齒面空間離散點
1.2 弧齒齒面的法向矢量
以Matlab計算的數字化坐標點為弧齒齒面的表面結點,運用Hypermesh重構弧齒齒面,以六面體單元劃分弧齒錐齒輪,建立真實柔性體有限元模型。將弧齒錐齒輪的單元和結點數據輸出至ADAMS/MaxFlex,基于浮動參考坐標法和有限單元法的小變形柔性體建模方法[25],運用浮動坐標系下的相對結點坐標來直接描述弧齒錐齒輪的彈性變形。選取弧齒齒面的單元表面和相鄰4個結點,構成四邊形面片單元,進而由四邊形面片單元集合構成弧齒齒面的接觸塊,實現多柔性體、多弧齒面的動態接觸搜索計算。圖2為弧齒齒面的四邊形面片網格模型。
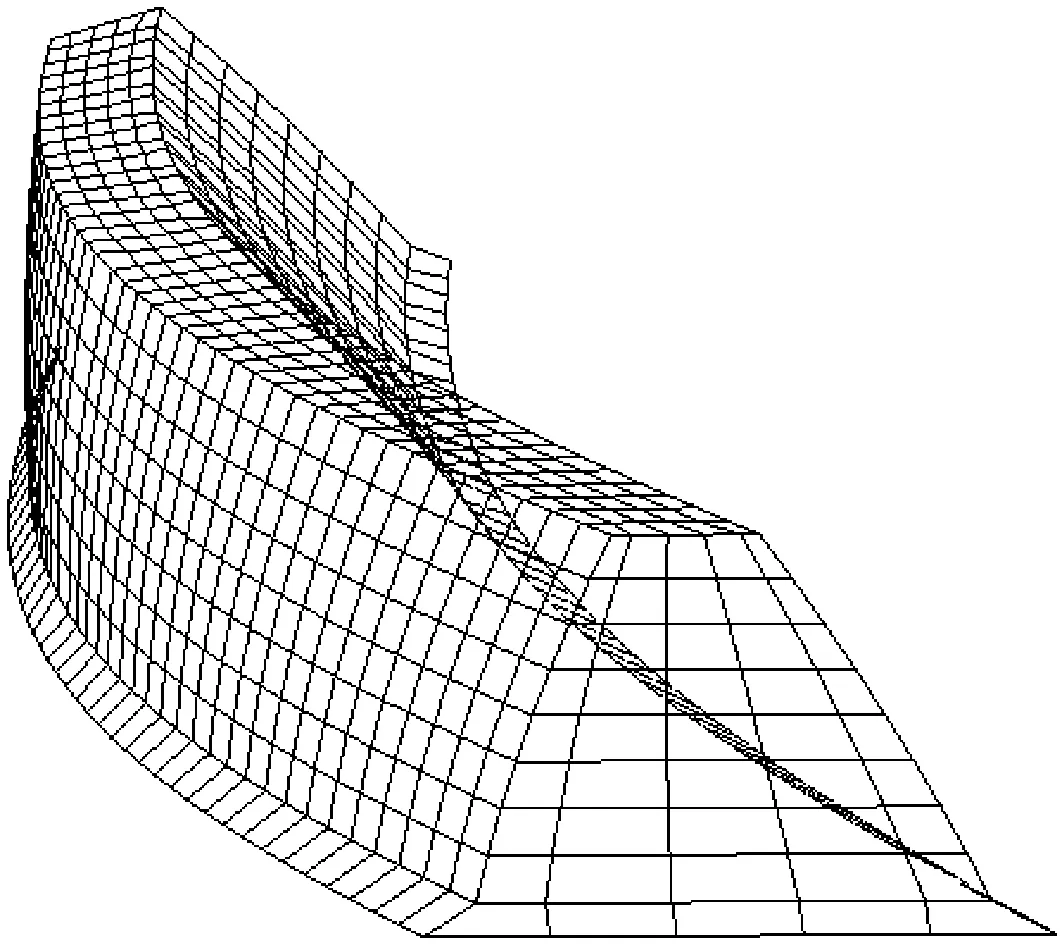
圖2 弧齒齒面的四邊形面片單元模型
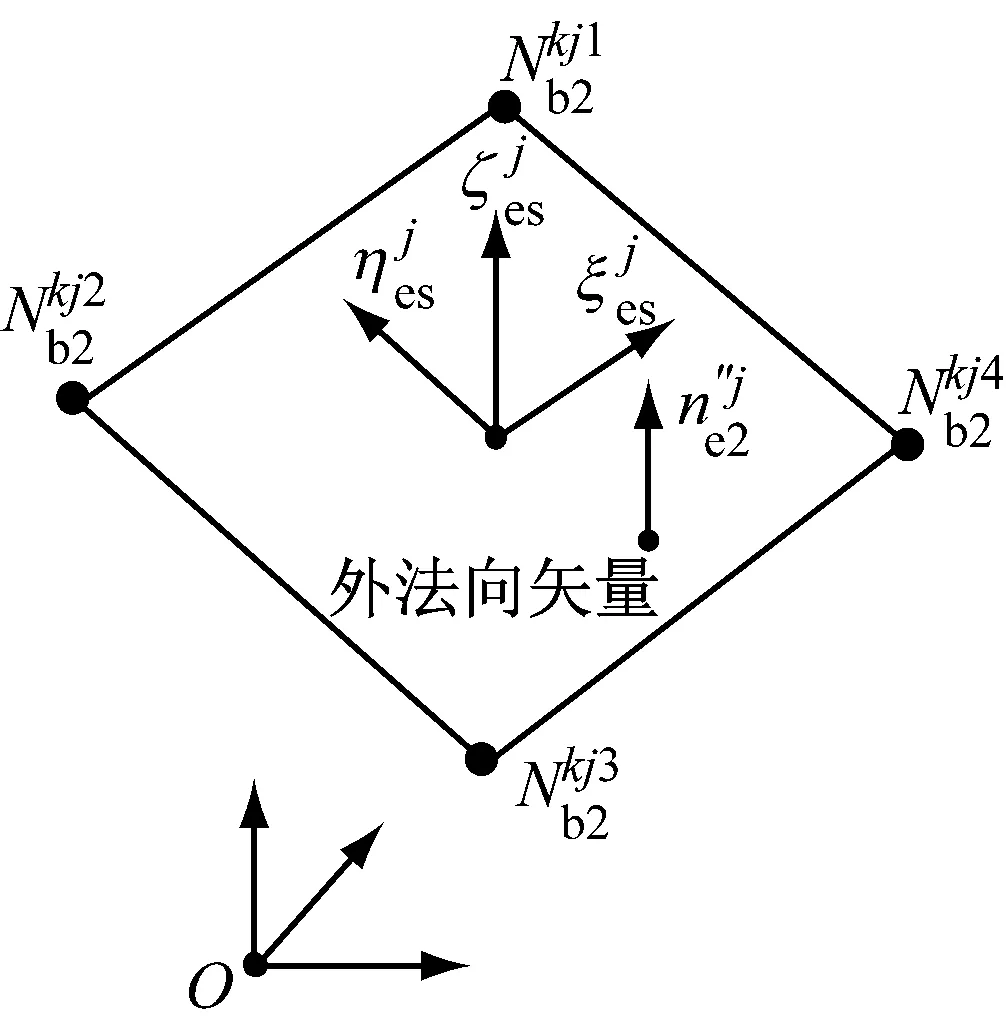
圖3 四邊形面片單元的外法向矢量
(5)
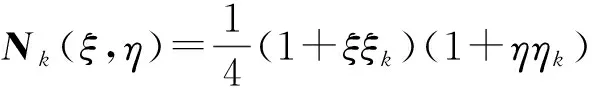
弧齒齒面的四邊形面片單元的外法向矢量為
n″=x″(ξ,η)ξ×x″(ξ,η)η
(6)
式中:x″(ξ,η)ξ,x″(ξ,η)η為位置矢量x″(ξ,η)關于局部參數ξ,η的偏導數,其物理意義是四邊形面片單元的切向矢量。
由此可求得四邊形面片單元的單位外法向矢量和單位切向矢量分別為
(7a)
(7b)
(8)
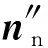
基于弧齒齒面的四邊形面片接觸塊,編制自定義程序計算四邊形面片單元中心的單位外法向矢量,提高弧齒錐齒輪柔性多體動態接觸的計算效率。圖4為弧齒齒面的四邊形面片單元的中心外法向矢量示意圖。

圖4 四邊形面片單元的中心外法向矢量
2 弧齒齒面的動態接觸力學模型
2.1 弧齒齒面的動態接觸搜索方法
由參考系移動坐標、轉動坐標和結點坐標來描述的柔性錐齒輪i的單元j中任一點的位置矢量的一般形式為[25]
(9)
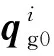
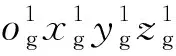
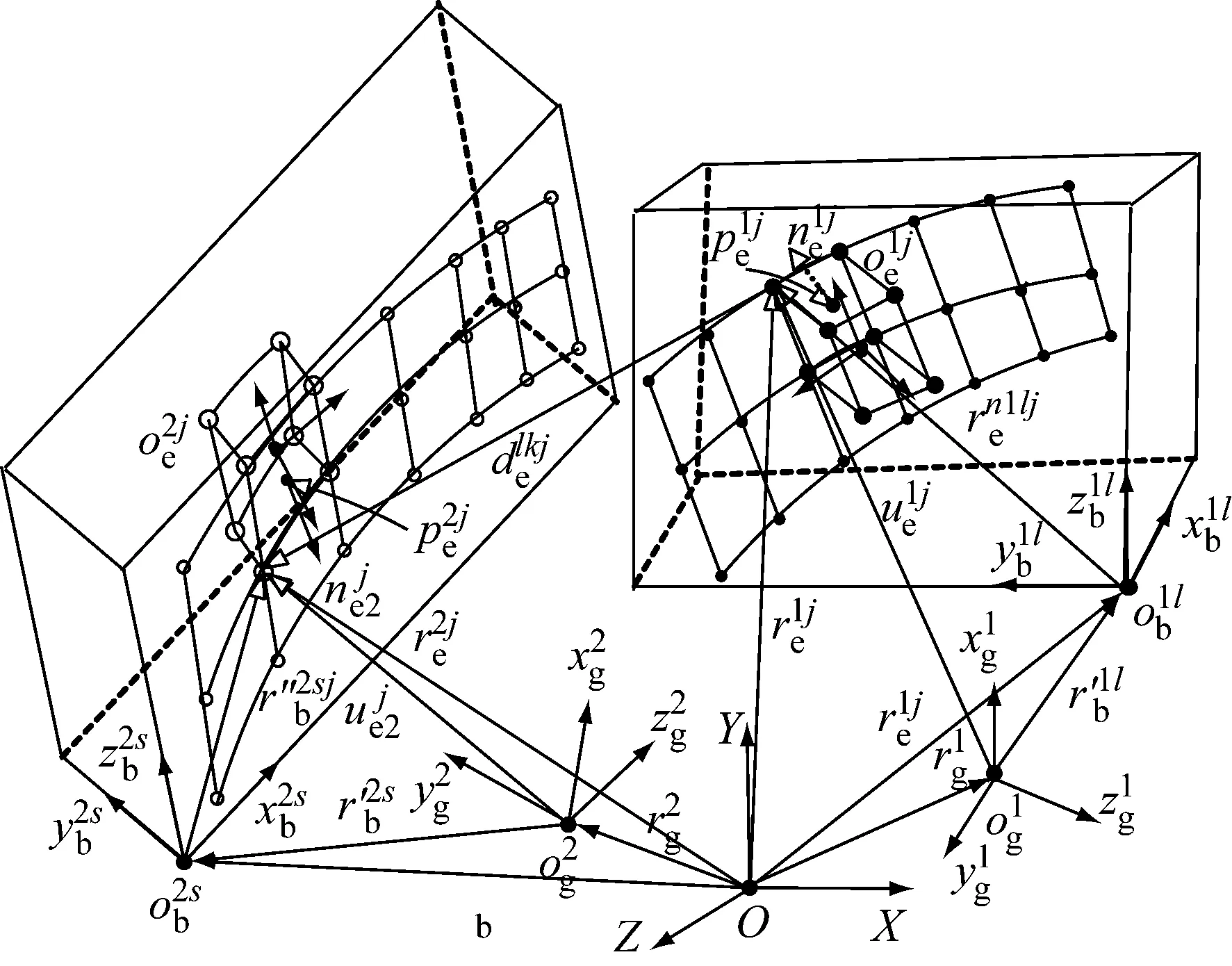
圖5 弧齒齒面的動態接觸關系
在絕對坐標系下柔性錐齒輪的弧齒齒面的立方體包圍坐標原點的位置矢量為
(10)
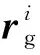
在慣性坐標系下主從弧齒齒面上的各結點的位置矢量可由包圍盒坐標系下的相對位置矢量來描述。
(11)

在全域接觸搜索過程中,基于弧齒齒面的立方體包圍盒技術,運用式(10)對立方體剛體及其立方體單元進行搜索計算,確定發生接觸的立方體。基于弧齒齒輪的小變形假設,運用式(9)和式(11)計算可能發生接觸的主、從錐齒輪弧齒齒面上的少量從點和目標單元面。
在局部接觸搜索過程中,弧齒嚙合齒面的動態接觸實質上是從結點-目標四邊形面片單元的動態接觸,由此構成結點-目標面的主從搜索方法。因此,主從搜索方法[26]僅對可能發生接觸的從點和目標單元面進行搜索計算,以進一步確定發生接觸的從點和目標單元面。由式(9)和圖5可知,主動輪g1的弧齒齒面的四邊形面片單元上的從結點與從動輪g2的弧齒齒面的四邊形面片單元上的主結點的相對位置矢量為
(12)
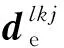
在局部接觸搜索過程中,主從搜索方法運用式(12)計算主、從結點之間距離,確定弧齒齒面上距離從結點最近的主結點,進而確定從動輪的弧齒齒面上包含該主結點的所有四邊形面片單元。
圖6為從結點到目標單元面的法向距離。從結點到目標單元面的法向距離等于從結點與目標單元面內的任意一點(此處選擇最近的主結點)所構成的向量在外法向矢量方向上的投影長度。因此,在目標單元面的局部坐標系下從結點與主結點的最近的相對位置矢量為
(13)
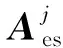
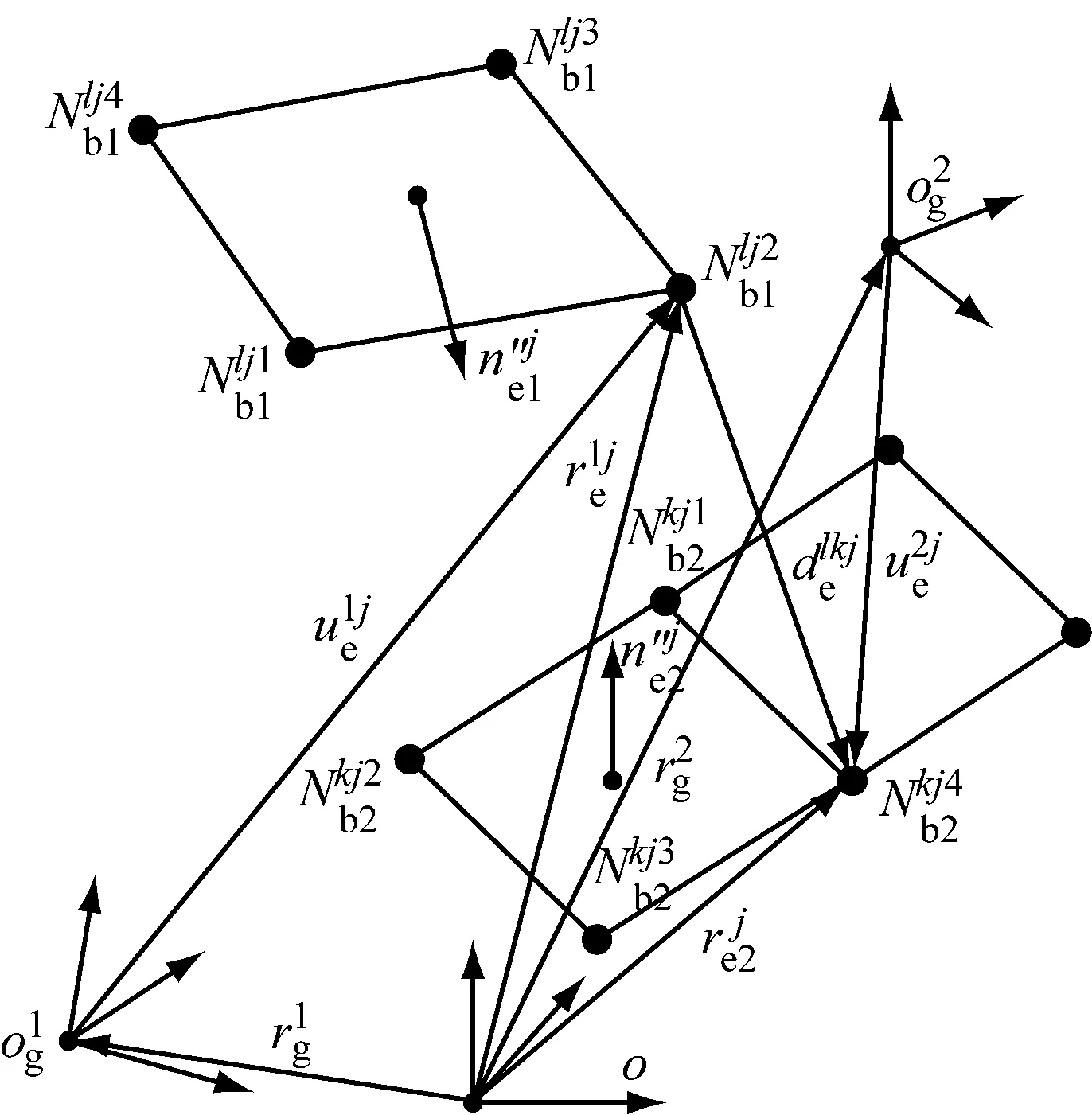
圖6 從結點到目標單元面的法向距離
將式(13)沿著目標單元面的單位外法向矢量方向投影,計算從結點到包含最近主結點的所有目標單元面的最近法向距離,即得從結點-目標單元面的法向間隙量為
(14)
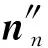
(15)
式中:δ為從結點與目標單元面的接觸變形。
2.2 弧齒齒面的接觸力計算模型
運用罰函數法計算弧齒齒面的法向接觸力,同時考慮嚙合齒面的阻尼作用和摩擦作用,建立弧齒齒面的遲滯法向接觸力模型。由式(15)的接觸彈性變形可得弧齒齒面間的法向接觸力顯示表達式為
(16)
式中:Fgn為弧齒齒面的四邊形面片單元的法向接觸力,Kgc和Cgc分別為弧齒齒面弧齒中點節圓處的平均Hertz接觸剛度和阻尼[24]。

圖7 摩擦因數與相對速度關系
根據庫倫摩擦定律,弧齒齒面之間的摩擦力與法向接觸力間的關系為
Fgμ=μ(v)Fgn
(17)
圖7為弧齒齒面的接觸過程中摩擦因數與相對速度的關系,則摩擦因數為
(18)
式中:havsin(…)半正弦函數描述摩擦因數從靜摩擦因數到動摩擦因數的平滑非線性變化,vgτ為弧齒齒面中發生Hertz接觸作用時所對應的接觸靶點處的相對切向速度,由從結點與目標單元面在接觸對處切線方向的速度分量來計算。
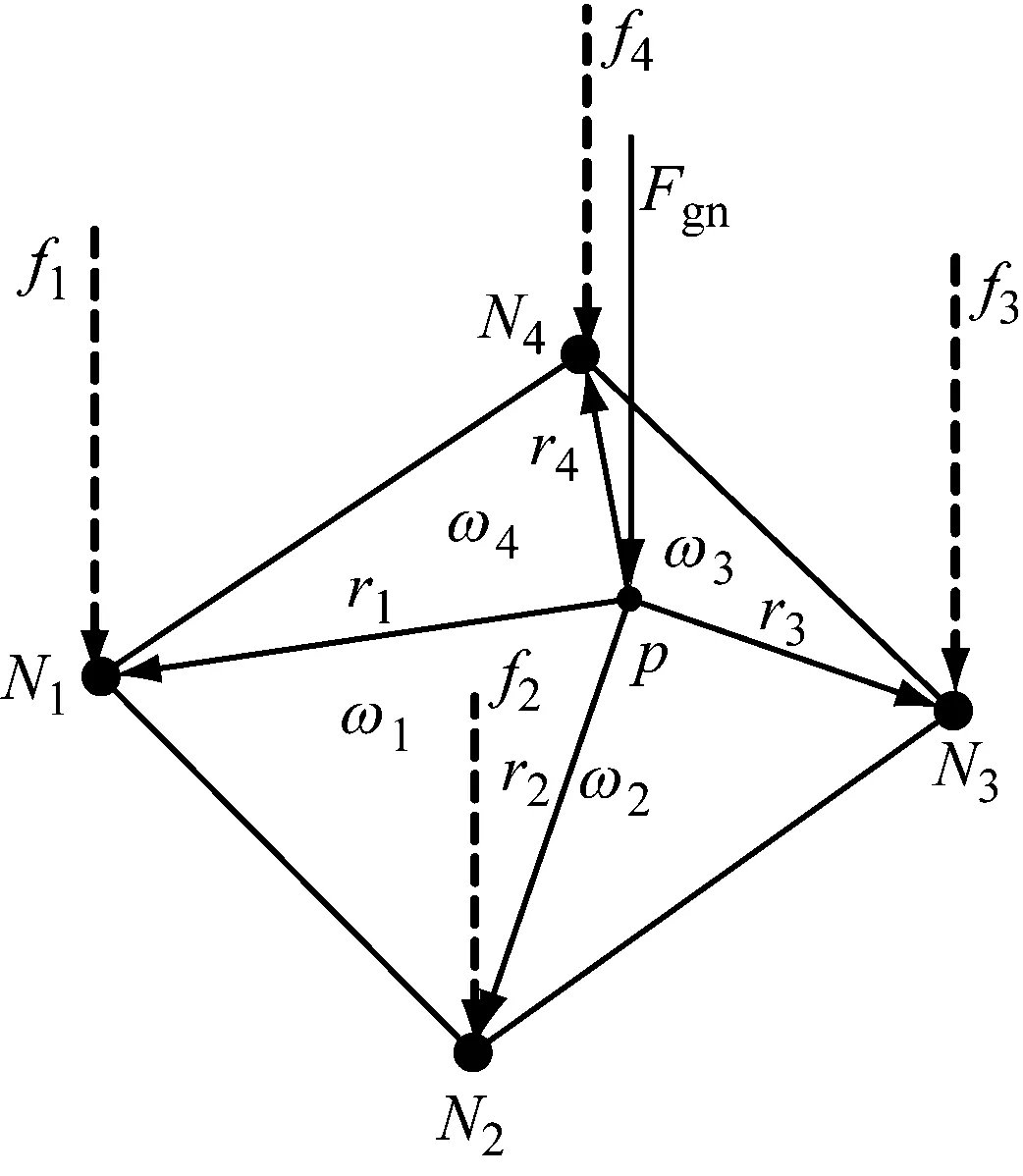
圖8 目標單元的法向接觸力分配關系
圖8為目標單元的法向接觸力分配關系。采用從結點在目標單元面的投影靶點p與四邊形面片的4個結點構成的4個不同面積的三角形的線性插值方法,將目標單元面上的法向接觸力分配給四個結點,獲得結點的法向接觸力分量[27]。
各結點處的法向接觸力的分量力滿足:
(19)
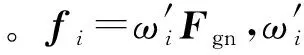
2.3 弧齒錐齒輪柔性多體接觸動力學模型
柔性錐齒輪系統的動力學方程為
(20)
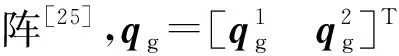
基于精確弧齒齒面模型和弧齒輪真實結構的柔性體有限元模型,基于ADAMS/MaxFlex多體動力學仿真平臺,基于弧齒齒面的四邊形面片接觸塊,實現弧齒齒面的多界面動態接觸搜索算法和遲滯法向接觸力計算,分析弧齒錐齒輪的多柔性體、多界面動態接觸力學特性。
3 柔性弧齒錐齒輪動力學計算實例
3.1 弧齒錐齒輪傳動特性分析
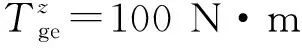
圖9和圖10分別為剛性弧齒輪和柔性弧齒輪的嚙合傳動過程中,從動齒輪的角速度和轉角誤差的變化規律。分析可知,剛性弧齒錐齒輪傳動的轉速波動幅度比柔性弧齒錐齒輪的要大。考慮弧齒錐齒輪的結構彈性變形時,從動齒輪轉速以3 000 r/min為中心,以12 r/min幅值波動,幅度相對較小,轉角動態誤差較小,且成周期性變化,傳動更加平穩。圖中放大區域為0.02~0.03 s半個嚙合周期內(T/2=0.01 s),由單齒嚙合時間Tz=0.001知,有10對相鄰弧齒嚙入和嚙出,受嚙合頻率的影響,角速度出現10個波峰波谷的周期變化規律。計算結果說明彈性變形對弧齒錐齒輪的傳動特性有重要的影響,較為真實地表現了弧齒錐齒輪的傳動特性。
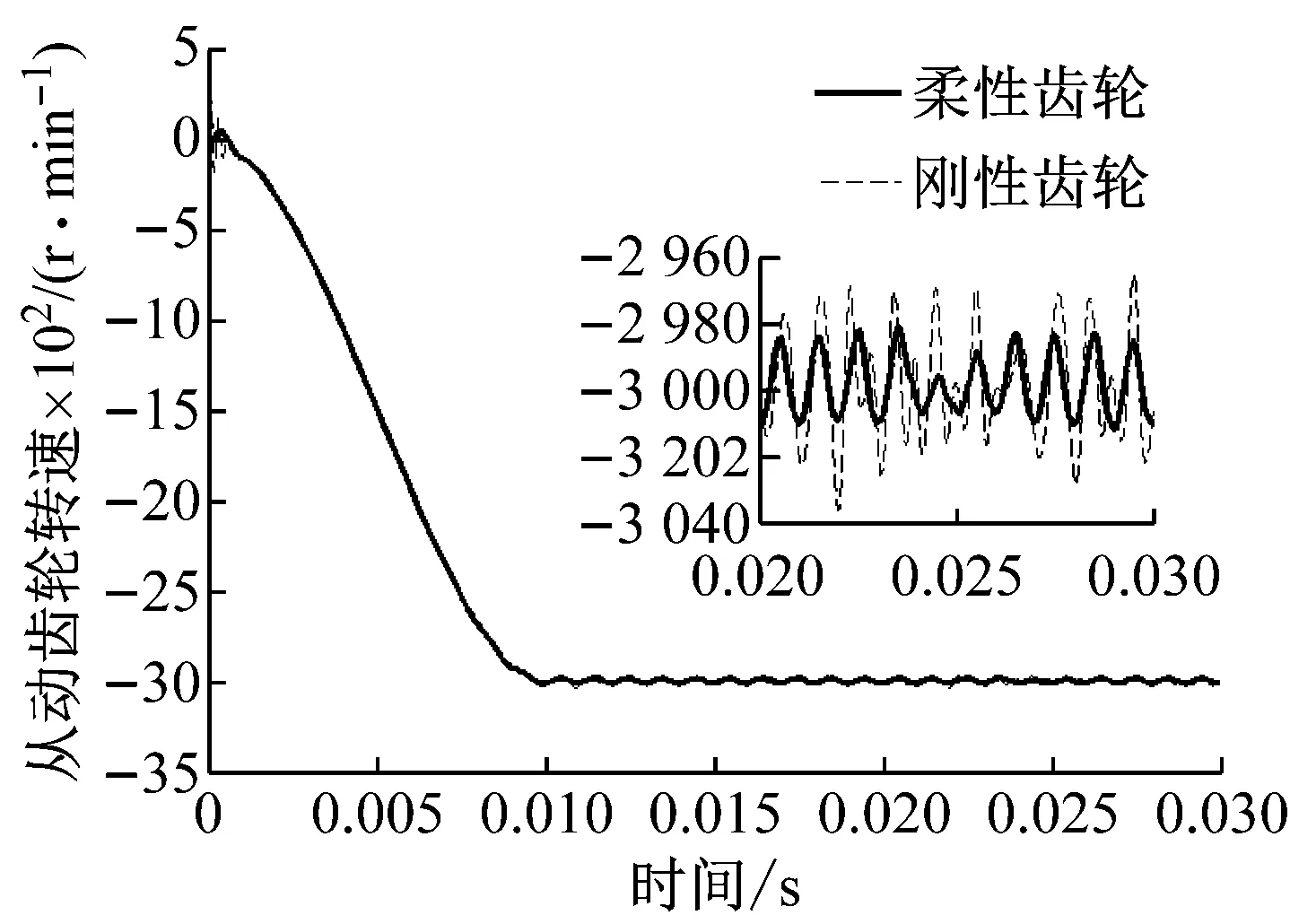
圖9 從動齒輪的角速度
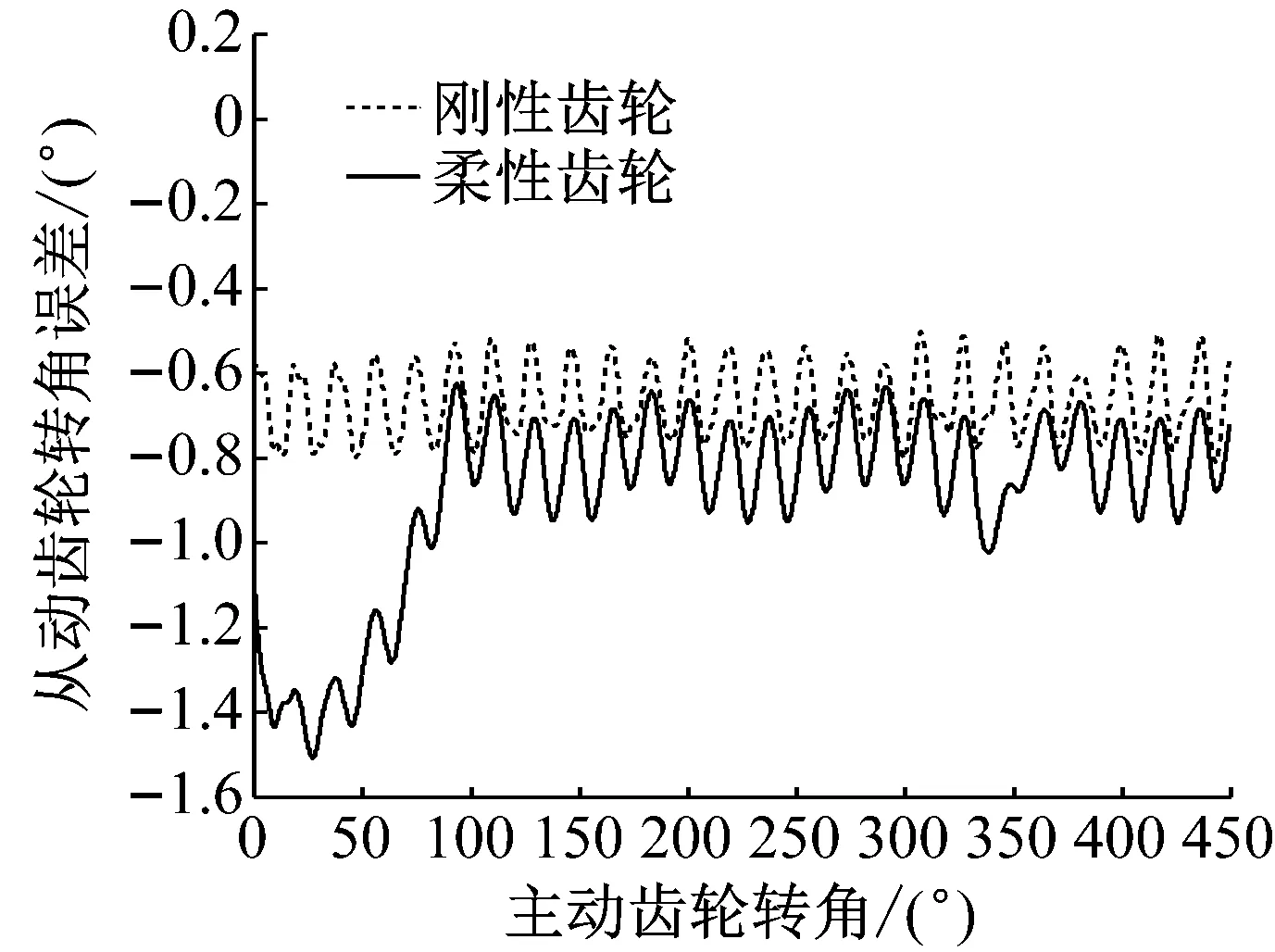
圖10 從動齒輪的轉角動態誤差
圖11分別為剛、柔性弧齒輪嚙合傳動過程中,相鄰弧齒嚙合齒面的動態接觸力的變化規律。弧齒錐齒輪傳動過程中,同時有相鄰3對輪齒參與承載嚙合傳動,當有弧齒逐漸嚙入或嚙出時,相鄰弧齒的動態接觸力會表現出波峰或波谷的變化規律。由于柔性弧齒輪傳動的轉速波動較小,單齒嚙合承載時間短于剛性輪齒,柔性弧齒嚙合齒面存在明顯的弧齒齒頂邊緣接觸(圖13),使得柔性弧齒齒面的嚙合接觸力比剛性輪齒的要大。圖12為從動弧齒錐齒輪的約束反力。柔性弧齒錐齒輪嚙合傳動過程中,由于柔性弧齒存在明顯的邊緣接觸,約束位置處的合力和各方向分量力均呈周期性的變化規律,合力(FM)、徑向分量力(FX和FY)和軸向分量力(FZ)的波動幅值大于剛性齒輪的。柔性齒輪的徑向分量力FX的數值是以剛性齒輪的徑向分量力FX為最小值,以2 180 N成倍的幅度周期波動,而柔性齒輪的徑向分量力FY的數值是以剛性齒輪的徑向分量力FY為最大值,以1 850 N成倍的幅度周期波動。結果表明考慮彈性變形和弧齒齒面動態接觸關系的完整弧齒錐齒輪更真實地模擬齒輪傳動特性。弧齒錐齒輪的剛體假設方法忽略弧齒錐齒輪的彈性變形,會低估弧齒齒面的動態接觸力和齒輪系統的約束反力,從而影響弧齒錐齒輪和滾動軸承的可靠性分析和疲勞壽命的計算結果。
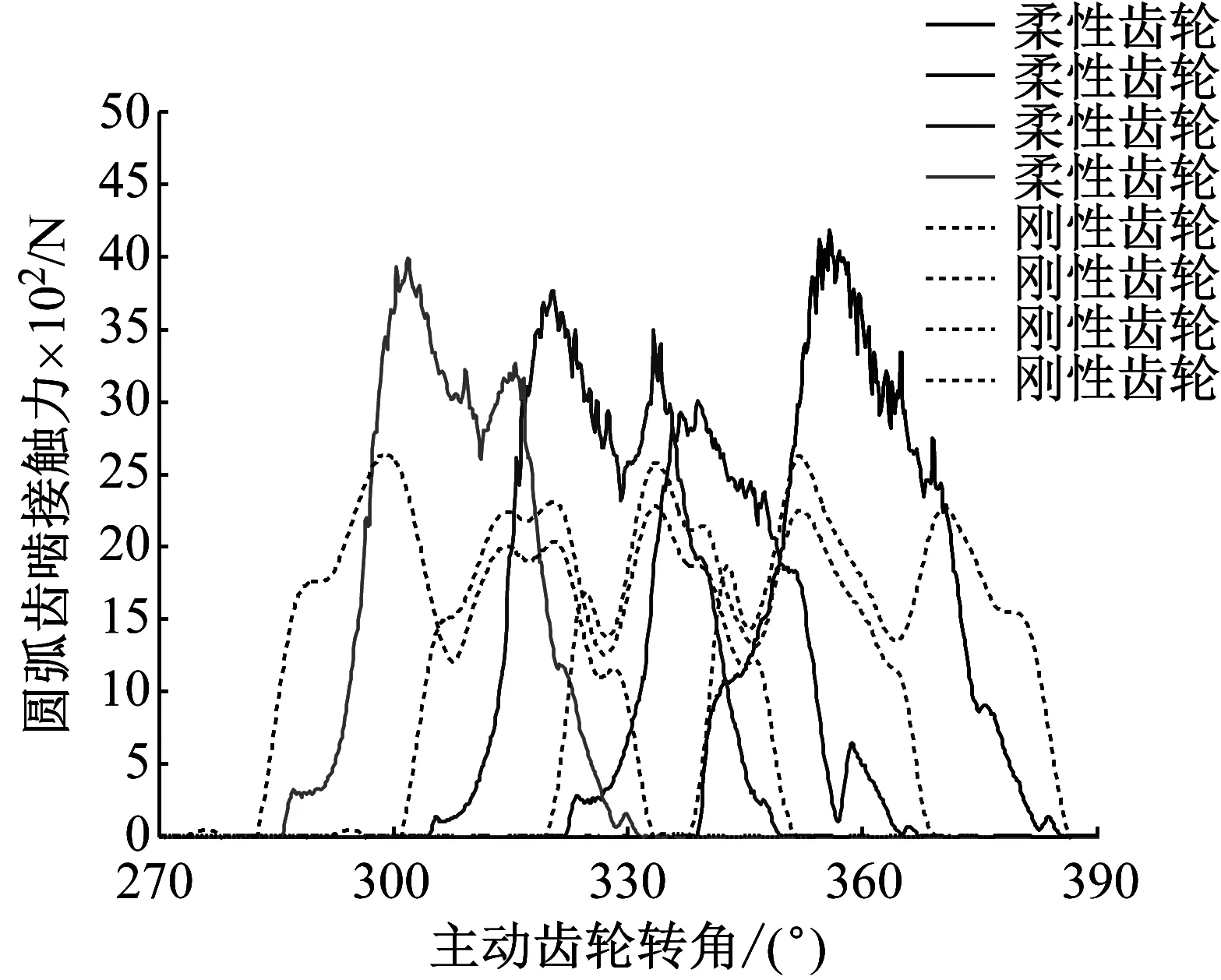
圖11 相鄰弧齒嚙合齒面的動態接觸力
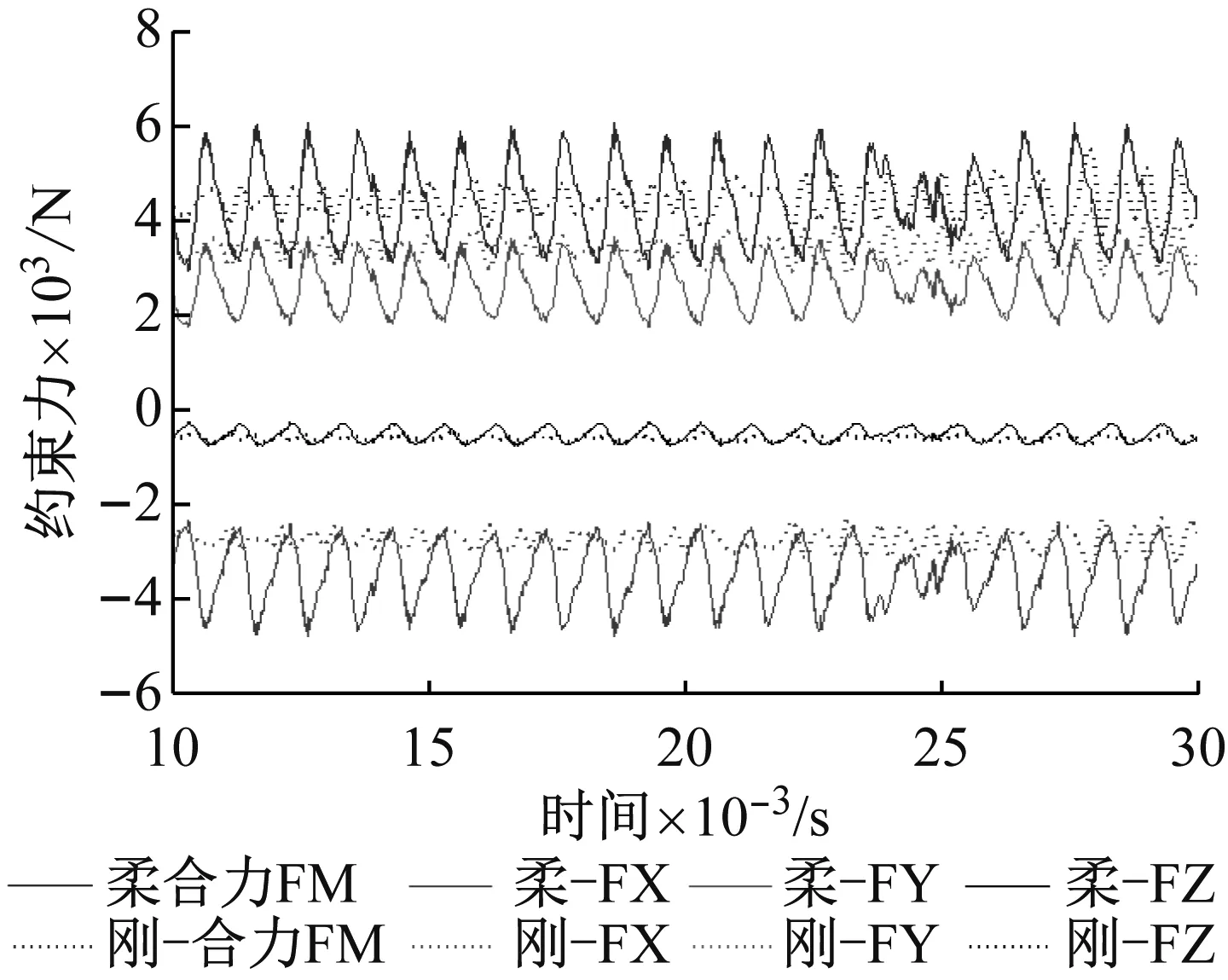
圖12 從動齒輪的約束反力
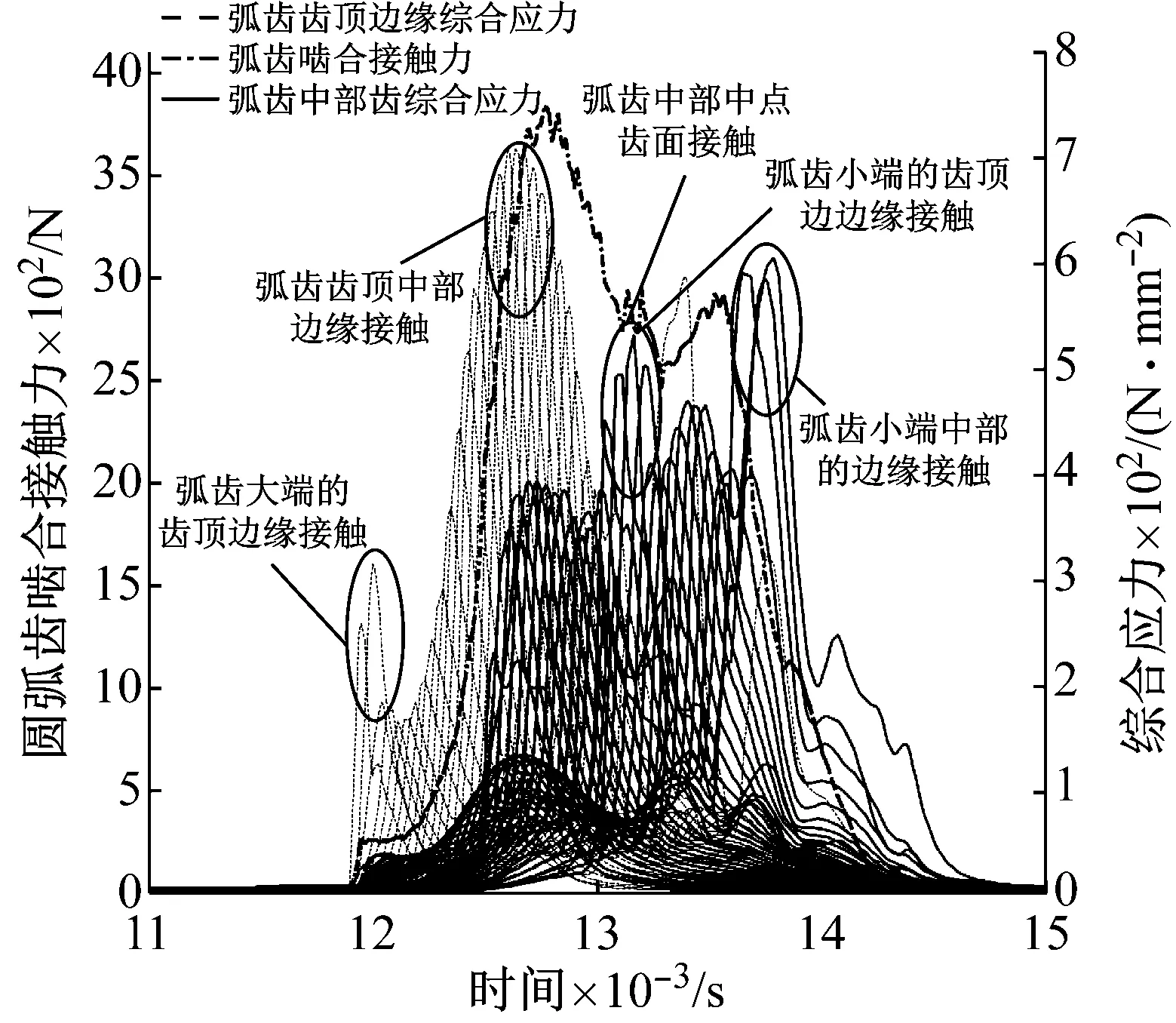
圖13 弧齒齒面的嚙合接觸力和綜合應力
Fig.13 Contact force and Von Mises stress of gear tooth surface
圖13為弧齒齒面嚙合接觸力、齒頂邊緣各結點的綜合應力和齒面中部各結點的綜合應力。分析可知,主動輪的凹面和從動輪的凸面為弧齒嚙合齒面,齒面從大端嚙入,小端嚙出。對比分析圖11和13可知,考慮圓弧齒的結構彈性變形影響,弧齒嚙合傳動過程中,柔性弧齒錐齒輪存在明顯的齒頂邊緣接觸和弧齒小端的邊緣接觸,弧齒齒頂邊緣接觸對齒面綜合應力和齒面嚙合接觸力有著重要的影響。當齒頂邊緣或弧齒小端發生接觸時,由于承載區域較小,弧齒齒面存在較大的綜合應力,尤其是齒頂中部發生邊緣接觸時的綜合應力數值較大。當齒頂中部邊緣和齒面中部同時發生接觸時,弧齒齒面嚙合接觸力達到最大值,隨著齒頂邊緣接觸逐漸退出嚙合,接觸力逐漸減小,此時弧齒齒面嚙合接觸力與剛性齒輪的齒面嚙合接觸力大小接近。
3.2 弧齒齒面的動態接觸特性
圖14為弧齒齒面的綜合應力云圖。圖16為弧齒錐齒輪嚙合齒面的最大綜合應力的變化規律。在啟動加速階段,弧齒嚙合齒面出現較大的應力值,達到穩定后,呈現每個單齒嚙合時產生的最大應力的周期變化規律。對比圖14的應力云圖結果分析,圖15中A類極大值為弧齒齒頂嚙入時齒頂中部邊緣呈現的周期性波峰應力值,D類極小值為弧齒齒頂嚙出時齒頂中部邊緣呈現的周期性波谷應力值,B類極大值為弧齒小端邊緣的波峰應力值,C類極大值為弧齒小端齒頂角邊緣的波峰應力值。圖16為弧齒齒面齒高方向系列結點的動態應力規律(節點序號從弧齒大端向小端,沿齒寬方向編號)。第1條曲線為弧齒齒根位置處的動態應力。當弧齒面嚙入時,齒根位置處的大端位置具有較大的動態應力,沿著齒寬方向動態應力逐漸減小,到齒寬中部后齒根應力變化較為穩定平緩。第4條曲線為弧齒齒高方向上中部位置的動態應力。弧齒大端位置具有較大的動態應力,沿著齒寬方向動態應力逐漸減小至一定數值而保持相對穩定。結果表明弧齒錐齒輪的負載扭矩主要由弧齒嚙合齒面的中部承載,第4條曲線的動態應力相對穩定,有利于弧齒錐齒輪的傳動平穩和疲勞壽命。第6條曲線為弧齒齒頂邊緣位置的動態應力。當弧齒嚙入或嚙出時,弧齒齒頂發生邊緣接觸的大端和小端都存在較大的動態應力。隨著弧齒齒面嚙入,負載扭矩主要由弧齒嚙合齒面的中部承載,此時弧齒齒頂邊緣接觸的中部也有較大的動態應力。

圖14 弧齒齒面的綜合應力云圖
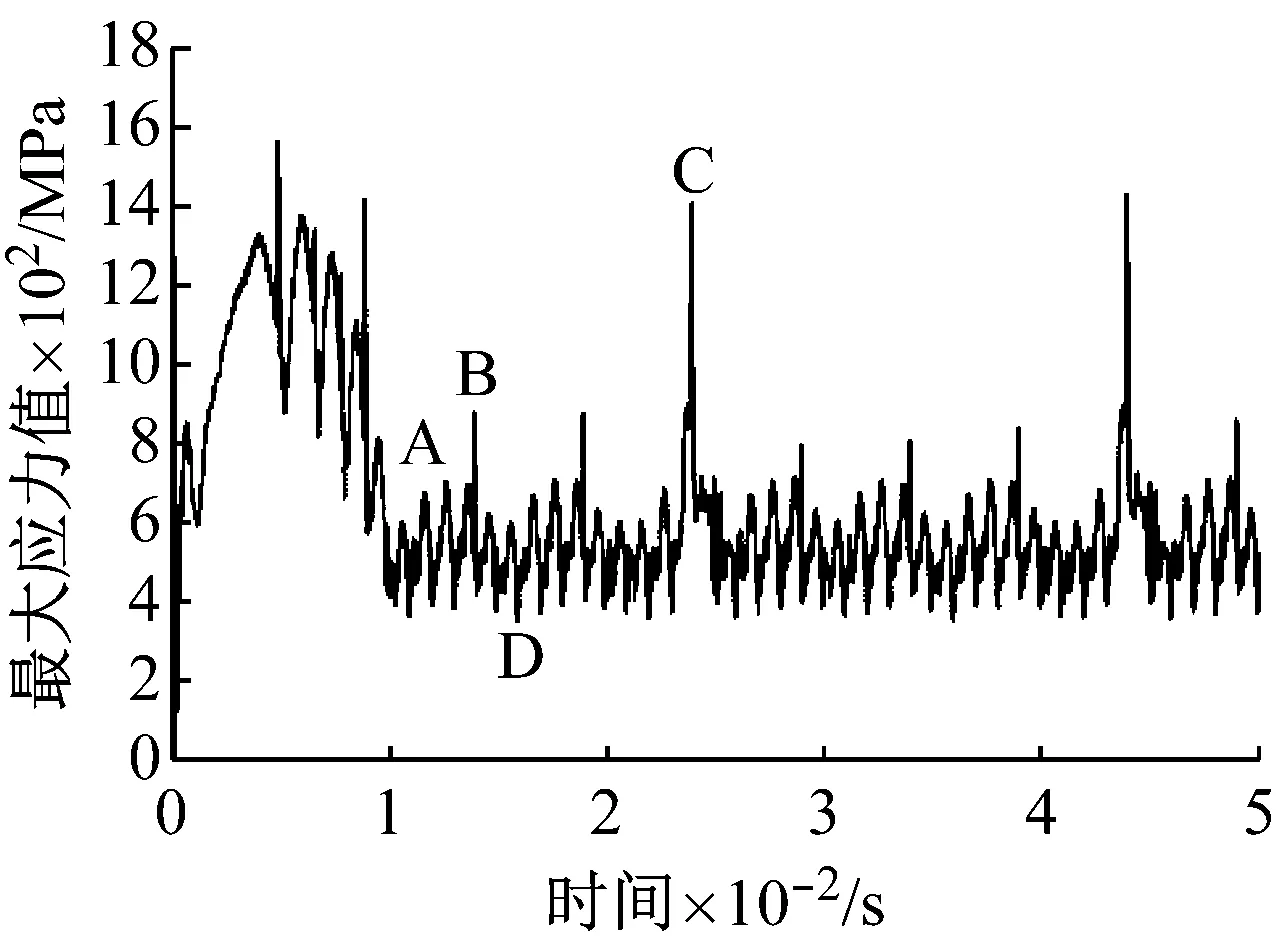
圖15 弧齒齒面的最大綜合應力
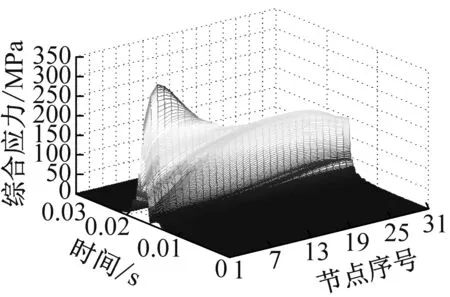
(a) 齒高方向的第1曲線
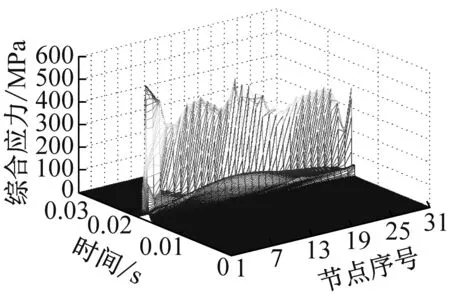
(b) 齒高方向的第4曲線
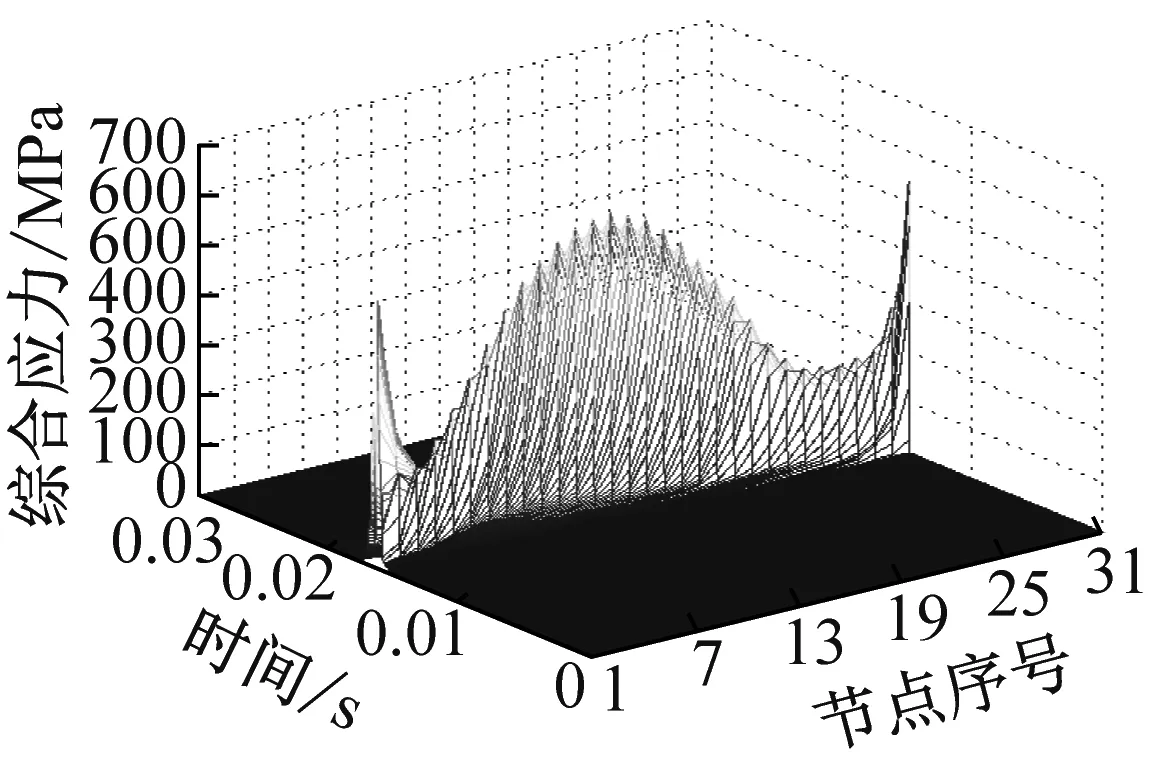
(c) 齒高方向的第6曲線
由于工況載荷和加工裝配誤差等外部因素,彈性變形和動態接觸等內部因素,弧齒錐齒輪在實際工況下通常會出現邊緣接觸現象。圖17為相鄰3對弧齒單齒嚙合時間內(Tz=0.001 s)齒面的最大應力規律。在弧齒錐齒輪傳動過程中,由于弧齒錐齒輪的彈性變形和動態接觸特性,相鄰弧齒在單齒嚙合時間內齒面不同位置發生動態接觸,存在不同的最大應力規律。給定參數對應的弧齒錐齒輪實例中,弧齒錐齒輪主要發生弧齒齒面中部和齒頂中部的承載接觸現象,而且在弧齒單齒嚙合時間內齒頂中部的邊緣接觸承載時間相對較長。齒頂中部和齒面小端中部有明顯的邊緣接觸現象,發生邊緣接觸時存在相對平穩變化的較大應力值。相鄰弧齒齒面中部承載接觸時最大應力的變化規律有所不同,當最大應力未從齒頂邊緣過度至齒面中部時存在一定的波動(圖17(a))。圖為18相鄰10對弧齒齒頂邊緣接觸時的最大應力。不同弧齒齒頂的邊緣接觸規律有所不同,但總體呈現出相鄰5對弧齒齒頂的周期性邊緣接觸規律。結果表明邊緣接觸改變了弧齒嚙合齒面的載荷分布規律,反映出弧齒齒輪的承載嚙合性能,更為真實地表現了弧齒齒輪動態接觸傳動的全過程。
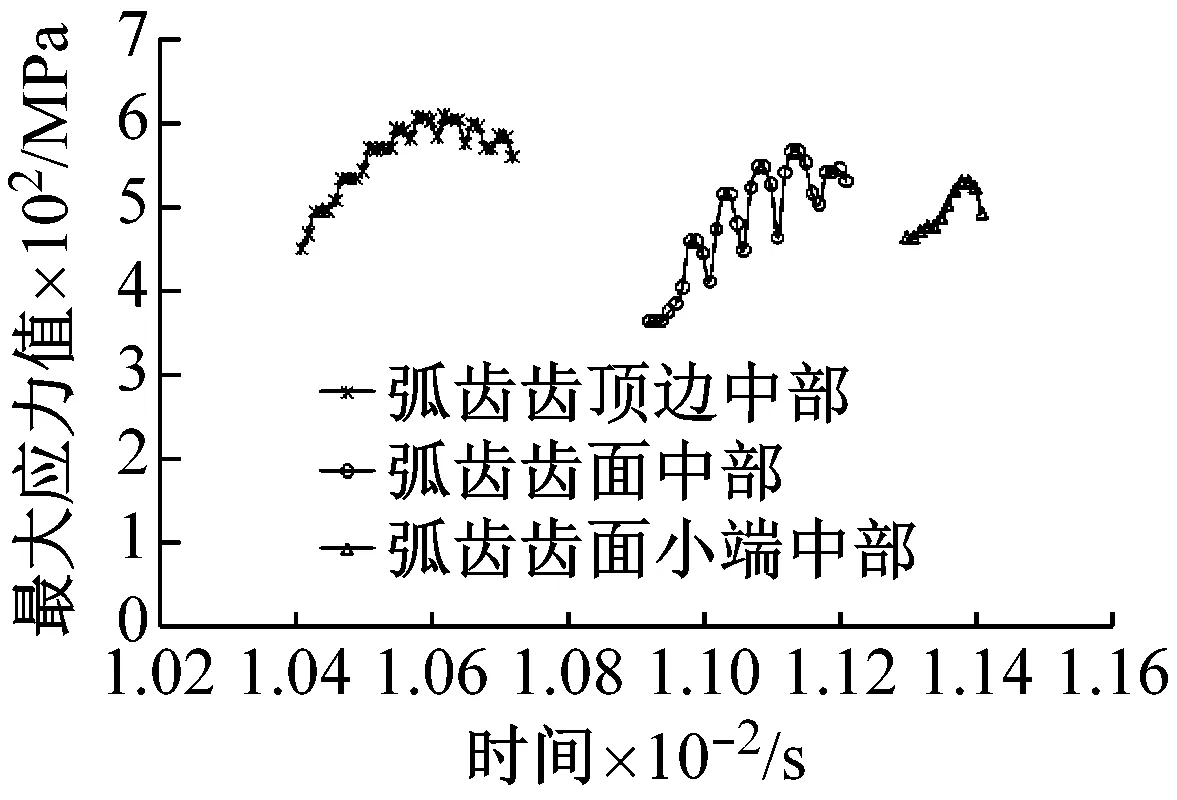
(a) 相鄰弧齒1的單齒嚙合時間內齒面最大應力
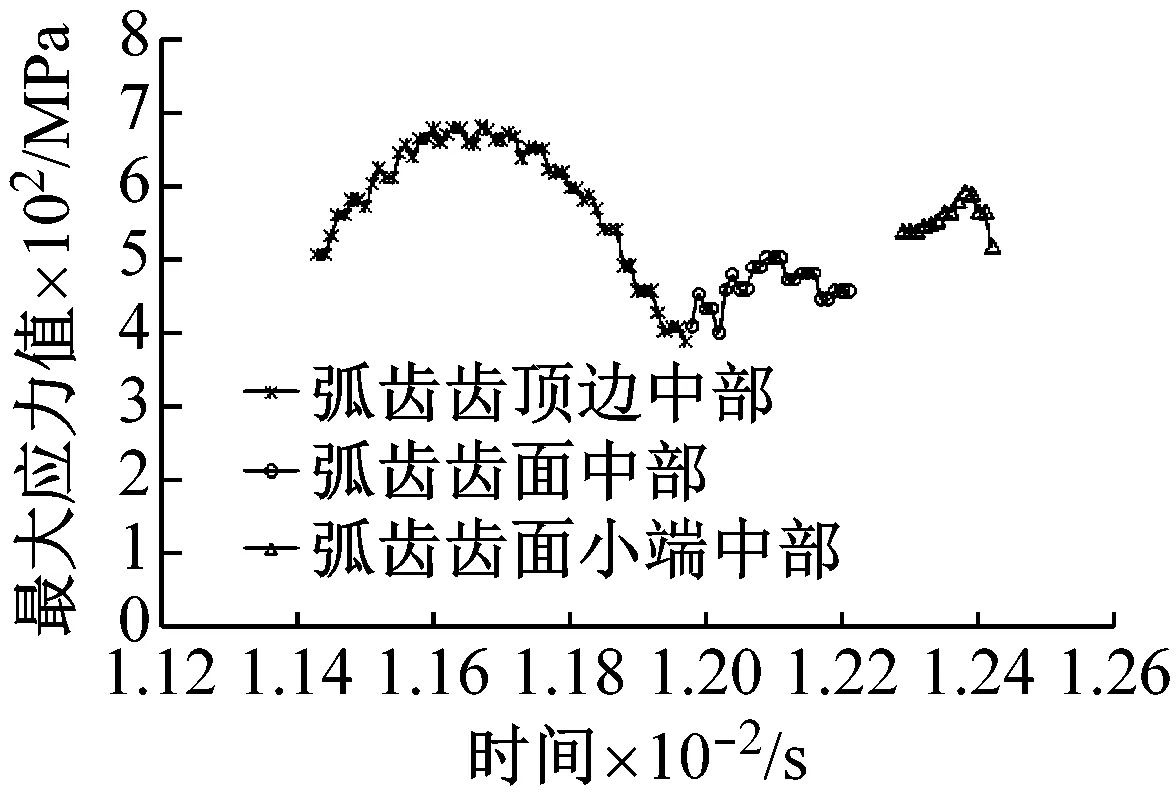
(b) 相鄰弧齒2的單齒嚙合時間內齒面最大應力
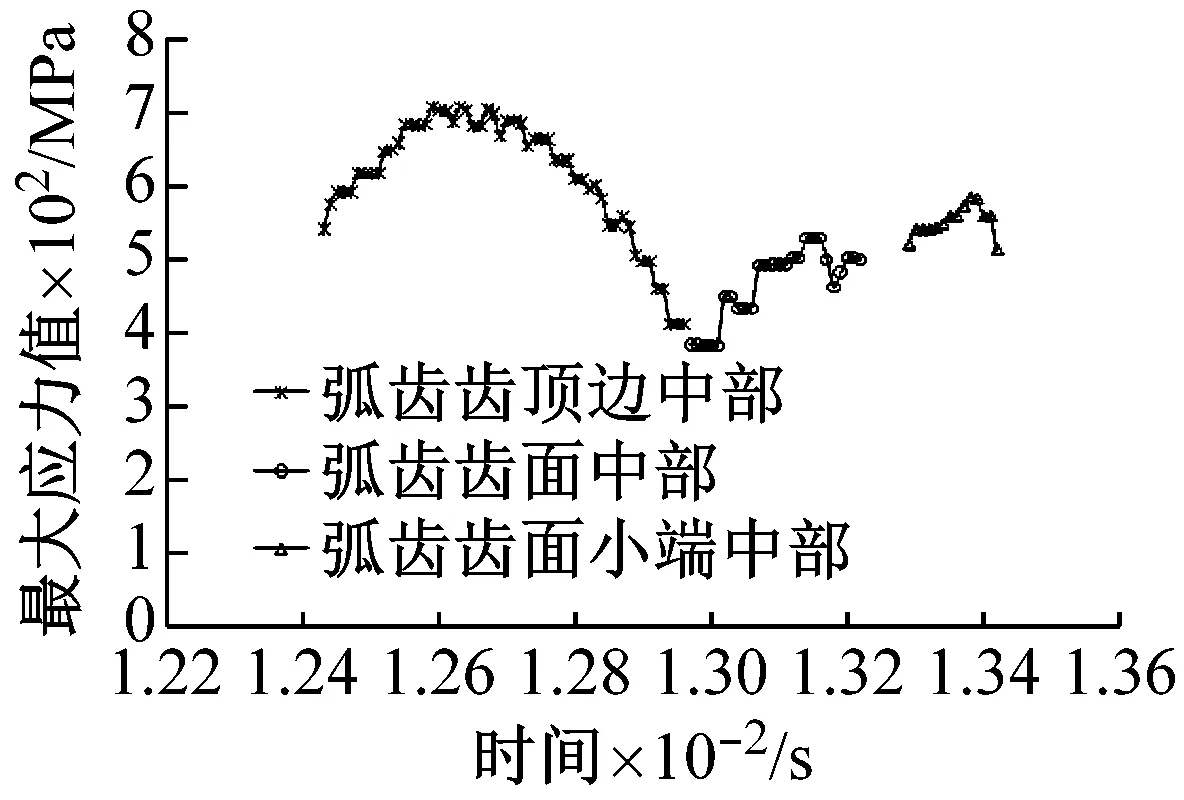
(c) 相鄰弧齒3的單齒嚙合時間內齒面最大應力
圖17 相鄰3對弧齒齒面的最大應力規律
Fig.17 Max Von Mises stress of adjacent three teeth
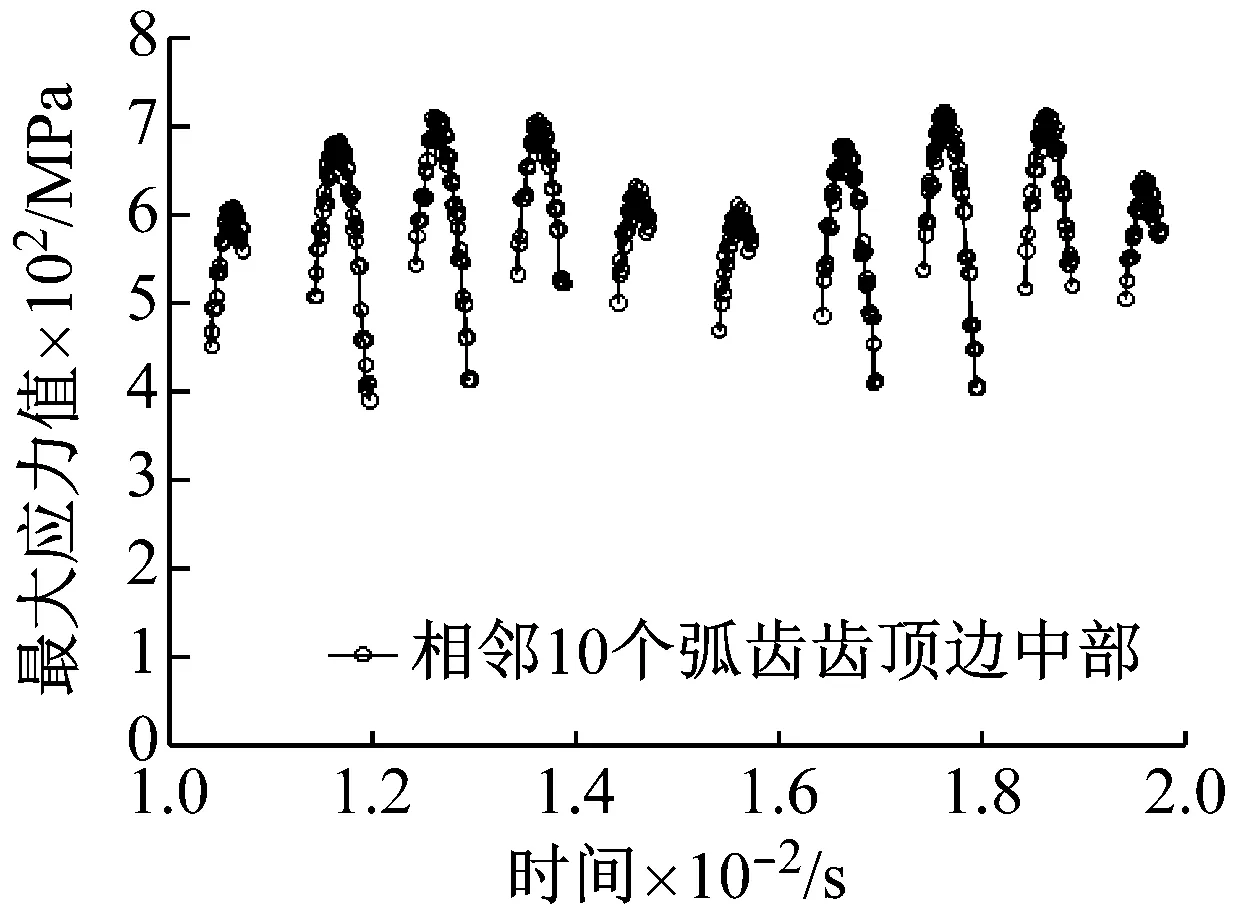
圖18 相鄰10對弧齒齒頂邊緣接觸時的最大應力
4 結 論
本文提出弧齒錐齒輪的多柔性體接觸動力學分析方法,分析了完整弧齒錐齒輪的彈性變形和精確弧齒齒面的三維動態接觸特性,對弧齒錐齒輪的動態嚙合傳動性能的影響規律,真實地模擬了弧齒錐齒輪的多柔性體、多界面動態接觸動力學特性,對高性能弧齒錐齒輪的動力學設計具有參考意義。
(1) 從動齒輪角速度是以嚙合頻率為基礎的小幅波動的周期變化規律,考慮彈性變形的柔性弧齒錐齒輪的角速度和轉角動態誤差較小,較為穩定。彈性變形對弧齒錐齒輪承載傳動性能有很大的影響,剛性弧齒錐齒輪方法會低估弧齒齒面的動態接觸力和齒輪系統的約束反力。
(2) 在啟動加速階段,弧齒錐齒輪的嚙合弧齒出現較大的應力值,穩定后呈現每個單齒嚙合時的最大應力的周期變化規律。弧齒大端的齒根應力值大于小端的,齒面中部承載應力分布較為穩定,齒頂大端、小端在嚙入嚙出時有較大的應力變化,齒頂中部承載應力分布較為平緩變化。
(3) 弧齒錐齒輪主要發生弧齒齒面中部和齒頂中部的承載接觸區域,齒頂中部發生邊緣接觸現象,承載時間相對較長,較大應力的平穩變化規律,總體呈現出相鄰5對弧齒齒頂的周期性邊緣接觸規律。

