層次分析法在企業(yè)權(quán)重管理中的應用研究

李 玲

(中鐵一局集團有限公司廣州分公司，廣東 廣州 511400)

在傳統(tǒng)的企業(yè)管理中，績效管理、業(yè)績考核中往往涉及考核指標的權(quán)重設置。目前企業(yè)對于考核指標的權(quán)重設計往往基于主要決策者的經(jīng)驗式管理得出，主觀性較大，制定過程也不夠透明，往往不能科學反映各指標的實際占比。由此制定的企業(yè)績效考核辦法有時在企業(yè)內(nèi)部有較多反對聲音，激勵效果明顯打折扣，在很多政府機關的績效考核中已被淘汰。因此，在企業(yè)管理工作中，應用新的工具和方法，探索可量化、可測量的權(quán)重制定辦法，提高權(quán)重因子制定的科學性，已成為提升企業(yè)管理水平和管理效率的必由之路。

層次分析法(Analytic Hierarchy Process，AHP) 是由美國的Thomas L. Saaty 教授于1987 年提出的一種科學分析方法。它與傳統(tǒng)的定性分析方法不同，更多的基于定性分析與定量分析耦合，可將以往的基于決策者經(jīng)驗的決策過程轉(zhuǎn)化為可量化、可測量的決策過程，進而實現(xiàn)企業(yè)決策水平的優(yōu)化和提升。

文章擬應用層次分析法，探索在企業(yè)權(quán)重管理中更科學的制定方法，使得權(quán)重制定的過程更透明、可測量，符合企業(yè)的發(fā)展和激勵機制的需要。

1 理論概述

層次分析法是將與決策過程相聯(lián)系的關聯(lián)因子分解成不同層次的子因子，并分析各層次的子因子的相關影響程度，根據(jù)各因子的影響程度不同，運用數(shù)學工具，進行定性分析和定量耦合分析的決策方法。

運用層次分析法解決問題的分析思路、決策過程與人類大腦對多維度問題的決策判斷過程極其相似。以購買手機為例: 假如有5 款手機型號A、B、C、D、E 供選擇，購買者會根據(jù)諸如品牌、操作系統(tǒng)、手機性能、攝像效果、內(nèi)存大小和價格等一些考慮因素或因子去比選這5 款候選手機。首先會考慮這些影響因素或因子在心中的占比。比如追求品牌、不在乎價格，當然會首先考慮品牌，而注重性價比或僅需要基本功能的人則會重點考慮價格因素; 如果是一個攝影愛好者，則多會注重手機的攝像效果等。然后，就每一個比選條件將5 款手機進行對比選擇，譬如C 品牌最好，D 次之; B 攝像效果最好，E 次之; D 性價比最高等。最后將每個層次的比較判斷進行綜合，在A ～E 手機中確定哪個作為最佳購買手機候選。

2 模型描述

層次分析法可以視為一個影響因子的分層模型。我們需要決策的結(jié)果，比如企業(yè)的績效指標制定放置在最上層; 對于為實現(xiàn)這個績效目標而細化的各個指標放置在中間層; 如果需要決策的過程目標過于復雜，比如企業(yè)內(nèi)部存在分類績效指標，則可將中間層的指標進一步細化，放置在最下層。利用層次分析法決策問題需要把各種需要考慮的因素放在適當?shù)膶哟蝺?nèi)，并用層次結(jié)構(gòu)圖清晰地表達這些因素的關系。

3 分析步驟

(1) 建立層次結(jié)構(gòu)模型。在分析具體需要解決問題的基礎上，將有關的各個因素按照不同屬性自上而下地分解成若干層次。最頂層為目標層，一般只有1 個因素，最底層通常為方案層，中間可以有多個或一個層次，通常為指標層。當指標超過9 個時，應進一步分解出子指標層。

(2) 基于調(diào)查樣本建立對比矩陣。利用層次分析法定義的比較尺度，按照由上至下的原則，相互對比指標之間的重要程度(以1～9 表示) ，建立矩陣表格，將基于調(diào)查樣本的統(tǒng)計結(jié)果填充到矩陣表格中，形成基于調(diào)查樣本統(tǒng)計結(jié)果的對比矩陣。

(3) 計算對比矩陣的特征向量，進而計算出的最終指標權(quán)重，并通過計算一致性比率進行權(quán)重一致性的有效性檢驗。

4 層次分析法在企業(yè)權(quán)重管理中的應用

4.1 確定指標

根據(jù)企業(yè)的業(yè)務活動和工作流程，擬定需要確定權(quán)重的評價指標清單。如羅列需要確定權(quán)重的評價指標: 生產(chǎn)計劃、上繳款、合同管理、科技創(chuàng)新、獲獎、事故等。

(1) 統(tǒng)計評價指標重要性

將需要確定權(quán)重的評價指標，排列在比較表中，如表1，請公司內(nèi)部員工就其重要性進行兩兩比較選擇。

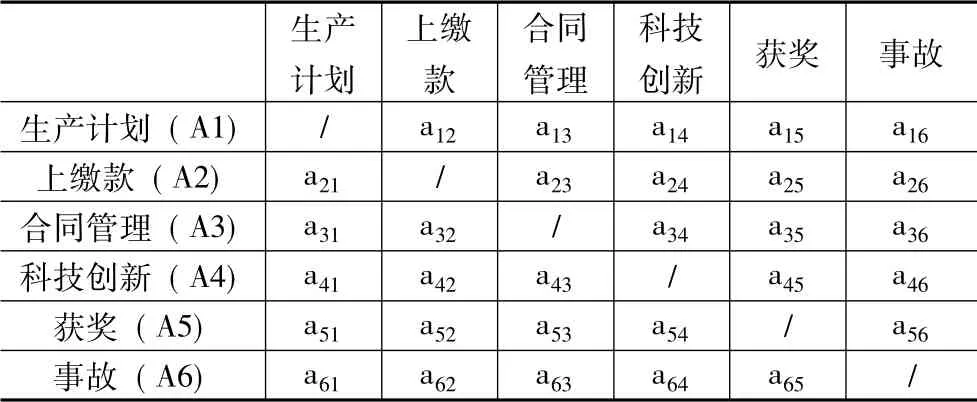
表1 評測指標比較表

例如，a21處代表2 行處的指標對比1 列處的指標的重要性，即上繳款對于生產(chǎn)計劃的重要程度; a65處代表6 行處的指標對比5 列處的指標的重要性，即事故對于獲獎的重要程度，依此類推。a21與a12、a65與a56應為倒數(shù)關系。

重要性用標度表示，如: 1 表示兩個具有同樣重要性(或相同強) ，3 表示一元素比另一元素稍微重要(或稍微強) ，5 表示一元素比另一元素比較重要(或比較強) ，7 表示一元素比另一元素明顯重要(或明顯強) ，9 表示一元素比另一元素絕對重要(或絕對強) ，2、4、6、8 則表示在上述兩個標準之間折中時的標度。

(2) 構(gòu)造雙對比矩陣

對公司員工對于指標重要性的調(diào)查采用平均法進行匯總，計算出統(tǒng)計結(jié)果，形成雙對比矩陣，如表2 所示。

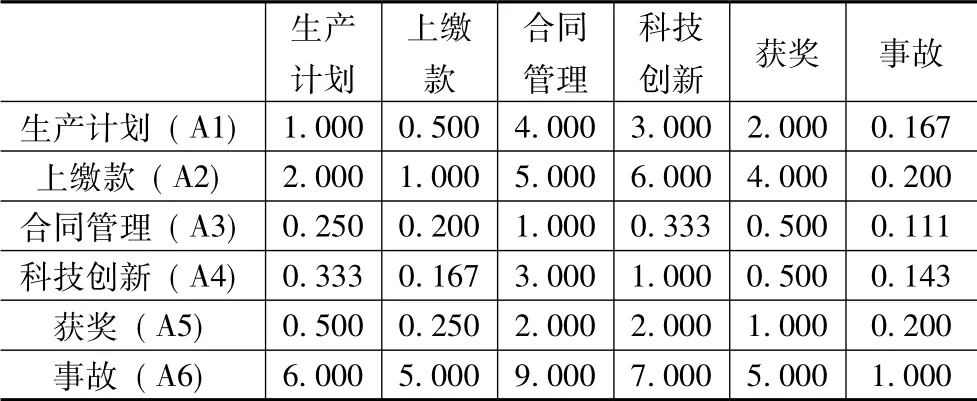
表2 評測指標比較統(tǒng)計表

(3) 計算矩陣的特征向量和指標權(quán)重

對雙對比矩陣，利用下面的公式1 進行歸一化計算。

式中，bij就是用各列的元素除以列的和。

得到的結(jié)果為一個新的矩陣，我們暫命名為B 矩陣，

如表3。

表3 矩陣B

對矩陣B 每一行進行求和，計算出特征向量B，可知

B1=0.737，B2=1.275，B3=0.211，B4=0.350，B5=0.458，B6=2.969

上述求出的特征向量，用下面的公式2 進行歸一化計算，即可得到各指標的最終權(quán)重值。

由公式可計算出各指標的權(quán)重值。

W1=0.123，W2=0.213，W3=0.035，W4=0.058，W5=0.076，W6=0.495

4.2 矩陣一致性檢驗

我們需要對企業(yè)績效指標相互對比，如果存在: A＞C，C＞B，則必得出A＞B，否則就是建立的雙對比矩陣存在不一致。舉例來說，如果B 對于C 的重要值為2，C 對于A 的重要值也為2，那么B 對于A 的重要值應該為4，但是如果最終不是4，是5 或者9，代表對比矩陣的一致性存在一定問題。所以需要檢驗對比矩陣的一致性，確保兩兩比較的時候，不會出現(xiàn)以上的錯誤。

在檢驗對比矩陣的一致性時，首先需要計算對比矩陣的最大特征根，然后計算對比矩陣的一致性指標CI，再計算平均隨機一致性指標RI。如果RI＞0.1，就表示計算出的指標權(quán)重未保持顯著水平，對比矩陣進行調(diào)整。如果RI＜0.1，即表示計算出的指標權(quán)重保持顯著水平，對比矩陣的一致性通過檢驗，權(quán)重計算結(jié)果有效。

5 結(jié) 論

通過層次分析法(AHP) 進行企業(yè)內(nèi)部指標的權(quán)重設計，可以由眾多員工進行投票評選各指標的重要性，建立對比矩陣，使得指標制定來源于科學的原始數(shù)據(jù)，間接體現(xiàn)了基層員工的總體意愿，避免了以往權(quán)重設計由主要決策者經(jīng)驗式?jīng)Q策的弊端，能有效提升決策權(quán)威，顯著增強獎懲政策的執(zhí)行力。同時，通過計算出的權(quán)重結(jié)果進行一致性檢驗，可以檢驗原始統(tǒng)計數(shù)量是否有矛盾，是否與對比矩陣中每組指標之間的對比標度保證一致，保證權(quán)重計算的準確性與一致性，也使得權(quán)重制定的過程更透明、更量化，符合企業(yè)的發(fā)展和激勵機制的需要。

任何決策工具都不是完美的。層次分析法對于指標權(quán)重的計算主要依賴于樣本統(tǒng)計結(jié)果，故企業(yè)在實際應用過程中，需要通過增加培訓、細化調(diào)查等方式，保證調(diào)查樣本的重要性與對比結(jié)果的一致性，才能保證層次分析法的準確度。