后燃燒效應對約束空間內爆炸載荷的影響規律

徐維錚 ，吳衛國

1武漢理工大學高性能艦船技術教育部重點實驗室，湖北武漢430063

2武漢理工大學交通學院，湖北武漢430063

0 引言

針對約束空間內的爆炸問題，爆炸后燃燒效應是需要重點關注的內爆炸物理現象。大多數炸藥（TNT炸藥、溫壓炸藥、SDF混合型炸藥［1］等）的爆轟產物具有負氧性，高溫高壓爆轟產物在膨脹過程中會與周圍空氣中的氧氣進行劇烈的燃燒反應并釋放大量能量，這一物理現象為后燃燒效應［2］。后燃燒效應對爆炸沖擊波的傳播過程、沖擊波壁面反射壓力、準靜態壓力都會產生一定的影響。

為了研究約束空間內后燃燒效應對爆炸載荷的影響規律，國內外學者開展了大量的實驗和數值模擬研究。金朋剛等［3］采用壓力傳感器測量了在密閉罐體內分別存在氮氣、空氣和氧氣3種條件下TNT炸藥在后燃燒過程中產生的準靜態壓力，結果表明，在氧氣環境下，TNT炸藥的后燃燒效應較明顯，能夠產生更大的準靜態壓力。李鴻賓等［4］在容積為500 L的密閉爆炸罐中進行了TNT炸藥爆炸實驗，發現隨著環境中氧氣量的增大，準靜態壓力增大，說明提高環境中的氧氣含量能夠提高爆轟產物的反應率。李芝絨等［5］通過實驗測量了在圓柱形密閉爆炸罐內分別存在空氣和氮氣這2種條件下溫壓炸藥爆炸的沖擊波峰值以及罐體內的準靜態壓力，結果表明，在爆轟反應階段，氧氣與超細鋁粉發生氧化反應，空氣環境中的沖擊波峰值和沖量比氮氣環境的略高；在后燃燒階段，氧氣與鋁粉混合產生后燃燒反應，釋放出大量的熱量，與氮氣環境相比，空氣環境中的準靜態壓力和熱響應溫度峰值顯著增大。Kuhl等［6］提出采用多流體模型描述考慮后燃燒效應的爆炸場，將爆炸組分劃分為燃料、空氣和產物3種成分，分別對這3種成分建立質量、動量、能量守恒方程，在爆炸過程中，采用狄拉克函數進行燃燒陣面的捕捉，釋放后燃燒能量，并開發了網格自適應數值計算程序。Togashi等［7-8］將自主開發的三維爆炸波數值計算程序與勞倫斯利弗莫爾實驗室開發的Cheetah編碼銜接，利用Cheetah編碼計算后燃燒能量，再將后燃燒能量添加到自主開發的程序，實現爆炸過程中后燃燒效應的模擬。

爆炸流場包含高密度比和高壓力比強間斷等復雜流場結構，對爆炸過程進行數值模擬時，需要高精度、強穩定性激波捕捉格式。Liu等［9］提出了加權本質無振蕩格式（Weighted Essentially Non-Oscillation Scheme，WENO），Jiang等［10-11］發展了該格式并擴展了其應用。目前，WENO格式作為一種典型的高精度激波捕捉格式，對流場內的激波間斷具有較高的分辨率，適用于求解包含激波、膨脹波以及接觸間斷等復雜結構的流場。

由于后燃燒過程涉及復雜的多組分燃燒化學反應，如果考慮詳細的化學反應過程，不僅程序編寫復雜，且由于化學反應時間尺度與流場時間尺度存在差別，計算量大，難以應用于實際工程問題計算中。為此，本文擬提出一種考慮后燃燒效應的簡化反應率模型，考慮到WENO格式精度高及穩定性較好的優勢，基于Fortran平臺，采用五階WENO有限差分格式，自主開發約束空間內考慮爆炸后燃燒效應的二維數值計算程序，并探討反應速率及后燃燒能量大小對約束空間內爆炸載荷的影響規律。

1 控制方程及數值求解

為了近似考慮爆炸后燃燒效應，在Miller反應率模型［12］思想的啟發下，提出一種考慮炸藥爆炸后燃燒效應的數值計算方法，初步探討后燃燒效應對約束空間內爆炸載荷的影響規律。

Miller反應率模型最初提出的目的是近似描述含鋁炸藥爆轟過程中鋁粒子在爆轟波陣面后的反應過程［12］。我們嘗試將模型思想推廣應用到約束空間內爆炸后燃燒效應的數值計算中。本文采用的反應率模型如下：

式中：a為反應速率常數；p為流體壓力；α為后燃燒過程中反應率（初始時α=1，反應完成后α=0）。

不考慮后燃燒效應的可壓縮歐拉方程為

其中，

將反應率模型式（1）耦合到式（2）中，并以源項的形式進行后燃燒能量的添加，可得考慮后燃燒效應的可壓縮歐拉方程為

其中，

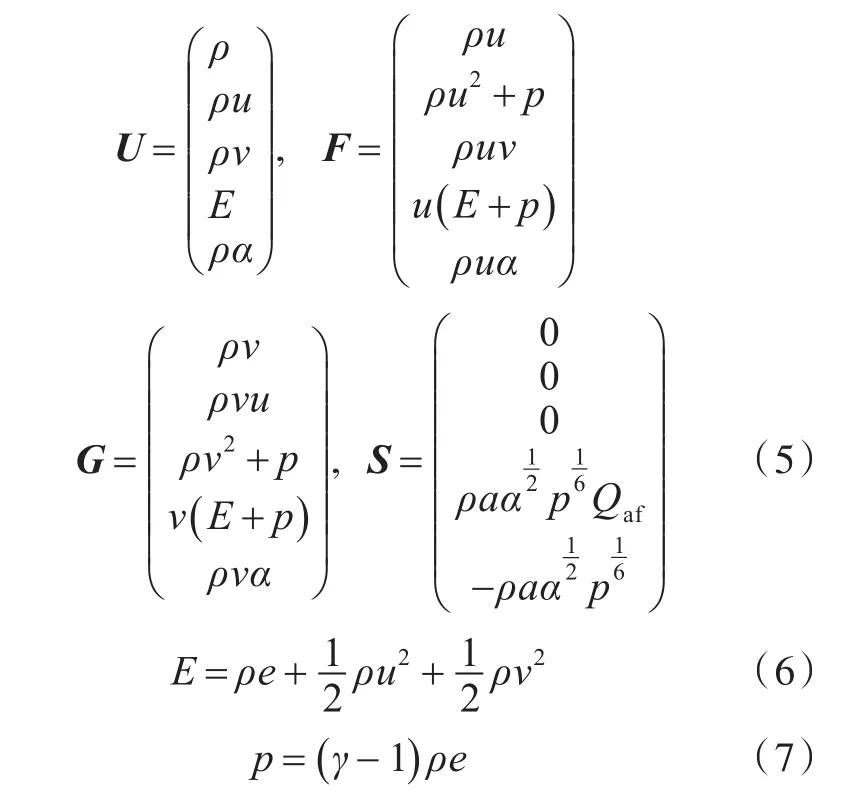
以上式中：ρ為密度；u，v分別為x，y方向上的速度分量；E為單位體積流體的總能量；e為比內能；Qaf為爆炸后燃燒過程中單位質量釋放的能量，J/kg；γ為氣體的絕熱指數，文中γ統一取為1.4。

式（5）在每個方向上均可以看成是一個帶有源項的雙曲守恒律方程：

例如，針對x方向，式（8）的半離散守恒型格式為

2 約束空間內爆炸后燃燒效應數值計算

采用五階WENO有限差分格式，自主開發了約束空間內考慮爆炸后燃燒效應的二維數值計算程序。自主程序對于爆炸波的數值計算可靠性在文獻［14-15］中已經得到驗證。本節采用自主程序對約束空間內炸藥爆炸過程進行數值模擬研究，主要探討反應率演化過程及后燃燒能量的加入對爆炸載荷的影響規律。

2.1 艙室尺寸及測點布置

長方形艙室的尺寸如圖1（a）所示，圖中數值單位為mm。在艙室壁面上設置了3個典型測點，用于監測爆炸載荷時間歷程和反應率時間歷程。均勻網格步長取為10 mm，如圖1（b）所示。

圖1 艙室尺寸及網格劃分Fig.1 Size of cabin and mesh partition

2.2 初始條件和邊界條件

基于瞬時爆轟假定，將方形炸藥等效為均勻高壓氣團，具體參數為：邊長22.2 mm，密度1 630 kg/m3，壓力 3.057 9×109Pa。炸藥設置在艙室中間，即圖2（a）中的紅色區域，周圍藍色區域為空氣域，空氣密度為1.0 kg/m3，壓力為1.0×105Pa。初始時刻反應率分布見圖2（b）中的紅色區域。初始時刻反應還沒發生，炸藥所在區域反應率為1，艙室其他區域反應率為0。壁面邊界條件設置為剛性邊界，由于沖擊波與結構變形耦合效應十分復雜，這里暫時不考慮艙室結構的變形。

2.3 計算工況

圖2 爆炸初始條件Fig.2 Initial condition for the explosion

為了探討反應速率和后燃燒能量大小對爆炸過程的影響規律，選取2類典型工況進行計算。工況1：后燃燒單位質量釋放的能量Qaf=4.69×106J/kg，保持其他參數不變，反應速率常數分別取為a=0，10，40。工況2：反應速率常數為a=10，保持其他參數不變，后燃燒單位質量釋放的能量分別取為Qaf=0，3.0×106，4.69×106J/kg。

2.4 反應率演化過程分析

為了探討爆炸后反應率在艙室內部的演化過程，給出了2種工況在不同時刻的反應率分布圖，如圖3所示，其中左圖為a=0，Qaf=4.69×106J/kg；右圖為a=10，Qaf=4.69×106J/kg。由圖3可知，2種工況下，反應率在不同時刻總體呈現相似的空間分布形態。在爆炸工況a=0，Qaf=4.69×106J/kg中反應速率常數為零，即在整個爆炸過程中沒有發生反應，沒有后燃燒能量的加入。根據式（4）可知，該工況求解的是爆轟產物質量分數的演化過程；由于爆炸工況a=10，Qaf=4.69×106J/kg中反應速率常數不為零，反應速度快，從而導致艙室內部的反應率快速下降，最終趨近于0。

圖3 不同時刻的反應率分布圖（左：a=0，Qaf=4.69×106J/kg；右：a=10，Qaf=4.69×106J/kg）Fig.3 Reaction rate distribution at different moments（left：a=0，Qaf=4.69× 106J/kg；right：a=10，Qaf=4.69 × 106J/kg）

為定量顯示艙室內部反應率的變化，圖4給出了工況1（a=0，10，40；Qaf=4.69×106J/kg）壁面測點1和2的反應率時間歷程曲線。由圖4可見，隨著反應速率常數a的增大，反應率迅速下降，反應完成后，反應率等于0。這里需要說明的是，當反應速率常數a=0時，反應沒有發生，根據式（4）可知，反應率的演化過程就是爆轟產物質量分數的演化過程，由于爆炸后爆轟產物與艙室內部的空氣進行了復雜的摻混過程，因此艙室內部爆轟產物的質量分數數值將趨近于大于0而小于1。

圖4 工況1壁面測點1和2的反應率時間歷程曲線Fig.4 Time history curves of reaction rate for gauging points No.1 and No.2 in explosion case one

圖5給出了工況2（Qaf=0，3.0×106，4.69×106J/kg；a=10）壁面測點1和2的反應率時間歷程曲線。由圖5可以看出，在反應速率常數一定的情況下，后燃燒能量的加入對反應速率時間歷程的影響顯著，然而隨著后燃燒能量Qaf的增大，其大小對反應速率時間歷程的影響較小。

圖5 工況2壁面測點1和2的反應率時間歷程曲線Fig.5 Time history curves of reaction rate for gauging points No.1 and No.2 in explosion case two

2.5 后燃燒能量的加入對爆炸載荷的影響

為了探討不同反應速率常數a對艙室內部爆炸載荷的影響規律，給出了工況1（a=0，10，40;Qaf=4.69×106J/kg）壁面典型測點3的超壓時間歷程曲線（圖6）。由圖6可以看出，后燃燒能量的加入明顯增強了沖擊波載荷和沖量；隨著反應速率常數a的增大，沖擊波到達時間提前，沖擊波峰值增大，沖量增大。由于后燃燒能量的加入，與工況a=0，Qaf=4.69×106J/kg相比，工況a=10，40；Qaf=4.69×106J/kg的準靜態超壓峰值增大。由于后燃燒能量相同，工況a=10，Qaf=4.69×106J/kg和工況a=40，Qaf=4.69×106J/kg具有相同的準靜態超壓峰值。

圖6 不同反應速率常數下測點3爆炸載荷的時間歷程曲線Fig.6 Blast load time histories with different reaction rate constants for gauging point No.3

為了探討不同后燃燒能量大小Qaf對艙室內部爆炸載荷的影響規律，給出了工況2（Qaf=0，3.0×106，4.69×106；a=10）壁面典型測點 3的超壓時間歷程曲線（圖7）。由圖7可以明顯看出，在反應速率常數一定的情況下，隨著后燃燒能量Qaf的增大，載荷強度增大，最終的準靜態超壓峰值增大。

為了初步驗證本文后燃燒能量加入的可靠性，從準靜態超壓峰值的角度進行了對比分析。根據文獻［16］可知，封閉艙室內部準靜態超壓峰值的計算公式為

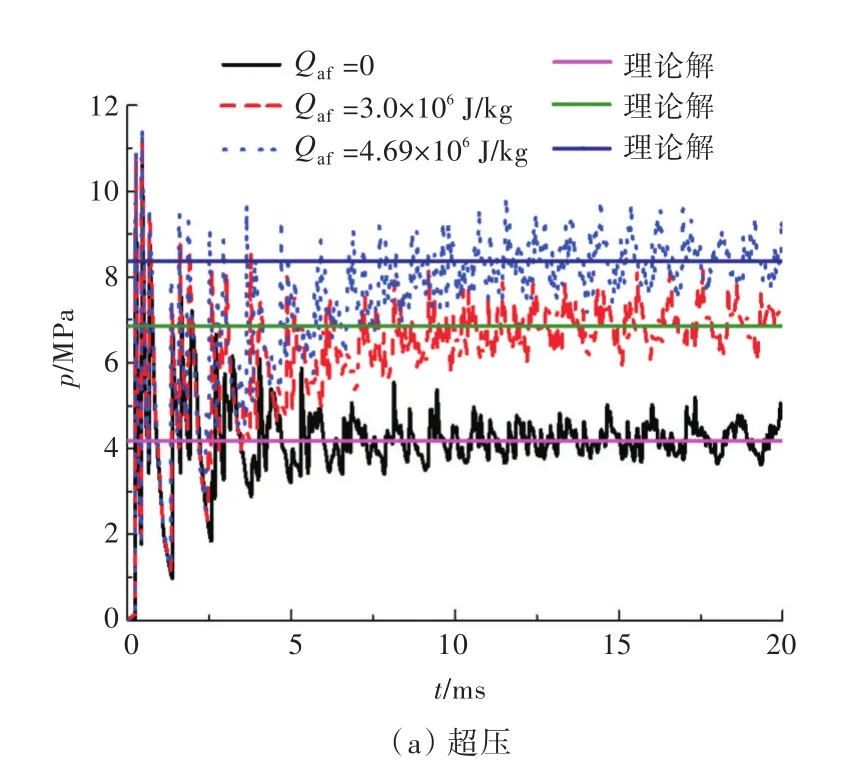
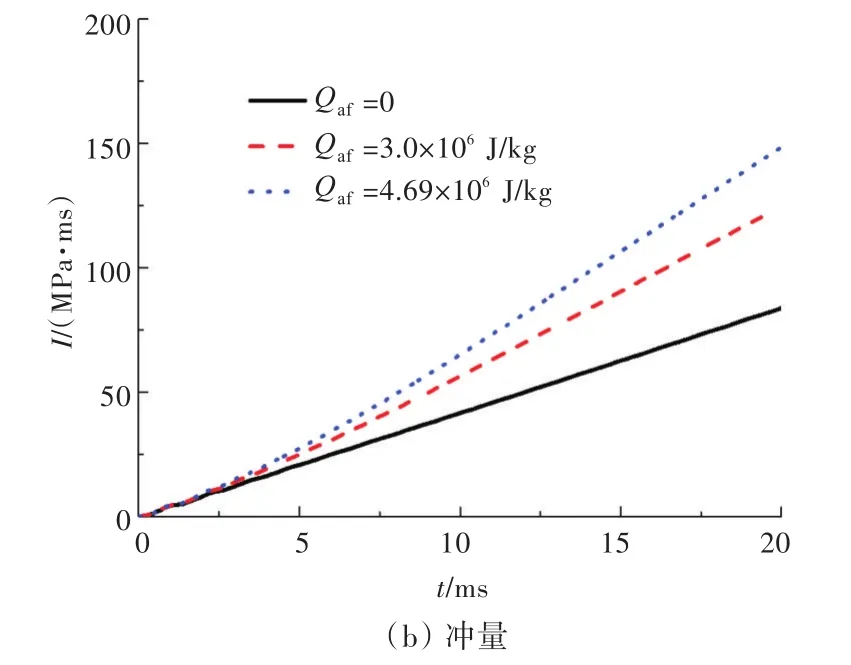
圖7 不同后燃燒能量下測點3的爆炸載荷時間歷程曲線Fig.7 Blast load time histories with different afterburning energy for gauging point No.3

式中：m為炸藥質量；Qtol=QTNT+Qaf，為爆炸過程中釋放的總能量，包含后燃燒過程中釋放的能量Qaf，其中QTNT=4.69×106J/kg，為炸藥的爆熱；p0為初始大氣壓力；V為艙室體積；ρE=1 630 kg/m3，為炸藥密度。

將工況1，2中的后燃燒能量Qaf代入式（10），得到準靜態超壓峰值的理論計算值，再將理論計算結果與數值模擬結果進行對比，結果如圖6（a）和圖7（a）所示。由圖可以明顯看出，理論計算結果與數值模擬結果吻合較好，證明了后燃燒能量加入的可靠性。

3 結 論

通過研究得到如下主要結論：

1）在后燃燒能量大小一定的情況下，反應速率常數增大時，沖擊波到達時間提前，沖擊波峰值、沖量均增大，準靜態超壓峰值保持不變。

2）在反應速率常數一定的情況下，隨著后燃燒能量的增大，沖擊波峰值、沖量及準靜態超壓峰值均增大，后燃燒能量的加入能顯著增強爆炸載荷強度。

3）本文針對爆炸后燃燒過程的數值計算，盡管沒有考慮復雜的多組分反應過程，然而采用一種簡化的反應率模型近似描述后燃燒能量對爆炸載荷的影響，不失為一種滿足實際工程計算的有效方法。

本文的研究方法及結果可為進一步研究內爆炸復雜多組分后燃燒效應及抗爆結構設計提供參考和借鑒。