滑行艇阻力計算方法對比研究

孫源，盧曉平，李井煜，王中

海軍工程大學艦船與海洋學院，湖北武漢430033

0 引 言

滑行艇，是指在高速下全艇的重量大部分由水動升力支持的船艇，亦即實現了動力航行的船艇，其優良的高速特性使之得到了廣泛的關注和應用。基于該型艇特殊的性能和速度要求，高速滑行艇的設計及性能分析過程十分重要，因而建立快速、準確的滑行艇阻力計算方法具有重要意義。經過數十年的研究和發展，滑行艇阻力計算研究取得了許多有意義的成果，同時也還存在著不少尚需解決的問題。現有的滑行艇阻力計算方法可分為2大類：半經驗半理論方法和數值計算方法。其中，半經驗半理論方法主要包括［1］：

1）利用現有艇的統計資料進行估算；

2）查潔法［2-3］。繼前蘇聯中央流體動力中心之后，我國艦船設計單位也開始使用該方法對滑行艇阻力進行計算；

3）SIT法［4］。該方法是根據美國Stevens實驗室水池試驗結果而提出，普遍應用于歐美等國；

4）舒福德—勃朗法。該方法由 Shuford［5］根據“橫流理論”提出，然后，Brown［6］通過大量實驗對其原始公式進行了改進。

數值計算方法作為一種新興而有效的工具，已經可以對排水型船舶阻力進行較為準確的預報。但在滑行艇阻力預報方面，國內外有關CFD水動力計算及其工程運用的相關研究仍然較少。Yousefi等［7］針對近年來在高速滑行艇水動力方面的研究進行了總結，并對比了多種商用CFD軟件的主要特點。曹洪建［8］使用FLUENT軟件，對滑行艇于靜水中的直航運動進行了數值模擬，證明采用該軟件計算滑行艇阻力性能具有一定的準確性。魏子凡等［9］基于NUMECA系列軟件，對多種滑行艇進行了數值計算及阻力分析，并以此為依據對滑行艇附屬裝置進行了優化。常亮等［10］采用運動域方法對滑行艇流場進行了數值模擬，經試驗驗證，表明該方法具有較好的準確性。孫華偉等［11］運用STAR CCM+軟件探討了結構網格因素對滑行艇阻力計算精度的影響。王碩等［12］同樣基于STAR CCM+軟件，采用切割六面體網格對滑行楔形體和滑行艇進行了阻力預報，所得結果的精度能夠滿足工程應用要求。

本文將分別使用半理論半經驗方法以及基于STAR CCM+軟件的數值計算方法對滑行艇模型阻力開展計算，并采用試驗所得數據進行對比和驗證，證明半理論半經驗方法及CFD數值計算方法在解決滑行艇滑行狀態下的阻力計算方面具有可靠性，用以為后續多體滑行艇阻力計算打下基礎。

1 艇型參數及計算方法

1.1 艇型建立

本文所研究的滑行艇艇型是在確定主尺度的前提下，依據美國62系列滑行艇的船型資料確定船型函數，然后再結合仿射變換法和船型函數變換法得到具體的艇型。其橫剖線圖及三維構型圖如圖1所示，根據該艇型制作的1/10比例模型參數如表1所示。

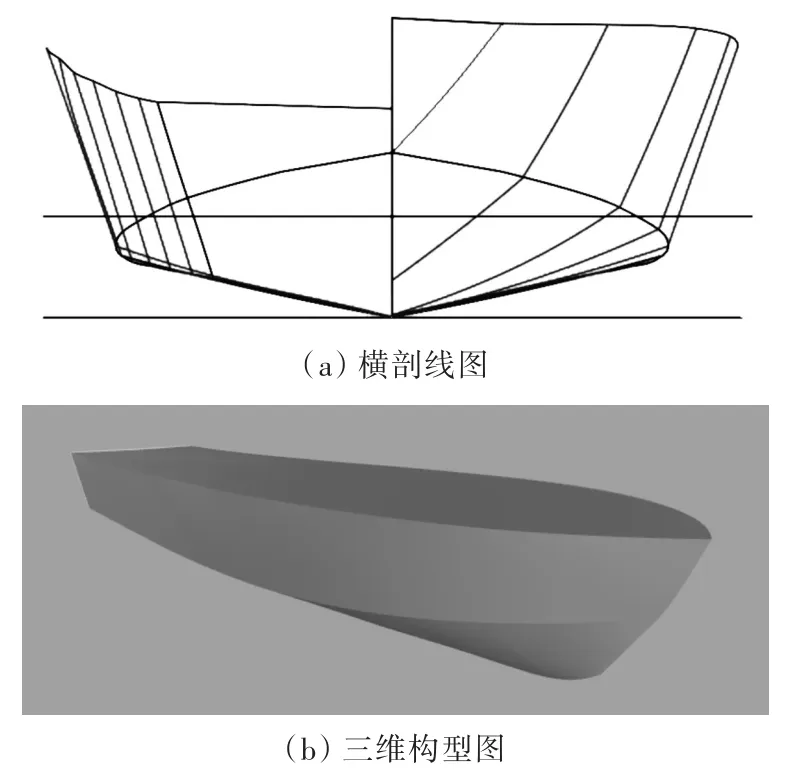
圖1 滑行艇線型圖Fig.1 Profile of the planing craft

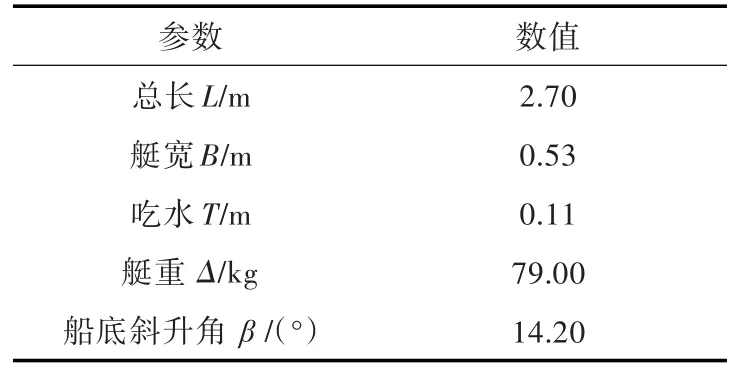
表1 模型參數Table 1 Model parameters

1.2 半理論半經驗方法

常用的半理論半經驗方法包括查潔法、SIT法和舒福德—勃朗法等，這類方法均是以基本的理論公式為基礎，再結合大量的試驗數據進行經驗系數的修正，從而得到既能反映物理實質，又能針對因物理模型過分簡化而引起的誤差進行補償的一類計算方法。這些方法被廣泛應用于各國滑行艇的阻力計算之中。其中，查潔法已在我國船舶設計單位中得到使用；SIT法作為姆雷法的修正及補充，也多見于滑行艇阻力計算研究中；而舒福德—勃朗法從原理上講較前兩種方法更為合理，但由于其計算較為復雜，并未得到廣泛應用。

1.2.1 查潔法

采用查潔法計算滑行艇阻力的具體步驟如下：

1）已知艇重Δ，航速V，艇寬B（舯部折角線寬度和艉部折角線寬度的平均值），重心至艉板的水平距離ξg，計算艇寬傅汝德數，升力系數（其中ρ為流體密度），重心縱向位置系數mΔ=ξg/B。

2）求解方程組（1），得到縱傾角α和浸濕長寬比λ。

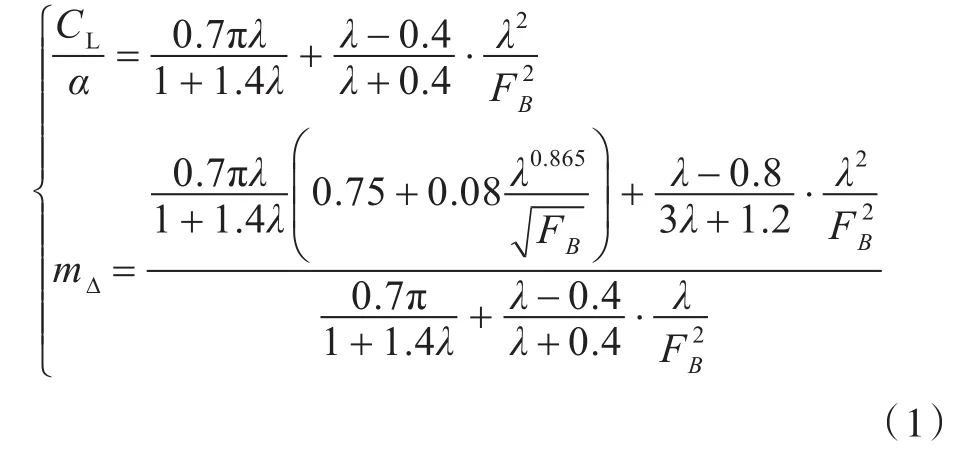
3）對縱傾角α進行計及斜升角β影響的修正。

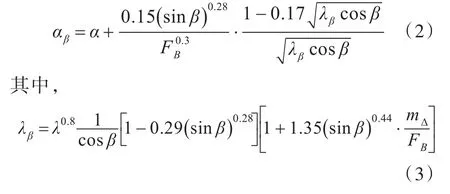
4）計算浸濕面積S=λB2、浸濕長度I=λB以及雷諾數Rn=V·I/ν，其中ν為運動粘性系數。5）計算總阻力：

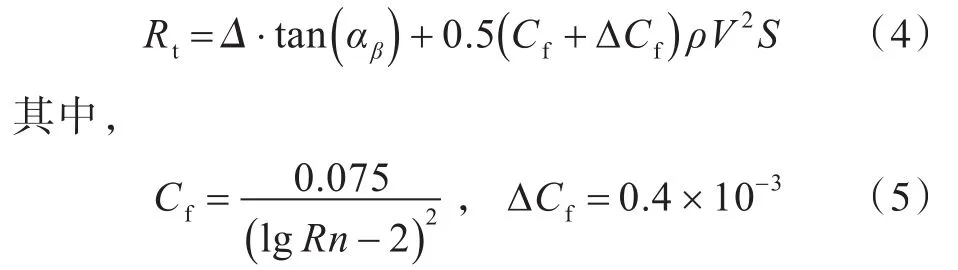
式中，Cf為摩擦阻力系數。

1.2.2 舒福德—勃朗法

采用舒福德—勃朗法計算滑行艇阻力的具體步驟如下：

1）已知艇重Δ，航速V，艇寬B，重心至艉板的水平距離ξg，計算艇寬傅氏數和升力系數

2）求解方程組（6），得到縱傾角α及浸濕長寬比λ。

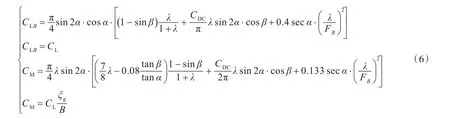
式中：CLB為計及勃朗修正的以船寬B為特征尺度的升力系數；CM為力矩系數；CDC為橫流阻力系數，考慮艇型實際情況，取CDC=4/3。

3）計算浸濕面積S=λB2/cosβ、浸濕長度I=λB和雷諾數Rn=V·I/ν。

4）計算總阻力：

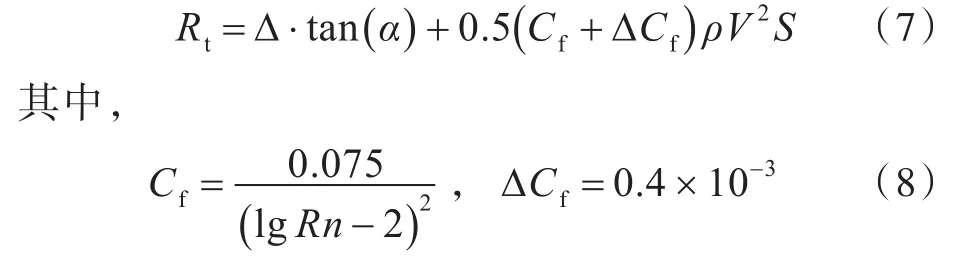
1.3 CFD數值計算方法

STAR CCM+是一款新型的CFD計算軟件，其功能包含了從幾何模型的建立、表面網格的準備、體網格的劃分、模型的設定、計算求解，一直到后處理分析的整個模擬過程，被廣泛應用于船舶水動力性能計算和模擬中，并取得了顯著成果。與以往采用重疊網格的方法不同，本文采用STAR CCM+軟件中的DFBI模塊對滑行艇模型阻力進行數值計算。該方法在計算排水型船舶阻力結果方面精度較高，但針對高速滑行狀態下的阻力計算，資料仍然較少。

1.3.1 控制方程

采用雷諾平均法進行數值求解。在笛卡爾坐標系下，張量指標形式下的時均連續方程和動量方程（Navier-Stokes方程）如下：

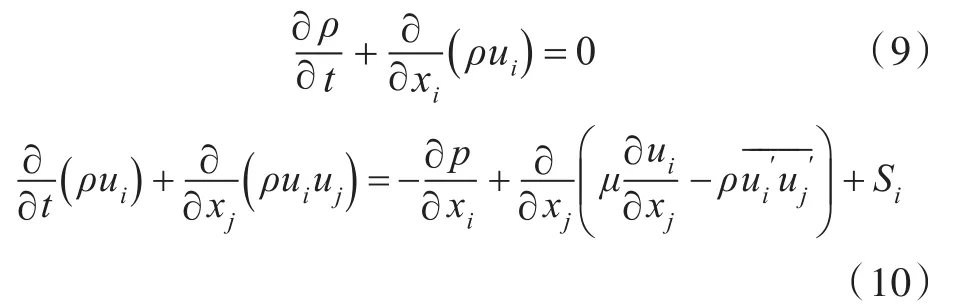
式中：i，j=1，2，3；μ為動粘性系數；xi，xj為笛卡爾坐標系下不同方向的分量；為速度分量脈動值；p為壓力時均值；Si為動量方程廣義源項；“—”表示對物理量取時間平均。

為使上述方程組封閉，需引入湍流模型（方程），此處選取Realizablek-ε兩方程模型。

1.3.2 計算域的建立及網格劃分

考慮到本文是對滑行艇直航阻力進行計算，以及艇體嚴格的對稱性，為減小計算量，選取半船模型進行數值模擬。構建的計算域如圖2所示。

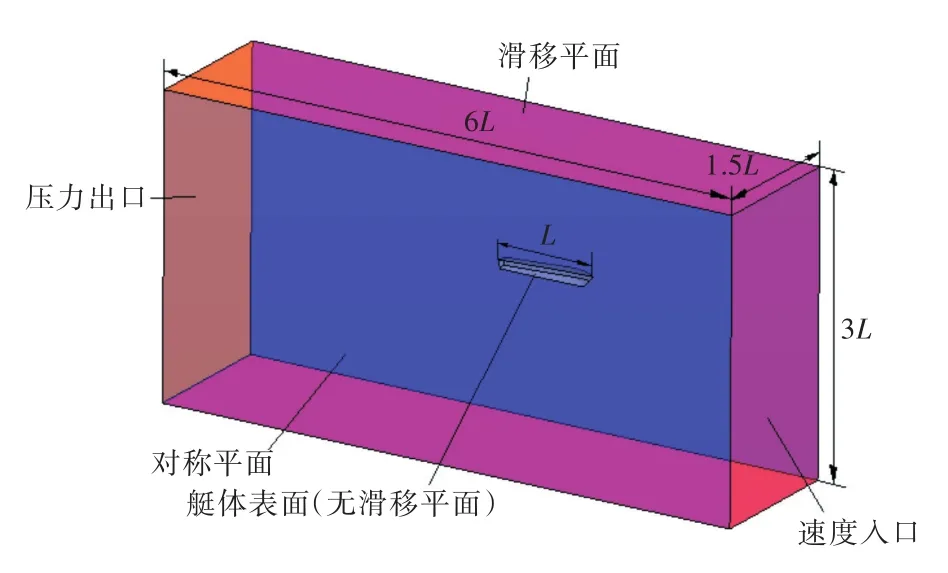
圖2 計算域Fig.2 Computational domain for the planing craft model

選擇切割體網格進行網格劃分，在艇體附近和自由面附近進行適當加密，并觀察網格質量是否符合要求。生成的艇體網格如圖3所示，其中陰影密集部分即為加密區域。

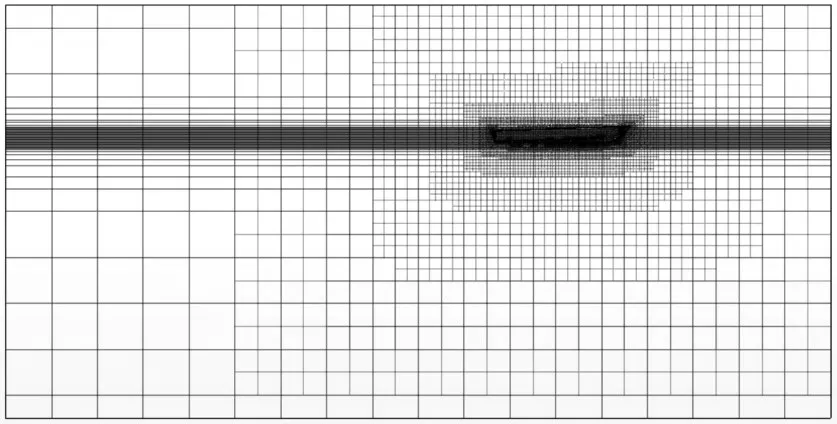
圖3 網格劃分Fig.3 Grid division of the planing craft model

1.3.3 物理模型的選取

STAR CCM+軟件提供的流體體積法（VOF）波模型可供使用。VOF波模型通過在整個計算域內對互不相溶的兩種流體求解同一組動量方程，并追蹤每種流體的體積分數來模擬多相流，以使得采用STAR CCM+軟件模擬船舶運動更簡便。選取歐拉多相流、VOF波和重力等模型來模擬滑行艇運動時的受力情況。

1.3.4 初始條件及邊界條件的設置

根據之前設置的VOF波模型相關場函數，設置流場的壓力、速度和體積分數等初始條件，并對計算域邊界的物理條件進行設定。

1.3.5 創建六自由體DFBI運動

選取DFBI模塊模擬滑行艇的運動，建立原點位于重心的船體坐標系，以使得在滑行艇運動模擬中艇體繞重心做升沉和縱傾運動。

2 計算結果對比分析

本文分別使用查潔法、舒福德—勃朗法和CFD方法計算了15個不同靜水速度（1.627，2.44，3.253，4.067，4.55，4.88，5.21，5.693，6.507，7.32，7.808，8.133，8.459，8.784和9.10 m/s）下同一滑行艇模型的阻力，并進行了船模阻力試驗以驗證所得結果。

2.1 船模阻力試驗

船模阻力試驗在中國特種飛行器研究所進行，根據所設計的型線，制作了滑行艇模型，并采用拖曳法對其阻力、升沉及縱傾角等數據進行了測量和記錄。圖4所示為在8.133 m/s速度下的滑行艇運動情況。

圖4 滑行艇在拖曳水池中的運動情況Fig.4 Movement of the planing craft model in towing tank

2.2 半理論半經驗方法計算結果對比分析

通過運用前述的半理論半經驗方法，基于1.1節中給出的模型參數，計算得到的模型總阻力值Rt與試驗值的對比如圖5所示，縱傾角的對比如圖6所示。圖中，F▽為體積傅汝德數。

由圖5可以看出，在整個速度區間內，半理論半經驗方法的阻力計算結果的總體變化趨勢均能與試驗值大體保持一致；在高速滑行區間（F▽＞3.0），采用查潔法和舒福德—勃朗法均能較好地對滑行艇阻力值進行計算。在該區間內，查潔法的阻力計算結果與試驗值更為接近，最大誤差為5.61%，最小誤差僅為0.11%，基本滿足工程應用要求；而在F▽=3～4范圍內，采用舒福德—勃朗法所得結果與試驗值比較一致。由圖6可以看出，采用半理論半經驗方法可以反映出滑行艇縱傾角大致的變化趨勢，但具體的計算結果與試驗值相差較大，在大部分速度下二者的差值均在1°左右；而查潔法與舒福德—勃朗法相比能更好地反映真實情況下縱傾角隨速度的變化。

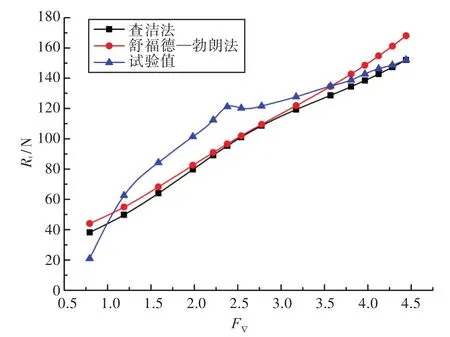
圖5 半理論半經驗方法阻力計算值與試驗值對比Fig.5 Comparison of the analytical-experimental method results and experimental values about resistances

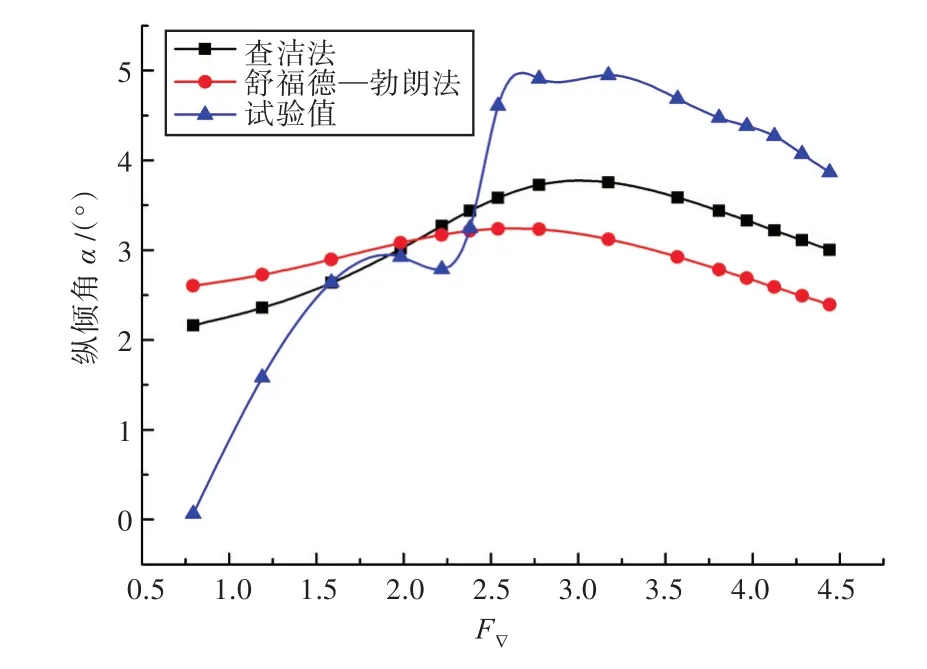
圖6 半理論半經驗方法縱傾角計算值與試驗值對比Fig.6 Comparison of the analytical-experimental method results and experimental values about trims

2.3 CFD方法計算結果對比分析

采用1.3節所述方法，使用STAR CCM+軟件對滑行艇模型阻力進行計算，所得結果與試驗值的對比如圖7所示，縱傾角的對比如圖8所示。

由圖7可見，采用CFD方法所得阻力計算值在大部分速度下與試驗值均能較好地吻合，在滑行艇進入高速滑行穩定狀態后，使用CFD方法可以達到較高的計算精度，其與試驗值的相對最大誤差為3.29%，且隨著速度的增大，其計算精度明顯提高，誤差逐漸減小，最小誤差僅為0.38%，符合工程應用標準。相比以往采用重疊網格的CFD滑行艇阻力計算方法，采用DFBI模塊的方法操作簡單，所需計算資源較少，同時阻力計算值也能獲得較高的計算精度，不過縱傾角的計算結果與試驗值相比誤差較大。

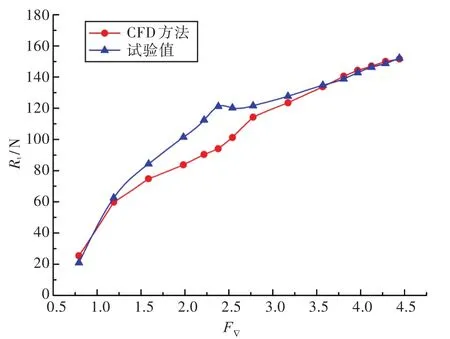
圖7 CFD方法阻力計算值與試驗值對比Fig.7 Comparison of the CFD method results and experimental values about resistances

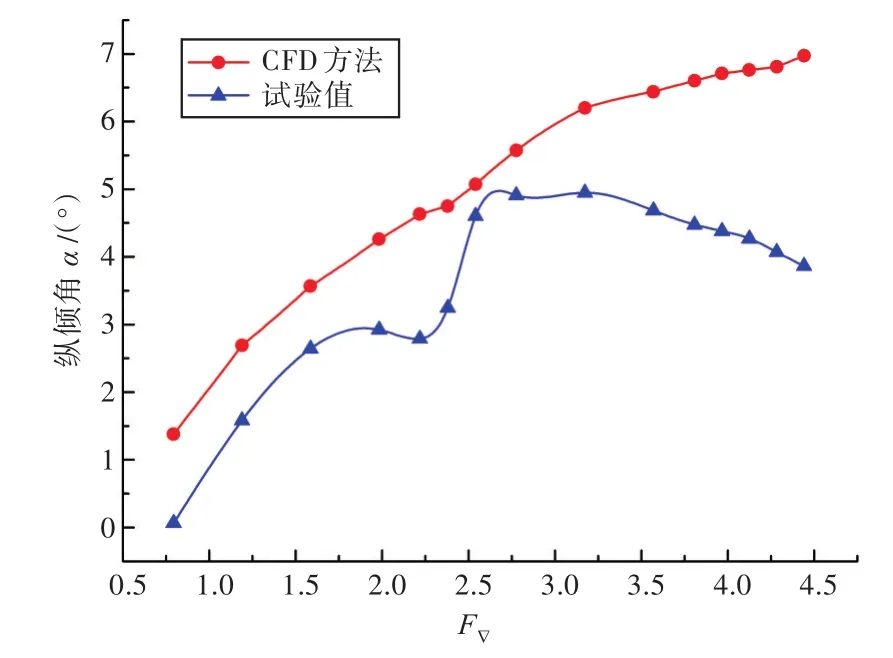
圖8 CFD方法縱傾角計算值與試驗值對比Fig.8 Comparison of the CFD method results and experimental values about trims

3 結 論

本文通過使用半理論半經驗方法和CFD方法對某滑行艇模型進行阻力計算，并進行船模試驗對比和驗證，得到以下結論：

1）在高速滑行區間（F▽＞3.0），采用半理論半經驗方法得到的總阻力計算結果可滿足工程應用要求，其中采用查潔法的總阻力計算結果要優于采用舒福德—勃朗法的結果，采用舒福德—勃朗法的阻力計算結果僅在F▽=3～4范圍內與試驗值比較一致。縱傾角計算值的變化趨勢與試驗值相近，誤差在1°左右。

2）基于STAR CCM+軟件中的DFBI模塊，采用CFD數值計算方法在大部分速度下均能得到較好的總阻力計算結果，且在高速滑行狀態下可以達到較高的計算精度，但縱傾角的計算結果誤差較大，仍有待改進。

本文的研究表明，基于STAR CCM+軟件DFBI模塊的CFD數值計算方法可以較好地實現該滑行艇型的阻力計算，并將進一步應用于后續相關滑行艇的阻力計算。在今后的工作中，將針對網格單元等因素對滑行艇阻力計算的影響進行研究，目前正在進行之中。