船舶運動與液艙晃蕩耦合頻域計算方法

孫雷，羅賢成，劉昌鳳，姜勝超

1大連理工大學船舶工程學院，遼寧大連116024

2高新船舶與深海開發裝備協同創新中心，上海200240

3大連海洋大學海洋與土木工程學院，遼寧大連116023

0 引 言

船舶運動與液艙內流體的晃蕩會產生相互作用，特別是對于液化天然氣船（LNG）和浮式生產儲油卸油設備船（FPSO）等含有大型液艙的船舶，其具有較大的液艙，并且液艙的固有頻率接近于船舶運動頻率，會導致液艙內流體產生的晃蕩作用更加明顯。因此，在載液船舶的設計初期，就應該考慮船舶運動與液艙內流體晃蕩的耦合作用影響。近年來，有關船舶與液艙晃蕩耦合作用的研究已有較大進展。Francescutto和 Contento［1］通過對載液船舶在橫浪工況下進行規則波作用下的模型實驗，證明液艙內液體晃蕩自由面的存在會對船舶運動產生影響。Rognebakke等［2］通過對液艙進行橫蕩實驗，獲得了穩定狀態下液艙橫蕩運動與線性入射波頻率之間的線性關系。Molin等［3］通過計算載有液艙的LNG船，得到了船舶運動與艙內液體自由水面的變化情況。Newman［4］開發的WAMIT程序可用于計算線性液艙晃蕩與船舶運動耦合情況。KIM等［5］采用脈沖響應函數（IRF）求解線性船舶運動，采用有限差分方法模擬非線性液艙的晃蕩問題，并與載有方形液艙的S175船舶橫搖運動實驗結果進行了對比，結果顯示吻合較好。操戈等［6］考慮了液艙內流體的粘性，發現所得結果與試驗值更接近。

本文將采用頻域計算方法研究船舶運動與液艙晃蕩耦合作用問題。在頻域方法中，對于船舶運動方程，采用自由面格林函數方法進行求解；對于液艙內流體晃蕩過程，采用Rankine源方法進行求解。為提高計算精度，本文將采用高階邊界元方法進行離散，應用8節點等參數單元進行頻域求解，并以文獻［7］中裝載2個液艙的船舶模型為例，將本文計算結果與采用水動力軟件HYDROSTAR所得結果、文獻［8］的數值計算結果及文獻［7］的實驗數據進行對比，以驗證本文計算方法的準確性。

1 運動預報理論

1.1 船舶運動

船舶在波浪上的運動預報是研究船舶運動與液艙流體晃蕩的基礎，且波浪幅值與船舶特征尺度相比是小量，流體的粘性影響很小，波浪繞射力對船舶影響較大。因此，在研究船舶在波浪中的運動姿態時，基于勢流理論，流體通常可以假設為均勻、不可壓縮、無粘、無旋的理想流體。

波浪中的參考坐標系如圖1所示。其中，固定坐標系為大地坐標系o0-x0y0z0，平面x0o0y0與船舶靜水面重合，o0z0軸垂直向上；船舶位置參考系為o′-x′y′z′，o′x′軸位于中縱剖面，指向船艏為正，o′y′軸指向右舷為正，o′z′軸垂直向上；船舶動坐標系為o-xyz，oz軸垂直向上，當船有航速時，該坐標系隨船以平均速度移動，代表著船舶運動形態。

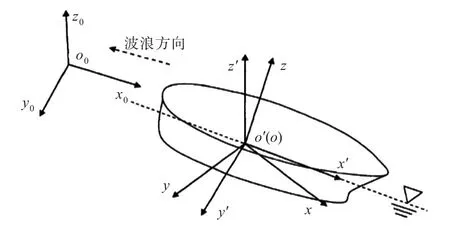
圖1 船舶運動坐標系Fig.1 The coordinate system for ship motions

根據三維線性勢流理論，采用一階近似，分布在船舶周圍的速度勢函數滿足線性邊界條件與拉普拉斯方程。當船舶靜止在自由水面上搖蕩時（無航速），流場中的一階不定常速度勢?可以分解為

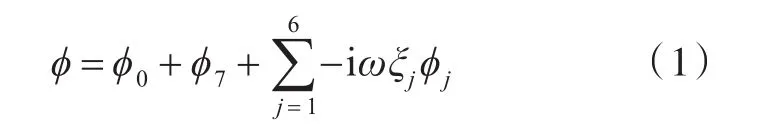
式中：?0為入射勢；?7為繞射勢；?j為j自由度上的輻射勢；ω為波浪圓頻率；ξj為在j自由度上的位移；i為虛數單位。

入射勢可取AIRY線性波，繞射勢與輻射勢的規范化定解條件滿足拉普拉斯方程（式（2））與邊界條件（式（3）和式（4））。

在船體表面SB上，

在自由水面SF上，

式中：g為重力加速度；n為網格單元垂直方向；j為各個自由度。

應用格林第二定理，將源點布置在船體表面，并在船體表面建立邊界積分方程：

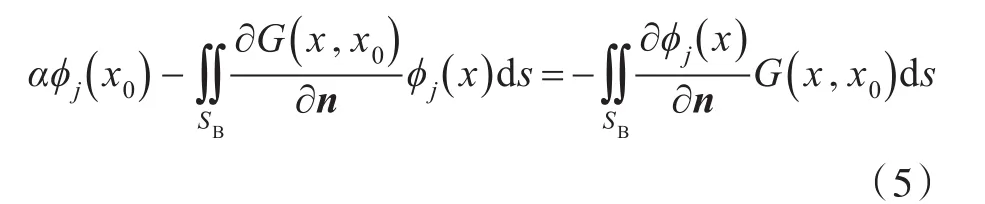
式中：α為自由項系數（固角系數），對于常單元，α=1/2，對于高階邊界元，α隨體表面變化；G為自由面格林函數，也即Havelock源格林函數。

本文采用邊界元法將頻域內的積分簡化為僅在船體表面積分，大大減小了計算時間和數據存儲時間，并采用高階邊界元法離散上述積分方程，使表面離散成等參數單元，然后代入積分方程進行求解，便可得到速度勢大小。得到速度勢值后，在船體瞬時濕表面上進行伯努利積分，便可得到船舶濕表面瞬時波浪載荷

式中：fex為波浪激振力矩陣；fhydro為輻射力矩陣；frestor為回復力矩陣；μ為附加質量矩陣；λ為輻射阻尼系數矩陣；C為靜回復力系數矩陣；ξ為船舶位移矩陣。

獲得船舶水動力系數后，可建立船舶運動方程（式（7）），得到船舶在各個自由度上的運動位移

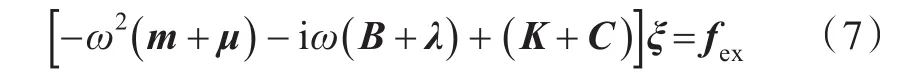
式中：m為廣義質量矩陣；B為船舶系統阻尼矩陣；K為船舶系統剛度矩陣。

1.2 液艙流體晃蕩

研究艙內流體的流動時，選取如圖2所示的坐標系。液艙計算用動坐標系o-xyz，原點位于艙內自由水面中心；參考坐標系o′-x′y′z′不隨物體而搖晃，當物體處于平衡位置時，其與動坐標系重合；固定坐標系o0-x0y0z0固定于空間某點，不隨模型運動而變化。基于線性勢流理論，艙內流體運動滿足拉普拉斯方程與以下邊界條件。

在液艙壁面ST上，

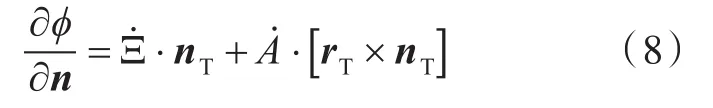
在自由水面SF上，

在船體表面SB上，

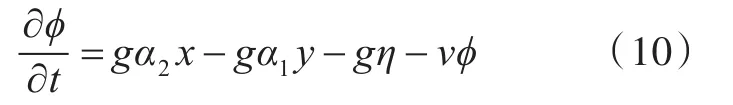
式中：Ξ =（ξ1，ξ2，ξ3），為液艙平動位移（動坐標系相對于參考坐標系）；A=（α1，α2，α3），為液艙轉動位移（動坐標系相對于參考坐標系）；rT為位置矢量（相對于參考坐標系原點）；nT為方向矢量；η為艙內液體波面升高；v=ωk，為考慮自由水面的阻尼系數［9］，其中k為經驗系數。

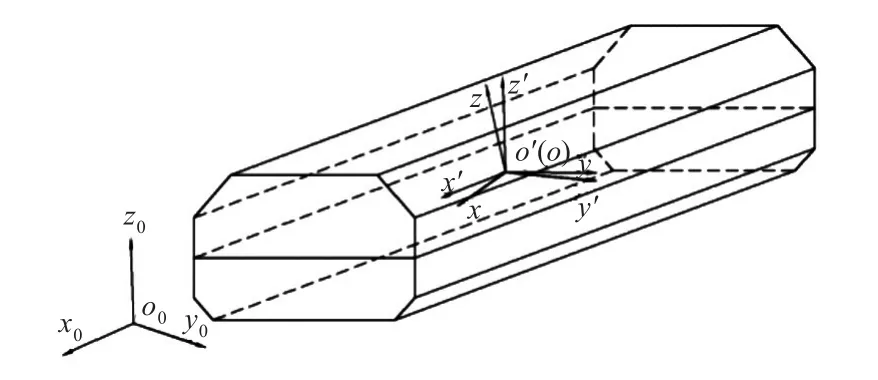
圖2 液艙運動坐標系Fig.2 The coordinate system of the tank

根據線性關系，可將速度勢函數進行分解：

液艙的邊界條件可以寫為：

在液艙壁面ST上，

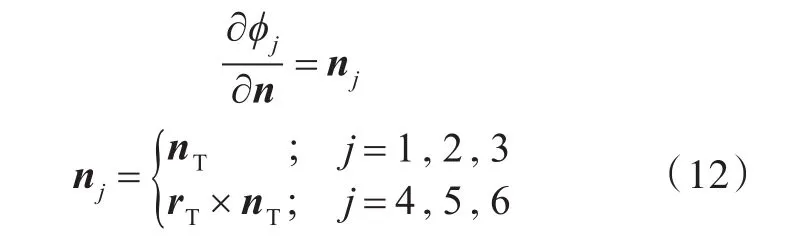
在自由水面SF上，

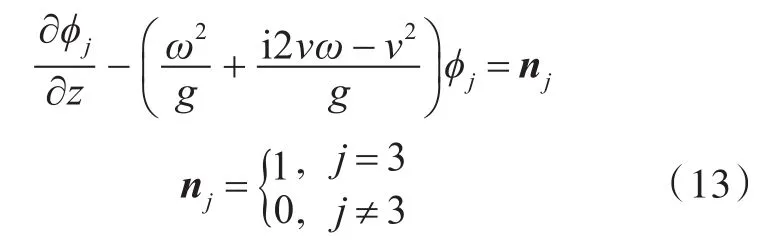
應用格林定理，建立邊界積分方程：

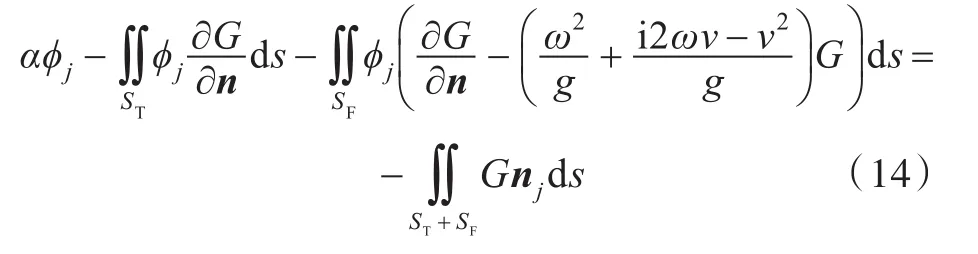
式中，G為格林函數，為簡便計算，采用簡單Rankine源格林函數。

同樣，采用高階邊界元法對上述積分方程進行離散求解，可以得到速度勢。將速度勢代入伯努利方程，沿著艙內瞬時濕表面進行積分，便可得到艙內波浪激振力

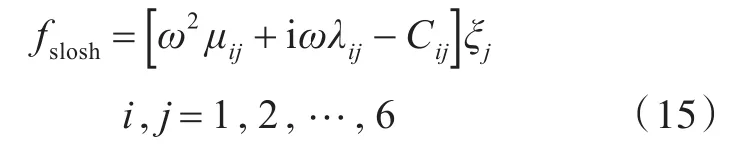
1.3 船舶運動與液艙流體晃蕩耦合作用

通過上述研究，綜合考慮船舶運動與液艙晃蕩影響，建立頻域運動下船舶與液艙晃蕩耦合運動方程為

式中：μext為外部波浪激勵的附加質量矩陣；μslosh為液艙流體晃蕩的附加質量；Bext為外部波浪激勵的阻尼矩陣；Bslosh為液艙流體晃蕩的阻尼矩陣；Cext為外部波浪激勵的靜回復力系數矩陣；Cslosh為液艙流體晃蕩的靜回復力系數矩陣。

本文考慮兩者耦合作用計算的流程圖如圖3所示。

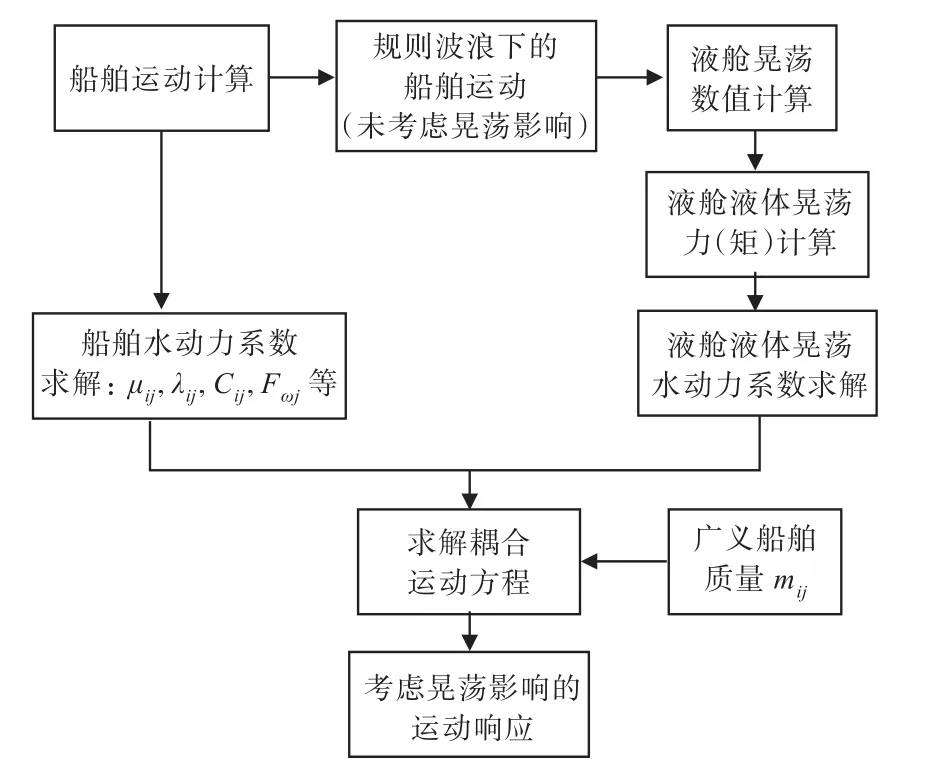
圖3 計算流程示意圖Fig.3 Flow chart for numerical simulation

2 驗證計算

2.1 波浪與三維結構物作用

本文以某艘FPSO船型為例，計算在規則波浪中，船舶在各自由度上的運動幅值響應算子（RAO），并將本程序計算結果與采用HYDROSTAR，AQWA軟件等計算的結果進行了對比，以驗算本程序計算的準確性。

2.1.1 計算模型

該計算船型的主尺度參數如表1所示，網格模型如圖4所示。

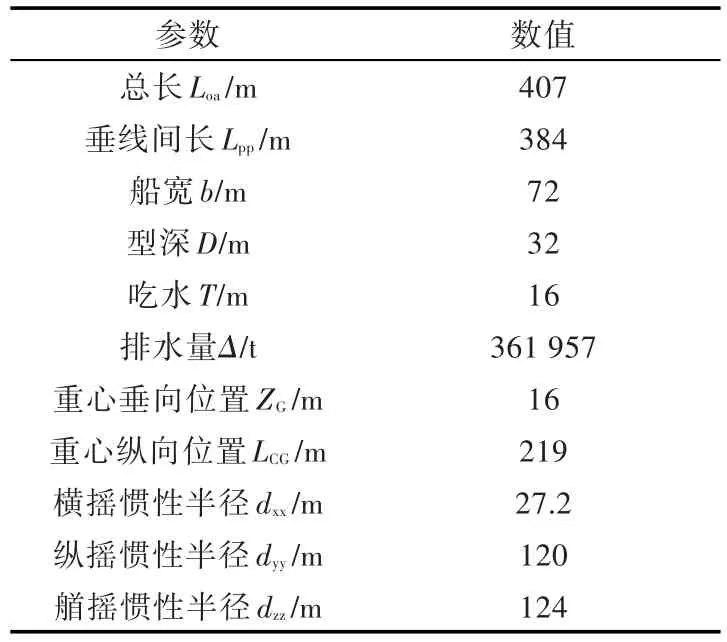
表1 FPSO船型主尺度參數Table 1 The main parameters of FPSO ship

圖4 船體網格計算模型Fig.4 The computational model of ship

2.1.2 計算結果與分析

選取橫浪（波浪與船艏方向夾角為90°）與迎浪（波浪與船艏方向夾角為180°）這2種工況，用本程序計算船舶在規則波作用下的運動響應，并分別與HYDROSTAR和AQWA軟件計算的水動力計算結果進行對比，結果如圖5～圖8所示。圖中，PRESENT指本文計算結果，HYDROSTAR指采用HYDROSTAR軟件計算的結果，AQWA指采用AQWA軟件計算的結果，圖中縱坐標分別為3個自由度上的運動幅值響應算子［10］。

圖5 90°浪向下橫搖運動響應Fig.5 Rolling RAO in 90°wave direction angle

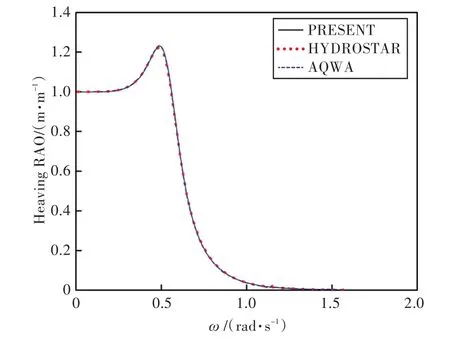
圖6 90°浪向下垂蕩運動響應Fig.6 Heaving RAO in 90°wave direction angle

圖7 180°浪向下縱搖運動響應Fig.7 Pitching RAO in 180°wave direction angle

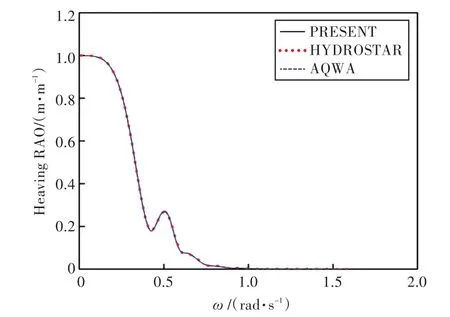
圖8 180°浪向下垂蕩運動響應Fig.8 Heaving RAO in 180°wave direction angle

圖9～圖14所示為橫浪作用下船舶6個自由度上的波浪激振力（力矩）對比。

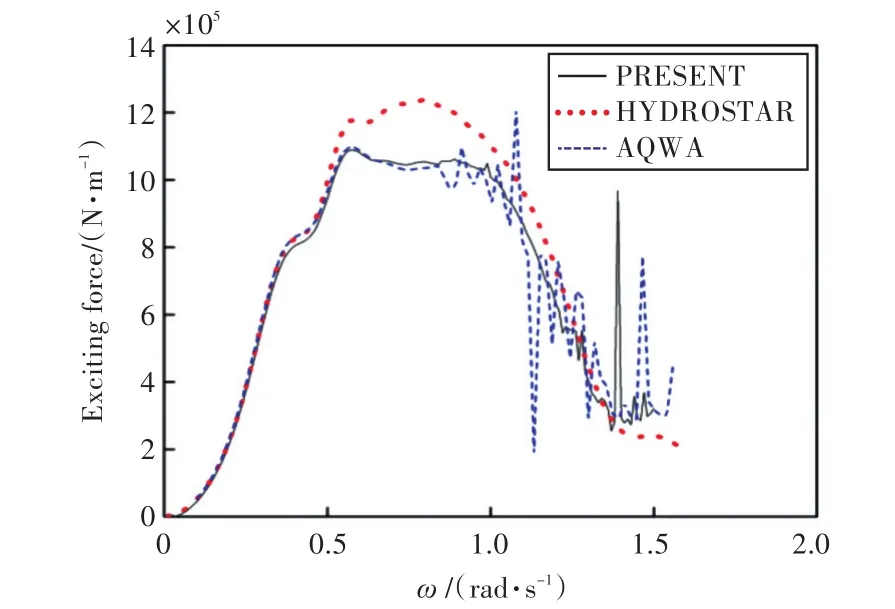
圖9 x軸的波浪激振力Fig.9 Wave exciting force in the x axis

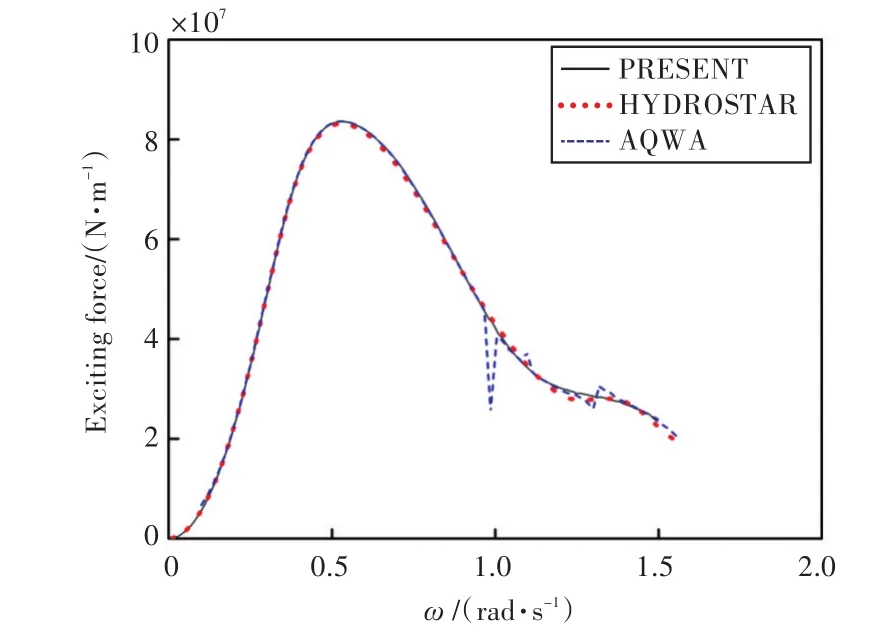
圖10 y軸的波浪激振力Fig.10 Wave exciting force in the y axis

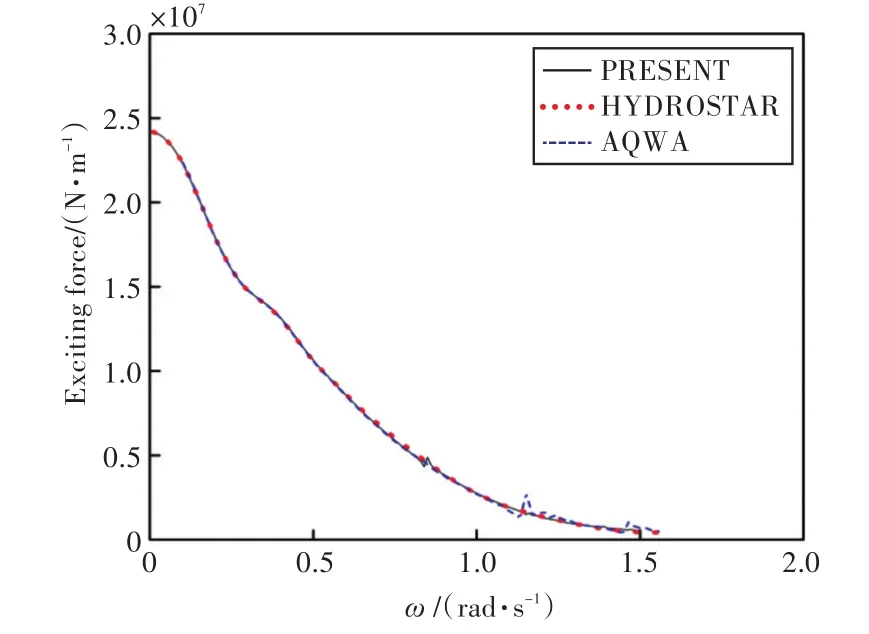
圖11 z軸的波浪激振力Fig.11 Wave exciting force in the z axis

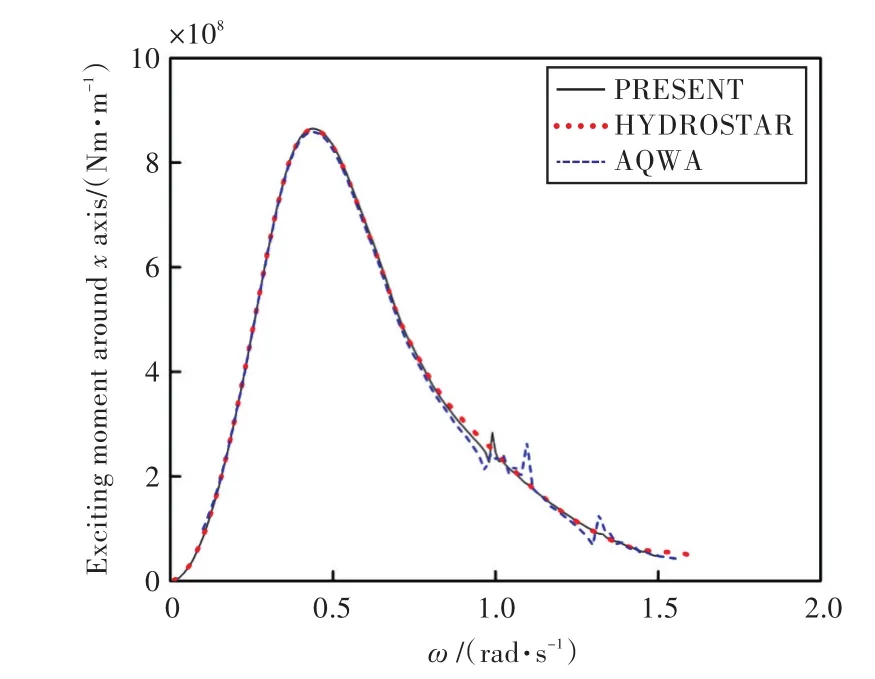
圖12 繞x軸的波浪激振力矩Fig.12 Wave exciting moment around the x axis

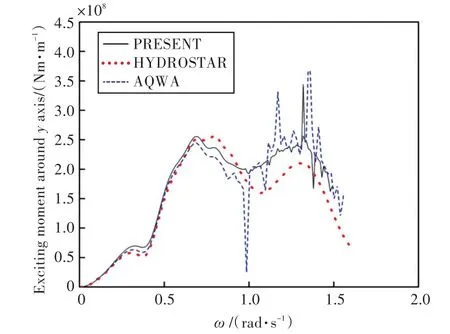
圖13 繞y軸的波浪激振力矩Fig.13 Wave exciting moment around the y axis

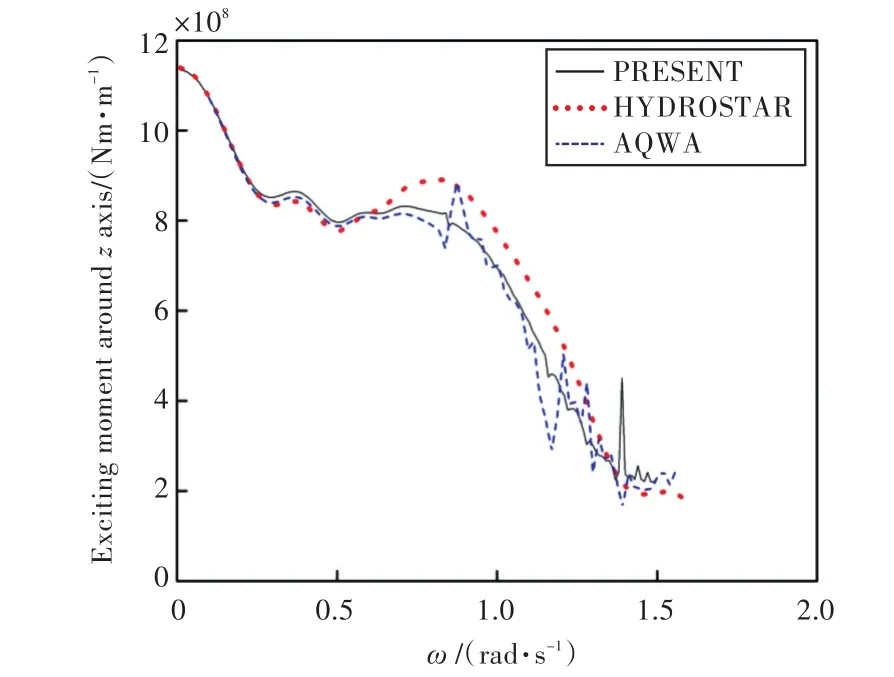
圖14 繞z軸的波浪激振力矩Fig.14 Wave exciting moment around the z axis

由圖可知，本文程序計算所得船舶在各自由度上的運動響應和波浪激振力與HYDROSTAR和AQWA水動力軟件計算的結果吻合較好，證實了本文計算程序的準確性，也為下文進行船舶與液艙晃蕩耦合運動提供了較好的基礎。

2.2 考慮液艙晃蕩的船舶運動

本文以某艘帶2個液艙的FPSO船型為例，分別計算前、后液艙在不同裝載率下的運動響應。

2.2.1 計算模型

選取的計算船型與液艙的主尺度參數分別如表2和表3所示。該船型與液艙（左艙為前艙）的平面視圖如圖15所示（圖中數值單位為m），網格計算模型如圖16所示。

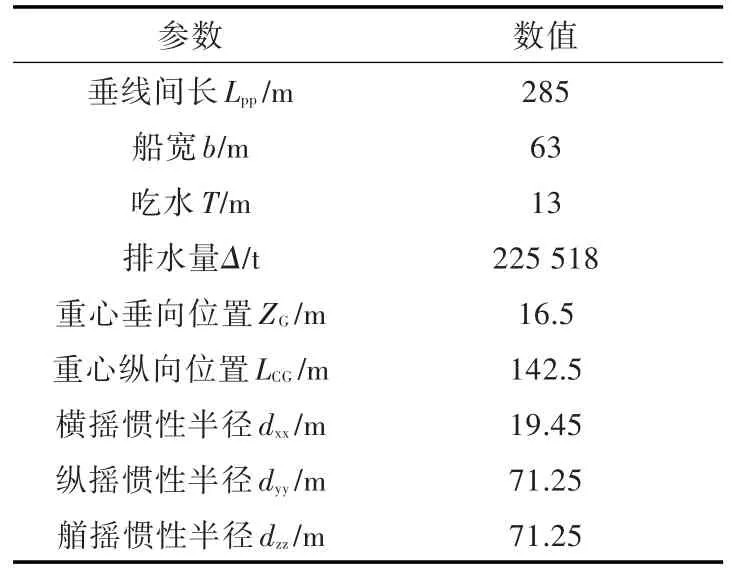
表2 FPSO船型主尺度參數（帶2個液艙）Table 2 The main parameters of FPSO ship with two tanks

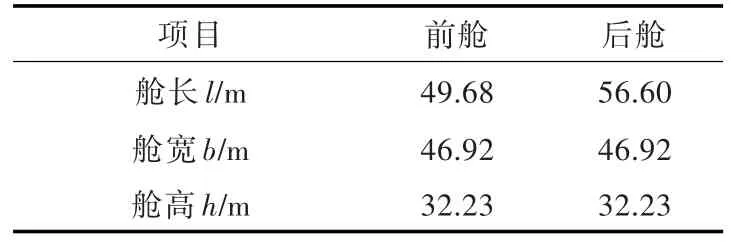
表3 液艙主尺度參數Table 3 The main parameters of the tank

圖15 船型與液艙的平面視圖Fig.15 The plane view of the ship and tanks

圖16 船型與液艙耦合網格計算模型Fig.16 The computational model of the ship and tanks

2.2.2 計算結果與分析

本文選取裝載液體為水，計算無液艙裝載（裝載率為0）以及前、后液艙裝載率分別為（20%，20%），（30%，30%）和（57.5%，43.3%）時，船舶在浪向為 90°，120°，180°時各自由度下的運動幅值響應算子（基于船舶重心處），并與水動力軟件HYDROSTAR計算結果、文獻［8］的數值模擬結果以及文獻［7］的實驗數據進行對比，計算結果如下。

圖17～圖22所示為該該耦合船舶在無裝載情況下，浪向分別為 90°，120°和 180°時的運動響應幅值。

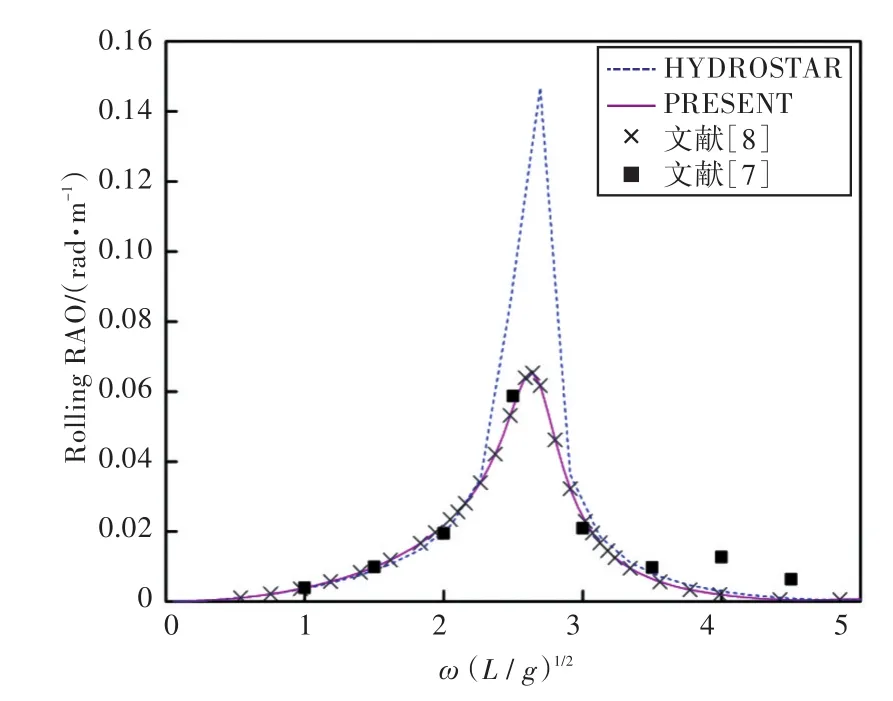
圖17 90°浪向下橫搖運動響應（無裝載）Fig.17 Rolling RAO in 90°wave direction angle（0 filling）

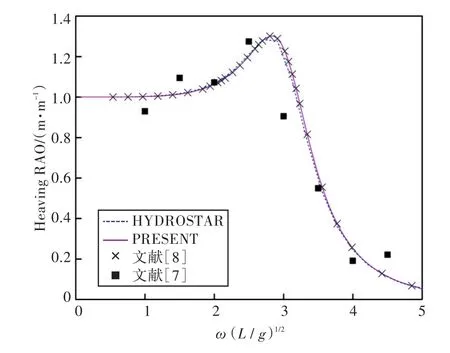
圖18 90°浪向下垂蕩運動響應（無裝載）Fig.18 Heaving RAO in 90°wave direction angle（0 filling）

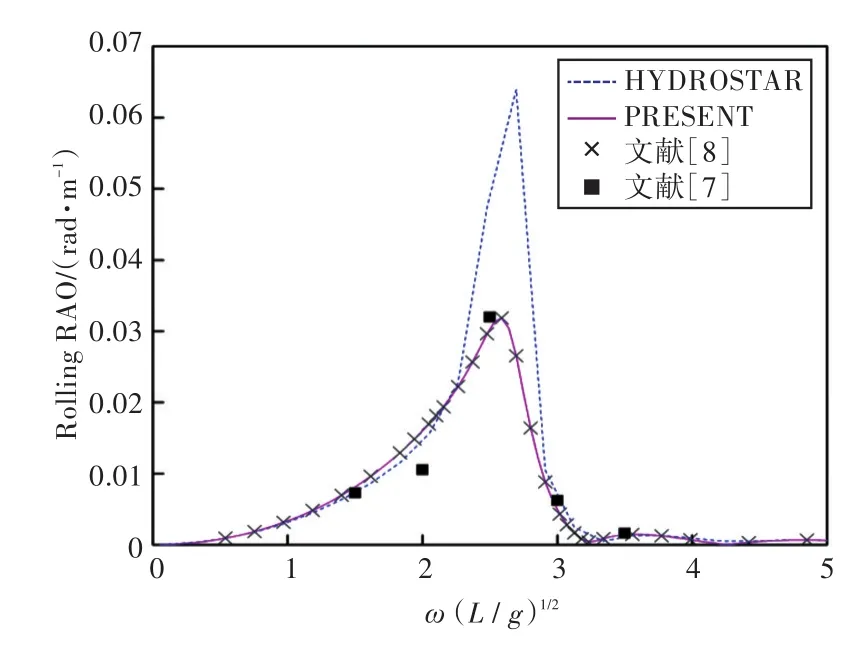
圖19 120°浪向下橫搖運動響應（無裝載）Fig.19 Rolling RAO in 120°wave direction angle（0 filling）

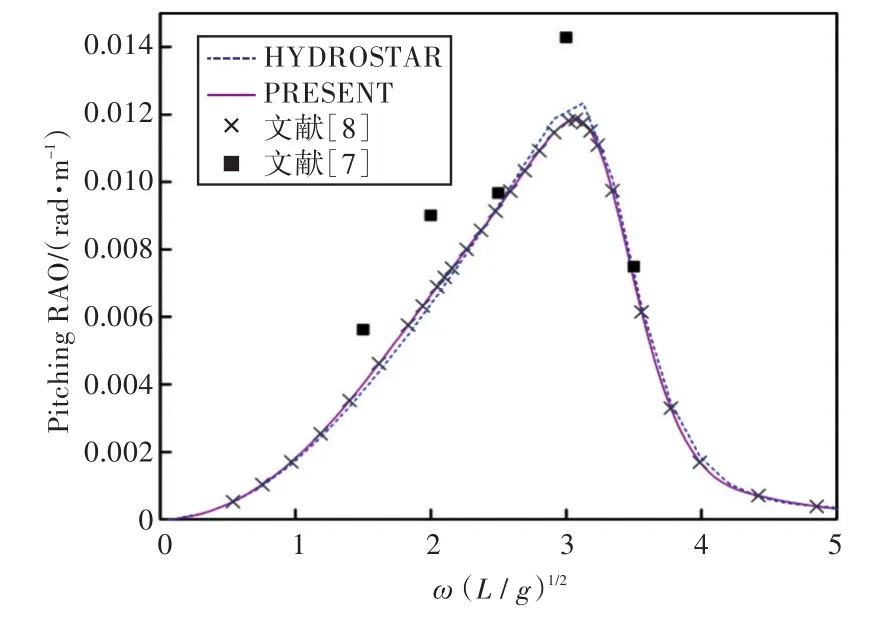
圖20 120°浪向下縱搖運動響應（無裝載）Fig.20 Pitching RAO in 120°wave direction angle（0 filling）

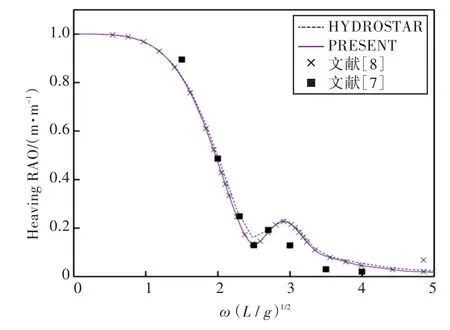
圖21 180°浪向下垂蕩運動響應（無裝載）Fig.21 Heaving RAO in 180°wave direction angle（0 filling）

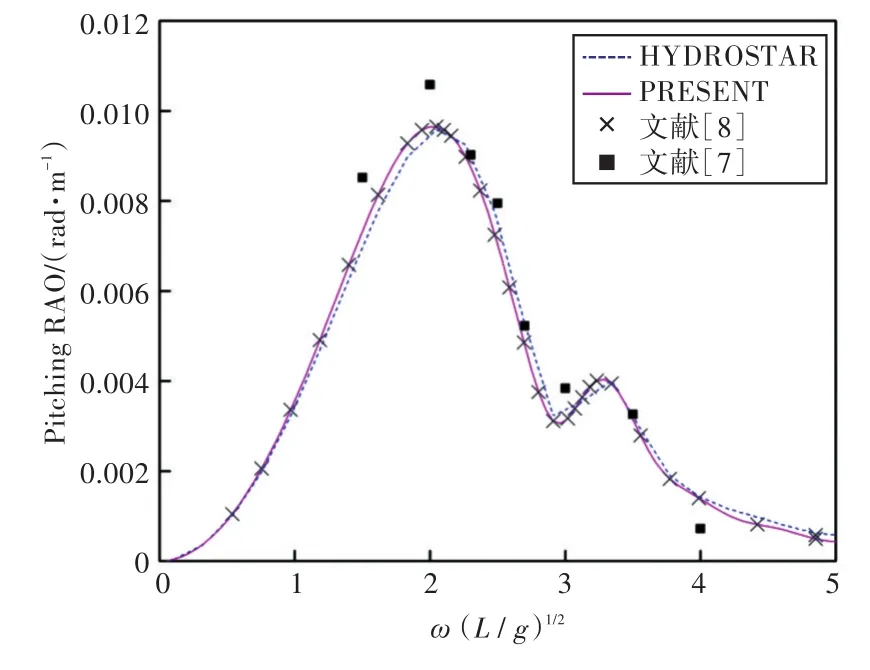
圖22 180°浪向下縱搖運動響應（無裝載）Fig.22 Pitching RAO in 180°wave direction angle（0 filling）

圖23～圖28所示為該耦合船舶在前、后艙裝載率為（20%，20%）情況下，浪向分別為90°，120°和180°時的運動響應幅值。

圖29～圖34所示為該耦合船舶在前、后艙裝載率為（30%，30%）情況下，浪向分別為90°，120°和180°時的運動響應幅值。

圖35～圖40所示為該耦合船舶在前、后艙裝載率為（57.5%，43.3%）情況下，浪向分別為90°，120°和180°時的運動響應幅值。

圖41所示為在90°浪向下，該耦合船舶在液艙不同裝載率下的橫搖運動響應對比圖。

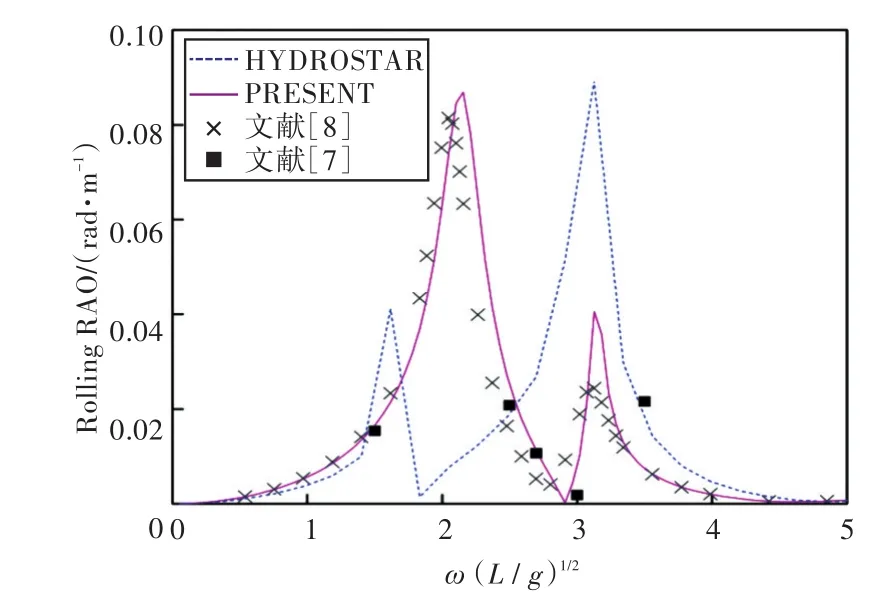
圖23 90°浪向下橫搖運動響應（前、后艙裝載率為20%，20%）Fig.23 Rolling RAO in 90°wave direction angle（filling ratio of fore and back tank is 20%，20%）

圖24 90°浪向下垂蕩運動響應（前、后艙裝載率為20%，20%）Fig.24 Heaving RAO in 90°wave direction angle（filling ratio of fore and back tank is 20%，20%）

圖25 120°浪向下橫搖運動響應（前、后艙裝載率為20%，20%）Fig.25 Rolling RAO in 120°wave direction angle（filling ratio of fore and back tank is 20%，20%）

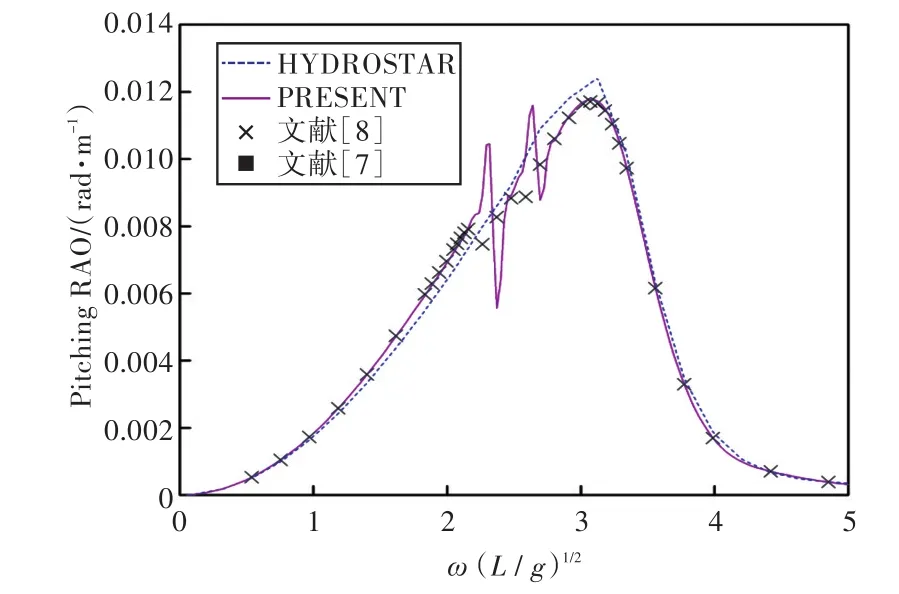
圖26 120°浪向下縱搖運動響應（前、后艙裝載率為20%，20%）Fig.26 Pitching RAO in 120°wave direction angle（filling ratio of fore and back tank is 20%，20%）

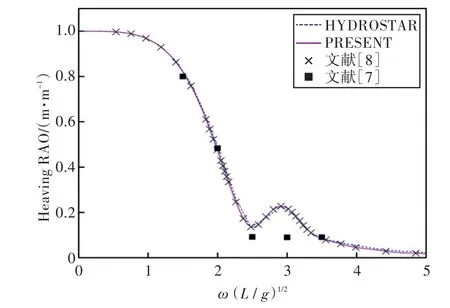
圖27 180°浪向下垂蕩運動響應（前、后艙裝載率為20%，20%）Fig.27 Heaving RAO in 180°wave direction angle（filling ratio of fore and back tank is 20%，20%）

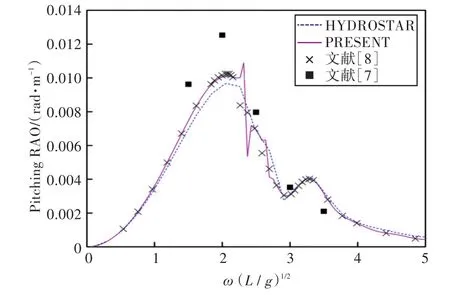
圖28 180°浪向下縱搖運動響應（前、后艙裝載率為20%，20%）Fig.28 Pitching RAO in 180°wave direction angle（filling ratio of fore and back tank is 20%，20%）

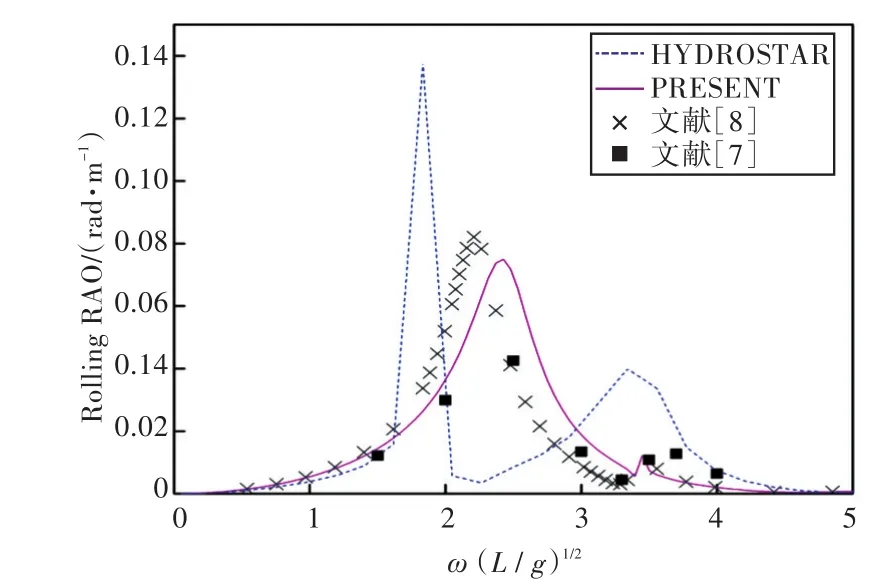
圖29 90°浪向下橫搖運動響應（前、后艙裝載率為30%，30%）Fig.29 Rolling RAO in 90°wave direction angle（filling ratio of fore and back tank is 30%，30%）

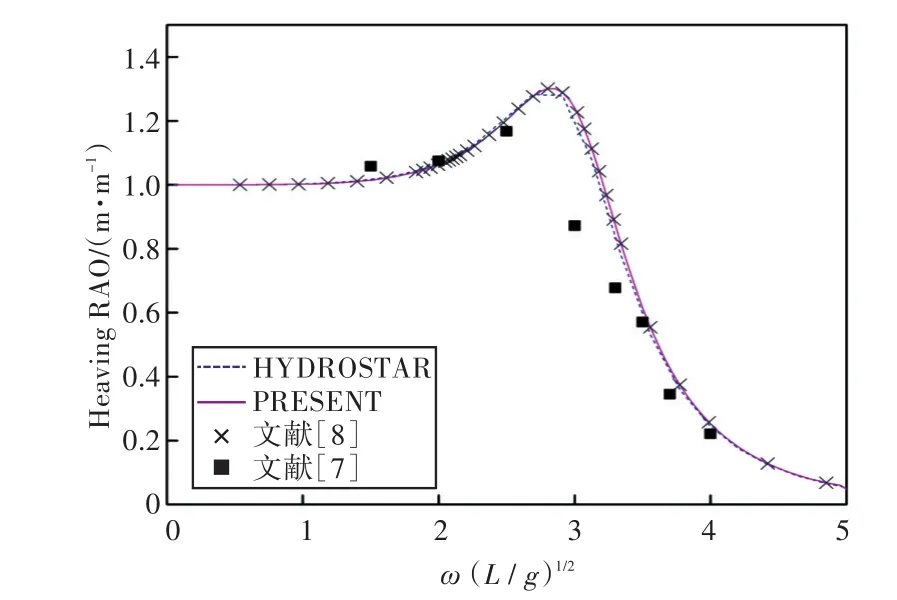
圖30 90°浪向下垂蕩運動響應（前、后艙裝載率為30%，30%）Fig.30 Heaving RAO in 90°wave direction angle（filling ratio of fore and back tank is 30%，30%）

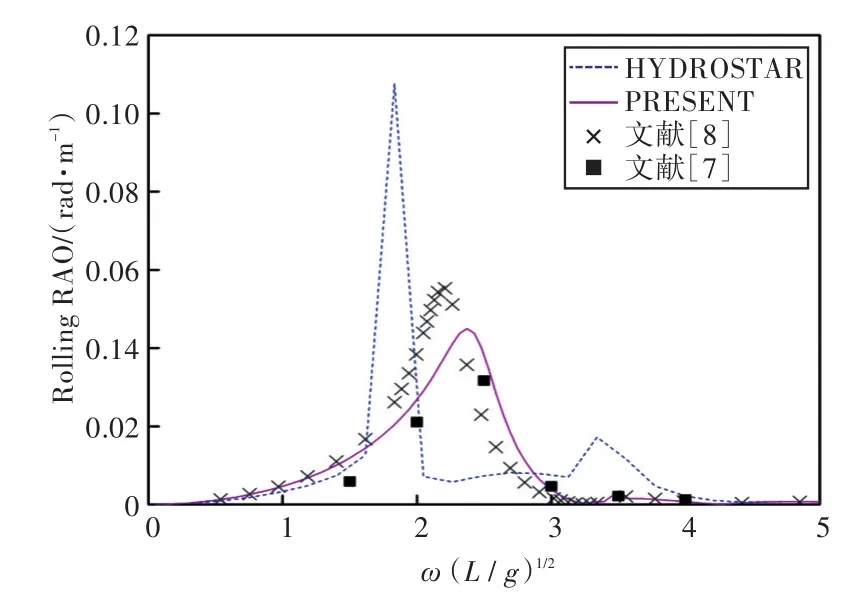
圖31 120°浪向下橫搖運動響應（前、后艙裝載率為30%，30%）Fig.31 Rolling RAO in 120°wave direction angle（filling ratio of fore and back tank is 30%，30%）

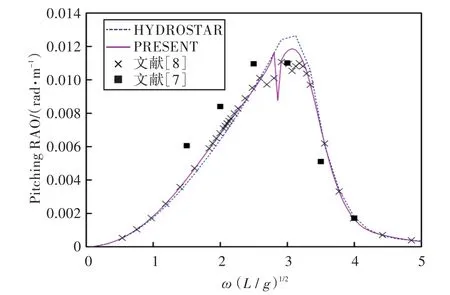
圖32 120°浪向下縱搖運動響應（前、后艙裝載率為30%，30%）Fig.32 Pitching RAO in 120°wave direction angle（filling ratio of fore and back tank is 30%，30%）

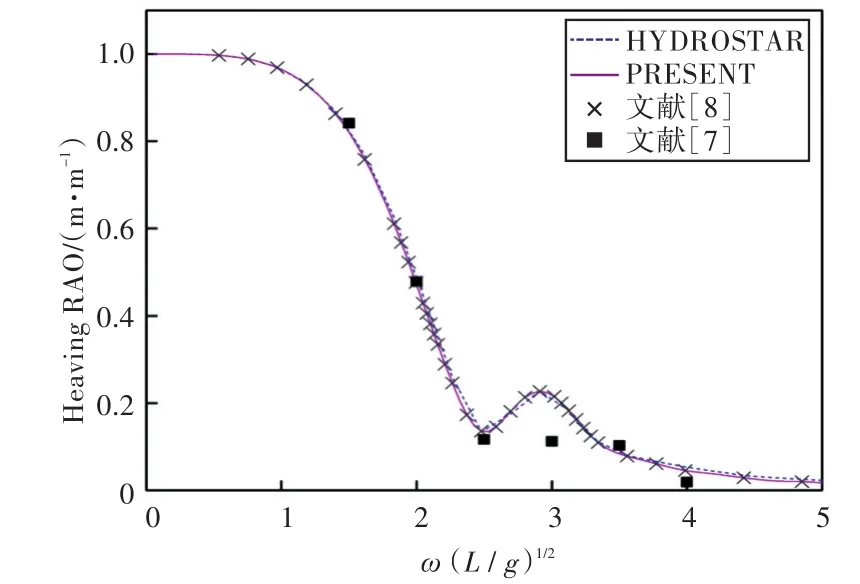
圖33 180°浪向下垂蕩運動響應（前、后艙裝載率為30%，30%）Fig.33 Heaving RAO in 180°wave direction angle（filling ratio of fore and back tank is 30%，30%）

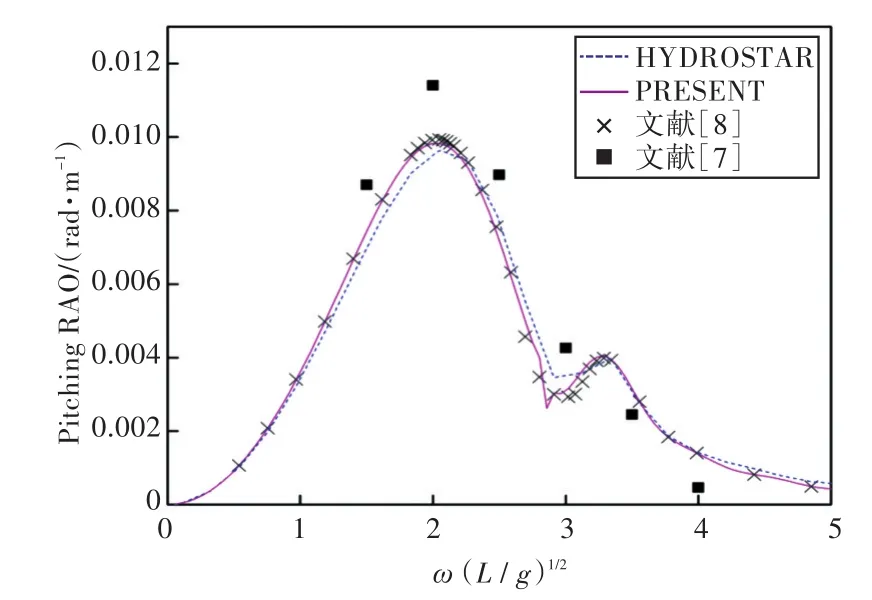
圖34 180°浪向下縱搖運動響應（前、后艙裝載率為30%，30%）Fig.34 Pitching RAO in 180°wave direction angle（filling ratio of fore and back tank is 30%，30%）

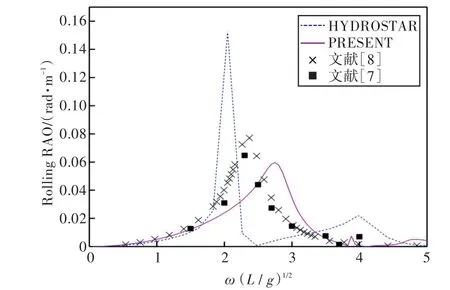
圖35 90°浪向下橫搖運動響應（前、后艙裝載率為57.5%，43.3%）Fig.35 Rolling RAO in 90°wave direction angle（filling ratio of fore and back tank is 57.5%，43.3%）

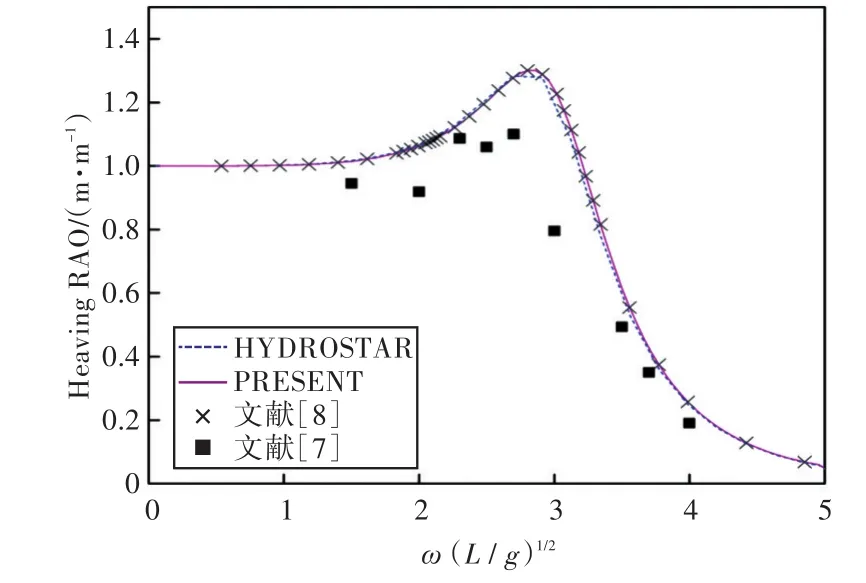
圖36 90°浪向下垂蕩運動響應（前、后艙裝載率為57.5%，43.3%）Fig.36 Heaving RAO in 90°wave direction angle（filling ratio of fore and back tank is 57.5%，43.3%）

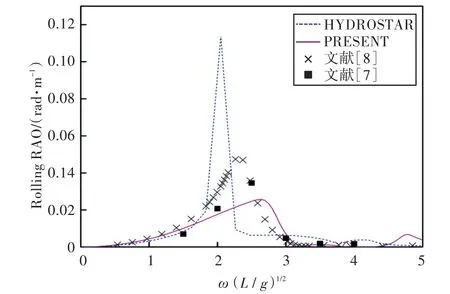
圖37 120°浪向下橫搖運動響應（前、后艙裝載率為57.5%，43.3%）Fig.37 Rolling RAO in 120°wave direction angle（filling ratio of fore and back tank is 57.5%，43.3%）

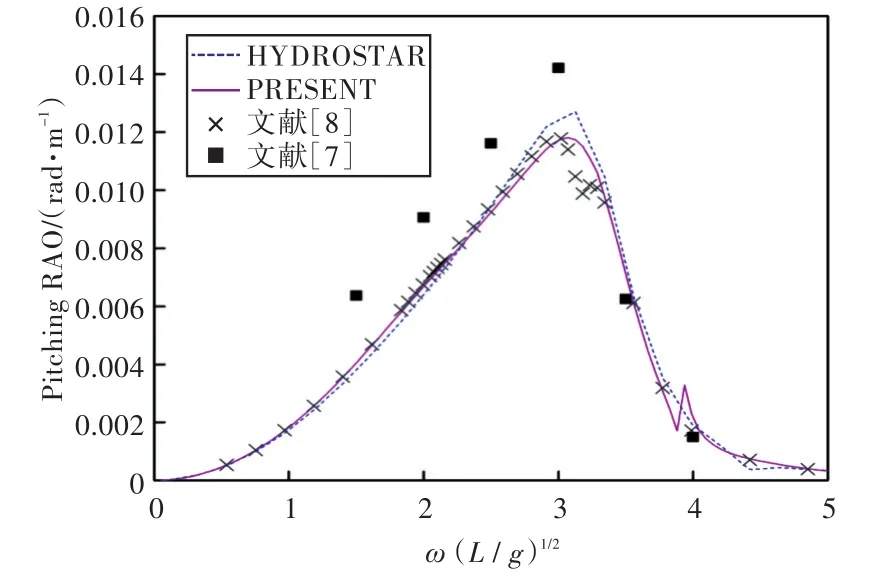
圖38 120°浪向下縱搖運動響應（前、后艙裝載率為57.5%，43.3%）Fig.38 Pitching RAO in 120°wave direction angle（filling ratio of fore and back tank is 57.5%，43.3%）

圖39 180°浪向下垂蕩運動響應（前、后艙裝載率為57.5%，43.3%）Fig.39 Heaving RAO in 180°wave direction angle（filling ratio of fore and back tank is 57.5%，43.3%）

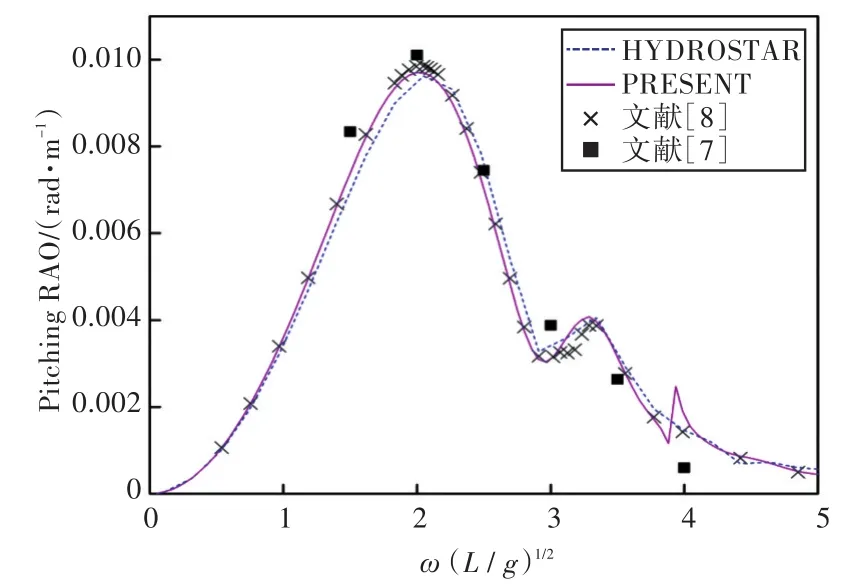
圖40 180°浪向下縱搖運動響應（前、后艙裝載率為57.5%，43.3%）Fig.40 Pitching RAO in 180°wave direction angle（filling ratio of fore and back tank is 57.5%，43.3%）

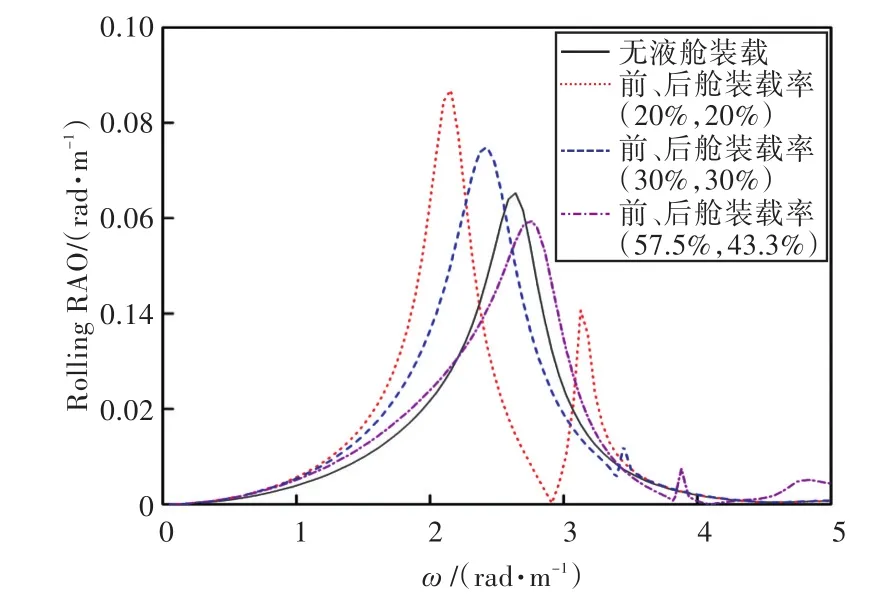
圖41 90°浪向下液艙不同裝載率下的橫搖運動響應Fig.41 Rolling RAO with different filling ratio in 90°wave direction angle

由以上圖中對比可以看出：

1）在船舶縱搖和垂蕩運動響應方面，以上4種計算結果均吻合較好，而在計算船舶橫搖運動響應時，幅值結果和共振頻率結果誤差較大。這主要是因為船舶縱、橫向尺寸比較大，因而在橫浪作用下橫搖運動較為劇烈。

2）當計算船舶橫搖運動響應時，在船舶和液艙共振頻率處，采用HYDROSTAR軟件計算的結果其幅值與其他計算結果相差較大，這可能是因為采用HYDROSTAR軟件計算的沒有考慮自由水面阻尼因素；而本文通過增加自由水面阻尼值，船舶橫搖運動響應和縱搖運動響應等計算結果均與實驗數據以及文獻［7］的數值計算結果吻合較好，這也證實了本文計算方法的正確性。

3）由上分析可知，船舶在橫浪（90°浪向）下的橫搖運動響應較劇烈。因此，通過對比橫浪作用下船舶在不同液艙裝載率情況下的橫搖運動響應可以發現，船舶的共振頻率出現了偏移，且當裝載率較低時，船舶的共振頻率偏于低頻，并隨裝載率的上升而向高頻方向移動。當液艙裝載液體時，船舶的橫搖運動出現了多個峰值，且當前、后液艙裝載率為（20%，20%）時，第2個峰值最大，說明此時液艙內流體晃蕩得最為劇烈；當裝載率高于或者低于此時的裝載率時，峰值又降低，說明液艙對船舶運動的影響存在一個“最佳”裝載率，在該裝載率下，液艙內的流體晃蕩對于船舶運動響應最大，在船舶設計時需著重予以注意。

3 結 語

本文通過頻域計算方法，對船舶在不同液艙液體裝載率情況下的運動響應進行了計算分析。首先，將本文計算結果與其他水動力軟件計算結果進行對比，驗證了本文計算船舶水動力系數程序的準確性。然后，計算了船舶耦合液艙晃蕩作用時的運動響應，將本文計算結果與實驗數據及已發表文獻的數值結果進行了對比，并采用HYDROSTAR軟件進行了計算。通過對比以上計算結果，證實了本文計算方法的正確性，并對結果數據進行了分析，指出了液艙晃蕩對船舶所造成的影響。本文所做研究對在船舶設計時需考慮液艙晃蕩的影響具有一定的參考意義。