軌道交通網絡有效路徑搜索算法的改進及實現

,,

(蘇州大學軌道交通學院， 江蘇 蘇州 215131)

隨著我國城市軌道交通的不斷建設和發展，許多城市的軌道交通逐漸由單線運營向網絡化運營轉變。因此，城市軌道交通網絡中的每一對起訖站點之間可能存在多條合理的出行路徑。在無縫換乘模式下，通過AFC刷卡數據可以得到乘客具體的上下車站和時間信息，但卻無法直接獲得乘客在網絡中的具體走行路徑。把握乘客在軌道交通網絡中的出行路徑對于分析網絡客流規律和多家運營商背景下的票務清分來說具有重大的意義。

目前，在城市道路網絡中出行者選擇行為和路徑搜索算法方面，國內外專家學者取得了豐富的成果，提出了許多路徑搜索理論和算法[1-4]。Dial[1]認為當一條路徑所包含的所有路段都使出行者離起始節點越來越遠，離終點節點越來越近，則這條路徑是“有效”的，并提出一種有效路徑求解算法。Hoffman等[2]最早提出了K短路徑的算法，用以求出起終點間最短、次短和第K短路徑。Christopher和Brace[3]研究了K短路徑長度、不經過重復節點的K短路徑和帶單邊約束的最短路徑等問題。

但是與城市道路網絡相比，城市軌道交通網絡在節點性質、網絡構成、阻抗計算方法、影響因素等方面都具有不同的特性[5-7]。軌道交通網絡節點處存在節點阻抗(停車時間、換乘時間)，因此在實際應用中往往需要進行特殊的處理。林湛等[8]根據最短路徑費用定義OD之間的有效路徑集合，錢堃等[9]重點研究了換乘時間對乘客路徑選擇行為的影響，但都沒有對軌道交通網絡節點的具體處理方式進行闡述。四兵鋒等[10]在客流分配模型中將網絡節點阻抗合并到區間阻抗中，這樣處理雖然簡化了問題，但是可能造成搜索過程中路徑阻抗的計算偏差。周薇[11]在改進的Dial算法中將一個軌道交通車站表示成兩個節點，郭彥云[12]在對軌道交通網絡拓撲關系建模中同樣分拆了網絡節點，這樣處理有效地體現了節點阻抗，但是這種處理方式導致的有效路徑中可能存在冗余路段的問題卻沒有被提及。

基于上述分析，結合城市軌道交通自身特性，給出有效路徑中冗余路段的定義并提出增加冗余路段判定步驟的改進的有效路徑搜索算法，期望以此為基礎建立一個完整的軌道交通網絡客流路徑分析系統。

1 網絡節點及有效路徑定義

1.1 網絡節點處理

城市軌道交通網絡主要由區間和車站兩個部分組成，除了軌道交通區間有運行時間阻抗，軌道交通車站也存在停車時間阻抗，因此軌道交通網絡每個節點都存在節點阻抗。為了表示車站的停站時間，將每個軌道交通普通車站分拆表示為停車節點和出發節點，其間增加停車弧表示停車時間。

除固定的區間運行時間、停車時間之外，換乘步行時間和換乘等待時間也是軌道交通網絡阻抗的重要組成部分。對于軌道交通換乘站而言，節點阻抗存在兩種情況：一方面，如果乘客在換乘站不需要換乘，則只經歷停車時間，可看作普通車站，通過停車弧對其進行表示；另一方面，如果乘客在換乘站進行了換乘，則存在換乘時間，需要引入換乘弧對其進行描述。處理后的整個城市軌道交通網絡可以用“帶權有向圖”來描述。圖1和圖2分別表示普通車站和換乘車站的網絡節點示意圖。

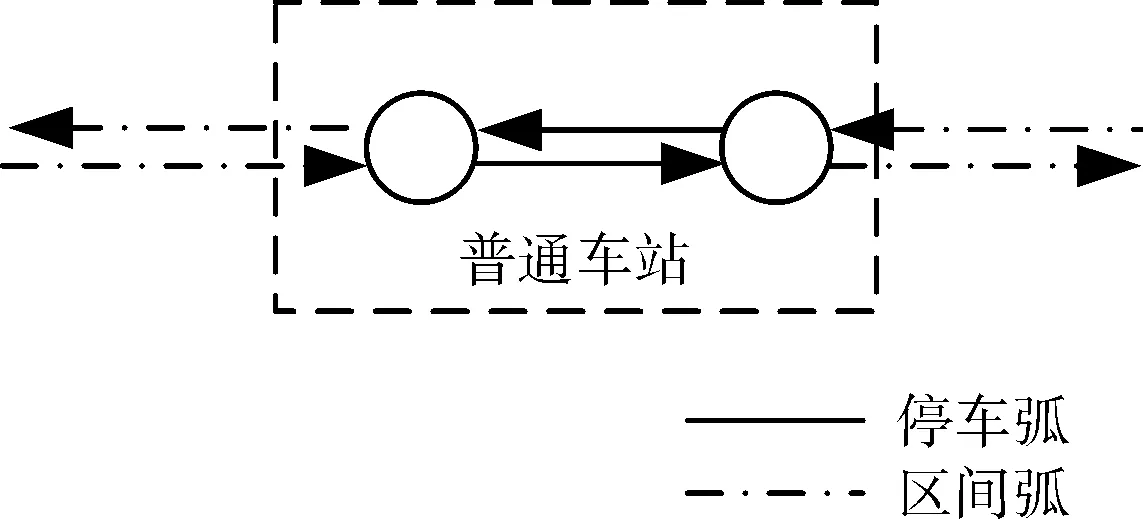
圖1 普通車站停車弧示意圖

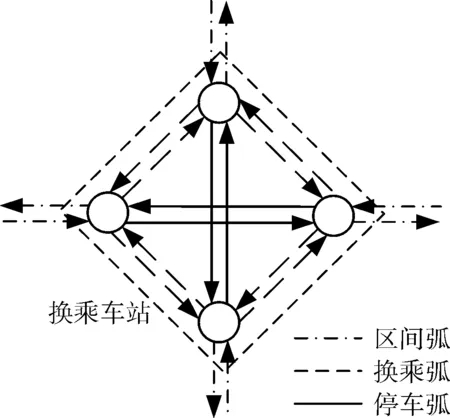
圖2 換乘車站換乘弧示意圖

1.2 有效路徑判定規則

在一次出行中，軌道交通乘客總是希望選擇出行費用(時間、票價等)最少的路徑，當起訖站點間有多條路徑可選時，乘客不會考慮全部的路徑，而是將其中幾條作為備選方案，那些被大多數乘客所考慮的費用相近的路徑便稱為“有效路徑”。

常用的有效路徑判定規則采用“相對值”法[13-15]，同時考慮到換乘次數的增加也會降低乘客的舒適性，因此在有效路徑的判定規則中增加換乘次數的限制。

定義1 當OD對(r,s)間的路徑k滿足以下3個條件，則稱其為有效路徑。

1)路徑k中不存在環路，即不重復經過同一個節點。

2)路徑k的阻抗小于等于最短路徑阻抗的1+Hrs倍，即：

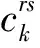
(1)

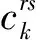
3)路徑k的換乘次數小于等于網絡最大換乘次數限制，即

Tk≤Tmax

(2)

式中：Tk為路徑k的換乘次數；Tmax為網絡最大換乘次數限制。

2 冗余路段定義及判定

2.1 路徑冗余路段定義

由于軌道交通車站節點的特殊處理，在實際操作過程中，通過未改進的有效路徑算法搜索到的僅僅滿足1.2中有效路徑判定規則的部分路徑中還包含了不符合換乘邏輯的路段。為了說明上述路段的特征，圖3為某個換乘車站網絡節點的示意圖，虛線框線內的節點歸屬于同一個車站，其中節點18、19、74、75為換乘車站節點，其余為普通車站節點。

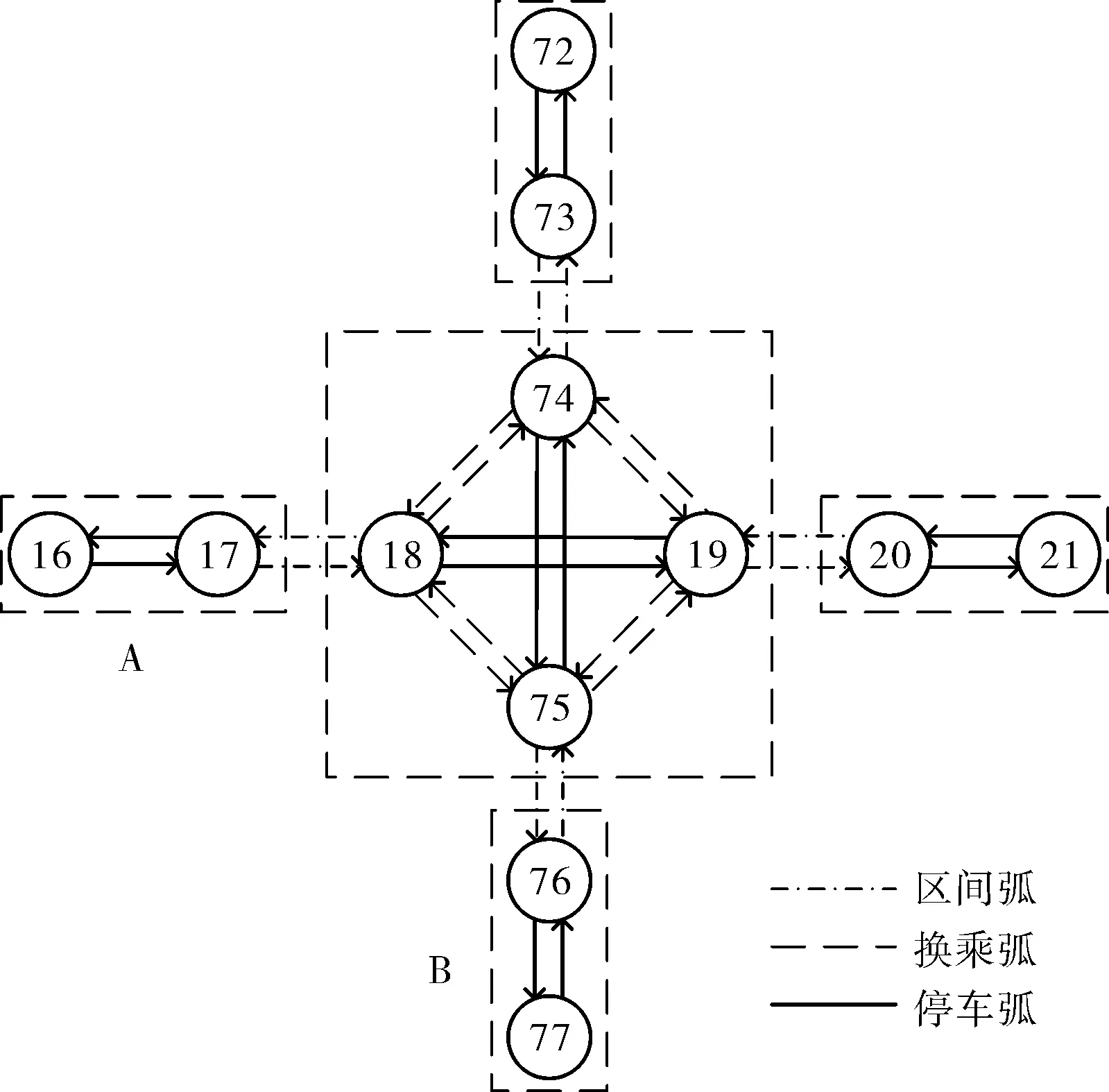
圖3 換乘車站網絡節點示意圖

假如某位乘客從車站A上車，在車站B下車，其間經過了兩段區間運行時間和一段換乘時間，可以看出，符合該乘客正確換乘邏輯的路徑應該是17-18-75-76。通過未改進的算法搜索到的相同起終點的路徑有17-18-74-75-76、17-18-19-75-76和17-18-74-19-75-76。這些路徑中均包含了不符合邏輯的停車時間和換乘時間，相應的18-74-75、18-19-75、18-74-19-75均可判定為冗余路段。結合以上分析，給出冗余路段的定義。

定義2 當有效路徑的路段兩端節點為換乘車站節點，且在路徑中體現為冗余停車時間或冗余換乘時間，則稱該路段為冗余路段。

2.2 路徑冗余路段判定

通過分析可以發現，不包含冗余路段的有效路徑中，路徑經過某換乘車站或在某換乘車站進行換乘則有且只有兩個換乘車站節點。因此，路徑中冗余路段的判斷邏輯為：如果有效路徑中有連續3個或3個以上換乘車站節點，則該路徑包含冗余路段。

為了篩選出包含冗余路段的有效路徑，設立變量transfer記錄網絡中某節點是否為換乘車站節點，具體定義為：

(3)

在此基礎上，根據每個節點的換乘節點變量transfer，搜索到的每條路徑便有1個對應的相同長度的換乘節點序列。遍歷路徑換乘節點序列的子序列，如果子序列集合中包含“1-1-1”或者“1-1-1-1”的元素，則說明該路徑中包含冗余路段，需要剔除。基于上述分析，以從節點17到節點76為例的路徑換乘節點序列和冗余路段判定見表1。

表1 路徑換乘節點序列和冗余路段判定示例

3 改進的有效路徑搜索算法

在充分考慮各種路徑搜索算法優缺點的情況下，采用深度優先遍歷算法來實現有效路徑搜索過程。

深度優先遍歷的思想是：假設初始狀態圖中所有頂點均未被訪問，從某個頂點v出發，首先訪問該頂點，然后依次從它的各個未被訪問的鄰接點出發深度優先搜索遍歷圖，直至圖中所有和v有路徑相通的頂點都被訪問到。若此時尚有其他頂點未被訪問到，則另選一個未被訪問的頂點作起始點，重復上述過程，直至圖中所有頂點都被訪問到為止。

在上述深度優先遍歷搜索算法中增加冗余路段判定步驟(Step 4)后，改進的有效路徑搜索算法具體步驟如下：

Step 0：初始化。給相關變量賦初值，輸入鄰接矩陣，設定參數。

Step 1：利用Dijkstra算法計算最短路徑阻抗，設根節點v為當前節點。

Step 2：從當前節點i出發，遍歷與節點i相鄰的節點，例如節點j，如果從根節點v出發沿著該路徑的阻抗小于或等于設定閾值并且滿足換乘限制條件，則令節點j為當前點，轉下一步，否則轉Step 6。

Step 3：判斷節點j是否為終節點，如果不是則轉入Step 2，否則進行下一步。

Step 4：判斷該路徑是否包含冗余路段，如果是則忽略該路徑并轉入Step 2，否則進行下一步。

Step 5：搜索前驅節點序列并輸出路徑。

Step 6：退回上一層，若未退回到根節點則轉入Step 2。

4 案例分析

為了檢驗改進的有效路徑搜索算法的可行性及有效性，利用某市軌道交通網絡進行案例分析。該市軌道交通網絡由1號線、2號線、3號線和4號線組成，共有5座換乘車站，網絡示意圖如圖4所示。

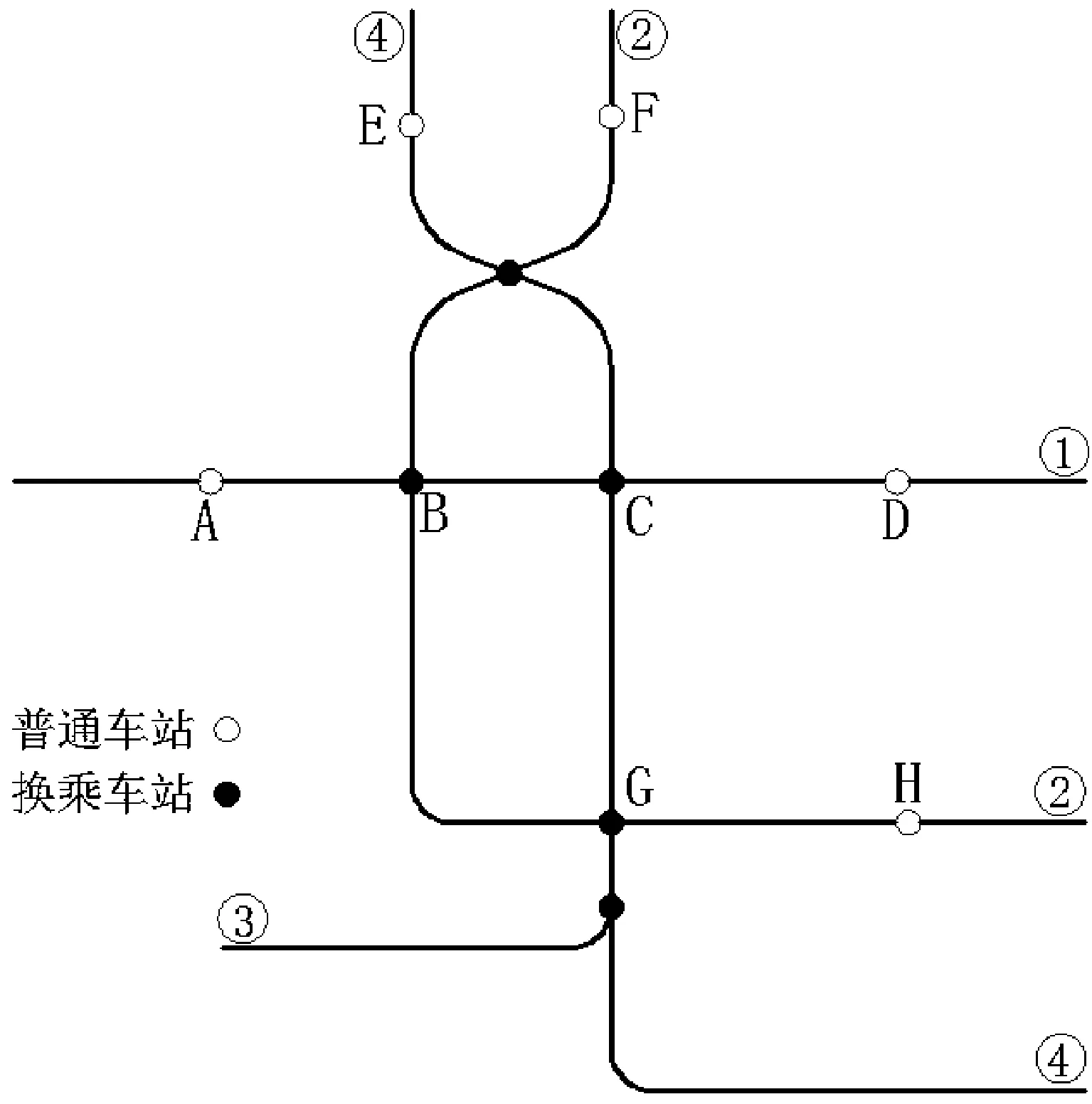
圖4 軌道交通網絡示意圖

4.1 網絡參數取值

網絡中停車時間、區間運行時間、換乘步行時間參數均為多次實測數據的平均值，換乘等待時間取各條線路平峰行車間隔的一半，網絡最大換乘次數限制取2。

除此之外，定義1中的路徑伸展系數是有效路徑判定條件中的重要參數。如果路徑伸展系數取值過大，路徑阻抗過大甚至存在繞行情況的路徑就被納入到有效路徑中；相反，如果取值過小，則會遺漏部分有效路徑。因此，路徑伸展系數的取值應根據具體的網絡形式確定，通過式(4)計算網絡主要換乘方向起訖點間最大合理路徑的伸展系數，具體計算結果見表2。

定義3 當一條路徑不經過背離起訖點方向的換乘站進行換乘，且在所有滿足條件的路徑中阻抗最大，則稱該路徑為最大合理路徑。

如從A站到E站，經過G站換乘的路徑則是不合理的路徑。

(4)

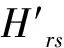
可以看出，除D—E起訖點外，其他起訖點間最大合理路徑的阻抗與最短路徑阻抗十分接近。對于該市軌道交通網絡來說，路徑伸展系數取0.3即可滿足要求。

表2 主要起訖點間最大合理路徑伸展系數

4.2 有效路徑搜索結果

利用Python程序語言編寫改進后的搜索算法，并對A站與H站之間的有效路徑進行搜索。如果采用未改進的算法，則程序輸出結果顯示有20條，但是經過人工辨識，其中有18條都包含冗余路段。這正是由于網絡節點的特殊處理方式以及多個換乘站間冗余路段的乘積效應導致的有效路徑數量與實際數量產生明顯偏差。同時，由于冗余路段的存在，輸出的路徑阻抗也與真實的路徑阻抗存在偏差。

現采用改進后的算法對A站與H站之間的有效路徑進行搜索，共得到2條有效路徑，結果表明改進后的算法能有效剔除包含冗余路段的路徑，具體路徑信息如表3所示。程序輸出的有效路徑信息符合乘客實際的換乘行為，并且保證了有效路徑信息的正確性。

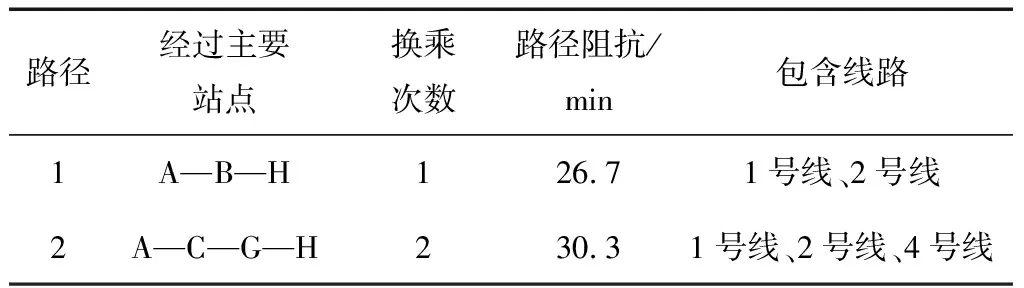
表3 A站-H站間有效路徑信息

5 結束語

基于對軌道交通網絡節點處理方式和有效路徑搜索算法進行研究，對于在實際操作過程中發現的通過未改進算法搜索有效路徑仍可能包含冗余路段的問題，給出了一種解決方法。

歸因于軌道交通網絡車站節點的特殊處理，通過深度優先算法搜索到的有效路徑中可能包含冗余的停車時間或換乘時間。通過實例分析冗余路段的特征并給出冗余路段的定義。在深度優先搜索算法中增加了冗余路段判定步驟，具體為分析路徑換乘節點序列的子序列集合中是否存在特定元素，進而改進了算法。實例分析中算法改進前后的搜索結果表明改進后的算法能夠正確地篩選出軌道交通網絡有效路徑，得到完整的有效路徑信息。研究成果為建立完整的城市軌道交通網絡客流路徑分析系統奠定了基礎。