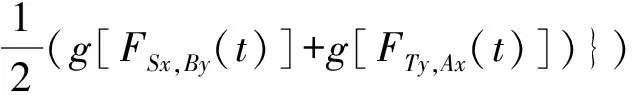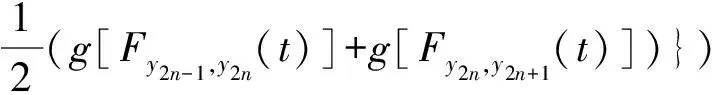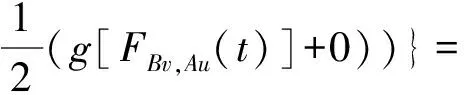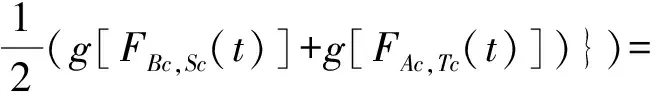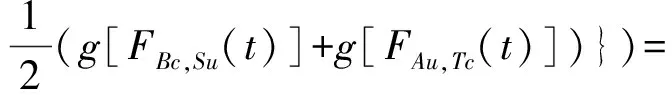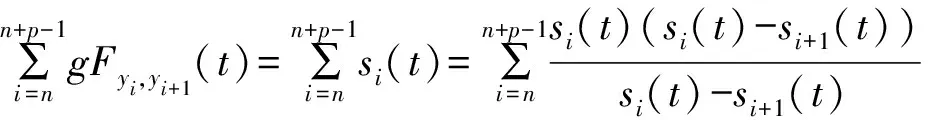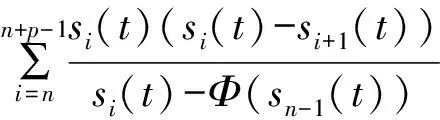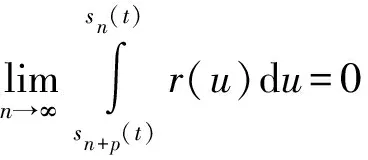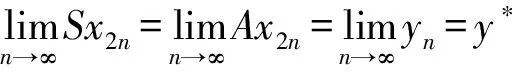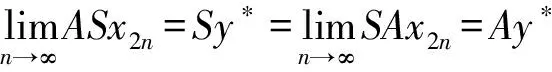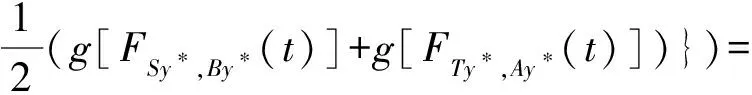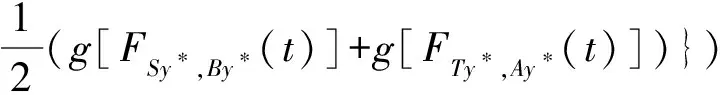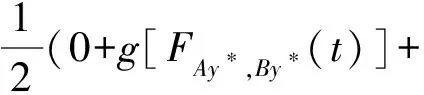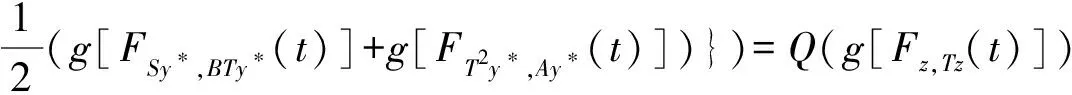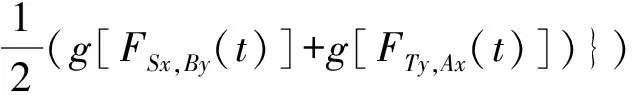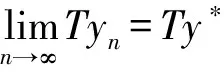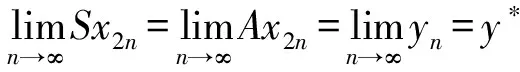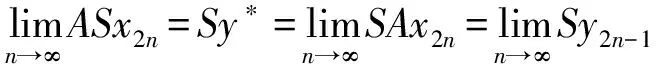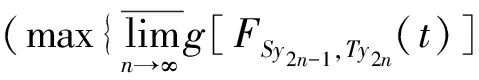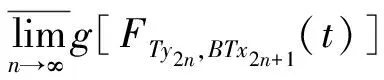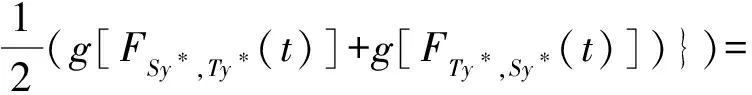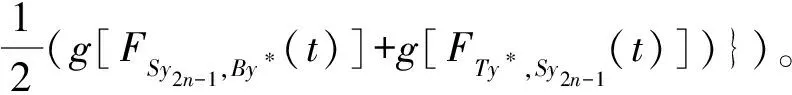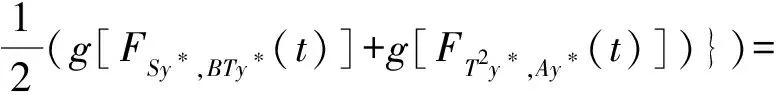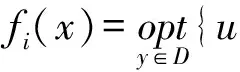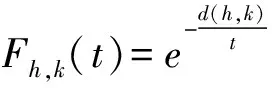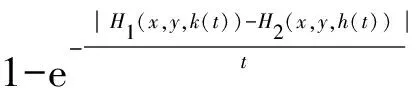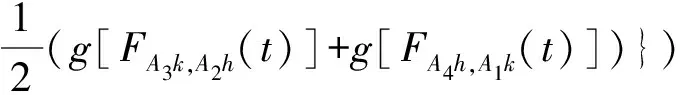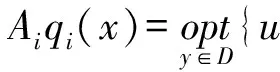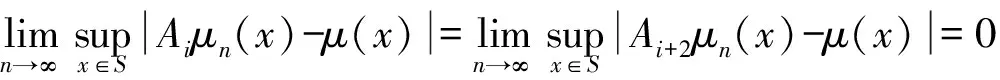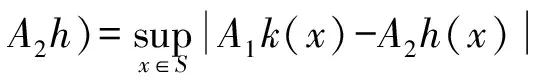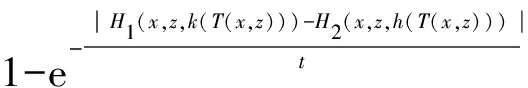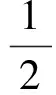非阿基米德Menger概率度量空間中Altman型映象公共不動點定理及其在動態規劃中的應用
, ,
(渤海大學數理學院, 遼寧 錦州 121013)
1 引言與預備知識
Istratescu等[1]引入并研究了非阿基米德Menger概率空間和一些拓補性質。隨后許多人在非阿基米德Menger概率空間建立了一些不動點存在性定理[2-10]。 另一方面, Altman[11]在完備度量空間中證明了一個映象f的不動點定理, 而這一映象f滿足d(fx,fy)≤Φ(d(x,y)), 其中Φ∈Φ1(Φ1的定義見下面)。 此后文獻[12]推廣了文獻[11]中的結果。這里一個問題自然出現: 可否在非阿基米德概率度量空間(X,F,Δ)中建立Altman型映象的不動點定理。 由于(C)g型的非阿基米德 Menger概率度量空間(X,F,Δ)中gF滿足三角不等式,即?x,y,z∈X,?t≥0, 有gFx,y(t)≤gFx,z(t)+gFz,y(t), 因此在(C)g型的非阿基米德Menger概率度量空間(X,F,Δ)中討論Altman型映象不動點的存在性成為可能。近些年來, 文獻[13-22]研究了若干非線性映象類不動點的存在性與迭代逼近, 這其中文獻[13]在模糊度量空間中建立了壓縮型映象不動點定理并討論了一類泛函方程解的存在性與唯一性。受上述工作啟發, 本文在非阿基米德概率度量空間中證明 Altman型映象的公共不動點的存在性和唯一性定理, 作為應用我們還討論了起源于動態規劃的一類泛函方程組解的存在與唯一性。
定義Φ1={Φ:Φ:[0,∞)→[0,∞) 是單調遞增滿足(c1),(c2)和(c3)}, 其中條件(c1),(c2),(c3)如下:
(c1) 0<Φ(u)
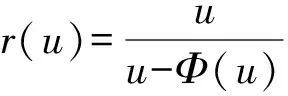
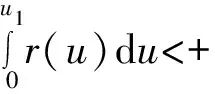
注1 如果Φ∈Φ1, 則Φ(0)=0且Φ(u)=u?u=0。
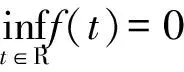
定義2[7]設X是非空集,D為全體分布函數,F:X×X→D,稱(X,F)為非阿基米德概率度量空間, 若滿足下面條件:(對x,y∈X,分布函數F(x,y)記為Fx,y)
1) 對?t>0,Fx,y(t)=1當且僅當x=y;
2)Fx,y=Fy,x,?x,y∈X;
3)Fx,y(0)=0,?x,y∈X;
4) 若Fx,y(t)=1,Fy,z(s)=1,則Fx,z(max{t,s})=1,?x,y,z∈X。
定義3[10]映象Δ:[0,1]×[0,1]→[0,1]稱為三角范數, 如果滿足以下條件
(i) ?a∈[0,1],Δ(a,1)=a,
(ii) ?a,b∈[0,1],Δ(a,b)=Δ(b,a),
(iii) ?a,b,c,d∈[0,1],若a≥b,c (iv) ?a,b,c∈[0,1],Δ(a,Δ(b,c))=Δ(Δ(a,b),c)。 定義4[7]三元組 (X,F,Δ) 稱為非阿基米德Menger概率度量空間, 若(X,F) 是一非阿基米德概率度量空間,Δ是滿足下列條件的Δ-范數。 5)Fx,z(max{t1,t2})≥Δ(Fx,y(t1),Fy,z(t2)),?t1,t2∈[0,∞),?x,y,z∈X。 設Ω={gg:[0,1]→[0,∞)連續,嚴格遞減,g(1)=0,g(0)<+∞}。 定義5[7]非阿基米德 Menger概率度量空間 (X,F,Δ) 稱為(C)g型的, 如果存在g∈Ω,使得?x,y,z∈X,?t≥0, 有gFx,y(t)≤gFx,z(t)+gFz,y(t)。 定義6[7]非阿基米德Menger概率度量空間(X,F,Δ)稱為(D)g型的, 如果存在g∈Ω,使得?s,t∈[0,1], 有g(Δ(s,t))≤g(s)+g(t)。 定義7[10]設(X,F,Δ)是(C)g型非阿基米德Menger概率度量空間, (X,F,Δ)中序列{xn}收斂于x當且僅當對?ε>0,λ>0, 存在N(ε,λ)∈N(正整數集), 使得n≥N,有gFxn,x(ε) 定義8[10]設(X,F,Δ)是(C)g型非阿基米德Menger概率度量空間,(X,F,Δ)中序列{xn}稱為Cauchy序列當且僅當對?ε>0,λ>0, 存在N(ε,λ)∈N(正整數集), 使得?n≥N,?p≥1,有gFxn,xn+p(ε) 定義9 設(X,F,Δ)是(C)g型非阿基米德Menger概率度量空間, 映象S,A:X→X稱為弱交換的, 如果?x∈X,?t>0, 有gFASx,SAx(t)≤gFSx,Ax(t)。 顯然可換映象一定是相容映象, 但反之不真。 引理1 設(X,F,Δ)是(C)g型非阿基米德Menger概率度量空間,S,A:X→X是相容映象, 如果Az=Sz,z∈X, 則ASz=SAz。 定理1 設(X,F,Δ)是完備的(C)g型非阿基米德Menger概率度量空間,(S,A),(T,B)是X→X的相容映象對,S,T,A,B連續,AX?TX,BX?SX, 使得?x,y∈X,?t>0, 有 (1) 其中Φ∈Φ1,則S,T,A,B在X上有唯一的公共不動點。 證明任取x0∈X, 作序列y2n=Ax2n=Tx2n+1,y2n+1=Bx2n+1=Sx2n+2(n=0,1,2,…), 對?t>0, 由式(1)有 g[Fy2n,y2n+1(t)]=g[FAx2n,Bx2n+1(t)]≤Φ(max{g[Fy2n-1,y2n(t)],g[Fy2n-1,y2n(t)], (2) 如果存在t0>0,使得g[Fy2n-1,y2n(t0)] g[Fy2n,y2n+1(t0)]≤Φ(g[Fy2n,y2n+1(t0)]) 矛盾。故對?t>0,有g[Fy2n-1,y2n(t)]≥g[Fy2n,y2n+1(t)], 從而由式(2)對?t>0,有 g[Fy2n,y2n+1(t)]≤Φ(g[Fy2n-1,y2n(t)])。 同理可證對?t>0,有 g[Fy2n-,y2n(t)]≤Φ(g[Fy2n-2,y2n-1(t)])。 于是?n≥1,?t>0, 有g[Fyn,yn+1(t)]≤Φ(g[Fyn-1,yn(t)])。 令sn(t)=gFyn,yn+1(t)。如果對某個n, 有s2n-1(t)=gFy2n-1,y2n(t)=0,?t>0, 則 y2n-1=y2n, 進而Sx2n=Ax2n=u, 由(S,A)是相容映象有Su=Au,由AX?TX, 故存在v,使Tv=Au, 從而由式(1)和(c1)有 g[FAu,Bv(t)]≤Φ(max{g[FSu,Tv(t)],g[FAu,Su(t)], Φ(g[FBv,Au(t)]) 所以Bv=Au,于是Su=Au=Bv=Tv=c, 進而由引理1有Sc=Ac,Bc=Tc。由式(1)和(c1)有 g[FAc,Bc(t)]≤Φ(max{g[FSc,Tc(t)],g[FAc,Sc(t)], Φ(g[FAc,Bc(t)]) 所以Sc=Tc=Bc=Ac。下面證c是S,T,A,B在X上公共不動點。由(1)和(c1)有 g[Fc,Bc(t)]=g[FAu,Bc(t)]≤Φ(max{g[FSu,Tc(t)],g[FAu,Su(t)],g[FBc,Tc(t)], g[Fc,Bc(t)]))=Φ(g[Fc,Bc(t)]) 表明c=Bc。 類似地如果對某個n,有s2n(t)=gFy2n,y2n+1(t)=0,?t>0, 則S,A,T,B也存在不動點。故若對某個n,有sn(t)=gFyn,yn+1(t)=0,?t>0, 則S,A,T,B存在不動點。 以下可設?n≥0,?t>0,sn(t)>0, 因Φ∈Φ1, 所以對?n≥0,t>0,有δn+1(t)≤Φ(δn(t))<δn(t)。 這蘊含對?t>0, {sn(t)}是關于n嚴格遞減的正數列,從而對?t>0, {sn(t)}收斂。 現證{yn}是X中的Cauchy列。事實上, ?t>0, ?n∈N(正整數集),?p≥1, 由條件(c1)和(c2)有 (3) 故對?t>0,由式(3)和T,S的連續性知 g[FBTx2n+1,Ty*(t)]≤g[FBTx2n+1,TBx2n+1(t)]+g[FTBx2n+1,Ty*(t)]→0(n→∞), g[FASx2n,Sy*(t)]≤g[FASx2n,SAx2n(t)]+g[FSAx2n,Sy*(t)]→0(n→∞)。 據此及A,B連續性有 于是?t>0, 由式(1)有 g[FAy*,By*(t)]≤Φ(max{g[FSy*,Ty*(t)],g[FSy*,Ay*(t)], Φ(max{g[FSy*,Ay*(t)]+g[FAy*,By*(t)]+g[FBy*,Ty*(t)], 0+g[FBy*,Ay*(t)])})=Φ(g[FAy*,By*(t)])。 因此Ay*=By*=Sy*=Ty*=z。下證z是S,T,A,B在X上的公共不動點。 事實上, 由于By*=Ty*=z, 且B,T是相容的, 故由引理1有BTy*=TBy*。又?t>0, 由式(1)有 g[Fz,Tz(t)]=g[FAy*,TBy*(t)]=g[FAy*,BTy*(t)]≤Q(max{g[FSy*,T2y*(t)],g[FSy*,Ay*(t)], 于是Tz=z, 從而Bz=BTy*=TBy*=Tz=z。同理可證Sz=z=Az, 因此z是S,T,A,B在X上的公共不動點。唯一性顯然。證畢。 如果我們用Φ的連續性代替映象A,B連續性, 則有下列結果。 定理2 設(X,F,Δ)是完備的(C)g型非阿基米德Menger概率度量空間,(S,A),(T,B)是X→X的相容映象對,S,T連續,AX?TX,BX?SX, 使得?x,y∈X,?t>0, 有 g[FAx,By(t)]≤Φ(max{g[FSx,Ty(t)],g[FSx,Ax(t)], (4) 其中Φ∈Φ1且上半連續,則S,T,A,B在X上有唯一的公共不動點。 證明任取x0∈X, 作序列y2n=Ax2n=Tx2n+1,y2n+1=Bx2n+1=Sx2n+2(n=0,1,2,…), (5) 故對?t>0,由式(5)和T,S的連續性知 g[FBTx2n+1,Ty*(t)]≤g[FBTx2n+1,TBx2n+1(t)]+g[FTBx2n+1,Ty*(t)]→0(n→∞), g[FASx2n,Sy*(t)]≤g[FASx2n,SAx2n(t)]+g[FSAx2n,Sy*(t)]→0(n→∞), 于是?t>0,由式(4)有 g[FASx2n,BTx2n+1(t)]≤Φ(max{g[FSy2n-1,Ty2n(t)],g[FSy2n-1,ASx2n(t)], 在上式中令n→∞時取極限, 得 從而?t>0,g[FSy*,Ty*(t)]=0,即Sy*=Ty*。又?t>0,由式(4)有 g[FASx2n,By*(t)]≤Φ(max{g[FSy2n-1,Ty*(t)],g[FSy2n-1,ASx2n(t)], 在上式中令n→∞時取極限, 得 g[FSy*,By*(t)]≤Φ(max{g[FSy*,Ty*(t)],g[FSy*,Sy*(t)], 從而?t>0,有g[FSy*,By*(t)]=0,即Sy*=By*。 同理可證Ty*=Ay*。因此Sy*=By*=Ty*=Ay*=z。 下證z是S,T,A,B的唯一公共不動點。 事實上, 由于By*=Ty*=z, 且B,T是相容的, 故由引理1有BTy*=TBy*。又?t>0,由式(4)有 g[Fz,Tz(t)]=g[FAy*,TBy*(t)]=g[FAy*,BTy*(t)]≤Φ(max{g[FSy*,T2y*(t)],g[FSy*,Ay*(t)], 因此Tz=z, 從而Bz=BTy*=TBy*=Tz=z。同理可證Sz=z=Az, 因此z是S,T,A,B在X上的公共不動點。唯一性顯然。證畢。 設R=(-∞,+∞),X和Y是實Banach空間,S?X為狀態空間,D?Y為決策空間,B(S)是S上有界實函數全體,x和y分別為狀態向量和決策向量,T為過程變換,f(x)為具有初始狀態x的最優返回。下面我們利用定理1, 討論下列起源于動態規劃的泛函方程的解的存在性和唯一性: (6) 其中:i=1,2,3,4,x∈S,opt=sup或opt=inf,u:S×D→R,T:S×D→S, 其中:d(h,k)=sup{h(x)-k(x):x∈S}。對?a,b∈[0,1], 取Δ(a,b)=max{a+b-1,0}。則易知(B(S),F,Δ)是完備的(D)g型非阿基米德Menger概率度量空間, 進而由注2可知(B(S),F,Δ)也是完備的(C)g型非阿基米德Menger概率度量空間, 其中g:[0,1]→[0,∞),g(x)=1-x,?x∈[0,1]。 定理3 設 1)u,Hi(i=1,2,3,4)有界; 2) 對任意(x,ξ,y)∈S×S×D,k,h∈B(S)和t>0, 有 其中g:[0,1]→[0,∞),g(x)=1-x,?x∈[0,1],Φ∈Φ1, 3)A1(B(S))?A4(B(S)),A2(B(S))?A3(B(S)); 4) 對Ai(i=1,2,3,4), 滿足任意的{γn}n≥1?B(S),γ∈B(S),有 5) 對任意的{μn}n≥1?B(S), 如果存在μ∈B(S),當 證明任意的k,h∈B(S),定義d(k,h)=sup{k(x)-h(x),x∈S},由條件1)可知,Ai:B(S)→B(S),i=1,2,3,4。由條件4)和條件5),A1,A2,A3,A4是連續的,并且A1與A3,A2與A4是相容的。若opt=sup,則由條件2)中Aiqi(x)的定義,對任意的k,h∈B(S),x∈S, 對任意的ε>0,存在y,z∈D, 有下列不等式成立: A1k(x) A1k(x)≥u(x,z)+H1(x,z,k(T(x,z))),A2h(x)≥u(x,y)+H2(x,y,h(T(x,y)))。 由上面不等式容易得到 A1k(x)-A2h(x) 和 A1k(x)-A2h(x)>H1(x,z,k(T(x,z)))-H2(x,z,h(T(x,z)))-ε 令ε→0,得 于是對?t>0,有 進而對?t>0,有 因此對?t>0, 由條件2)有 Φ(max{g[FA3k,A4h(t)],g[FA3k,A1k(t)],g[FA4h,A2h(t)], (7) 若opt=inf,則類似于上面證明過程可知式(7)成立。于是由定理1可知,A1,A2,A3,A4有唯一的公共不動點q∈B(S),即q為泛函方程組(6)的唯一公共解。證畢。
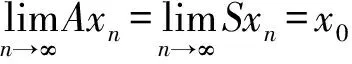
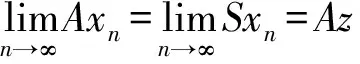
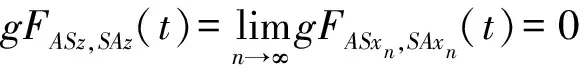
2 主要結果