一類食餌具有脈沖生育和Iv1ev型功能性反應的食餌-捕食者模型的動力學分析

梁桂珍，劉蒙蒙,2

（1.新鄉學院 數學與信息科學學院，河南 新鄉 453003；2.鄭州大學 數學與統計學院，河南 鄭州 453000）

以常微分方程為基礎發展起來的脈沖微分方程能反映物種瞬間的變化，能更加合理、形象地描述現實生活中很多生命現象和人類對生物種群的放養、收獲等行為。近年來，人們越來越多地將脈沖控制方法應用于種群系統持久性和穩定性方面的研究［1-4］。 陳蘭蓀等［5］研究了不同脈沖時刻的收獲捕食者和生育食餌，但沒有考慮功能性反應函數。人們在研究生物種群時常用Machaelis-Menten 型、Beddington-Deangelis型、Holling I型、Holling II型、Holling III型和Holling IV型功能性反應函數，而很少用到Ivlev型功能性反應函數。焦建軍等［6］研究了捕食者是脈沖投放捕食者，且具有脈沖擾動和Ivlev型功能性反應函數的捕食-食餌模型。陳蘭蓀［7］研究了具有生育脈沖效應的單種群模型。在本文中，我們在模型［8-9］的基礎上研究了一類帶有Ivlev型功能性反應函數的食餌具有生育脈沖效應和捕食者具有連續收獲的食餌-捕食者模型，建立了如下的捕食系統：

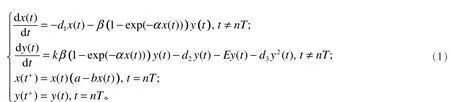
1 基本引理

引理 1［10］：設是系統（1）的解，且有則對所有的 t ≥0，均有 z (t)≥0。 若 z (0+)≥0,則當時，均有 z (t)≥0。

引理 2［11］：假設函數滿足不等式組

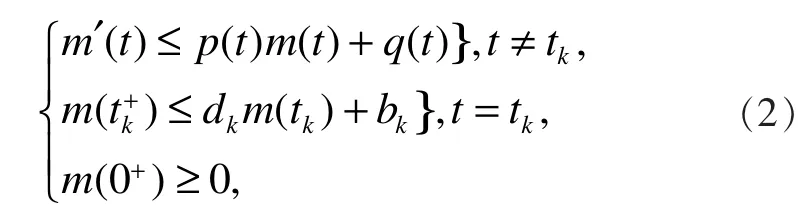
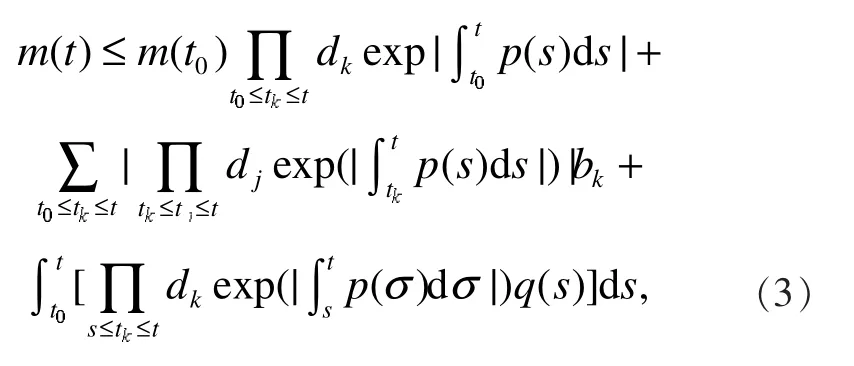
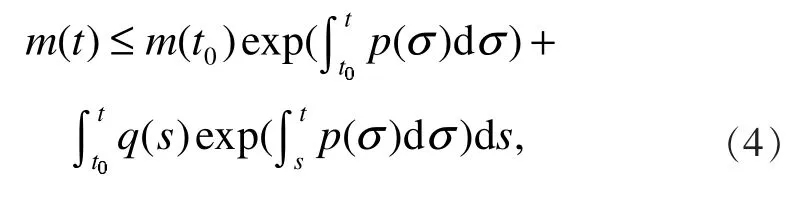
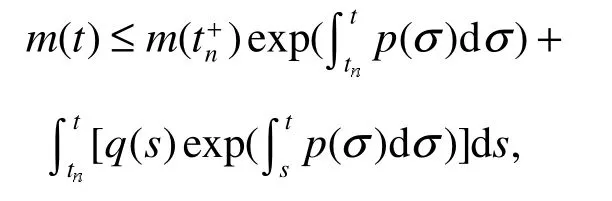
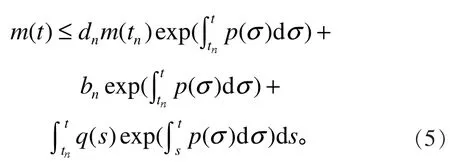
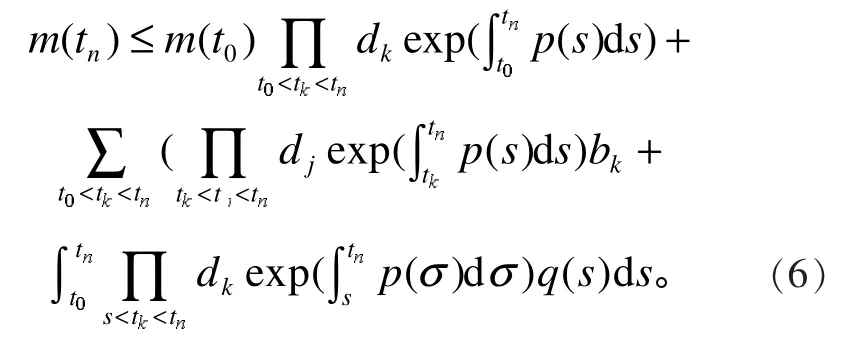
把式（6）代入式（5）可得

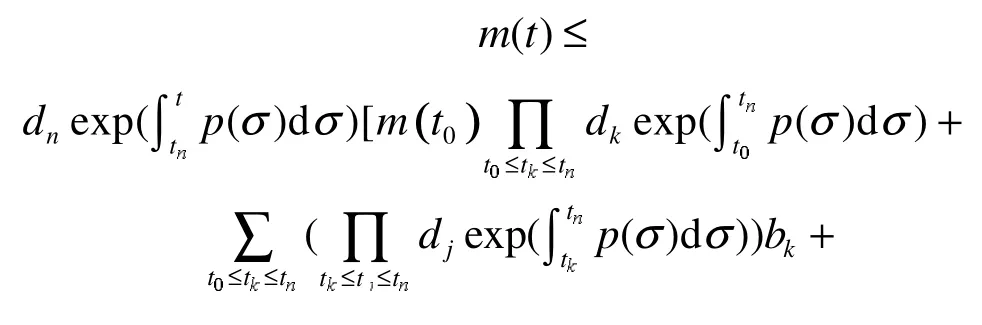
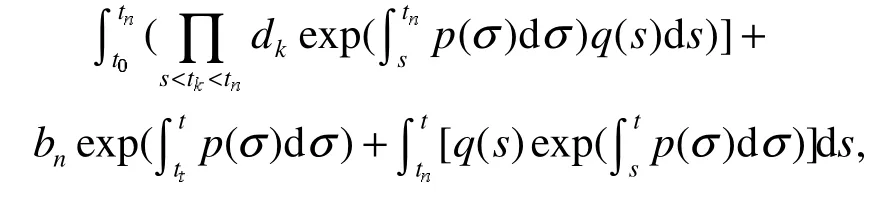
經過合并和化簡可得式（3）。

由引理2可知

引理 4［12］：脈沖系統

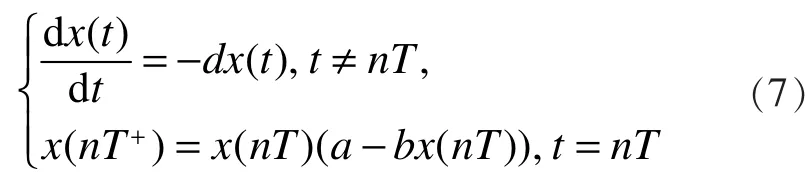
有一個全局漸近穩定的周期解

2 系統的持久性

考慮如下脈沖微分方程

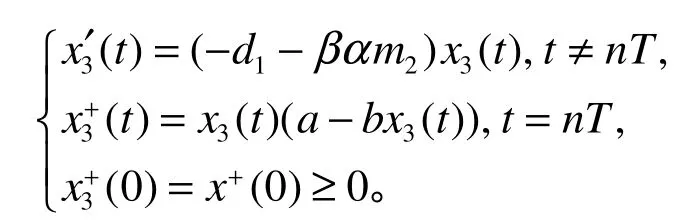
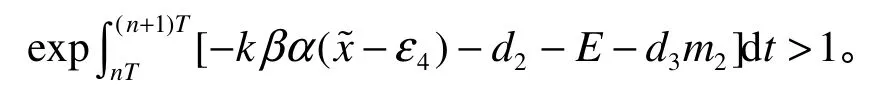
由系統（1）的第2個方程和第4個方程可得：

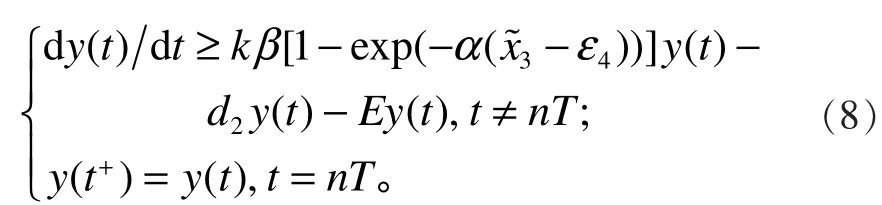
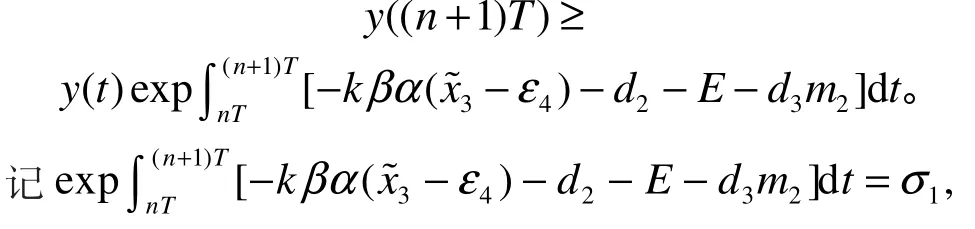
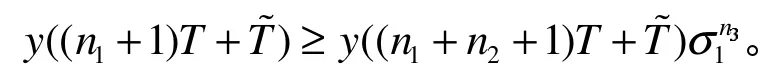
由系統（1）可得：

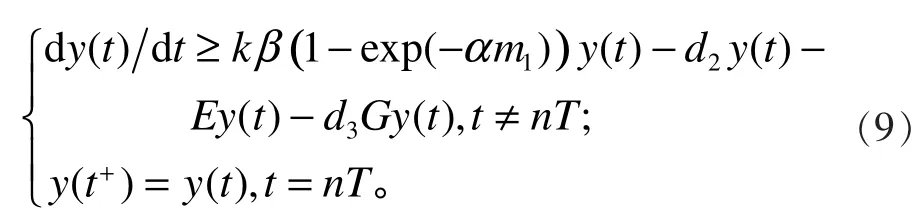
3 捕食者滅絕的全局漸近穩定性

由引理4可知，當捕食者滅絕時，系統（1）可簡化為系統（7）的形式，故存在相應的周期解為當時，有