基于AHP和BP神經網絡的翻轉課堂教學質量評價模型

喬維德（無錫開放大學 科研與質量控制處，江蘇 無錫 214011）

0 引 言

實施翻轉課堂是解決教師課堂講授能力差異的重要途徑，更是解決學生學習差異的有效途徑。與傳統課堂教學有所不同，翻轉課堂教學充分體現“以學為主、寓教于學”的現代教學理念，注重學生的學習過程管理與考核，強化學生的知識內化，滿足學生的個性自主學習需求，可極大地調動學生的學習主觀能動性和學習參與熱情，有利于建立良好、和諧、新型的師生和生生關系。目前，我國普通高校、職業院校等都在大力開展翻轉課堂教學改革活動，許多教師及相關學者也在進行翻轉課堂教學模式的應用實踐與研究，但針對翻轉課堂教學質量評價的研究成果并不多見。如構建翻轉課堂教學質量評價指標體系和評價系統[1-3]，采用模糊層次分析法評價翻轉課堂教學質量[4-5]等。現有翻轉課堂教學質量評價研究成果，一般僅停留于翻轉課堂教學質量評價指標體系的構建上，較少涉及指標體系中各指標權重分配，缺乏實證研究成果。翻轉課堂教學質量評價系統是一項系統工程，具有高度非線性、較強的時滯性和不確定性，如果仍單一采取傳統評價方法，難以對翻轉課堂教學質量作出公正、客觀、精準的評價。本文以翻轉課堂為研究對象，在分析影響翻轉課堂教學成效的關鍵要素前提下，運用層次分析法（AHP）構建翻轉課堂教學質量評價指標體系，確定各指標權重，建立BP神經網絡的翻轉課堂教學質量評價模型，采取改進粒子群算法優化網絡初始權值和閾值，利用改進BP算法、訓練BP神經網絡評價模型，以期用更科學、更有效、更客觀地評價翻轉課堂教學質量，為翻轉課堂的教學改革和教學質量提升提供參考依據。

1 翻轉課堂教學質量評價模型

基于AHP和BP神經網絡的翻轉課堂教學質量評價模型如圖1所示。首先在分析影響翻轉課堂教學質量因素的基礎上，運用AHP構建翻轉課堂教學質量評價指標體系，確定指標權重；然后建立BP神經網絡評價模型，利用改進粒子群算法優化BP神經網絡結構參數，并輸出最優的網絡初始權值與閾值，選取相關指標數據作為訓練樣本，由改進BP算法對BP神經網絡進行訓練；最后再利用樣本對已訓練好的BP神經網絡進行測試。其中運用AHP計算的綜合得分作為BP神經網絡的期望輸出，它與BP神經網絡實際輸出之間的誤差必須在規定的誤差精度范圍內。通過AHP與BP神經網絡的有機融合，可克服和避免在翻轉課堂教學質量評價過程中產生的主觀及人為因素，從而使翻轉課堂教學質量評價結果更公正、客觀、真實、科學。

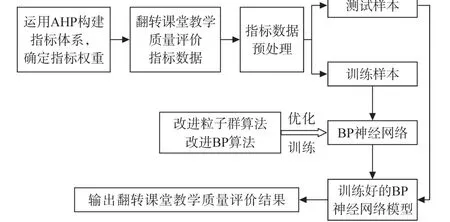
圖1 基于AHP和BP神經網絡的翻轉課堂教學質量評價模型

2 翻轉課堂教學質量評價指標體系的構建

2.1 建立遞階層次結構

翻轉課堂教學融合了傳統課堂教學要素及課堂翻轉變化的新要求和新特點，在實施過程中涉及的因素較多，且各因素之間又有關聯，因而運用AHP構建翻轉課堂教學質量評價指標體系時，要用系統工程的思維考慮問題，以客觀性、目的性、科學性及可比性、效益性為基本原則，注重評價指標的共性與個性、定性與定量的有機結合與有效轉化。翻轉課堂教學質量評價指標不僅需要具備普遍性，而且還需要呈現特殊性，評價時既要全面考慮翻轉課堂的各個環節，又要重點考核翻轉課堂的重點和關鍵環節，同時還要分析影響翻轉課堂教學質量的各因素之間存在的關聯度，從而保證評價結果更加客觀、合理、精準。影響翻轉課堂教學質量的各種外在和內在因素錯綜復雜，結合翻轉課堂教學模式的獨特性及對教師、學生的要求，對翻轉課堂教學進行質量評價。一是考慮課前教師準備與學生自主學習情況，如教學微視頻開發、學習任務書設計等；二是重點考查課堂學習與活動組織情況，如課中問題交流討論、課堂實踐活動操練、課堂學習成效等；三是注重學生的課后學習及師生的總結反思，如學生課后作業完成質量、學生課后拓展內容學習情況等。基于以上分析，在參考相關文獻、咨詢教育專家及征求師生代表意見基礎之上，構建了翻轉課堂教學質量評價指標體系（見表1）。該指標體系由目標層（M）、一級指標層（H）、二級指標層（W）、三級指標層（X）組成，其中，一級指標層有指標3項，二級指標層有指標9項，三級指標層有指標36項。

2.2 確定指標權重

采用1—9比率標度法建立翻轉課堂教學質量評價的權重判斷矩陣為：M—H，H1—W，H2—W，H3—W，W1—X，W2—X，W3—X，W4—X，W5—X，W6—X，W7—X，W8—X，W9—X（見表2～表14）。在權重判斷矩陣M—H中，“5”表示一級指標H2（課堂學習與活動組織）比一級指標H1（課前準備與學習）重要，“7”表示一級指標H2（課堂學習與活動組織）比H3（課后學習與反思）重要得多，而“1/5”則表示H1沒有H2重要，“1/7”表示H3沒有H2重要，因而將一級指標層中的課堂學習與活動組織、課前準備與學習、課后學習與反思所占的權重分別設定為0.48、0.35和0.17（見表2）。其它權重判斷矩陣以此類推。在計算以上各權重判斷矩陣特征向量且進行歸一化處理后，得到翻轉課堂教學質量評價指標合成權重（見表15），即三級指標層各指標相對目標層的綜合權重。

表1 翻轉課堂教學質量評價指標體系

表2 權重判斷矩陣M—H

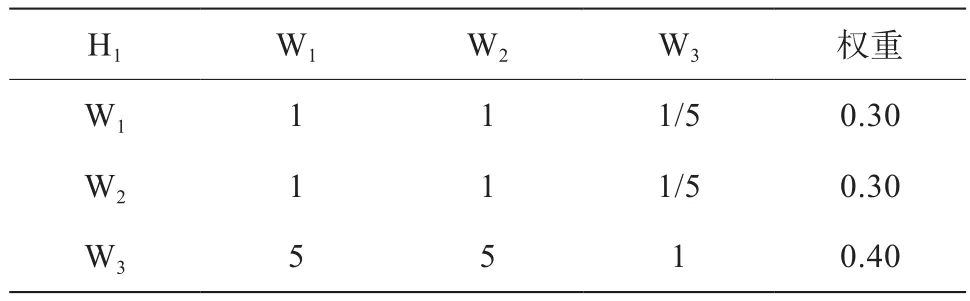
表3 權重判斷矩陣H1—W

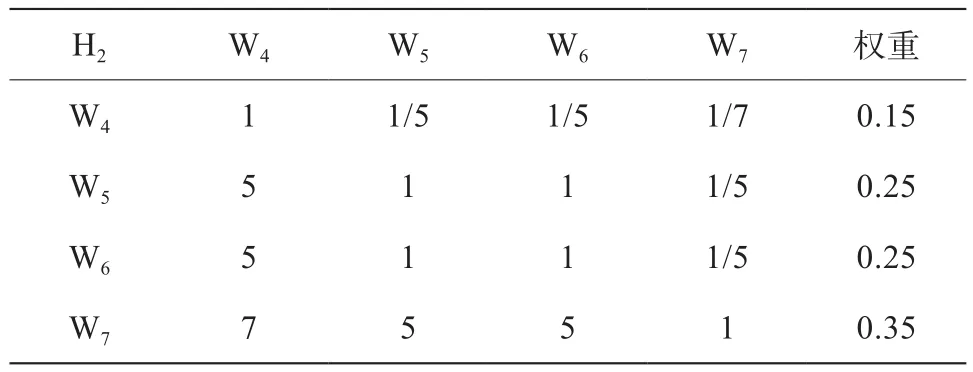
表4 權重判斷矩陣H2—W

表5 權重判斷矩陣H3—W

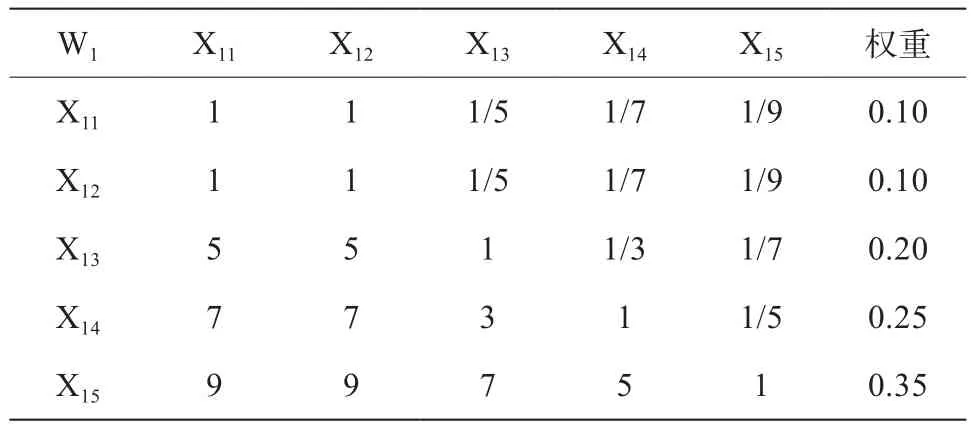
表6 權重判斷矩陣W1—X

表7 權重判斷矩陣W2—X

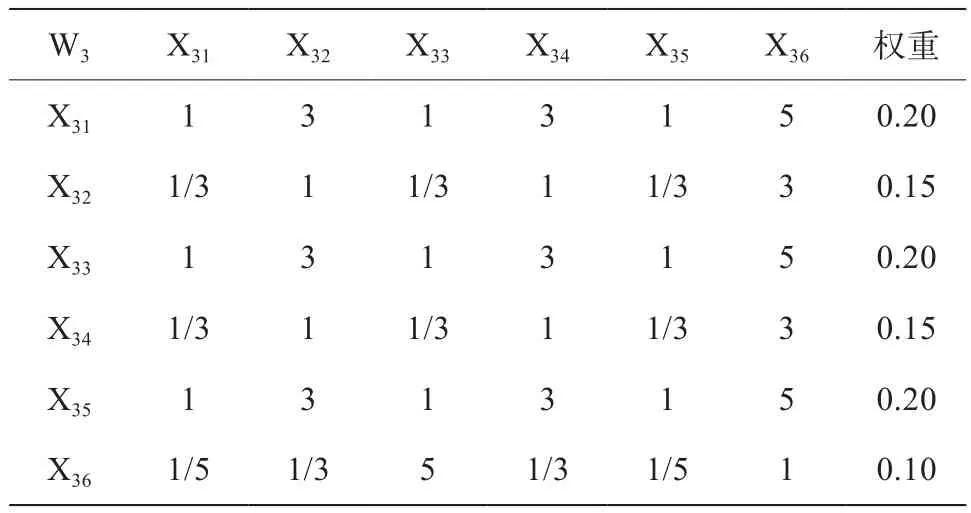
表8 權重判斷矩陣W3—X

表9 權重判斷矩陣W4—X

表10 權重判斷矩陣W5—X

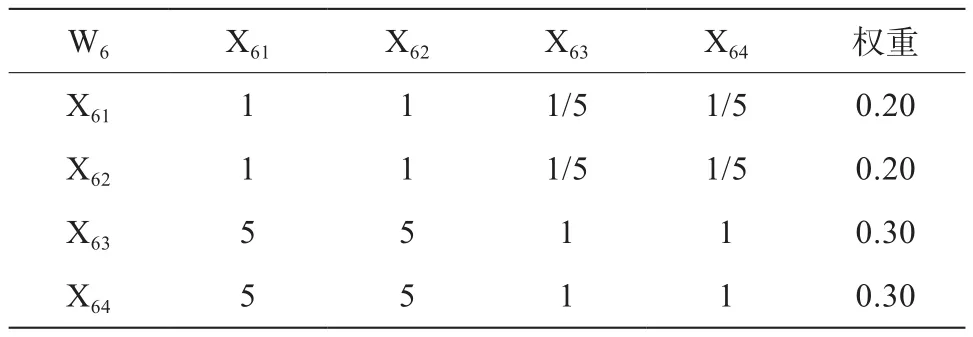
表11 權重判斷矩陣W6—X

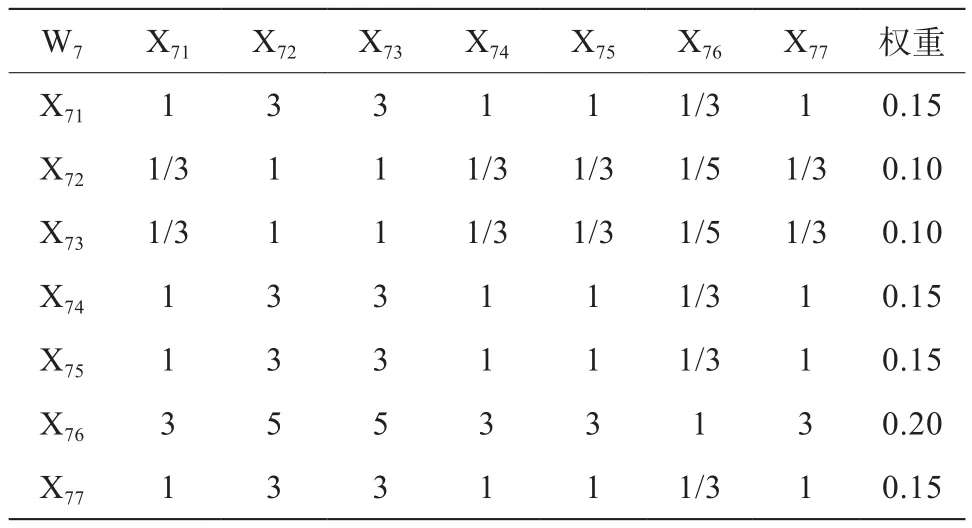
表12 權重判斷矩陣W7—X

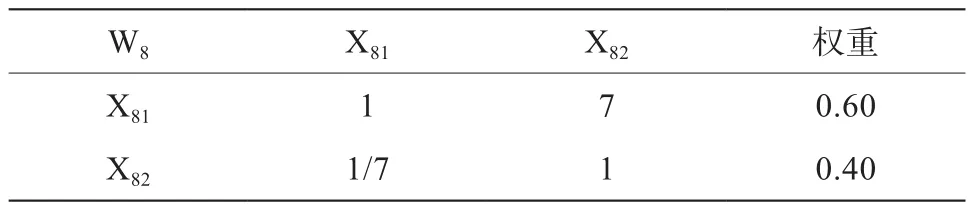
表13 權重判斷矩陣W8—X

表14 權重判斷矩陣W9—X

3 基于BP神經網絡的翻轉課堂教學質量評價

基于BP神經網絡的翻轉課堂教學質量評價模型[6-7]如圖2所示。

圖2 基于BP神經網絡的翻轉課堂教學質量評價模型

BP神經網絡需要經過不斷學習優化網絡結構參數，即輸入層與中間層之間的連接權值ωij，中間層與輸出層之間的連接權值Gki，以及中間層神經元節點閾值θi和輸出層神經元節點閾值θk，從而最終實現BP神經網絡實際輸出A與理想輸出B之間的偏差降至規定要求的誤差精度范圍內。鑒于BP神經網絡初始連接權值和閾值等結構參數的選擇對網絡輸出結果影響極大，針對傳統BP算法收斂速度慢，ωij,Gki,θi,θk等參數初始值較為敏感，易陷入局部極值等狀況，提出一種改進粒子群算法優化輸出BP神經網絡中ωij,Gki,θi,θk等最優初始連接權值和閾值，并通過改進BP算法對BP神經網絡加以學習訓練，直至BP神經網絡輸出誤差滿足要求為止。

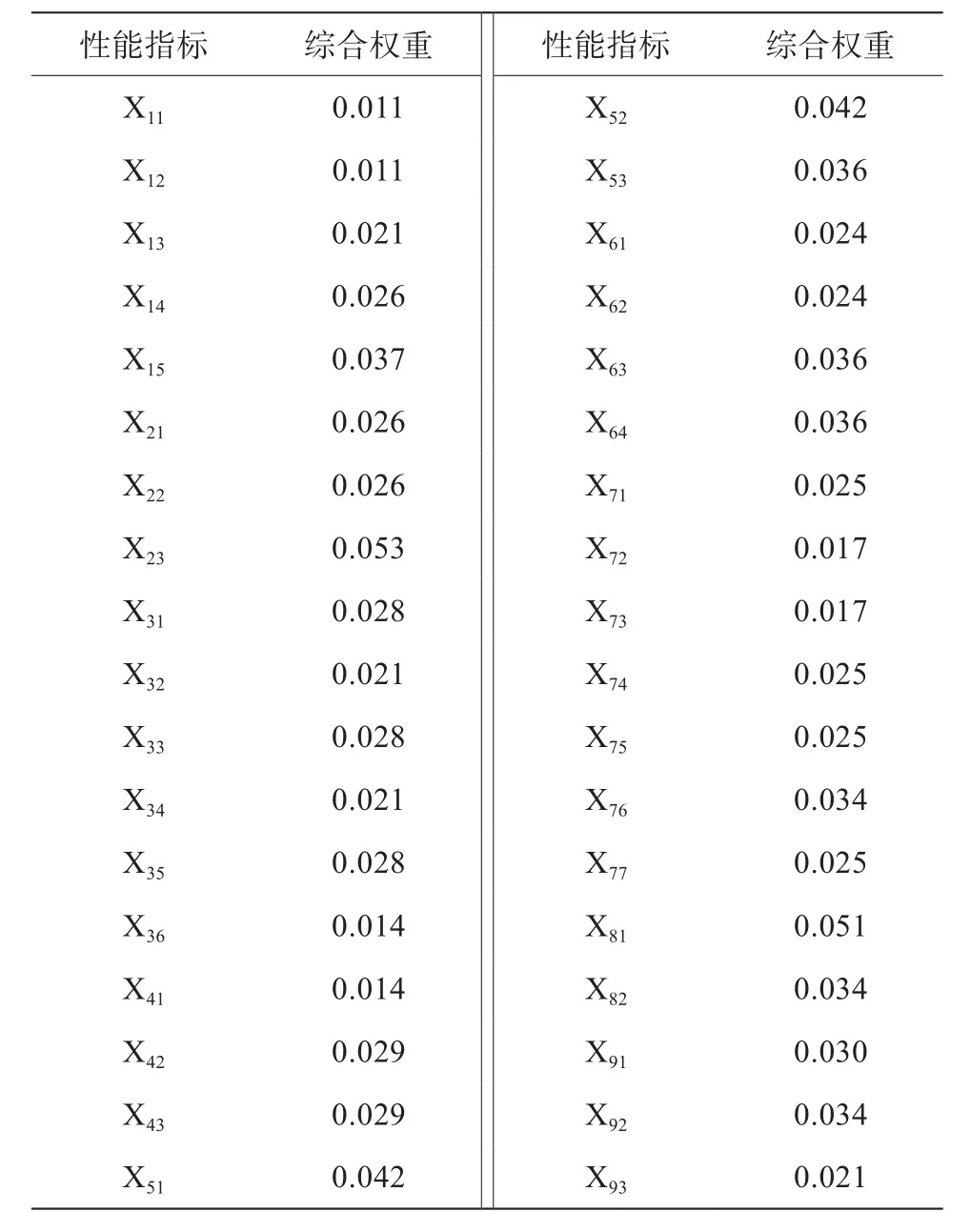
表15 翻轉課堂教學質量評價指標合成權重

為避免標準BP算法在學習訓練過程中陷入局部極小并可能出現振蕩現象，采取（1）、 （2）式所示的基于動量和自適應學習的改進BP算法。通過加入動量項可避免網絡學習訓練中產生振蕩；通過引入自適應學習因子調整學習率，可避免因過大或過小的學習率及過慢的收斂速度而導致系統產生振蕩乃至發散現象。

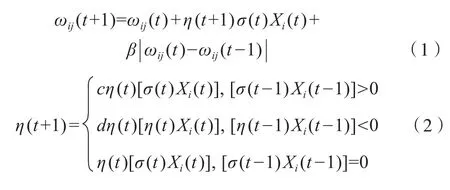
其中，β為動量因子?為加入的動量項；c,d為常數，且0＜c＜d；η為需要調整的學習率（學習步長）；σ為網絡神經元層之間的誤差；Xi為BP神經網絡層輸入信號。

標準粒子群（PSO）算法按（3）、 （4）式進行迭代計算，直至粒子搜索出最優位置。

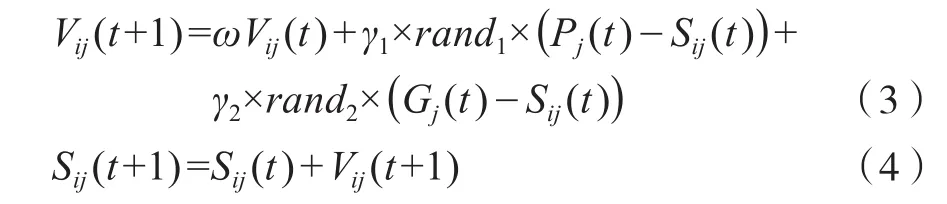
其中，t為尋優迭代次數；Sij（t）為粒子在t代時當前位置；Vij（t）為粒子在t代時速度；ω為粒子運動慣性權重，γ1,γ2為加速因子，分別修正朝著全局最優粒子和向個體最優粒子位置方向移動的最大步長，選取γ1=γ2=2；rand1,rand2為0～1隨機數。

為防止粒子群算法產生“早熟”現象，對慣性權重ω進行更新，讓其跟隨粒子群算法的迭代次數進行線性調節，即：

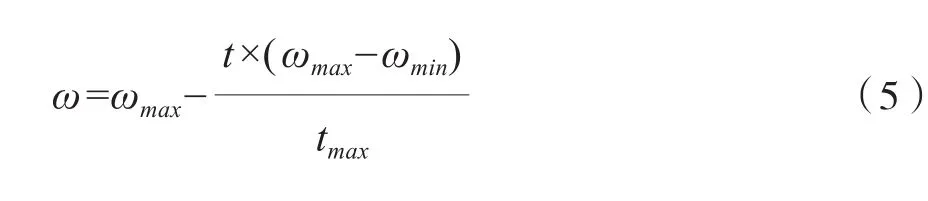
其中，ωmax為慣性權重最大值，ωmin為慣性權重最小值，t為當前更新迭代次數，tmax為最大更新迭代次數。

為擴展粒子群算法的搜索尋優空間，減少甚至消除粒子群在沒有完全搜索前陷入局部極值概率，當粒子每次迭代更新后對粒子按一定的變異概率g做重新初始化處理，即參照遺傳算法中種群變異思想，引入遺傳變異因子，從而實現粒子群算法的全局最優[8]。其操作方法為：

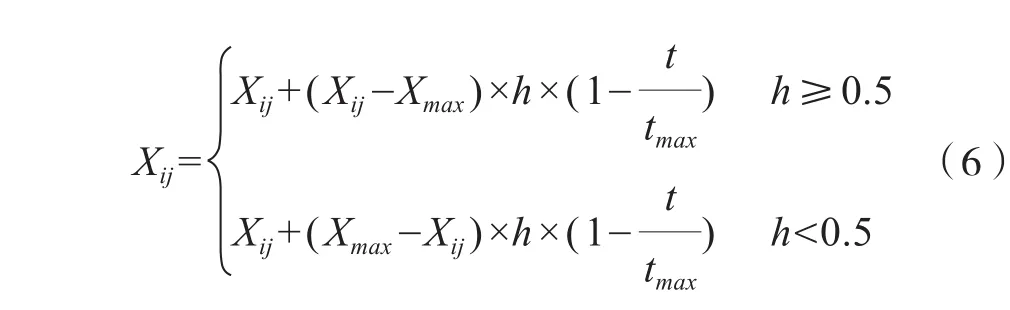
其中h為0～1之間的隨機值，由它決定粒子向著最大或最小位置方向變異。

由（7）式求得變異概率g：

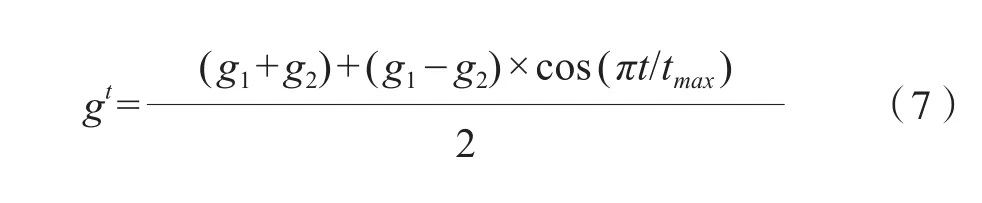
其中，g1,g2分別為變異概率的初始取值和最終取值，選取g1＜g2，以保證變異概率g根據余弦變化規律由小逐漸增大。

改進粒子群算法和BP算法優化訓練BP神經網絡流程[9]如圖3所示，其關鍵步驟如下：

（1）初始化算法參數，隨機初始化粒子群初始位置和初始速度，設定初始慣性權重ω和加速因子γ1,γ2，最大迭代次數tmax，確定BP算法的動量因子β，學習率η等。選定BP神經網絡輸入層、中間層及輸出層神經元個數各自為S1, S2, S3，即BP神經網絡的拓撲結構為S1—S2—S3，種群中的每個個體粒子對應于BP神經網絡各層所有神經元之間的連接權值和閾值，粒子維度表示為S1×S2+S2×S3+S2+S3，其中，連接權值個數為（S1×S2+S2×S3），閾值個數為（S2+S3）。

（2）選取翻轉課堂教學質量評價的樣本（含訓練、測試）數據，對樣本數據進行歸一化處理后，計算粒子群中每個粒子的適應度函數值。這里采用BP神經網絡輸出誤差E作為粒子群算法的適應度函數，則：

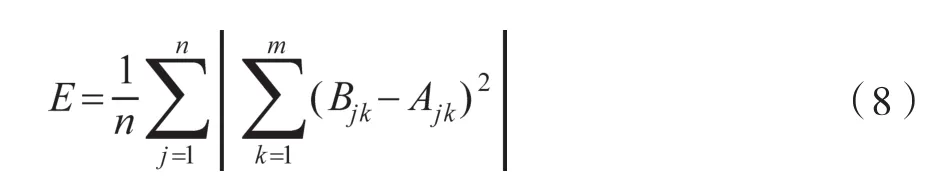
其中，Bjk為第j個訓練樣本在第k個輸出節點處的網絡期望輸出，Ajk為第j個訓練樣本在第k個網絡輸出神經元節點處的實際輸出，m為網絡輸出層神經元節點數（即m=S3），n為訓練樣本數。

（3）對于每個粒子的適應度值，如果其值好于全局最佳位置的粒子適應度函數值，則粒子位置為當前全局最佳位置。

（4）采用粒子群算法中（3）、 （4）、 （5）式分別更新粒子速度、位置。

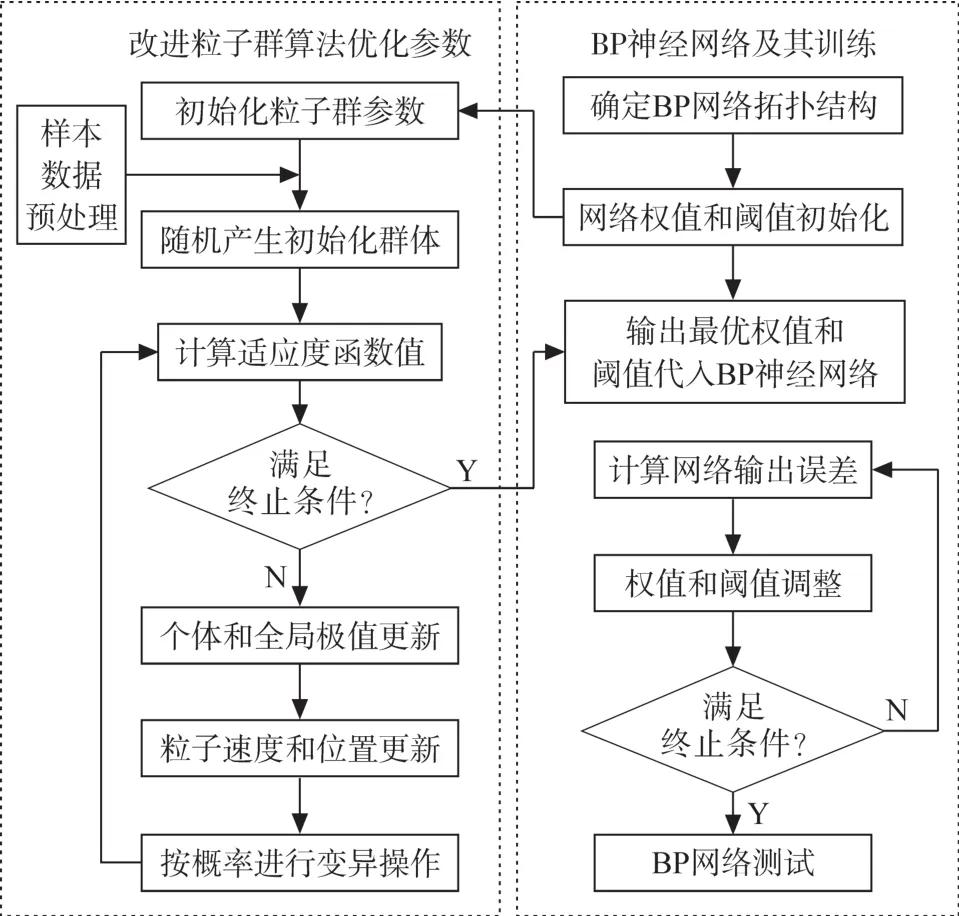
圖3 BP神經網絡優化訓練流程

（5）每次迭代更新粒子位置后，根據（6）、 （7）式對粒子以一定概率進行變異操作，完成重新初始化處理。

（6）重復執行步驟（2）～（5），當粒子適應度函數值達到規定精度和最大迭代次數時，改進粒子群算法搜索結束，輸出全局粒子最佳位置且映射為BP神經網絡的最優初始連接權值和閾值。

（7）采用改進BP算法，即按（1）、 （2）式對BP神經網絡加以訓練，不斷調整BP神經網絡的連接權值和閾值，直至滿足設定的最大訓練次數或網絡輸出達到最小誤差精度要求。

（8）將測試樣本輸入已訓練好的BP神經網絡，對翻轉課堂教學質量進行評價。

4 仿真實驗

4.1 指標數據預處理

翻轉課堂教學質量評價指標有36項，既有定性指標也有定量指標，但由于各指標量綱和單位有所不同，為便于對數據統一處理，應對定量指標數據進行歸一化處理，即：

其中，X *（k）為指標數據歸一化處理值，xkmax,xkmin分別為第k個指標數據的最大值和最小值。

翻轉課堂教學質量評價指標中絕大部分指標為定性指標，這些定性指標首先必須轉換為定量指標數據，即由教育領域的專家、評委按[0, 100]百分制打分考核，然后根據（9）式對定量指標數據進行歸一化處理，再將相關數據轉換為0～1區間范圍內的評價值。

4.2 BP神經網絡結構

（1）輸入層節點數。BP神經網絡輸入層節點數取決于翻轉課堂教學質量評價指標的個數，翻轉課堂教學質量評價指標36項分別對應BP神經網絡的36個輸入神經元，BP神經網絡輸入量為經過歸一化處理后的翻轉課堂教學質量評價指標數據值。

（2）中間層節點數。中間層神經元節點數由（10）式計算得出，即：

其中q取值為1～10之間的常數。通過多次實驗，確定中間層節點數為12。

（3）輸出層節點數。以翻轉課堂教學質量評價指標36項數據值作為BP神經網絡輸入信號，將翻轉課堂教學質量評價結果A作為BP神經網絡輸出。評價結果A根據評價分值高低順序共設定5個等次，分別為優秀[1～0.9]、良好（0.9～0.8]、中等（0.8～0.7]、合格（0.7～0.6]、不合格（0.6～0]，因而輸出層節點數有5個。

據此BP神經網絡拓撲結構設計為36—12—1，粒子維度（數）d=36×12+12×1+12+1=457，其中，包含網絡各層之間的連接權值數444個，閾值數13個。

4.3 訓練與測試樣本

從無錫、常州等地普通高校、職業院校選取機電、計算機、電子商務、英語等專業課程實施翻轉課堂教學質量評價指標部分數據樣本（見表16），第1～20組數據用于BP神經網絡的學習訓練，第21～25組數據用于BP神經網絡的測試檢驗；X11, X12, X13, …,X93為教學質量評價指標；得分（B）為翻轉課堂教學質量評價的綜合得分，由運用AHP計算得到，此得分即為BP神經網絡的期望輸出值B。

4.4 BP神經網絡評價模型實驗及結果

改進粒子群算法及BP算法參數的初始化大大影響著BP神經網絡性能，相關參數設置為：粒子群算法的最大迭代次數tmax=500，種群規模為40，慣性權重ωmax=0.8，慣性權重ωmin=0.3，變異概率g1=0.07,g2=0.45；BP算法的初始學習率（學習步長）η=0.15，動量因子β=0.75。BP神經網絡的目標誤差精度為1×10-4，BP算法最大迭代次數設定為800。借助MATLAB7.0仿真工具軟件，將表16第1～20組樣本輸入至BP神經網絡，并進行學習訓練，直至達到規定的誤差精度或最大迭代次數。BP神經網絡學習訓練誤差變化曲線如圖4所示。當訓練步數達69步時，訓練誤差便滿足目標誤差精度要求，訓練時間較短，訓練精度較高。表16第21～25組BP神經網絡測試樣本評價結果見表17。由表17可看出，測試數據用于翻轉課堂教學質量評價的BP神經網絡實際輸出值與期望輸出值的相對誤差最高不超過1.7%，BP神經網絡輸出的翻轉課堂教學質量評價等級與期望輸出完全一致。基于AHP和BP神經網絡的翻轉課堂教學質量評價模型具有很強的泛化能力，非常契合教育行業領域專家的評價思維，可比較科學、客觀、高效、精準地評價翻轉課堂教學質量。

5 結 語

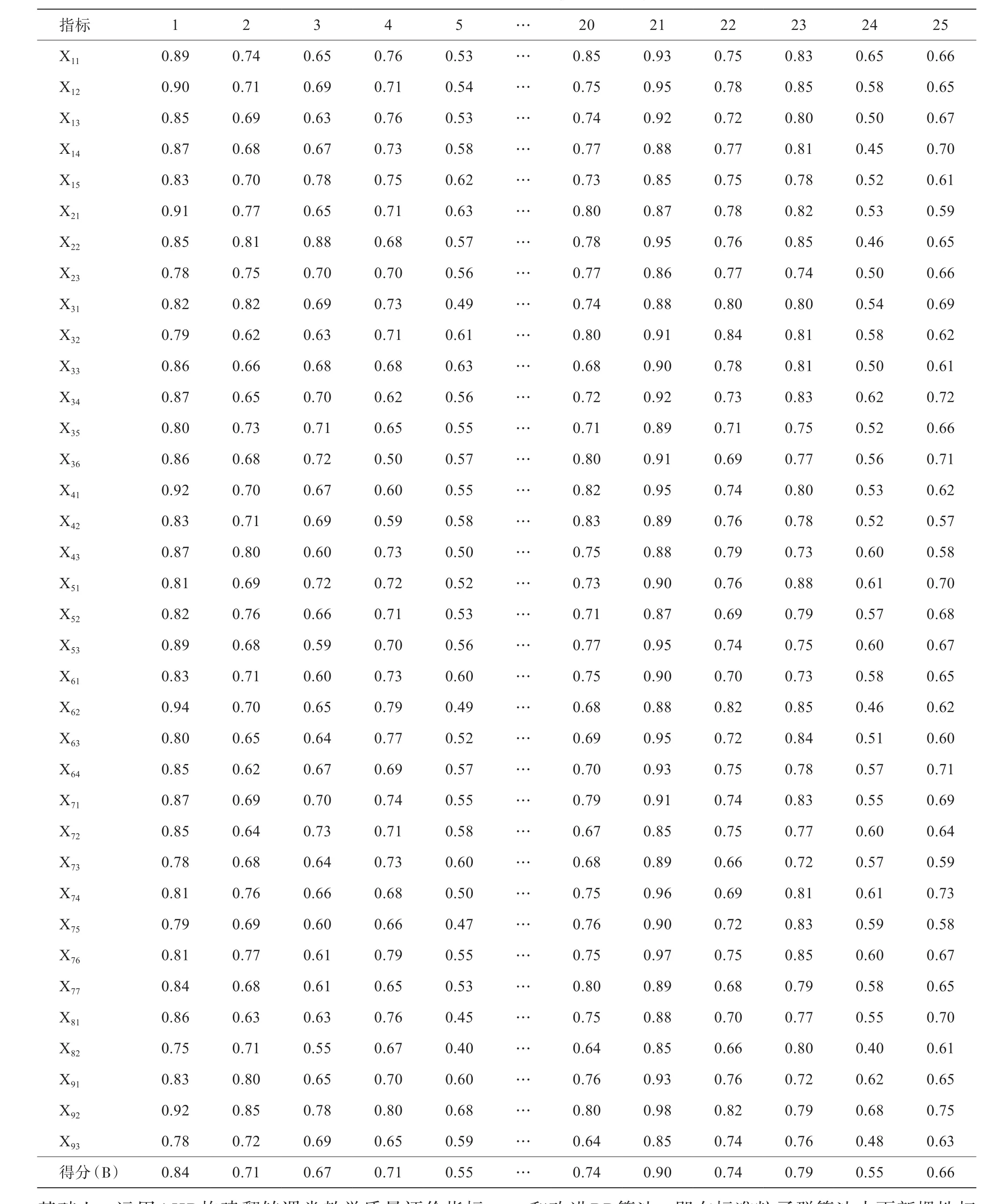
表16 BP神經網絡訓練樣本及測試樣本

本文在分析影響翻轉課堂教學質量主要因素的基礎上，運用AHP構建翻轉課堂教學質量評價指標體系，并確定各指標綜合權重，同時構建用于翻轉課堂教學質量評價的BP神經網絡模型。針對粒子群算法及標準BP算法存在的缺陷，提出改進粒子群算法和改進BP算法，即在標準粒子群算法中更新慣性權重并引入遺傳變異因子，在標準BP算法中加入動量項和自適應學習因子。采取改進粒子群算法優化輸出BP神經網絡的最佳初始權值和閾值，利用一定的樣本數據和改進BP算法對BP神經網絡加以訓練和測試。仿真實驗結果表明，該評價模型應用于翻轉課堂教學質量評價，具有評價速度快、準確度高、智能化程度高的顯著優勢，為翻轉課堂教學質量的綜合評價提供一種新的思路和方法，對職業院校的課堂教學改革、提升課堂教學質量有一定的指導作用。

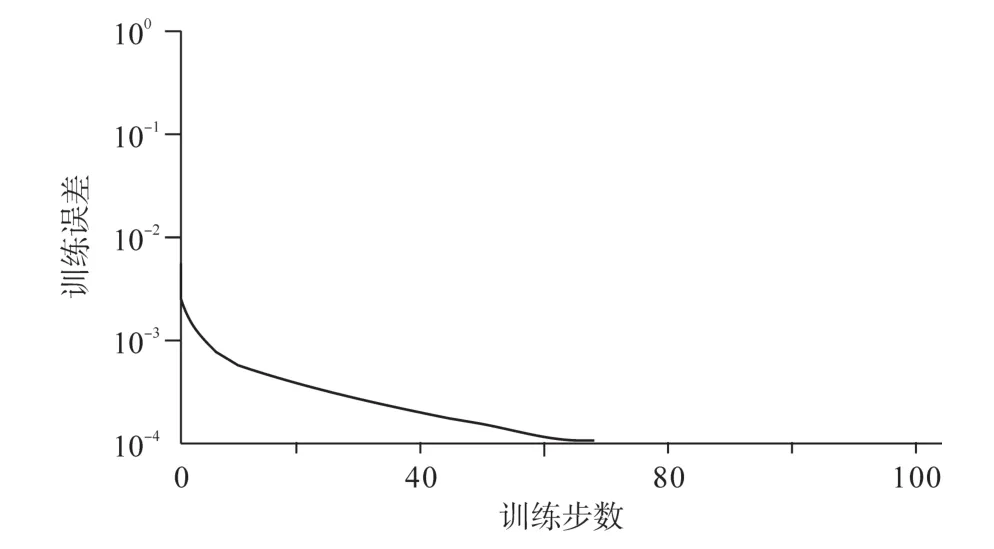
圖4 BP神經網絡學習訓練誤差變化曲線

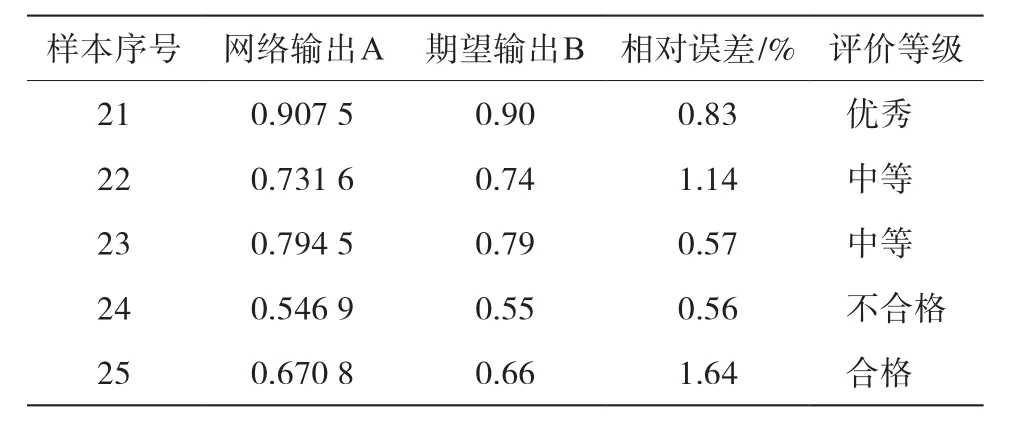
表17 BP神經網絡測試樣本評價結果