地層各組分熱中子宏觀俘獲截面Σ值的最優化確定

康曉泉,伍東,趙秀峰,何志明,盧炳文

(中國石油集團長城鉆探工程公司國際測井公司,北京100101)

0 引 言

20世紀80年代最優化開始應用于測井資料處理和解釋[1-2],目前在復雜巖性常規測井資料處理[3-4]、生產測井資料處理[5]和中子壽命測井衰減譜解譜[6]等方面廣泛應用。當測量了自然伽馬、聲波時差、密度、中子等測井曲線,因為求取的骨架體積、泥質含量和孔隙度等參數的數量少于已經測量的曲線數,可以建立最優化方程求取各項體積百分比。最優化在測井解釋中的應用傾向于與其他算法相結合的方向發展[7-9]。

通常,測井解釋最優化方法根據巖性骨架和泥質參數求取骨架體積、泥質含量和孔隙流體體積百分比。在PNN測井前,已通過其他測井獲得了骨架礦物體積含量和泥質含量,PNN測井得到的是1條地層熱中子宏觀俘獲截面Σ值的曲線。按照體積模型,Σ測井曲線應該由地層中各項物質的體積百分比與各自Σ參數相乘后再線性相加構成。但是,由于地層中硼、釓、氯等高俘獲截面元素的含量和地層水礦化度等的不同,在不同區域,骨架、泥質與孔隙流體的Σ參數有著不同的數值。因此,有必要根據實際Σ測井曲線和地層體積含量,進行地層中各項Σ參數的最優化反演。地層中各項Σ參數常用的有4～9個,而測井曲線的深度點通常遠遠大于9個,即Σ方程組是個超定方程組,可以采用最優化方法解該方程組,確定區域的各項Σ參數,進而定量計算套后含油飽和度。

1 Σ測量、解釋原理

在套管井中,可利用中子壽命測井識別儲層中的油、氣、水[10]。其原理就是測量地層的熱中子宏觀俘獲截面Σ,根據體積方程計算套后飽和度。

Σ=Σma(1-φ-Vsh)+ΣwSwφ+Σh(1-Sw)φ+ΣshVsh

(1)

式中,Σma為骨架Σ數值;Σw為水的Σ數值;Σh為烴的Σ數值;Σsh為泥質Σ數值;φ為孔隙度;Sw為含水飽和度;Vsh為泥質含量。

求取飽和度的前提是已知礦物體積百分比和地層各項Σ參數。可利用常規測井曲線求取骨架礦物和泥質體積含量。對于地層各項Σ參數,傳統的組分參數選擇方法是輸入典型骨架、泥質和流體數值,或者根據圖版、公式、統計等計算出來。

然而,巖石和孔隙流體都不是純化合物,而是多種化合物的混合物。雜質和巖石骨架的混合使Σ數值增大,因而各項Σ參數都有一定的變化范圍(見表1)。

中子壽命測井受到套管內流體、等的影響,造成Σ測井值發生整體偏差。同樣侵入帶、地層厚度的影響、放射性測井的統計漲落誤差、地層溫度和壓力、背景值都導致測井曲線Σ數值的變化,因此地層組分Σ數值往往是一組區域、經驗數值,或者稱為視地層組分參數。定量化解釋飽和度之前,首先要分析Σ測井曲線數值和優化選取區域地層中各項Σ參數。

套管和水泥環

*非法定計量單位,1 c.u.=10-3cm-1,下同

2 區域骨架參數最優化的計算方法

如果已經有了常規測井資料,在中子壽命測井前可以計算出地層巖石礦物的體積含量。假設測井第i個深度的孔隙度為φi,含水飽和度為Sw,i,泥質含量為Vsh,i,Σ測井值為Σi,則解釋計算使用的方程組為

Σi=Σma(1-φi-Vsh,i)+ΣwSw,iφi+
Σh(1-Sw,i)φi+ΣshVsh,i

(2)

如果骨架巖性單一(例如純砂巖),式(2)中地層各項Σ參數共有4個,分別是Σma、Σw、Σh和Σsh。當測井曲線深度點總數n大于4時候,式(2)為超定方程組。可以利用最優化方法得到4個Σ參數的最優解。

2.1 最優化目標函數

常用的最優化目標函數是殘差函數。但是考慮到測井曲線數值中,不同骨架的Σ參數變化較大,比如有的泥巖Σ參數約為50 c.u.,但是灰巖的Σ參數也就是10 c.u.左右,計算過程中泥質部分權重太大,需要進行歸一化處理。即測井Σi減去式(2)等號右邊函數后除以測井Σi。選取的測井深度點個數n影響到計算結果的數值大小,還需要再次對測井深度點個數進行歸一化處理,以建立標準統一的目標函數

(3)

殘差函數可以作為解釋參數質量控制的要給定量化參數。合理的地層組分Σ參數使函數殘差數值偏小,不合理的參數殘差數值增大。

2.2 選定Σ參數初始值

盡量選取100%骨架體積含量的測井段,從Σ測井曲線上讀取骨架Σ參數的初始值。即選擇純泥質地層讀取泥巖骨架Σ參數的初始值,選擇純灰巖地層讀取灰巖骨架Σ參數的初始值。

有些井不存在純骨架的地層。例如,砂巖地層有流體存在于儲層孔隙中。某些井骨架巖石和泥質有一定的混合百分比,例如泥質灰巖地層。對這些井,還需要手工計算這些巖性骨架Σ參數、油和水參數。建立未知Σ參數個數的正定方程組,根據矩陣反解各項Σ參數初始值,這一過程中選取的深度點要具有地區典型性特征。

2.3 約束條件

常規測井最優化解釋中,計算出來的體積含量之和等于1,各項Σ參數最優化方程約束條件有2個:①各項Σ參數都有一定的范圍;②歸一化的目標函數由于待優化的參數多,計算量往往較大,可以設置一個誤差范圍σ,當minf(x)<σ最優化計算結束。

2.4 井段選擇原則

優先選擇孔隙度為0的地層測井井段,這樣可以消除飽和度的影響。當骨架和孔隙并存的地層,而且有些地層飽和度不知道,要選擇流體性質已知的地層進行流體骨架參數的求取。當全井流體信息未知情況下,根據經驗,底部原先是水層的選取為水的優化參數井段,含油氣的井段要根據油田資料結合該井生產情況、實際測量曲線數值特征進行分析選取。

實際過程經常遇到選取某個井段的2個骨架參數的地層體積含量整體線性變化,即aV1Σx+aV2Σy=ΣabV1Σx+bV2Σy=ΣbcV1Σx+cV2Σy=Σc。Σx和Σy代表地層組分x,y的Σ參數;V1、V2代表地層組分的體積含量;a、b、c為系數;Σa、Σb、Σc是測井數值。例如砂巖儲層,砂巖的體積和孔隙度體積成正比變化。雖然建立的方程很多,但是整體上方程是一個欠定方程,目標函數得不到最優解。因此,建立方程時候要注意選擇不同骨架參數之間體積含量相對變化的井段,進行有效優化計算。

并非井段選擇越長越好,要根據需要計算的Σ參數合理選取井段。不同組分參數井段的選取,要進行相同比例的分配,盡量保持各個變量之間方程的等比例。

選取的井段要有典型性,能代表地區典型的巖石物理特征。

3 實際資料處理解釋應用

圖1是中亞某地區砂巖套管井PNN測井資料。第1道是常規計算出來的剖面;第3道是常規自然伽馬曲線,PNN測井時測得的自然伽馬曲線,常規自然電位曲線;第4道是根據傳統方法計算出來的含油、含水剖面,測量Σ曲線,擬合Σ曲線,殘差Σ曲線;第5道是最優化方法計算出來的含油、含水剖面,測量Σ曲線,擬合Σ曲線,殘差Σ曲線。根據孔隙度為0的地層,和頂部臨井確定為油,底部確定為水的地層,選擇了109個深度點設立最優化方程,利用MATLAB的fmincon函數進行優化計算,輸入初始化泥質、砂巖、油、水的Σ分別為傳統方法的60、30、20、65,約束各個參數數值范圍為20～80,10～50,10～30,20～100,優化后得到54.2,46.7,14.1,60.3。殘差曲線誤差經過優化后明顯變小。

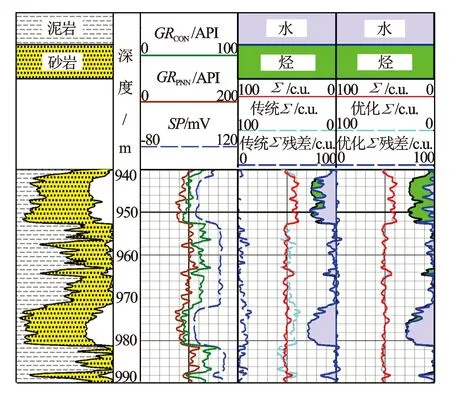
圖1 中亞某地區砂泥巖PNN測井Σ參數選取傳統和優化處理結果對比

圖2是中東碳酸鹽某儲層PNN測量曲線和處理解釋結果。常規資料是20世紀70年代測井數據。選擇巖性相對較純的泥巖、砂巖、白云巖和灰巖,以及底部水層和頂部油層資料建立方程。優化后的泥質、砂巖、灰巖、白云巖、油和水的Σ骨架分別為77.5、9.8、141、15.0、15.1、85.3 c.u.。反演的Σ在砂巖、白云巖、灰巖的油層和水層與測量的Σ油較好的相關性,但是泥巖地層部分井段誤差較大,原因是泥質Σ曲線變化較大。傳統方法在2 702～2 712 m井段解釋為油水層,但是優化后解釋為油層,射孔試油為純油層,優化后飽和更接近實際生產結果。

圖2 中東某地區復雜巖性PNN測井骨架參數選取和處理結果

4 討 論

常規測井處理解釋理論上,有些地層參數不能隨意修改。地層組分Σ參數的最優化處理不意味著任何測井曲線只要有相對變化就能接受測井質量。PNN測量的Σ的曲線首先進行原始測井資料質量控制,進行必要的環境校正,以得到真實的地區原始測量資料。

測井測前設計時,最好測量100%體積含量的不同地層參數的井段。即根據該井常規測井資料,對不同地層參數選擇100%的體積含量井段進行PNN測井,有利于確定不同地層組分的Σ數值。

對于井下飽和度未知的井段,測井前要盡量分析該地區資料,尋找儲層頂部純油、氣段和儲層底部純水段進行測量,以確定油、氣和水的Σ數值。生產歷史較長,整個井段油水情況未知,可以根據純油的Σ數值和地層水礦化度圖版上讀取的Σ數值,計算得到飽和度后,根據體積含量和地層參數反過來計算Σ曲線,和Σ測量曲線對比進行解釋參數質量控制。

5 結 論

(1)針對PNN測井解釋Σ骨架參數選擇不確定的問題,提出一種解決辦法,根據最優化計算出來的骨架參數是該井資料在設定條件下的最優解,給出解釋參數質量控制的量化指標。

(2)提出來最優化在測井解釋中的一個新的應用,與常規測井解釋最優化的思路不同,這里選擇不同井段數據對地層組分參數的最優化計算。這種思路也可以應用于自然伽馬、中子等其他測井曲線的地層組分參數確定。不同地區自然伽馬、中子地層組分數值也會由于一些原因變化較大,首先利用其他資料確定體積含量,然后采用不同井段建立最優化方程求取自然伽馬、中子的地層組分參數。