B樣條曲面拼接方法的設計與研究

吳麗娟, 韓 松, 李 博

(沈陽師范大學 物理科學與技術學院, 沈陽 110034)

0 引 言

曲面拼接在工程設計中的廣泛應用,使其成為了目前科研領域中的重要課題,而曲面拼接在許多學者的探索下,誕生了很多種曲面拼接的方法。滾動球法是由Rossignac和Requicha提出[1],滾球法可以概括為一個球與2個待拼接曲面同時相切的球滾動時形成的掃掠曲面。偏微分方程法(PDE)在幾何造型中的最初應用就是構造過渡面[2]。蒙皮是應用在飛機業和船舶業中包圍在骨架結構外形成的維形構件。蒙皮構造法由Woodward提出,這個過程就如在建造機翼時在一系列翼肋組成的骨架上加上一張蒙皮,這樣子機翼蒙皮就稱為掃掠曲面。它的主要原理是通過一個拓撲點陣,或者離散的點云,這種方法在數學上就是通過在這些點陣和截面曲線間插值來構造過渡曲面。PDE法設計曲面節省資源,條件是切觸線并計算待拼接曲面與過渡曲面的跨界導矢;構造過渡曲面只需要給出待拼接曲面邊界上的點和待拼接曲面和過渡曲面間的跨界導矢就能生成光滑過渡面;可調整待拼接曲面邊界上的點和待拼接曲面和過渡曲面間的跨界導矢來改變過渡面的形狀。偏微分方程法又相繼發展出許多新的求解過渡曲面方法,如Lihua.You[3]的先后提出的四階偏微分方程法和特征函數法。本文在查閱大量參考文獻的基礎上,設計了3個矢量參數下的求解PDE的方法,并通過該方法實現了曲面的C1連續拼接[4]。

1 B樣條曲線與曲面

1.1 B樣條曲線

B樣條曲線具有局部性、連續性、凸包性、變差縮減性等特點。

B樣條曲線定義公式:

(1)

Pi(i=0,1,…,n-1,n)為控制多邊形頂點,順序連成的折線稱為控制多邊形[5],Ni,k(t)(i=0,1,…,n-1,n)稱為B樣條基函數,它是由節點矢量的非遞減參數T的序列,由t0≤t1≤…≤tn決定的[6]。本文利用VC2010, 根據B樣條曲線基函數公式設計出B樣條曲線在控制頂點不斷變化下產生的曲線,產生曲線如圖1所示[7]。

圖1 B樣條曲線的生成Fig.1 Gernervation of B-spline curves

1.2 B樣條曲面

由于B樣條曲面的特點是局部支撐性、連續性、凸包性和變差縮減性,B樣條曲面方法可以處理曲面的重建工程, B樣條曲面造型技術廣泛的應用在工程設計中,并且成為了當今最廣泛流行的數學模型分析的主要選擇方案[8]。

圖2 B樣條曲面的生成Fig.2 Gernervation of B-spline curves

B樣條曲面是在已知參數向量u,v的節點向量u=[u0,u1,…,um+p]和v=[v0,v1,…,vn+q],p×q階B樣條曲面表達式定義如下[9]:

(2)

其中,Pi,j(i=0,1,…,m;j=0,1,…,n)是給定空間(m+1)×(n+1)個點列,構成一張離散的控制點網格,稱為B樣條曲面的特征網格。Ni,p(u)和Nj,p(v)是B樣條函數,分別由節點向量U和V按B樣條曲面基函數所得。B樣條曲面繼承了B樣條曲線的一些特性[10]。

1.3 構造B樣條曲面

首先通過讀取出2個5×5離散控制點數據來繪制出控制點網格。再在基于B樣條曲線曲面基函數公式繪制出一個基于散亂數據點B樣條曲面網格,再用相同的方法繪制出第2個基于散亂數據點下的B樣條曲面網格,這樣就繪制出了2個待拼接的曲面。

2 曲面拼接的構造

2.1 曲面拼接的偏微分方程法

在實際工程應用中,生成曲面需要以下3種條件中的一種或者幾種:1)功能上的限制,2)實際應用中的限制,3)美觀程度,這樣符合要求的曲面稱為過渡曲面。在數學上,過渡曲面的構造可以看作求解:在已知待拼接曲面邊界上的點的曲面上,計算出待拼接曲面間符合待拼接曲面邊界上點的函數曲面w(u,v),典型的待拼接曲面邊界上的點是以w及其偏導數在給定待拼接曲面邊界上點的值的形式給出的,偏導數的階數由過渡曲面與待拼接曲面間的連續性要求所決定[11]。

本文采用偏微分方程法生成過渡面的實現:1)首先設計偏微分方程過渡曲面表達式,2)求得待拼接曲面邊界上的點,3)計算偏微分方程,4)求得待拼接曲面。關鍵步驟就是如何求解偏微分方程。本文主要闡述了在3個矢量參數下的求解PDE的方法,并通過該方法實現了曲面的C1連續拼接[12]。

2.2 拼接算法實現

設待求過渡曲面的表達式為:

(3)

為了實現曲面的拼接,設計運用3個矢量參數的4階偏導數實現曲面的C1連續。

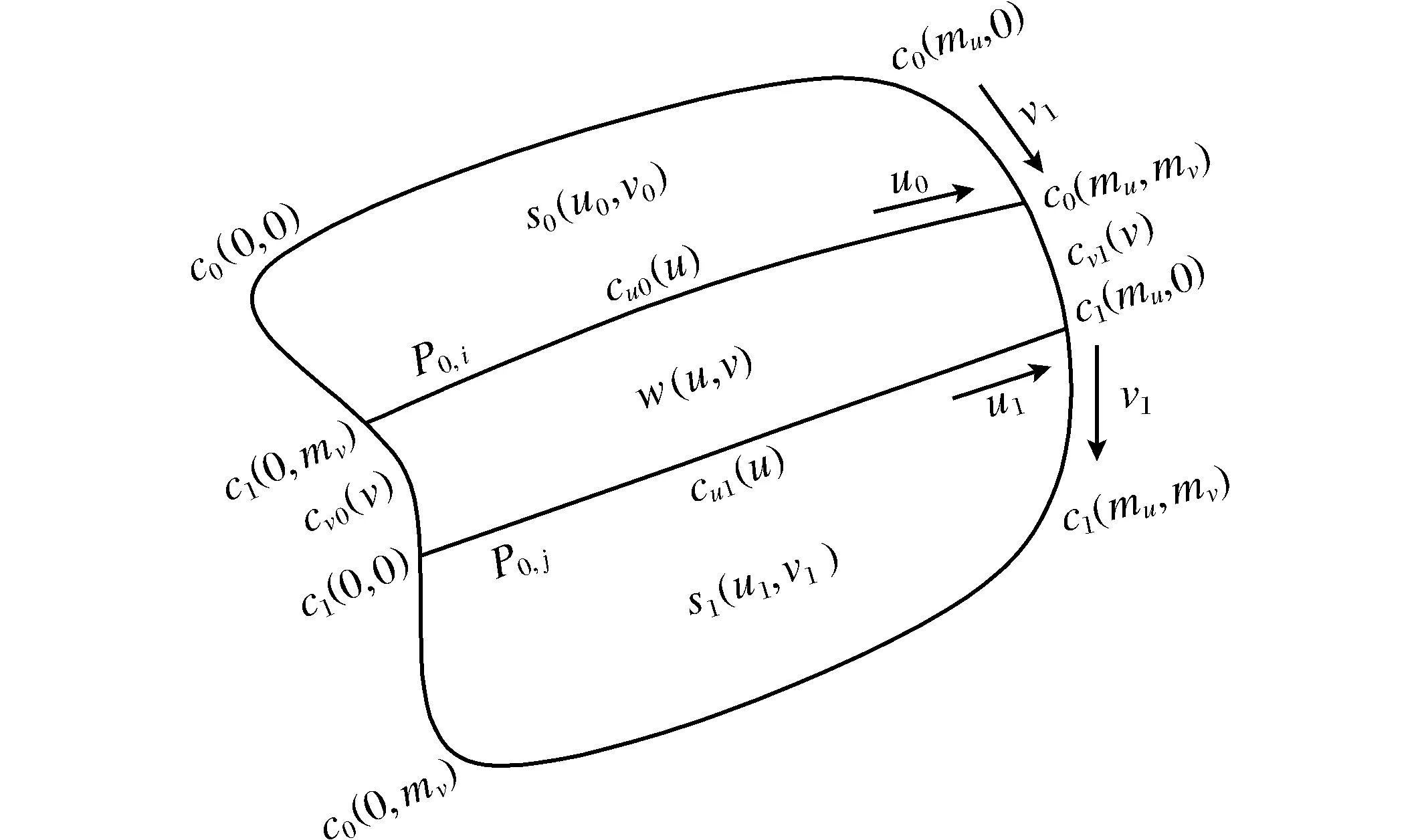
圖3 過渡曲面與原曲面位置關系及符號Fig.3 Symbol of relation between transition and original surface

為了實現曲面的C1連續,首先構造偏微分方程表達式:

(4)

這里w=w(u,v)表示待生成的過渡曲面,a=[axayaz]T,b=[bxbybz]T,c=[cxcycz]T是3個矢量值參數也就是形狀參數。因此如果w(u,v)邊界線與2個待拼接曲面的過渡切觸線能夠達到一階(C1)連續,那么生成的過渡曲面也是滿足C1連續的[13]。

根據曲面C1連續的條件,為了求得w(u,v)的表達式,首先需要知道2個待拼接曲面的邊界條件,構造待拼接兩曲面邊界滿足如下定義:

(5)

其中,G1(v)、G3(v)是2個曲面的邊界曲線,G2(v)、G4(v)是邊界曲線的一階導,G1(v)、G2(v)是其中一個待拼接曲面邊界上的點,G3(v)、G4(v)是另一個待拼接曲面邊界上的點,如果w(u,v)符合等式(5)的要求,則w(u,v)一定就與2個待拼接曲面達到C1連續。因為直接求解w(u,v)的表達式是非常困難的,而且在邊界上w(u,v)都是關于v的函數,下面采取如下方法求解w(u,v)的近似表達式[14-15]。Gi(v)i=1,2,3,4通常都是簡單函數的集合,所以設計下面的方程來重新表達Gi(v):

(6)

(7)

為了求解式(6),先引入半解析法,轉換成如下形式:

(8)

將式(8)代入到式(7)當中去,則有:

(9)

將式(9)代入到式(8)當中去,則有可得到ci0,ci1,ci2,bi1,bi2的值,則有:

可得:

(11)

為了驗證本算法,分別設3個形狀參數:ax=ay=az=1,bx=by=bz=4,cx=cy=cz=9求得x,y,z的表達式分別如下:

(12)

那么接下來就是求解未知常數ax10,ax11,ax12,ax13,ay10,ay11,ay12,ay13,az10,az11,az12,az13,首先根據邊界條件(5)、(6)求得az10,az11,az12,az13的值az10=3,az11=-4,az12=8,az13=6,最后求得x,y,z的表達式為:

(13)

雙圓柱曲面拼接結果如圖4所示。

圖4 通過改變控制矢量實現的曲面拼接的改變Fig.4 Realize the change of surface joining by change control vector

分別是ax=ay=az=1,ax=ay=az=2,ax=ay=az=3,可以發現當a的數值發生變化時,拼接曲面的改變會比較大。

3 結 論

在綜合論述B樣條曲線曲面生成原理的基礎上設計了通過3個矢量形狀參數4階偏微分方程的算法來完成B樣條曲面C1連續拼接,較好的解決了曲面形狀微調的問題,有利于曲面形狀的控制,而且在曲面閉合的情況或非閉合情況下都可應用,能夠較好的滿足實際需要,為曲面的光滑拼接的研究提供了理論基礎。本算法實現了一階連續曲面拼接,在此基礎上可擴展到對高階連續曲面的拼接需求,滿足實際工程領域的需要。