基于逐步回歸的穩健估計和異常值檢測

崔 樂, 吳 迪, 成麗波

(長春理工大學 理學院, 長春 130022)

0 引 言

近年來,異常值檢測一直是統計診斷中一個比較活躍的研究課題。在實際生活中,由于種種原因不能夠和其他數據一起用于多元統計的線性回歸模型中的值,稱為異常值。換句話說,參數估計、模型構建及預測都會受到異常值的影響,因此,這篇文章主要研究的是基于逐步回歸的穩健估計和異常值的檢測。

比較常見的統計量有殘差、學生化殘差、Cook距離以及W-K統計量等。殘差和學生化殘差[1-3]都可以用來檢測異常值,但是殘差沒有考慮到異方差性,而學生化殘差考慮到了這一點,因此用學生化殘差檢測異常值比用普通殘差更有效。而Cook距離和W-K統計量[4-6]僅可以判斷出數據是否有強影響點,但是異常點和強影響點之間沒有必然的關系,即異常點不一定是強影響點,強影響點也不一定是異常點。

本文基于逐步回歸模型,從殘差平方和的角度出發,研究出檢測異常值的方法,并估計異常值的大小。通過與傳統方法的比較,驗證該方法的有效性。

1 逐步回歸

在多元線性回歸模型中,自變量的選擇實質上就是模型的選擇。現設一切可供選擇的變量是t個,它們組成的回歸模型稱為全模型(記m=t+1),在獲得n組觀測數據后,有模型

其中:Y是n×1的觀測值,β是m×1未知參數向量,X是n×m結構矩陣,并假定X的秩為m。

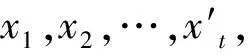
β=(βp,βq)′,X=(Xp?Xq)

下面從不同的角度給出自變量選擇的準則[7]。

準則1 平均殘差平方和達到最小

準則2CP統計量達到最小

該準則是由馬斯洛于1964年從預測的角度提出:

準則3 AIC準則

該準則由日本統計學家赤池弘次于1974年根據極大似然估計原理提出:

AIC=nln(SSEP)+2P

其中:SSEm是m個自變量x1,x2,…,xm所對應的殘差平方和;SSEP是p個自變量x1,x2,…,xp所對應的殘差平方和。

快速選擇變量的算法有很多,例如:向前法、向后法、逐步回歸法[7]等,其中逐步回歸法是應用最廣的一種方法。它的具體做法是先將變量一個一個的引入,當引入到第3個變量之后的每一步,首先對已引入的變量進行剔除。這樣,自變量將不斷的引入、剔除、再引入、再剔除……直到自變量不能被剔除,同時也無法引入自變量為止。

2 基于逐步回歸的殘差平方和

經過逐步回歸后生成最優多元線性回歸模型如下:

yi=β0+β1xi1+β2xi2+…+βpxip+εi,i=1,2,…,n

(1)

其中:p為解釋變量的數目;βj(j=0,1,…,p)為回歸系數;εi為隨機誤差,且εi～N(0,σ2),i=1,2,…,n;β=(β0,β1,…βp)T;σ為未知參數。

均值漂移模型[8-9]是在第i個數據點上增加一個漂移項δ,即在這個數據點yi處的均值發生了非隨機漂移,若δ顯著不等于零,則yi處的均值發生了漂移,說明此點為異常點。

由于事先不知道在線性模型中出現異常值,因此,可以先假定模型中沒有異常值,其線性模型的矩陣形式為

Y=Xβ+ε

(2)

其中

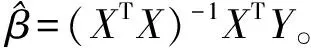
SSE=YT(I-H(X))Y

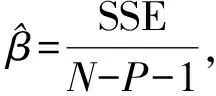
殘差平方和(SSE)會受到異常值大小的影響,即隨著異常值的增加,殘差平方和(SSE)也增加。

3 異常值的檢測

基于均值漂移模型,假設模型中的第i個觀測值為異常值,即異常值的大小為δi,其余的皆為正常數據,計算此時的殘差平方和(SSEi)為

(3)

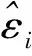
(4)

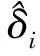
(5)

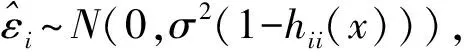
4 穩健估計和異常值的識別

4.1 標準差的穩健估計

M估計是基于最小二乘估計發展起來的一種抗差估計(Robust Estimation)方法[10-12],是由huber于1964年最先提出來的,也稱為廣義最大似然估計。M估計已經成為最經典的一種穩健估計方法。

M估計的估計方程寫成矩陣形式是這樣的:

XTWXβ=XTWY

(6)

迭代公式如下:

(7)

其中:W是以ωi,i=1,2,…,n為對角線的權矩陣;X是解釋變量矩陣,X=(x1,x2,…,xn);Y是因變量向量,Y=(y1,y2,…yn)T。

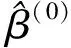
4.2 異常值的識別

5 模擬與實例分析

5.1 模擬實驗

假設有一多元線性回歸模型y=3+5x1-4x2+4x3-3x4+x5-2x6+2x7-x8+3x9+6x10+ε,現利用計算機模擬產生100個數據樣本。下面考慮3種方案進行實驗。

方案1 將大小為5.5的異常值加入到第49個樣本觀測值中。

方案2 將大小為6,-5的異常值分別加入到第31和69個樣本觀測值中。

方案3 將大小為-6.5, 5.5, 4.5, -3的異常值分別加入到第48～52個樣本觀測值中。

1) 異常值檢測

對于3種方案的D統計量如圖1所示。圖1是基于M估計的D統計量,由圖1(a)可以看出,第50個觀測值對應的D統計量遠大于3,判定為異常值。同樣由圖1(b)可以看出,第32個和第70個觀測值為異常值;由圖1(c)或者看出,從第49～53個觀測值均被檢測出異常值。由此可以看出該檢測異常值的統計量可以很好地檢測出異常值,并且由于方案3是5個連續的異常值,因此說明此方法對異常值的遮蔽現象有一定的作用,能夠有效地檢測出連續幾個異常值。

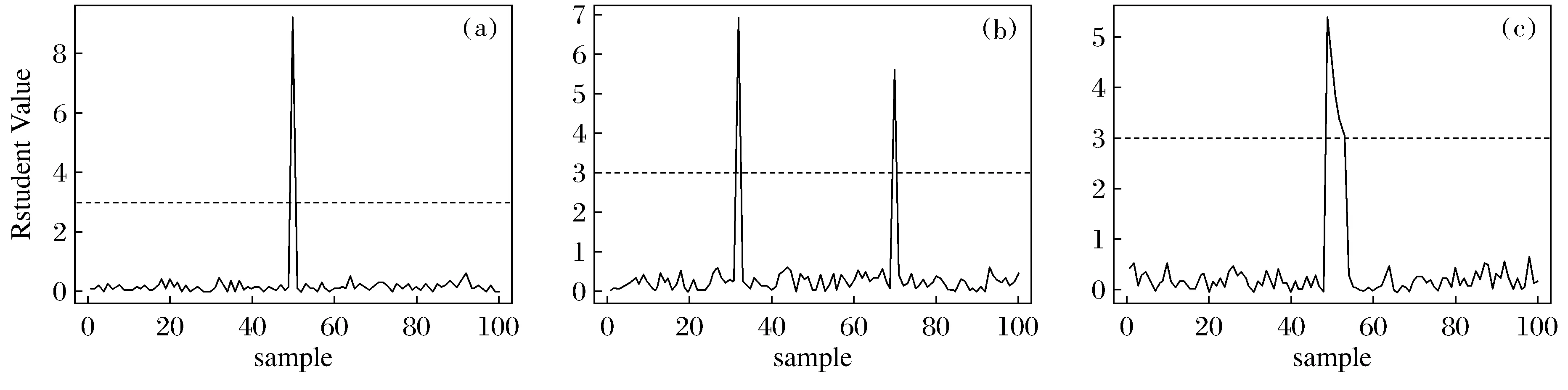
圖1 方案1～3的基于M估計的D統計量Fig.1 D Statistics Based on M Estimation for Schemes 1～3

圖2是方案1～3中每個樣本觀測值的學生化殘差示意圖。按照傳統的方法,將觀測值的學生化殘差的絕對值大于3的認為是異常值。從圖2(a)中可以看出,無法準確地檢測出方案1中異常值,圖2(b)中,可以很好地檢測出方案2中的異常值,從圖2(c)中,學生化殘差只能檢測出第49, 50, 52, 53個觀測值為異常值。由此可以說明,用新構建的基于穩健估計的D統計量比傳統的學生化殘差檢測異常值更加有效。

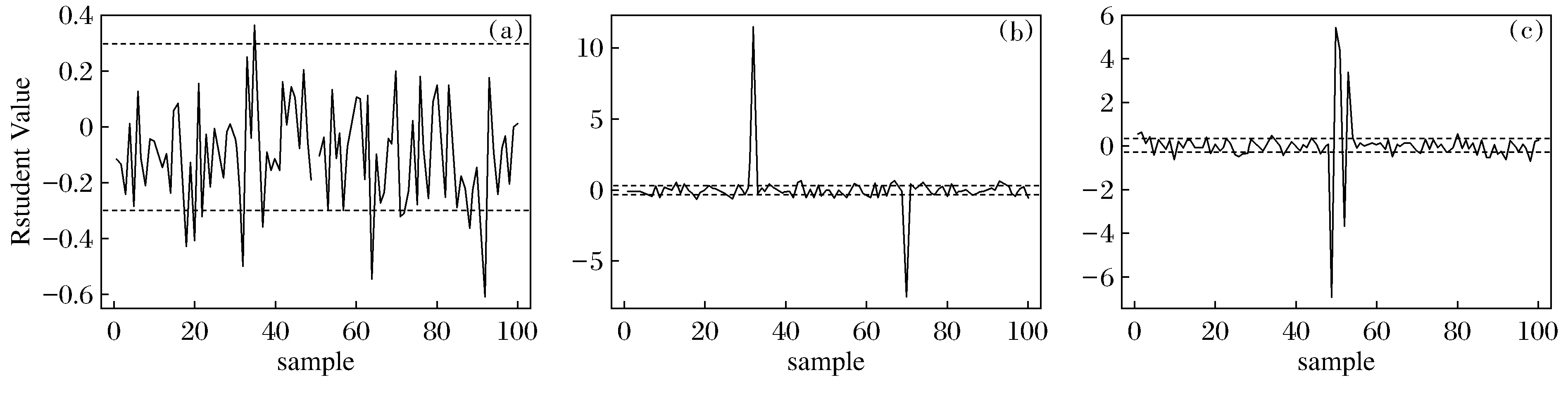
圖2 方案1～3的學生化殘差Fig.2 Student Residual in Scheme 1～3

2) 異常值大小的估計

通過公式(4)來計算異常值的大小,表1是3種不同方案的異常值大小的評估值。從表中可以看出,對于方案1～2,本文構建的統計量都可以很好地檢測出異常值的大小。對于方案3異常值大小估計精確度不如方案1～2,但仍然還是比較準確的。

表1 基于方案1～3的異常值大小估計值Tab.1 Outlier size estimates based on Schemes 1～3

5.2 實例分析

在房地產行業中,影響房屋價值的因素有很多。本實例中,根據房屋價值的影響因素及人們的偏好,記錄的影響房屋價值的指標包括面積、戶型、當前樓層、總樓層、朝向、裝修情況。其中,戶型為幾室幾廳,可以分開作為單獨變量;當前樓層分為底層、中層和高層;朝向分為北、東北、東、東南、南、西南、南北、西、西北、東西;裝修情況分為毛坯、普通裝修、精裝修。

房價和房屋面積需要以10為底取對數,目的是降低房價和面積的數量級,提高模型估計精度。戶型是一個連續的數值變量,可以不用修改。其他的字符型變量則需要進行量化。樓層包括3種,根據計量經濟學知識,本方案將采用2個0-1變量(構成一個二維行向量)度量該3種類型。例如,(0,0)代表低層,(1,0)代表中層,(0,1)代表高層。其他分類指標同樣需要進行類似處理。本文選取河北省邯鄲市某小區的樣本數據。

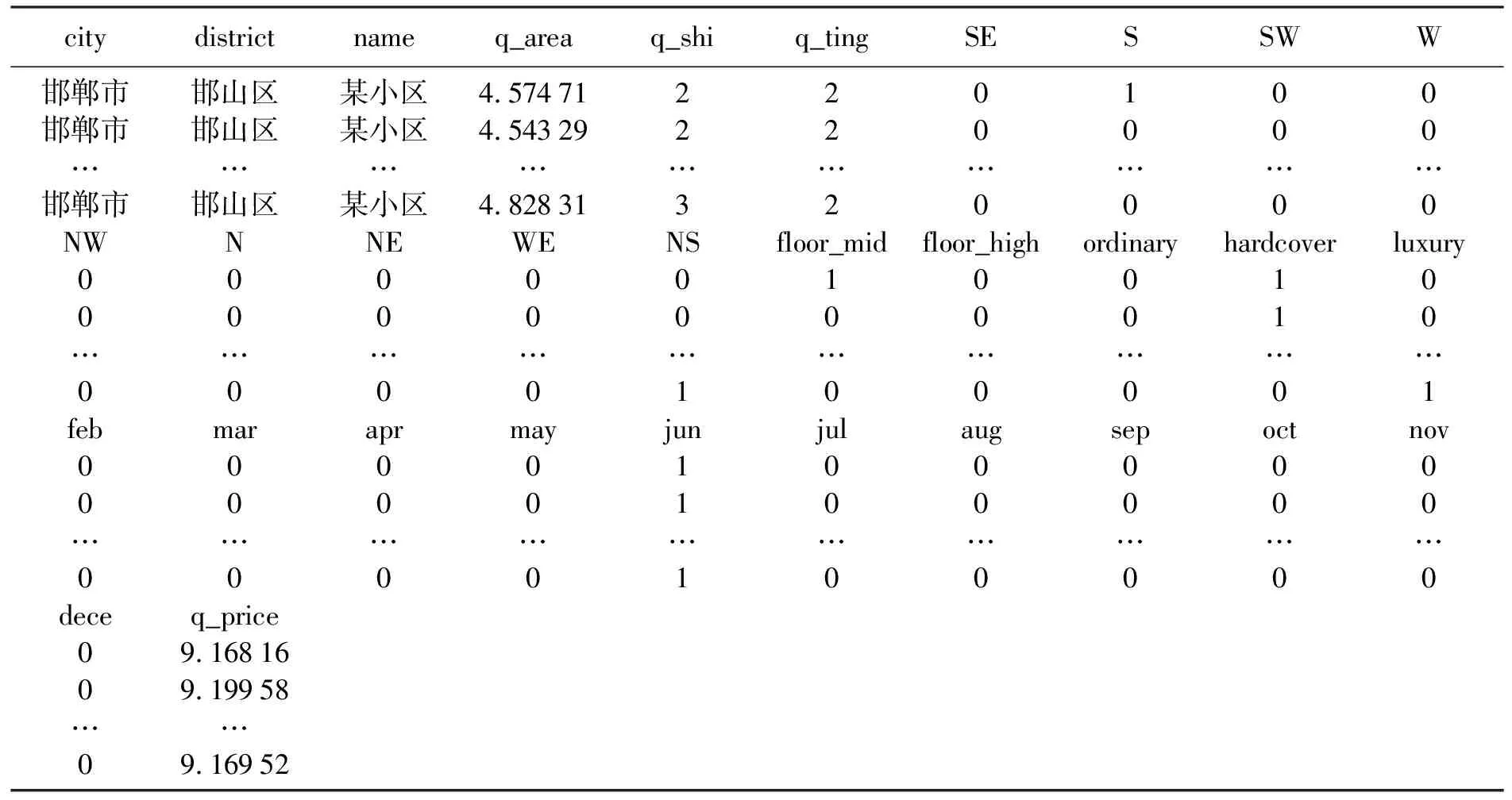
表2 河北省邯鄲市某小區的樣本數據Tab.2 Sample data of a residential district in Handan city, Hebei province

該實例的線性回歸模型為

經過逐步回歸之后所得到的“最優”回歸模型為

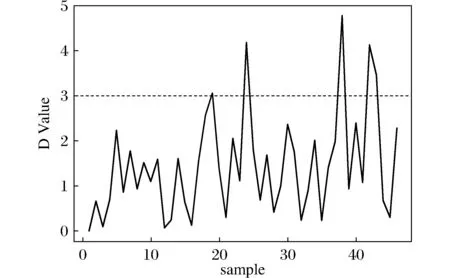
圖3 基于M估計的D統計量Fig.3 D StatisticsbBased on M estimation

1) 異常值檢測

從圖3可以看出,第24,38,42,43個樣本的對應的D統計量大于3,可判斷為異常值,其中雖然第42和43的樣本連續異常,但仍然能夠被很好地檢測出來,再一次證明此方法對異常值的遮蔽現象有一定的作用,能夠有效地將連續幾個異常值檢測出來。

2) 異常值大小的估計

同樣,由公式(4)估計出異常值的大小,估計結果如表3所示。

表3 異常值大小的估計值Tab.3 Estimates of the size of outliers

6 結 語

異常值檢測是當前數據分析研究中的一個熱點問題。通過大量的模擬實驗和實例分析,得到這樣的結論:基于M估計的D統計量可以很好地檢測出異常值,尤其是對異常值的遮蔽現象有一定的作用----能夠有效地檢測出連續的幾個異常值。