短型熱電偶導熱誤差影響因素數值仿真分析
莫建偉,荊卓寅, 李 彤,王 勇,李龍飛
(1.西安航天動力研究所,陜西 西安 710100;2.中國長城計量測試技術研究所,北京 100095)
0 引言
在先進航空航天發動機技術的研究中,經常會遇到高溫、高速氣流溫度測試問題[1]。例如:在液體火箭發動機熱試車中,溫度參數的準確測量對于衡量發動機的性能是至關重要的。由于熱電偶測溫方法具有造價低廉、使用方便等特點,目前在工程上廣泛采用,然而測溫熱電偶通常工作在高溫、高壓、高速流動環境下,熱電偶與燃氣、周圍冷壁存在輻射換熱,并且沿偶絲向熱電偶殼體存在熱傳導損失,電偶的指示值是熱電偶接點與周圍環境換熱形成的熱平衡溫度,并非測點處燃氣的真實溫度[2-5]。通常高溫測量誤差包含輻射誤差、導熱誤差以及速度誤差等,輻射誤差相對于導熱誤差而言所占份額較大,在研究過程中一般采用忽略導熱誤差的方法以簡化計算[6-10]。然而在火箭發動機的溫度測量過程中,由于測溫傳感器強度等因素的限制,傳感器深入流道內的尺寸很短,這樣會產生很大的導熱誤差,而準確評估導熱誤差的大小對發動機的性能測量以及發動機工作狀態的判定具有非常重要的意義。
針對這一情況,本文專門開展了溫度傳感器導熱誤差的數值仿真分析,研究在發動機實際氣流速度條件下,溫度傳感器長徑比以及支座溫度對導熱誤差的影響,獲得發動機實際工況條件下短型熱電偶溫度傳感器導熱修正系數,提高測量準確度。
1 數值仿真方法及準確性分析
1.1 數值仿真方法
短型熱電偶采用鎧裝結構,熱電偶在流道安裝簡化模型如圖1所示,為了消除輻射誤差的影響,流道壁溫設定與氣流溫度一致,流道壁厚2 mm。采用Ansys軟件進行數值模擬,選用RNGκ-ε湍流模型,標準壁面函數法,二階迎風格式、耦合隱式求解,氣流通道內的速度和溫度壁面條件分別取壁面無滑移、等溫邊界條件。氣流通道分別取壓力進口和壓力出口,冷卻壁處溫度設置為測溫傳感器的冷端溫度。流體區域和熱電偶殼體固體區域采用熱固耦合。
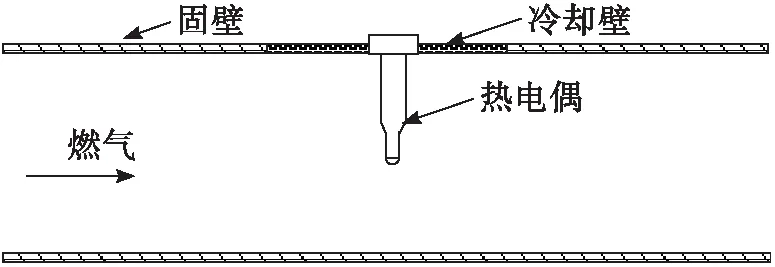
圖1 短型熱電偶安裝簡化模型Fig.1 Sketch of short type thermocouple installation model
1.2 數值仿真方法準確性分析
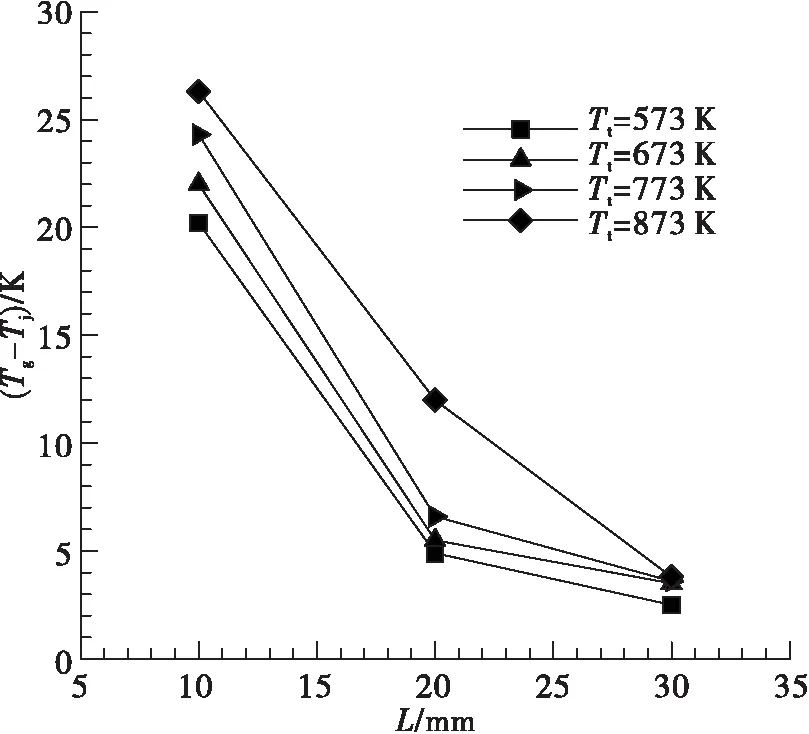
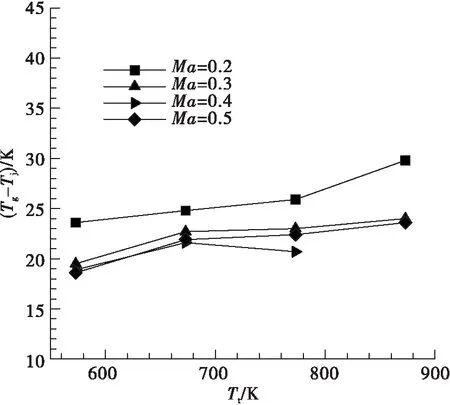
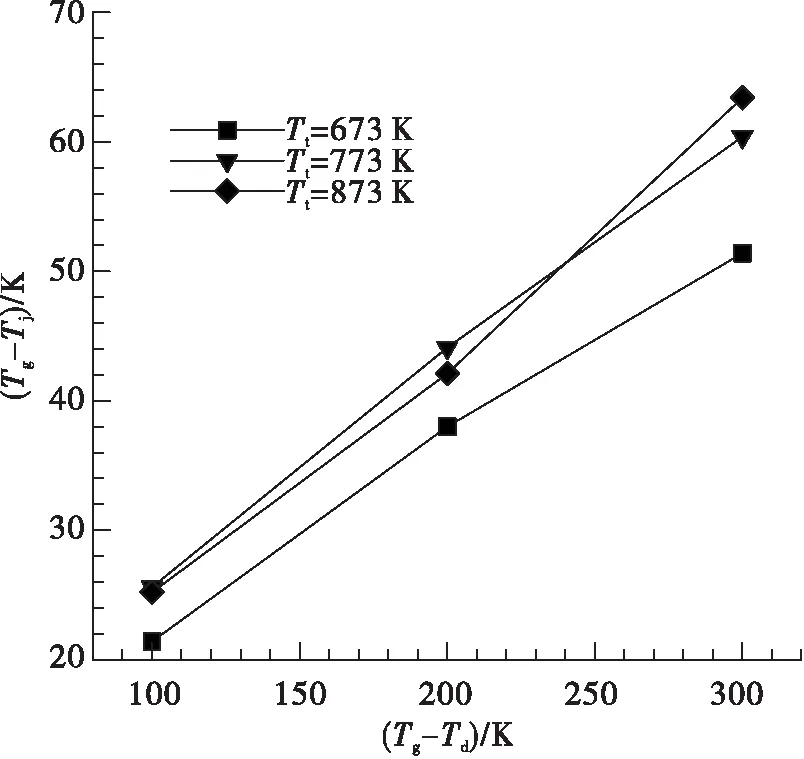
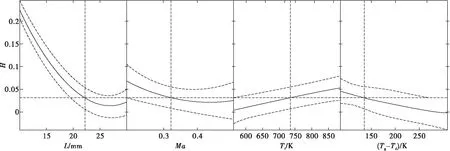
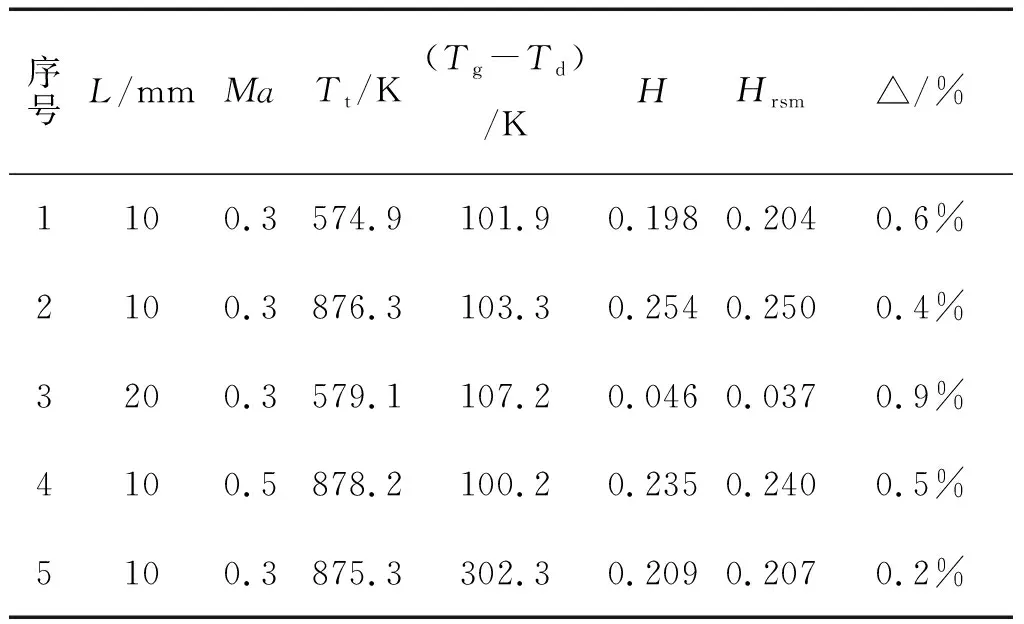
為了驗證數值仿真的準確性和可靠性,根據NACA研究報告中提供的氣流繞流熱電偶絲的導熱誤差相關試驗數據[2,11],在相同工況下采用Ansys軟件進行仿真計算,并與文獻[2]中的導熱誤差修正系數對比來驗證仿真結果的準確性。圖2為文獻[2]中的氣流繞流熱電偶絲示意圖,熱電偶絲總長為L,L/2處為熱電偶接點,基座處溫度為Tb,基座處溫度小于氣流溫度Tb 由表1中參數可得氣流雷諾數Re=3 690,由文獻[2]中努賽爾數的計算方式: 式中:Re為雷諾數;Pr為普朗特數。 可得:Nu=24.8 從而有:h=Nuλ/d=917 W/(m2·K) 文獻[2]中給出熱電偶絲在此工況下的導熱誤差修正系數約為H=0.16。 圖2 氣流繞流熱電偶絲Fig.2 Airflow passes around thermocouple wire ρ/(kg·m-3)V/(m·s-1)Tt/Kd/mL/mPr0.417164.78500.0020.020.59 為了校驗數值仿真的準確性,建立了氣流繞熱電偶絲的幾何模型,并采用Ansys軟件進行相同工況下的導熱誤差仿真計算[12]。 根據數值計算可得熱電偶表面平均換熱系數為: 式中:Q為熱電偶絲向外部導熱量;A為電偶絲表面積;ΔT為流體與熱電偶絲的平均溫差。這與從文獻[2]中得到的換熱系數917 W/(m2·K)非常接近。 另外提取仿真結果中熱電偶絲接點處的溫度可得導熱誤差修正系數: 這與文獻[2]中查到此工況下的導熱修正系數0.16非常一致。 上述計算結果表明,無論是熱電偶絲表面平均換熱系數還是熱電偶絲導熱誤差修正系數,仿真結果與文獻[2]中的結果都非常一致,這也驗證了數值仿真的準確性。 熱電偶導熱誤差理論估算公式如[13]: 式中:Tg為氣流總溫;Tj為熱電偶溫度示值;Td為支座溫度;α為熱電偶端與流體的對流換熱系數;L為傳感器插入深度;d為傳感器直徑。 對于特定的熱電偶,λ和d已經確定,在測量中影響導熱誤差的主要因素有熱電偶插入深度、對流換熱系數和支座溫度,而對流換熱系數主要受來流總溫和速度影響。下面將通過數值仿真分別研究熱電偶插入深度、來流總溫、來流馬赫數以及基座溫度對熱電偶導熱誤差的影響。 來流馬赫數為0.3,來流總溫分別為573 K,673 K,773 K,873 K,在此條件下分別研究熱電偶插入深度30 mm,20 mm和10 mm情況下導熱誤差的變化。 圖3給出了不同來流總溫條件下熱電偶導熱誤差隨插入深度的變化,可以看出,當熱電偶插入深度為30 mm時,熱電偶導熱誤差約為4 K。隨著熱電偶插入深度的減小到20 mm,導熱誤差增加到7K左右,但當熱電偶插入深度減小到10 mm時,導熱誤差迅速增大到20~30 K,這主要是由于熱電偶插入深度較短時,熱電偶導熱熱阻減小使得導熱誤差增大[14]。 圖4為不同來流馬赫數情況下導熱誤差隨總溫的變化趨勢,可以看到,不同的來流馬赫數情況下導熱誤差都表現出隨總溫升高而增大的趨勢,這是由于總溫升高后,熱電偶殼體導熱率增加使得導熱熱阻降低,導熱誤差增大。在同一總溫下,導熱誤差表現出隨馬赫數增大而減小的趨勢,這是由于隨著馬赫數的增大,氣流的特征雷諾數增大,從而使氣體與熱電偶的對流換熱系數增大,由導熱誤差理論估算公式[13]可知,熱電偶導熱誤差減小。 圖3 不同總溫下導熱誤差隨插入深度的變化Fig.3 Variation of thermal conductivity error with insertion depth at different total temperatures 圖4 不同馬赫下導熱誤差隨總溫變化關系Fig.4 Variation of thermal conductivity error with total temperature at different Mach 圖5為不同總溫下熱電偶導熱誤差隨Tg-Td的變化關系,其中Tg-Td為氣流總溫與基底溫度的差值,Tg-Td越大表示基底溫度越低。從圖5中可以看出,在不同的來流總溫情況下,熱電偶導熱誤差隨Tg-Td增大而增大,相同的Tg-Td情況下,氣流總溫越低熱電偶導熱誤差越小。 圖5 不同總溫下熱電偶導熱誤差隨基底溫度的變化Fig.5 Variation of thermocouple conduction error with substrate temperature at different total temperature 從以上熱電偶導熱誤差的仿真結果中可以看到,不同熱電偶插入深度、氣流馬赫數、氣流總溫以及基底溫度都會對熱電偶導熱誤差產生影響。為了綜合分析各因素對導熱誤差修正系數的影響程度,根據上述計算中不同工況下導熱誤差的結果,建立導熱誤差修正系數與熱電偶插入深度、氣流總溫、氣流馬赫數和基底溫度的響應面模型。 假設導熱誤差修正系數模型為二階響應面模型,并且不考慮交叉項的影響。影響導熱誤差修正系數的因素分別為熱電偶插入深度L,氣流馬赫數Ma,氣流總溫Tt以及總溫與基底的溫差Tg-Td,則導熱誤差修正系數響應面模型的數學表達式為: H=β0+β1L+β2Ma+β3Tt+β4(Tg-Td)+ β5L2+β6Ma2+β7Tt2+β8(Tg-Td)2 上式中共有9個未知數,分別為β0…β8,根據上述計算結果擬合可得: β=[0.571 3,-0.036 97,-0.684 5,0.000 197 3,-0.000 382 7,0.000 680 8,0.783 8,-2.913 3×10-8,4.173 7×10-7] 圖6為擬合得到的導熱誤差修正系數與各因素之間的關系,其中實線表示擬合曲線,而虛線為置信區間,可以看到,熱電偶插入深度對導熱誤差影響最大,插入深度較小時,導熱誤差很大,隨著熱電偶插入深度增加,導熱誤差迅速減小并趨于一個很小的值,此情況下可認為導熱誤差為零,因此在實際測量中應選擇合適的熱電偶插入深度,減小測量誤差。導熱誤差修正系數隨氣流馬赫數增大而減小,但其變化幅度較小并隨馬赫數增大而逐漸趨于平緩。導熱誤差修正系數隨氣流總溫增加呈現近似線性增加,而導熱誤差隨Tg-Td的增大呈現近似線性的減小,氣流溫度變化對誤差的影響主要原因是溫度變化造成了熱電偶殼體平均熱導率的變化,從而使導熱熱阻發生變化。 為了評估獲得的導熱誤差修正系數響應面模型的準確性,表2是不同工況下響應面模型的計算值和真實值的比較,其中Hrsm是響應面模型的計算值,H為相同工況下的真實值,可以看到,二者之間差別非常小,這說明建立的導熱誤差響應面模型是準確可信的。 圖6 導熱誤差修正系數與各影響因素之間的關系Fig.6 Relationship between thermal conductivity error correction coefficient and various influencing factors 序號L/mmMaTt/K(Tg-Td)/KHHrsm△/%1100.3574.9101.90.1980.2040.6%2100.3876.3103.30.2540.2500.4%3200.3579.1107.20.0460.0370.9%4100.5878.2100.20.2350.2400.5%5100.3875.3302.30.2090.2070.2% 建立了短型熱電偶溫度傳感器導熱誤差仿真模型,通過與國內數據對比驗證了仿真模型的準確性。接著通過仿真計算,研究了不同熱電偶插入深度、不同來流馬赫數、不同來流總溫和不同基底溫度對導熱誤差修正系數的影響規律,并建立了導熱誤差修正系數的響應面模型。主要有以下結論: 1)在熱電偶導熱誤差影響因素中,插入深度影響最大。熱電偶導熱誤差隨插入深度減小迅速增大,當熱電偶插入深度為30 mm時,熱電偶導熱誤差約為4 K。但當熱電偶插入深度減小到10 mm時,導熱誤差迅速增大到20~30 K。 2)相同的來流馬赫數情況下,導熱誤差隨總溫升高而增大,這是由于總溫升高后,熱電偶殼體導熱率增加使得導熱熱阻降低,導熱誤差增大。在同一總溫下,導熱誤差表現出隨馬赫數增大而減小的趨勢,這是由于隨著馬赫數的增大,氣流的特征雷諾數增大,從而使氣體與熱電偶的對流換熱系數增大,熱電偶導熱誤差減小。 3)導熱誤差修正系數隨Tg-Td的增大而減小,這種變化趨勢主要原因是當Tg-Td增大時,Td變小使得熱電偶殼體的平均熱導率降低,導熱熱阻增加,從而使導熱誤差修正系數減小。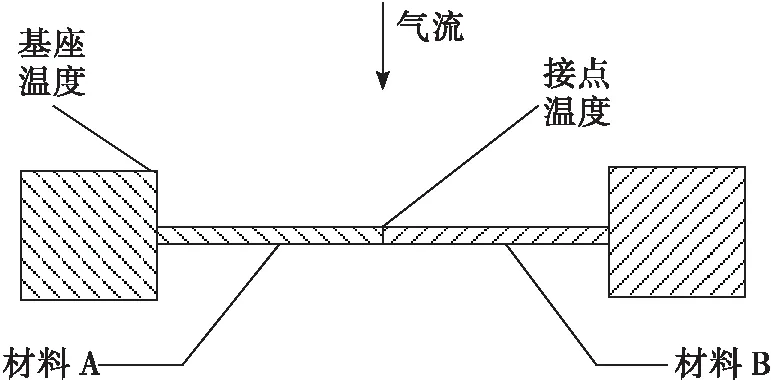

2 數值模擬結果分析
2.1 熱電偶插入深度對導熱誤差的影響
2.2 不同工況對熱電偶導熱誤差的影響研究
2.3 不同基底溫度對熱電偶導熱誤差的影響研究
2.4 導熱誤差修正系數數學模型
3 結論

