重復使用液體火箭發(fā)動機結構可靠性分配
楊進慧,戚亞群,金 平,蔡國飆
(1.北京航天動力研究所,北京 100076; 2.北京航空航天大學,北京 100191)
0 引言
重復使用液體火箭發(fā)動機的使用壽命長,同時需要在重復使用全過程中保證發(fā)動機的結構可靠性。相比于一次使用火箭發(fā)動機,對發(fā)動機的結構可靠性提出了更高的要求。
現(xiàn)有的液體火箭發(fā)動機結構可靠性分配主要是對使用壽命末時刻的結構可靠度進行分配。對于不考慮維修的重復使用液體火箭發(fā)動機,若只簡單地對使用壽命末時刻的結構可靠度進行分配,雖然可以使發(fā)動機系統(tǒng)在使用壽命末時刻滿足結構可靠性要求,但由于各子系統(tǒng)的結構可靠度函數(shù)存在差別,易導致在重復使用過程中的某一時期,各子系統(tǒng)的結構可靠性存在較大的差異,使得某些子系統(tǒng)成為系統(tǒng)中的“短板”,而有些子系統(tǒng)存在一定程度的可靠性余裕。因此,在進行重復使用火箭發(fā)動機的結構可靠性指標分配時,考慮重復使用全過程中的可靠性偏差對發(fā)動機系統(tǒng)的可靠性指標分配具有重要意義。
在液體火箭發(fā)動機中任一子系統(tǒng)的故障都可能直接導致發(fā)動機系統(tǒng)故障,故在發(fā)動機的結構可靠性設計工作中,一般將火箭發(fā)動機系統(tǒng)看作串聯(lián)系統(tǒng),對于無約束的系統(tǒng),一般可采用等可靠度分配法、評分分配法等分配方法[1-2]。
文獻[3]以電子元器件為研究對象,提出了面向壽命全過程的可靠性分配方法,使得電子系統(tǒng)在保證壽命末時刻可靠性指標的前提下,各子系統(tǒng)在使用壽命中各個時期的可靠性指標相近。本文借鑒其中的思想與方法,以某重復使用氫氧發(fā)動機為研究對象,開展考慮發(fā)動機在重復使用過程中各個子系統(tǒng)可靠性指標偏差的發(fā)動機系統(tǒng)結構可靠性指標分配,該方法以等可靠度分配為基礎,以重復使用全過程中各子系統(tǒng)結構可靠性的偏差為目標函數(shù),采用遺傳算法進行優(yōu)化,得到最終的結構可靠性分配結果。
1 面向重復使用全過程的可靠性分配方法
1.1 數(shù)學模型
本節(jié)針對由多個子系統(tǒng)串聯(lián)組成的重復使用火箭發(fā)動機系統(tǒng),在均等分配使用壽命末時刻各單元可靠性的基礎上,介紹面向重復使用全過程的結構可靠性分配方法。
考慮一個由N個子系統(tǒng)串聯(lián)組成的復雜系統(tǒng),系統(tǒng)的結構可靠性指標為:使用壽命T時刻末可靠度不小于Rs(T)。采用等可靠度分配法得到第i個子系統(tǒng)T時刻末的可靠度為:
(1)
采用等可靠度分配法可以將壽命末時刻系統(tǒng)可靠性均等分配各個子系統(tǒng),消除了壽命末時刻子系統(tǒng)的“短板”問題,但是由于各子系統(tǒng)的可靠度函數(shù)不同,即使在壽命末時刻各子系統(tǒng)的結構可靠度相同,但在重復使用過程中的某些時刻子系統(tǒng)的可靠度仍存在差異,即仍存在“短板”。為使各個子系統(tǒng)在整個重復使用過程中都具有相近的可靠性水平,在等分配結果的基礎上,引入修正因子Ki(i=1,2,…,N),得[3]:
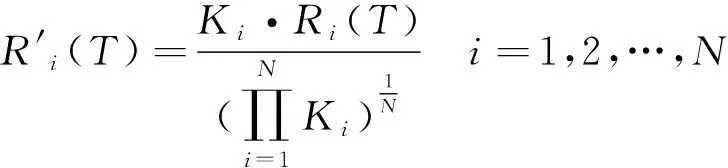
(2)
修正后的系統(tǒng)壽命末時刻的可靠度為:
(3)
1.2 目標函數(shù)
為衡量重復使用過程中各系統(tǒng)可靠度的差異,引入樣本數(shù)據(jù)的方差:
(4)
簡便起見,在重復使用過程中取特定的時刻tj(如tj=0.1T,0.2T,…,0.9T,T)考察各子系統(tǒng)結構可靠度的偏差,定義目標函數(shù):
(5)
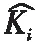
1.3 遺傳算法
遺傳算法是一種基于生物遺傳和進化的自適應概率優(yōu)化算法,最早由美國密執(zhí)安大學的Holland提出[4],現(xiàn)廣泛應用于液體火箭發(fā)動機的優(yōu)化設計中[5-6]。
其基本運算過程如下[4]:
1)初始化,設置進化代數(shù)計數(shù)器t←0;設置最大進化代數(shù)T;隨機生成M個個體作為初始群體P(0);
2)個體評價,計算群體P(t)中各個個體的適應度;
3)選擇運算,將選擇算子作用于群體;
4)交叉運算,將交叉算子作用于群體;
5)變異運算,將變異算子作用于群體,群體P(t)經過選擇、交叉、變異運算之后得到下一代群體P(t+1);
6)終止條件判斷,若t≤T,則t←t+1,轉到2);若t>T,則以進化過程中所得到的具有最大適應度的個體作為最優(yōu)解輸出,終止計算。
2 重復使用發(fā)動機可靠性模型
某重復使用燃氣發(fā)生器循環(huán)的氫氧發(fā)動機由推力室、燃料泵、燃料渦輪、燃氣發(fā)生器、氧化劑泵、氧化劑渦輪、輸運管路等7個子系統(tǒng)組成,如圖 1所示[7]。
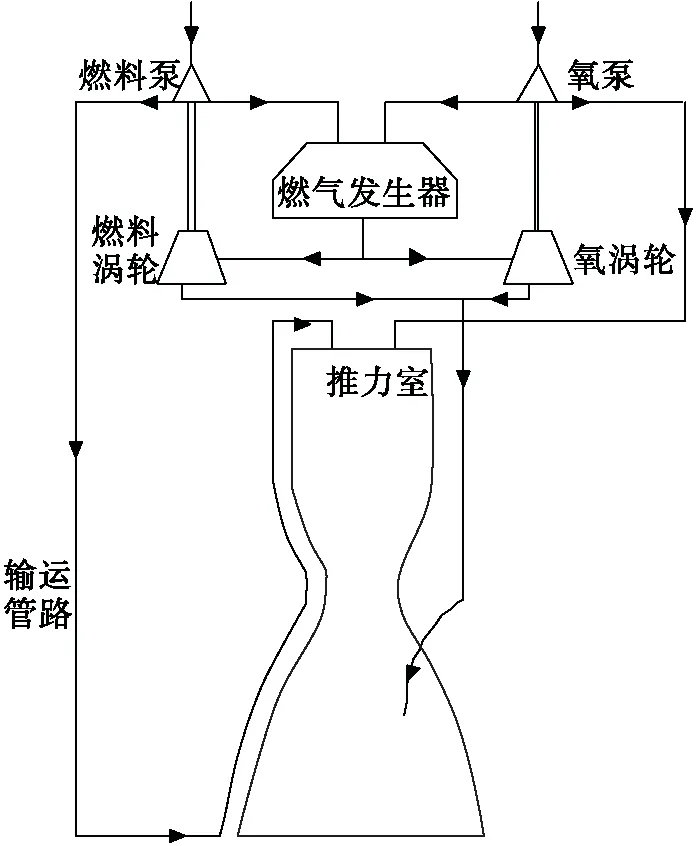
圖 1 燃氣發(fā)生器循環(huán)發(fā)動機系統(tǒng)簡圖Fig. 1 Schematic diagram of liquid rocket engine using gas generator cycle
由于發(fā)動機中任何一個子系統(tǒng)故障都可直接導致整機的故障,故將其看作串聯(lián)系統(tǒng)處理,發(fā)動機系統(tǒng)可靠性為各子系統(tǒng)可靠性的乘積。
液體火箭發(fā)動機其組件的壽命分布均服從二參數(shù)的Weibull分布[1],概率密度函數(shù)為:
f(t|θ,β)
=
(6)
式中:θ為尺度參數(shù);β為形狀參數(shù)。
β一般可根據(jù)工程經驗或者已有的數(shù)據(jù)給出。當β<1時,可用來描述突然故障,當β≥3.25時,威布爾分布與正態(tài)分布相近,僅用來描述漸變故障,當1<β≤3.25時,威布爾分布可描述突然故障與漸變故障的組合[8]。液體火箭發(fā)動機結構復雜,在試車過程中,兩種故障往往一起出現(xiàn)[9],所以本文中β的取值應在1~3.25。
θ也稱特征壽命,是發(fā)動機設計參數(shù)的綜合體現(xiàn)。當β>0.7,θ的值與威布爾分布的平均壽命相近。
威布爾分布的可靠度和平均壽命為[10]:
(7)
(8)
而運輸管路的可靠性一般可近似為1[11]。
3 算例
3.1 原始數(shù)據(jù)
發(fā)動機單次工作時間為180 s,重復使用50次,即總工作時間為9 000 s。發(fā)動機的結構可靠度不低于0.96。即Rs(T)≥0.96。
參考文獻[12]給定各子系統(tǒng)的形狀參數(shù)如表1所示。
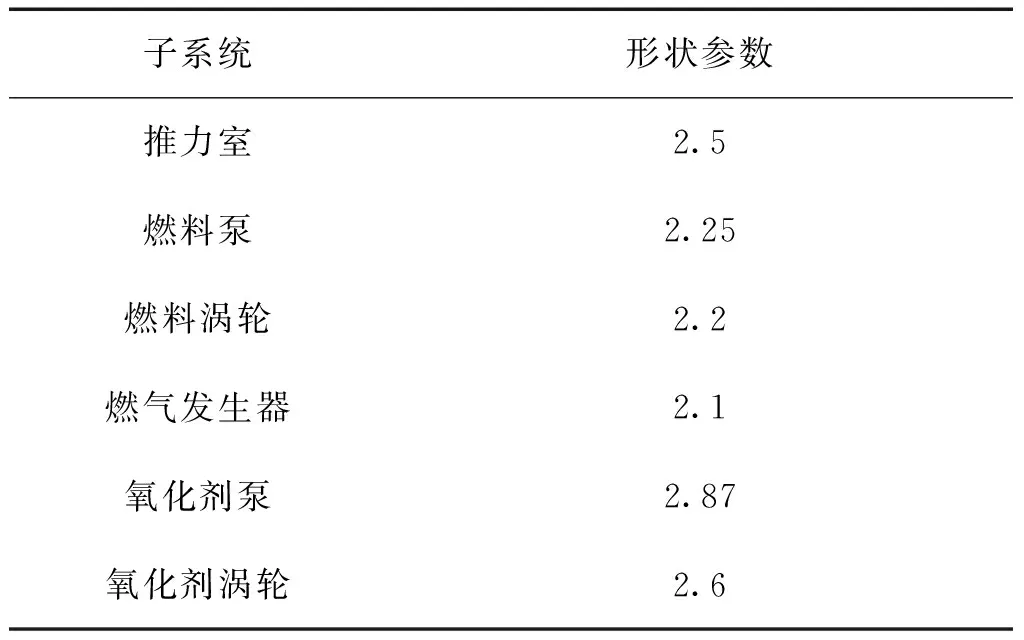
表 1 各子系統(tǒng)形狀參數(shù)
3.2 可靠性分配
按照等分分配原則,得到各子系統(tǒng)在使用壽命末時刻的可靠度為:
(9)
引入修正因子Ki(i=1,2,…,6),得到修正后的各子系統(tǒng)的壽命末時刻可靠度:
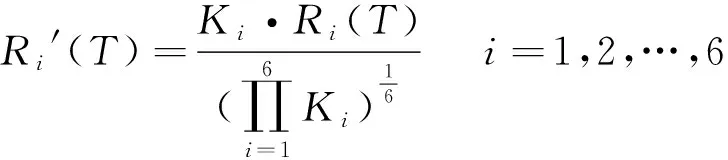
(10)
取發(fā)動機使用壽命全過程中的0.1T,0.2T,…,0.9T,T時刻(即第5,10,…,45,50次使用時)作為可靠度偏差的考核點,得目標函數(shù):
(11)
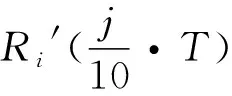
(12)
3.3 分配結果
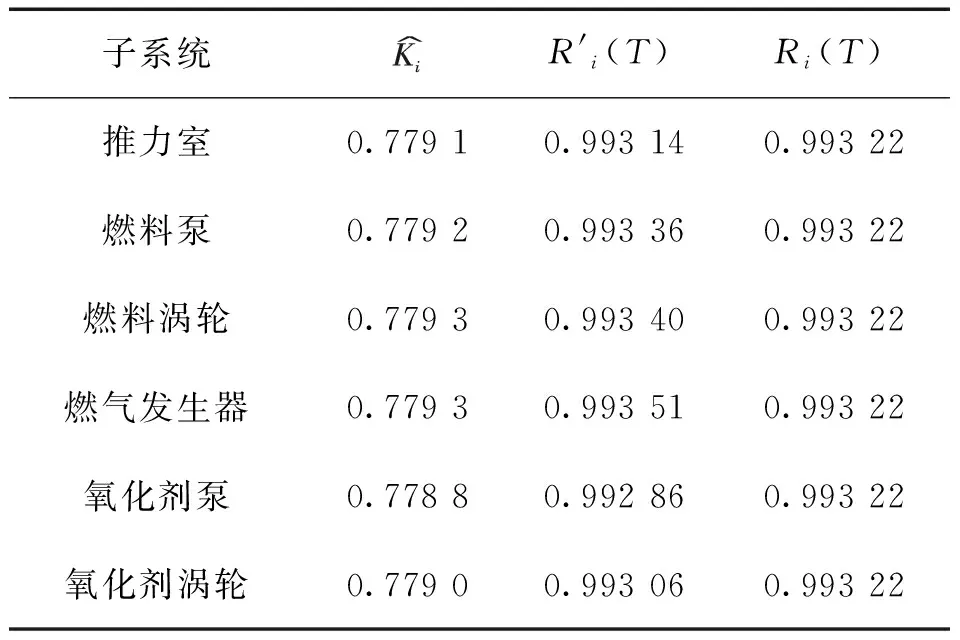
表2 計算結果
進而得到優(yōu)化后各子系統(tǒng)壽命分布函數(shù)中的尺度參數(shù)θp及等分配法得到的尺度參數(shù)θe,如表 3所示。
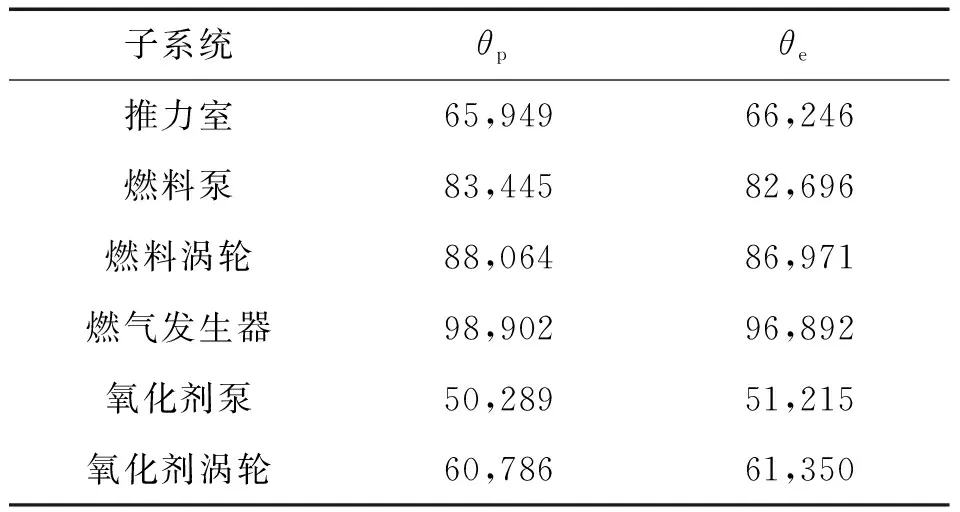
表3 尺度參數(shù)計算結果
圖2和圖3給出了修正前后可靠度隨工作時間的變化曲線,圖4給出了等可靠度分配各考察點子系統(tǒng)可靠度偏差(ED)與修正后各子系統(tǒng)可靠度偏差(PD)。
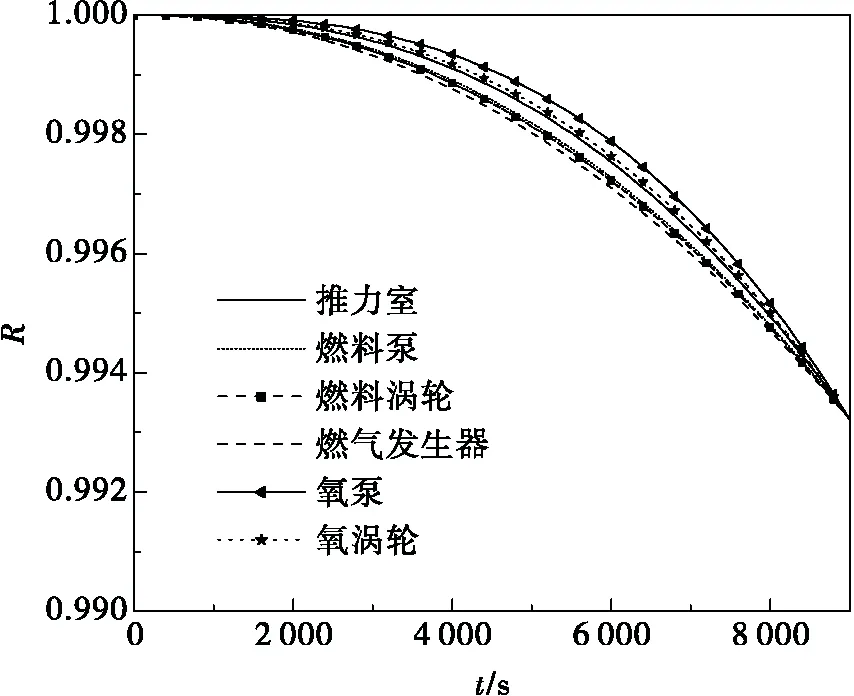
圖 2 可靠度隨時間變化過程(等可靠度分配)Fig. 2 Time-dependent reliability (equal reliability allocation)
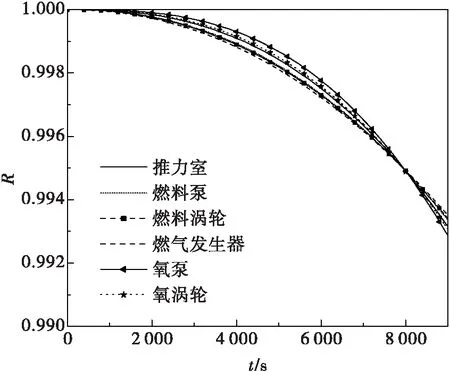
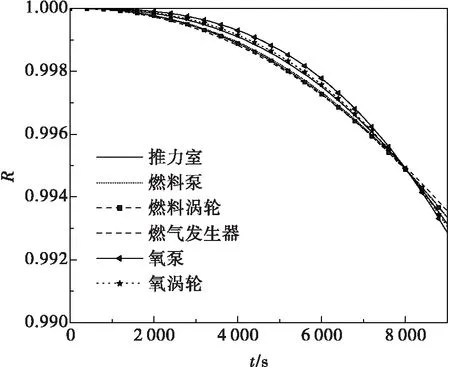
圖3 可靠度隨時間變化過程(優(yōu)化后)Fig. 3 Time-dependent reliability (after optimization)
從圖表中可以看出,經過優(yōu)化后的各子系統(tǒng)可靠度除在使用壽命末時刻外,在其余各考察點的偏差均比等分配法小。從目標函數(shù)的角度看,按照等分配結果計算得到的目標函數(shù)L=3.734×10-7,優(yōu)化后得到的目標函數(shù)L′=2.416×10-7。綜上可知,經過優(yōu)化后的各子系統(tǒng)可靠度在重復使用全過程中的“短板”現(xiàn)象減弱。
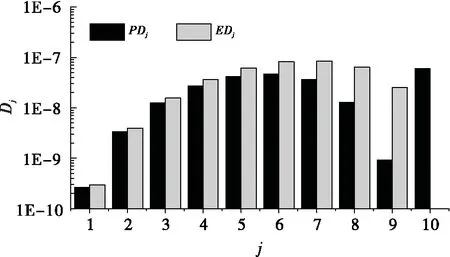
圖 4 考察點各子系統(tǒng)可靠度方差Fig. 4 Reliability variance of each subsystem at check points
3.4 討論
上文在等分配的基礎上以各子系統(tǒng)在任務過程中可靠性的偏差最小為目標函數(shù),對各子系統(tǒng)的可靠度進行分配。在液體火箭發(fā)動機研制過程中,由于各子系統(tǒng)的復雜度、重要度以及環(huán)境條件等不同,實現(xiàn)所要求的可靠度的難易程度也不同,若從成本角度考慮,可以在已有試驗數(shù)據(jù)及專家經驗的基礎上添加約束條件,例如,在使用壽命結束時,限定燃料泵的可靠度要高于燃料渦輪,即:
Rturs(T) (13) 在此限制條件下,得到各子系統(tǒng)在使用壽命結束時刻的可靠度如表4所示。 表4 考慮約束條件的計算結果 圖5 可靠度隨時間變化過程(考慮約束)Fig. 5 Time-dependent reliability (with constraints) 由表4可以看出,添加約束條件后在使用壽命末時刻燃料泵的可靠性為0.993 39,燃料渦輪的可靠性為0.993 38,滿足約束條件。各子系統(tǒng)在使用壽命末時刻的可靠性指標有所調整,目標函數(shù)L″=2.423×10-7,與無約束條件相比,在重復使用中間過程的可靠性偏差總和略有增加,但仍低于等分配計算得到的偏差值。 1)針對采用現(xiàn)有火箭發(fā)動機結構可靠性指標分配方法可能使發(fā)動機在重復使用過程中存在“短板”子系統(tǒng)的問題,以等可靠度分配為基礎,建立面向重復使用全過程的可靠度分配方法。 2)分配結果顯示,相比于等可靠度分配法,該方法在保證發(fā)動機使用末時刻可靠性的同時,使發(fā)動機在工作過程中各子系統(tǒng)的可靠度偏差下降35%。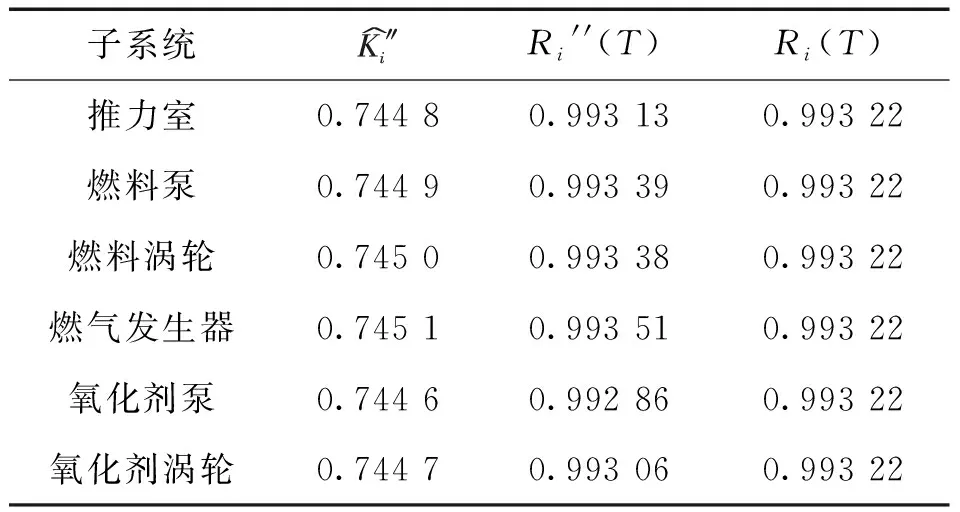
4 結論

