基于卡爾曼濾波的多普勒速度平滑技術研究

張明宇 王艷

（上海船舶電子設備研究所，上海，201108）

在聲學多普勒測速技術領域，隨著水下航行器應用領域的不斷擴大，性能要求的不斷提高，水下導航系統出現了新的發展趨勢，聲學多普勒測速儀已經成為其中重要組成部分，對測速精度提出了更高的要求。在實際的應用中，測速精度主要受到兩方面的影響：測速系統所需要的檢測時延信號在一定程度上受到了水下未知環境噪聲的干擾，導致得到的信號往往存在一定的實際誤差；傳播介質的不均勻性也可能會導致信號出現一定程度上的散射與起伏，致使系統無法對運動物體進行較為精確地測速。

本文通過結合水下航行器載體平臺的特點，基于卡爾曼濾波的系統模型，建立卡爾曼濾波的狀態方程和量測方程，并建立變加速運動模型，使用四種濾波模型對變加速運動進行較為精確的仿真，得到該條件下的最優卡爾曼濾波模型。通過該模型選取最優濾波初值和濾波參數。用實驗中獲得的外場數據對卡爾曼濾波的多普勒測速瞬時速度平滑的有效性進行驗證。

1 卡爾曼濾波的系統模型

卡爾曼濾波技術是在時域上以線性最小方差的準則下的最優估計。其采用遞推算法，核心方程是狀態方程和量測方程[1]。

對于離散時間系統：

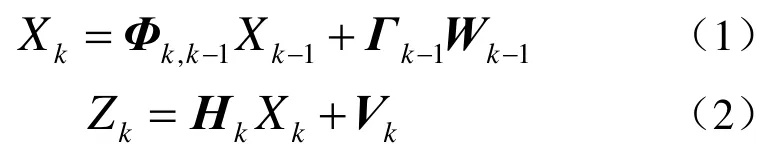
式（1）為狀態方程，式（2）為量測方程。其中，Xk表示第tk時刻的被估計量，Φk,k-1表示第tk-1時刻至第tk時刻之間的一步轉移矩陣，Wk-1表示系統噪聲序列，Γk-1表示系統噪聲驅動陣，Zk表示tk的量測量，Vk表示量測噪聲序列，Hk表示量測陣。

同時，Wk和Vk滿足以下關系：

式中，Qk表示系統噪聲方差陣，Rk表示量測噪聲方差陣，k、j表示不同的時刻。通過簡單的推導，可以得出正確的卡爾曼濾波基本方程[2]：

2 四種濾波模型的性能分析

由于在實際的運動情況中，很難出現物體做加速度恒定的勻速運動或勻加速運動的理想情況，所以本文選擇了加速度變化緩慢的變加速運動模型作為分析討論的對象，并通過CV模型、CA模型、Singer模型以及“當前”統計模型進行性能分析。

2.1 CV模型

CV模型在離散時間條件下，卡爾曼濾波系統的狀態方程為：

式中，xk、vk分別表示物體當前時刻的運的位移與瞬時速度，bk表示加速度的隨機擾動噪聲，且服從于的高斯分布，T表示系統觀測時間之間的間隔時長。

2.2 CA模型

CA模型在離散時間的條件下，卡爾曼濾波系統的狀態方程[3-5]：

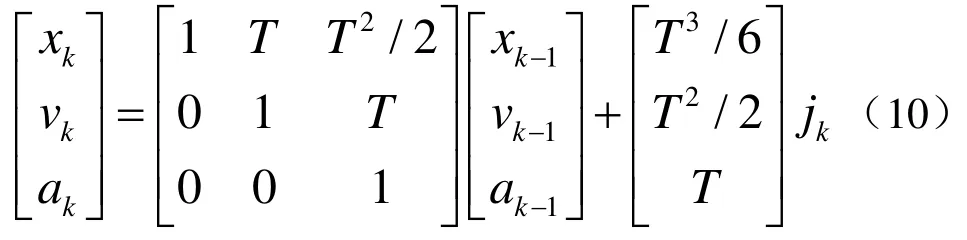
式中，xk、vk、ak分別表示物體當前時刻的位移、瞬時速度與瞬時加速度，jk表示加加速度（急動度）的隨機擾動噪聲，服從的高斯分布，T表示系統觀測時間間隔時長。

2.3 Singer模型

Singer模型在離散時間的條件下，卡爾曼濾波系統的狀態方程[6]：

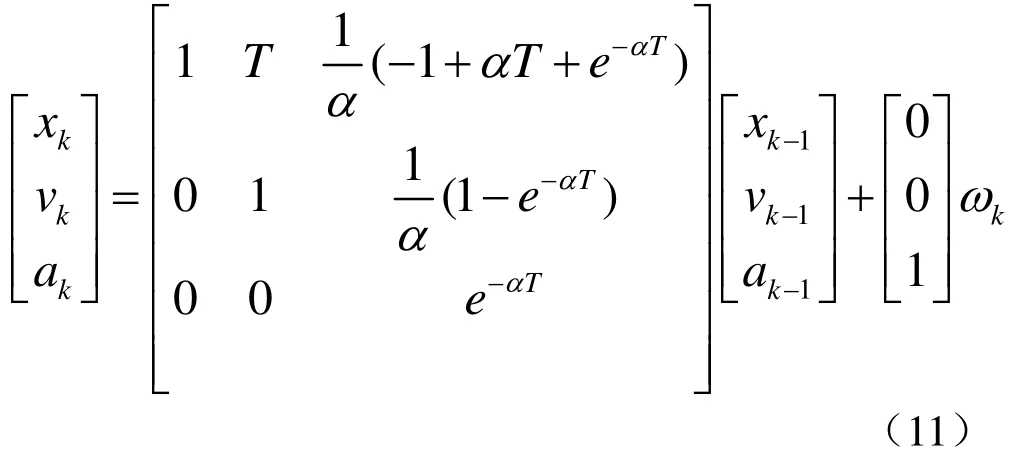
式中，ωk表示服從的高斯白噪聲序列，a為機動頻率。

2.4 “當前”統計模型

“當前”統計模型在離散時間的條件下，卡爾曼濾波系統的狀態方程[7]：

式中，為機動頻率平均值，

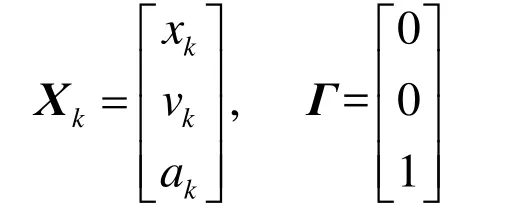
2.5 四種模型濾波的性能仿真分析

把四種濾波模型應用到變加速運動模型中，將濾波結果與真實速度之間的誤差大小作為濾波性能優劣的參考標準，添加服從N(0,10–1)的高斯白噪聲作為量測噪聲，通過時延信息解算物體的速度，作為直接速度信息，進行仿真。

目標零時刻位置為（0 m，0 m），0～200 s內，保持勻速直線運動的運動狀態，在X、Y軸分速度都為10 m/s；在201～400 s內，保持勻速曲線運動的運動狀態，運動半徑設定為1 000 m，線速度設定14 m/s，采樣間隔1 s。

在圖1中，圖（a）顯示了真實軌跡與測速儀測量速度添加噪聲再積分后的軌跡，圖（b）為圖（a）的部分軌跡放大圖，可以較為清晰地看到濾波前的位移和真實位移有一定的差距。觀察后可以發現，測量軌跡與真實軌跡之間存在一定的偏差，這是由于添加了量測噪聲所導致的。圖（c）顯示了經過卡爾曼濾波處理后各模型的軌跡結果，圖（d）為圖（c）的部分放大圖。可以看出，經過卡爾曼濾波后，軌跡上的每個位置都更加接近于真實位置，能夠有效地提高定位精度。

圖1 濾波前后軌跡對比圖

圖2為各模型濾波后的各時刻的速度與真實速度之間的差值。從圖中可以明顯地看出，經過不同模型進行濾波，都會對速度產生一定程度的平滑，即對速度的估計精度在一定程度上提高了。CA模型的濾波效果是最好的。

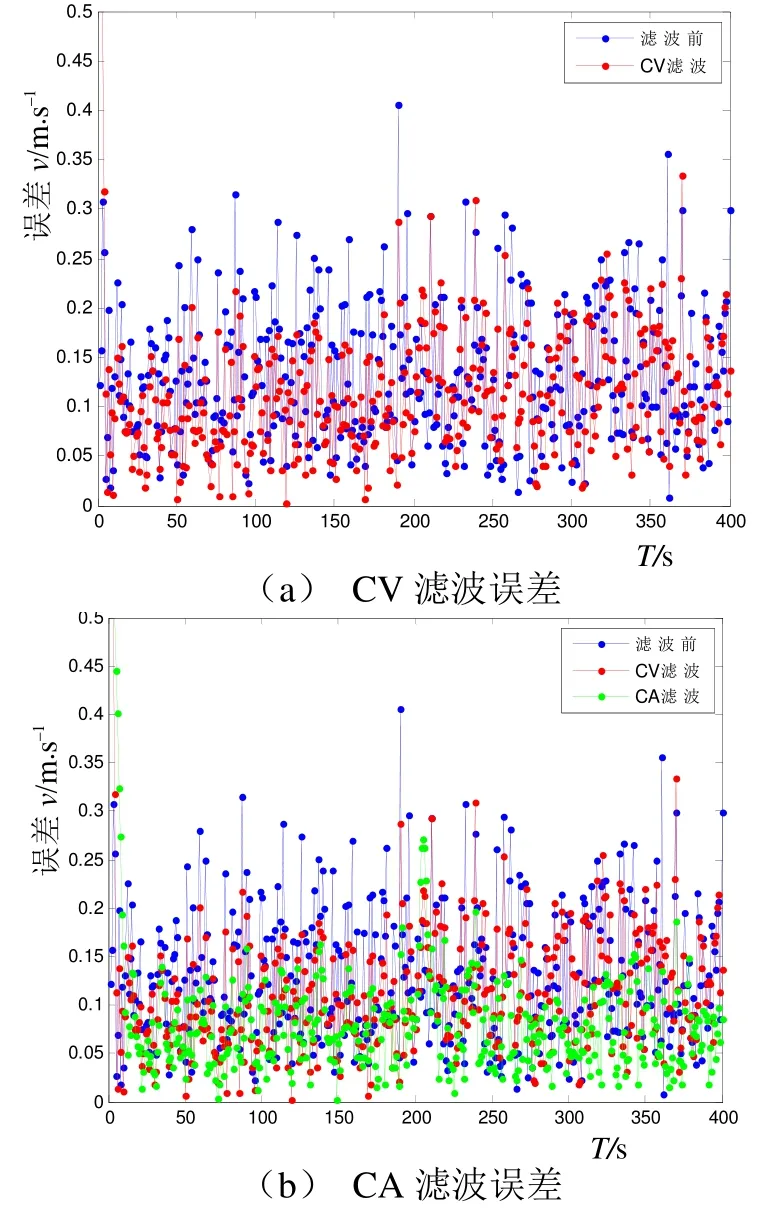
圖2 卡爾曼濾波速度與真實速度之比

綜上，在合理選擇濾波參數的背景條件下，CA模型可以滿足測速精度的需求，完成速度平滑的任務。由于其對運動模型的濾波效果最好，在水下的相關系統具有更廣泛的適用性。所以，選擇CA模型作為系統卡爾曼濾波模型。

3 濾波初值和濾波參數的選取

3.1 濾波初值的選取

卡爾曼濾波是一種遞推算法，初值X0和P0的選取相當重要，要嚴格保證濾波估計是無偏的，方差最小，才能實現較好的濾波效果。為了避免將第一時刻值作為濾波初值所帶來的誤差，選取采樣值的平均值作為初值的方法，更多地利用已有的平均時延數據來計算速度值，并將時延值賦給t0，坐標均值賦給x0，并可以用這些數據來估計初始情況下的協方差矩陣P0，使其在起始階段就有較好的濾波效果，方便操作。

以初始速度0 m/s，加速度0.02 m/s2，添加服從N(0,10–1)的高斯白噪聲作為量測噪聲，沿一個方向作簡單的勻加速直線運動為例進行仿真。從圖3、圖4可以明顯地看出，速度、位移的濾波均出現收斂的情況，且后段差別不大。但在初始階段，平均值的效果非常明顯地優于對方。

圖3 不同初值濾波速度結果

圖4 改變初值后的位移結果

3.2 濾波參數的選取

系統的噪聲方差陣Qk和量測噪聲方差陣Rk兩個參數選取的優劣將會直接地影響著卡爾曼濾波的濾波精度。通常情況下，需要在濾波前通過模擬計算來取Qk和Rk。在機動性不高時，Qk和Rk可以寫作常數q和r。以勻加速運動為例，選取合適的數q和r。水下運動物體的初始位置為(0,0)，X方向初速度0 m/s，加速度0.02 m/s2；Y方向初速度0 m/s，加速度0.02 m/s2，運動時間為500 s，采樣間隔1 s。

3.2.1q值的選取

固定r值，q的取值遞減，從10–6到10–9進行嘗試。從圖5可以明顯地發現，q值的不同取值對效果造成了很大影響，q值選取10–7比較合適。如果q值過大，則效果不明顯，濾波將失去作用；q過小，雖然誤差很小，但當前測量值已經失去了原有的修正作用，隨著運動的進行，可能會出現濾波發散現象。q的取值，應與統計特性相匹配。

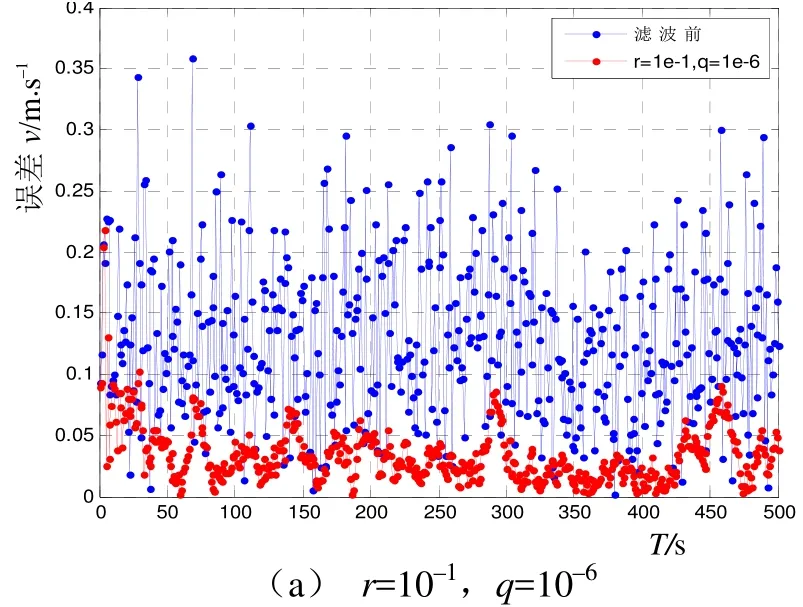
圖5 q對濾波性能的影響

3.2.2r值的選取

固定q值，r的取值遞減，從101～10–2進行嘗試。從圖6可以明顯地發現，r的影響效果同q正好相反。

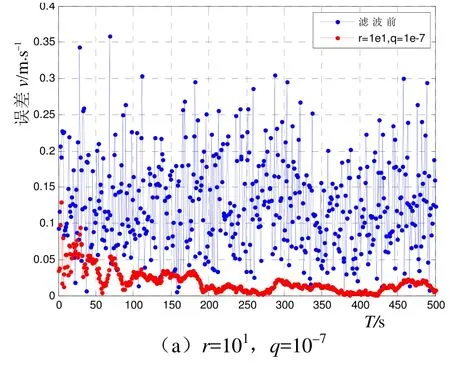
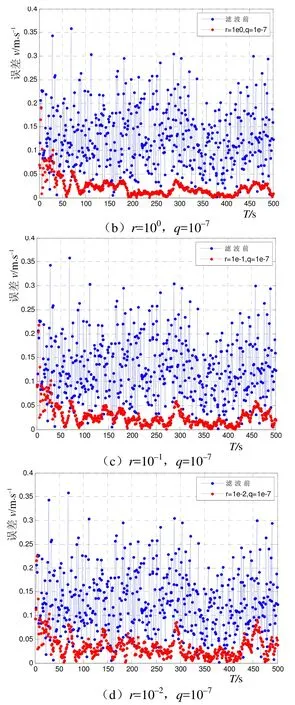
圖6 r對濾波性能的影響

當r取 10–1左右時，濾波的性能達到最好；r較大，當前測量值對濾波值的修正作用比較小，隨時間的累積，可能會出現濾波發散現象；r較小，比較容易引起濾波精度的降低。r選取 10–1比較合適。r的取值，應接近于量測噪聲的情況。

3.2.3q/r對濾波性能的影響

q/r稱為信噪比，選取r=100、q=10–7和r=10–1，q=10–8這兩組參數進行比較。從圖7可以明顯地看出，q/r相同，通過兩組參數進行濾波而得到的濾波效果是較為相同的，不同之處在于初始階段，而r的精確程度，將直接地影響到濾波初始階段的濾波精度以及誤差的收斂速度，r越準確越好。

圖7 q/r對性能的影響

4 試驗數據驗證

圖8為運動物體在外場運動5 000 s、采樣間隔為1 s時，多普勒測速儀測得的速度隨時間變化的觀測數據。通過第2節和第3節分析，采取CA模型作為濾波模型，為簡便起見，選取濾波的初值速度為0 m/s，濾波參數r=10–1、q=10–7進行卡爾曼濾波。從圖9和圖10可以看出，測得的速度得到了相當大程度的平滑。

假設某一時刻的真實速度是當前時刻測量值與前后20個時刻的測量速度的平均值，將此真實值與濾波前及CA濾波后的值進行比較即可得到誤差的大小。代入外場試驗數據進行驗證，通過CA模型進行濾波，從圖11與圖12可以看出，速度誤差明顯減小，證明卡爾曼濾波方法對多普勒速度平滑工作是有效的。

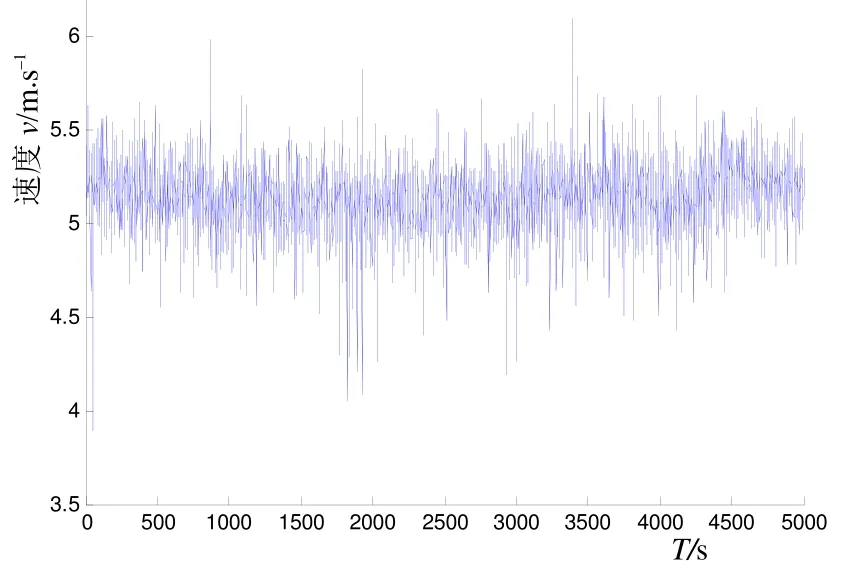
圖8 測速儀測得的速度

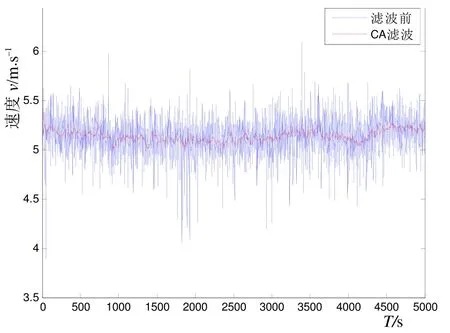
圖9 速度平滑效果

圖10 部分時刻速度平滑效果比較

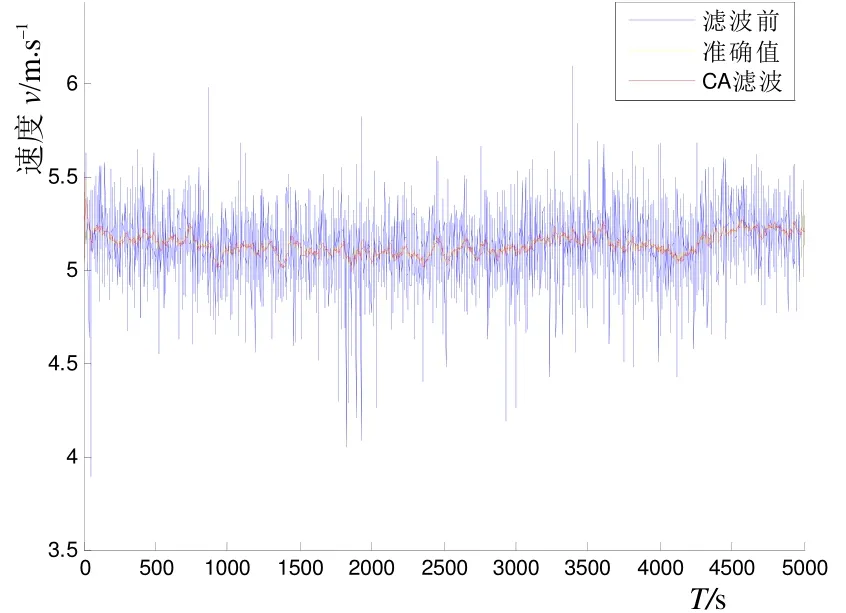
圖11 速度平滑效果比較

圖12 測量值與CA濾波和真實值之間的誤差

5 結論

工程中使用多普勒測速儀進行測速時，測速結果出現誤差是不可避免的，選擇合適的方法，對多普勒速度進行平滑就顯得尤為重要。通過卡爾曼濾波對速度進行平滑而得到較為精確的速度值，對運動物體的定位及航跡推算有著一定的幫助及實用價值。在本文研究中，對濾波參數的選取建立在對已有文獻的研究上，缺少系統的理論支撐，需要進行下一步的研究。以前的卡爾曼濾波更多地是針對位移進行研究，本文則是建立在速度平滑的基礎上，對航跡等數據作進一步的推算。本文通過使用卡爾曼濾波方法，并選取合適的參數，對速度進行平滑，可以對定位起到幫助，對航跡推算也有一定作用。