多元IV型彎張換能器半波長布陣仿真研究

陳立綱 馬振

（1.海軍駐杭州地區軍事代表室，杭州，310023；2.第七一五研究所，杭州，310023）

IV型彎張換能器由驅動振子、振動殼體等部件組成。換能器工作時振子的伸張、收縮驅動殼體的彎曲振動并進行聲輻射。IV型彎張換能器具有低頻、大功率、小尺寸的特點（典型的IV型彎張換能器最大線性尺寸約為諧振波長的1/4），主要工作于0.3～3 kHz頻率范圍。為了滿足聲源級和指向性的要求，換能器常需要組成陣列工作。成陣的方式有半波長布陣和密排布陣等。其中半波長布陣是指相鄰兩個換能器聲中心間距等于諧振處波長的一半。半波長布陣的主瓣聲源級高，無柵瓣。對于IV型彎張這類低頻換能器而言，半波長布陣情況時，有限元模型需要更大的聲場。本文分析了聲場尺寸對換能器性能的影響，并推導了聲場應滿足的尺寸要求。

1 單個IV型彎張換能器仿真

換能器成陣前首先應確定單個換能器性能。單個IV型彎張換能器殼體長軸為250 mm、短軸為130 mm、高為100 mm、厚度為15 mm。結構如圖1所示。利用Comsol有限元軟件建模如圖2，其中有限元水域半徑為2 m，外側設置球面波擴展模擬無限大水域，進行水中諧響應仿真并提取相關結果見圖3～圖5。

圖1 彎張換能器模型

圖2 水中有限元模型

圖3 長軸方向發送電壓響應

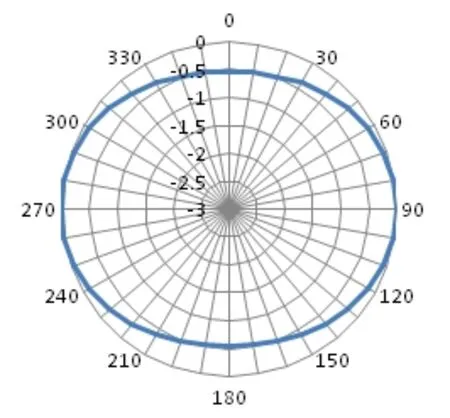
圖4 長軸-高度平面指向性

圖5 長軸-短軸平面指向性

仿真顯示單個換能器諧振頻率約為1.8 kHz，長軸發送電壓響應約為141.5 dB。從指向性圖上可以看出，長軸-高度平面換能器響應最大起伏為0.5 dB（其中0°為高度方向，90°為長軸方向）；長軸-短軸方向最大響應起伏為3 dB（其中0°為長軸方向，90°為短軸方向）。可以看出，換能器響應在空間上起伏較小，尤其是長軸-高度平面可近似看做無指向性。

2 兩種方法計算半波長布陣性能

針對 IV型彎張換能器短軸方向響應較小的特點，將換能器沿短軸方向半波長布陣。分別布2元、4元、6元、8元、10元陣，并用經典理論和有限元計算響應與指向性性能。

2.1 經典理論計算

沿短軸方向布陣，單個換能器布陣方向上最大尺寸（短軸長度）約為波長的1/6，換能器尺寸遠小于諧振時波長，換能器空間上響應起伏較小，因此可以用經典半波長布陣計算公式估算陣列的響應與指向性。公式如下[1]。

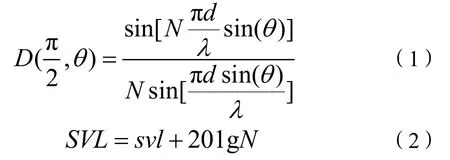
式（1）為半波長線陣的指向性計算公式，式（2）是半波長布陣情況下陣列發送電壓響應計算公式。其中N為陣元個數，d為布陣間距（這里取波長的一半），λ是諧振時波長（這里取1.8 kHz為諧振頻率），svl是單個換能器發送電壓響應，SVL是陣列的發送電壓響應，D（π/2,θ）是陣列高度方向（換能器短軸-高度所在平面）上指向性，其中θ=0為過陣列聲中心垂直于線陣的方向。計算響應隨陣元個數變化的結果見表1。計算高度方向指向性結果見圖6和表2。從表1可以看出隨著陣元個數的增加，陣列的發送電壓響應逐漸增高；從圖6和表2可以看出，半波長布陣情況下陣列無柵瓣，旁瓣級逐漸降低，–3 dB波束寬度逐漸減小。

表1 不同陣元數下的響應

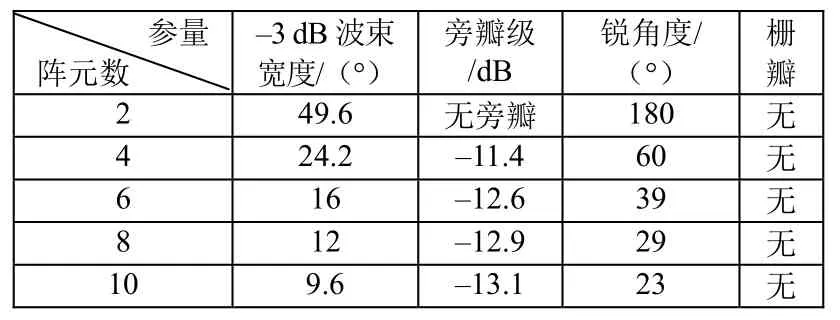
表2 不同陣元的指向性參數

圖6 高度方向指向性

2.2 有限元建模分析

沿短軸方向布陣，分別建立2元、4元、6元、8元、10元陣列模型。布陣間距為1/2波長（1.8 kHz頻率處），有限元水域半徑為3 m，水域外側設置球面波擴展模擬無限大水域。其中十元陣的 1/8模型如圖7。分別計算2元、4元、6元、8元、10元陣列的發送電壓響應和指向性結果見表3、表4和圖8。

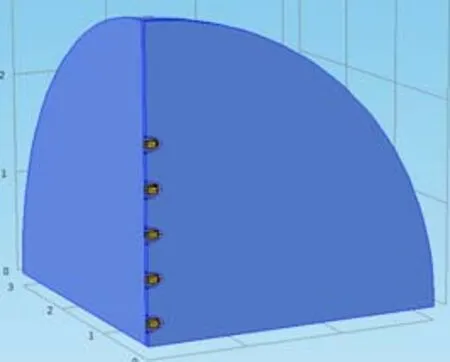
圖7 十元陣有限元模型

表3 不同陣元的發送電壓響應

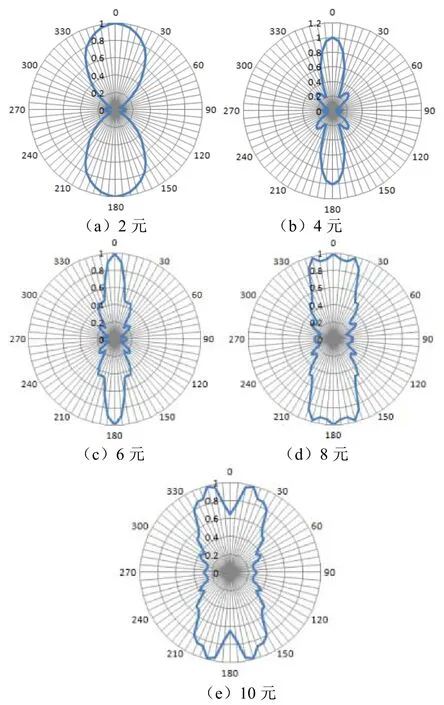
圖8 高度方向指向性

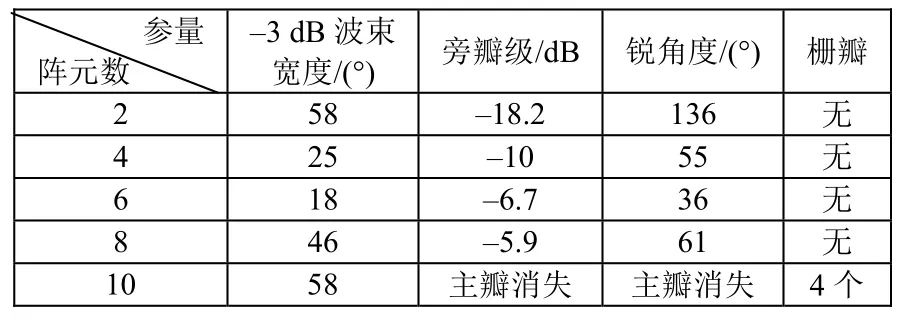
表4 不同陣元的指向性參數

從仿真數據可以看出，隨著陣元個數的增加陣列發送電壓響應先增大（2元～6元）后減小（6元～10元）；從指向性圖可以看出，從6元～8元，陣列主瓣逐漸變得平坦，10元陣列的主瓣位置出現凹谷，凹谷兩邊出現四個柵瓣。

2.3 對比分析

對比兩種方法計算的響應如圖9。從圖中可以看出，理論計算的響應結果隨陣元數的增加而增大，有限元計算的響應隨陣元數的增加而先增大（2元～6元）后減小（6元～10元）。理論計算的響應值要大于有限元計算的響應值，并且二者差值隨陣元數的增加而逐漸增加。另外應當注意的是在 2元、4元時，理論計算值與有限元計算值比較相近。

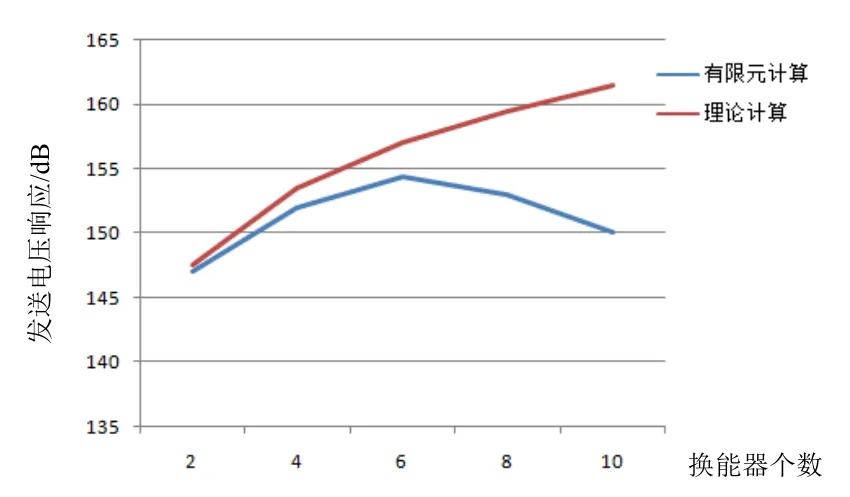
圖9 兩種方式計算響應對比

通過對比可以看出兩種計算方法在計算2元、4元、6元的指向性的結果相近，8元、10元的計算結果相差很大。其中從6元～8元的–3 dB波束寬度反而增大以及10元陣0°、180°方向出現凹谷這兩種現象與實際工程經驗相違背。

綜上可以得出，在本例的模型條件下，隨著陣元數的增加，有限元仿真結果與經典理論計算結果的差別越來越大。

3 現象解釋與聲場尺寸計算

3.1 現象解釋

利用經典理論公式計算陣列的性能時需滿足“點源”和“基元間隔”兩個條件[1]。本例中的IV型彎張換能器基本滿足上述條件，所以用經典理論計算的結果應與實際測試結果相接近。但有限元計算結果與經典理論相差較大，并且這種差別隨陣元個數的增加而變大，這種現象的主要原因是有限元模型中水域尺寸較小，不能滿足計算發送電壓響應和指向性的聲場條件。解釋如圖10。

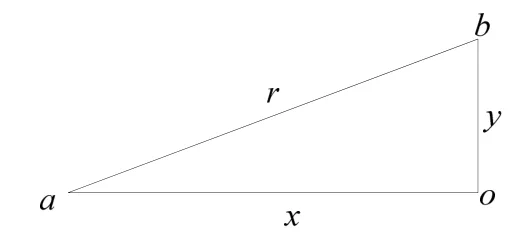
圖10 兩種方式計算響應對比

圖10中o點為聲中心，a為觀測點，b為陣列中任意陣元聲中心，其中觀測點距聲中心的距離為x，陣元聲中心距陣列聲中心距離為y，陣元聲中心距觀測點距離為r，r=sqrt(x2+y2)。可以計算出各陣元到觀測點（x=3 m）與聲中心到觀測點的聲程差見表5。

表5 不同聲中心下的聲程差計算表

為了解釋聲程差對觀測點響應的影響，這里記觀測點處接收到的不同陣元的聲壓之和為：

式中P為總聲壓，w為角頻率，k為波數，xn為聲程差。ej(wt-kx)為接收中心點的聲壓（實際陣列中可能不存在，此處為了解釋簡單而引入）；ej(wt-k(x+xn))為接收到與中心點聲程差為xn的陣元的聲壓。為了簡化計算，上式中忽略陣元與接收點距離對聲壓的幅值影響，可改寫為：

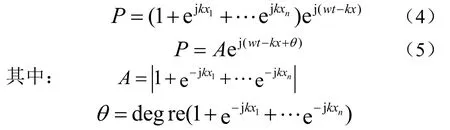
為了簡化計算，這里僅取X1進行分析。

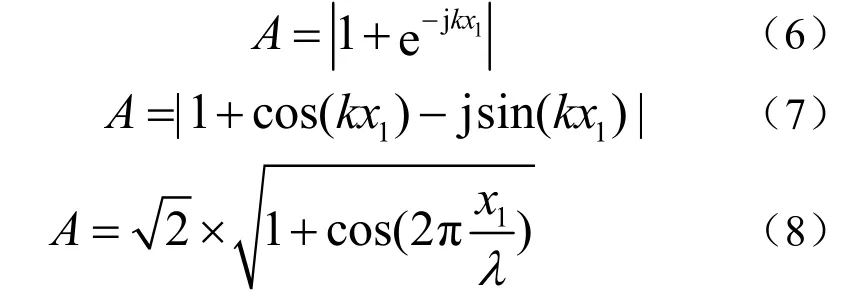
上式中k=2π/λ，其中λ是諧振波長。可以看出，當x1＜λ/4 時二者正相疊加；當λ/4＜x1＜3λ/4 時二者反相疊加；當λ3/4＜x1＜λ時二者正相疊加。對于本例中的陣列，從2元陣到10元陣，陣元聲程差逐漸增大，其中2元～6元陣列的聲程差小于λ/4，8元、10元的聲程差大于λ/4小于3λ/4。所以從2元～6元，觀測點的響應逐漸增大，但由于聲程差逐漸變大，有限元計算的響應值與經典理論的計算值差別隨陣元數的增加而增大；從8元～10元，聲場反相疊加，觀測點的響應逐漸減小，并且在指向性圖上逐漸出現凹谷。

3.2 聲場尺寸計算

用有限元軟件計算陣列響應與指向性時聲場尺寸也應滿足遠場條件，即任意兩陣元到中心觀測點的聲壓的幅值與相位均相同（聲線平行）[2]。這一條件可轉換為距聲中心最遠的陣元到觀測點與聲中心至觀測點的聲程差小于1/4波長：

當聲程差取為1/4波長的1/10時，可計算自由場水域尺寸為：

對于半波長布陣，諧振頻率為1.8 kHz的換能器的線陣，可求出不同陣元數下自由場水域尺寸，見表6。

表6 不同陣元數下聲場尺寸

針對上述結果分別對2元與4元陣進行仿真分析，圖11、圖12為響應隨水域半徑增大的變化。

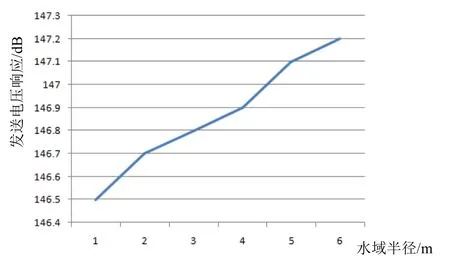
圖11 2元陣響應隨水域半徑變化

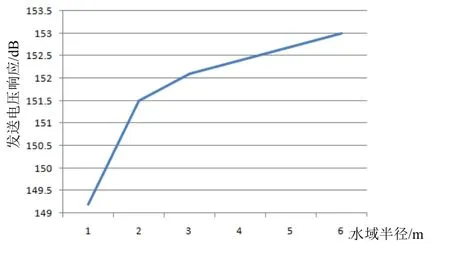
圖12 4元陣響應隨水域半徑變化

從圖中可以看出，對于2元陣，隨著水域尺寸從1 m變大到6 m，響應從146.5 dB增加到147.2 dB，并逐漸趨近于理論計算值147.5 dB；對于4元陣，隨著水域尺寸從1 m變大到6 m，響應從149.2 dB增大到153 dB，也逐漸趨近于理論計算值153.5 dB。2元陣在水域尺寸為1 m的情況下響應值與理論計算仍有約1 dB的差別，這主要是因為換能器尺寸相對于聲場尺寸過大，不能看做點源。綜上可以看出，用有限元對陣列進行仿真時，聲場尺寸對陣列的響應與指向性均有較大影響，為了獲得較為準確的計算結果，聲場尺寸應滿足一定的尺寸條件。

4 總結

本文通過對比經典理論和有限元仿真，分析了有限元水域尺寸對仿真數據的影響，解釋了水域尺寸影響仿真結果的機理，并在此基礎上推導出陣列仿真時水域應滿足的尺寸要求。需要說明的是本文中選取的遠場條件為四分之一波長的 1/10，在實際建模中應根據計算量和計算精度選取合適的遠場條件。另外在陣元數較多，模型較大的情況下，可以使用有限元與邊界元相結合的方式減小計算量。