超聲波甘草酸提取動力學模型

廖建慶，王涵，王咸鵬，袁志強

?

超聲波甘草酸提取動力學模型

廖建慶1，王涵1，王咸鵬2，袁志強1

(1. 宜春學院物理科學與工程技術學院，江西宜春 336000；2. 海南大學南海海洋資源利用國家重點實驗室，海南海口 570228)

為超聲波甘草酸的提取提供理論依據，以超聲波強化機理為基礎，對現有的中草藥浸取動力學方程進行改進，提出了一種含超聲功率、超聲頻率和提取溫度的超聲波動力學模型。采用Origin7.5軟件中的功能模型來預測動力學模型參數即甘草酸平衡濃度和提取速率系數，建立了用于預測甘草酸濃度隨超聲功率、超聲頻率、提取溫度和時間變化的動力學模型。數值仿真結果顯示，模型預測的最大相對誤差僅為8.74%，表明建立的動力學模型具有較好的擬合度，因此對超聲波甘草酸提取工業具有一定的理論參考價值。

超聲波；甘草酸；動力學模型；提取

0 引言

甘草，又名甜草、密甘等。廣泛分布在我國的大部分地區，是一種常見的藥用價值極高的中草藥之一。傳統上甘草用于治療消化性潰瘍、哮喘、咽炎、瘧疾、腹部疼痛、失眠、感染等疾病。甘草的成分包括甘草酸、類黃酮、異黃酮、查耳酮、香豆素、三萜類化合物等，其中甘草酸是甘草的最主要的活性成分，在臨床上可用于降血壓、止咳平喘、抗變態反應、抗腫瘤、抗過敏、抗溶血、抗炎癥等。除了藥用作用外，在藥物制劑中，甘草也被廣泛用作煙草、食品和糖果中的甜味劑或功能性添加劑產品。

由于對甘草的提取屬于一種固液提取過程，因此傳統的提取方法主要采用溶劑提取法[1]、索氏提取法[2]、微波提取法[3]等，這些方法未通過模型預測對甘草酸的萃取率進行預測，因此，通過建立動力學模型對甘草酸得率在生產和利用方面都具有非常重要的理論價值和現實意義。通常Peleg模型、非穩態擴散模型、傳質動力學模型是其采用的主要提取動力學形式[4-7]，然而這些動力學模型都具有一定的局限性，比如只針對某個單變量隨提取時間的變化進行討論，針對多個變量隨提取時間對甘草酸的影響研究還很少，尤其將超聲頻率隨同超聲功率和提取溫度作為主要變量而建立的動力學模型還鮮見報道。

因此，以超聲波強化機理為基礎，采用Fick定律，對現有推導出的超聲提取動力學模型進行改進，探討了超聲功率、超聲頻率和溫度對甘草酸的提取的影響，建立了包含超聲頻率在內的關于甘草酸濃度與提取變量隨提取時間之間的動力學模型，為超聲波甘草酸提取工業提供理論依據。

1 超聲提取過程動力學模型

在中草藥浸取過程中，儲茂泉等[8]在非穩定擴散條件下定義了濃度梯度為時間的冪函數，并以此對Fick第一擴散定律進行了修正，建立了中草藥提取過程的動力學方程：

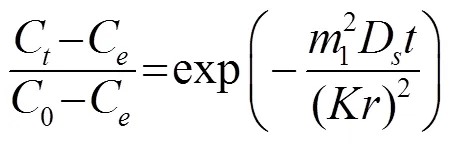
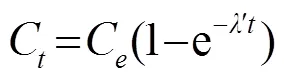
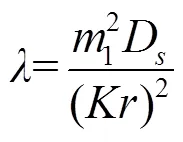
在超聲波強化天然物提取過程中，超聲波強化機理是通過提高渦流擴散系數來增加提取物所有的分子擴散系數，因此，提取過程的擴散速度隨著分子擴散系數的增加而加快[9]。因此，擴散系數可以認為是分子擴散系數和渦流擴散系數之和，即

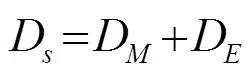
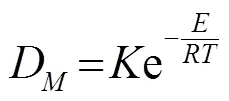
其中，表示擴散活化能，表示提取溫度，表示摩爾氣體常數。由于超聲波強化機理會同時產生空化效應和機械效應，這些強化效應除了主要跟超聲功率和提取溫度有關外，還跟超聲頻率、功率等因素有關[10-11]，因此將渦流擴散系數表示為

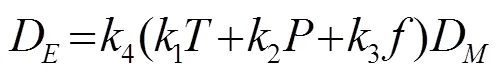
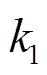
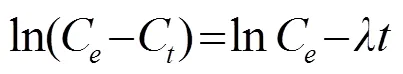
或

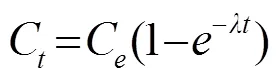
2 實驗

2.1 材料與儀器

甘草片購于南昌中藥材市場，70%乙醇，氯仿，氨水，鹽酸，無水乙醇，重蒸餾水(自制)，甘草酸標準品。

20～100 kHz槽式、頻率和功率可調的超聲波處理系統(北京市金星超聲設備有限公司)；We10-1型電熱鼓風箱(上海市第二五金合作工廠)；721A型分光光度計(四川儀表廠)；FZ-102型植物試樣粉碎機(天津市日用五金制品八廠)；JA2003分析天平(上海分析天平儀器廠)；高速離心機(日立CF16Rx)；SHZ-3型水循環真空泵(上海比朗儀器有限公司)。

2.2 實驗方法及分析

本實驗甘草酸的提取采用超聲波提取法，試驗設計、繪制標準曲線的方法以及統計分析的方法和提取產物甘草酸得率的測定和計算見文獻[12]。

3 結果與分析

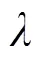
3.1 超聲功率動力學模型

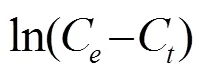
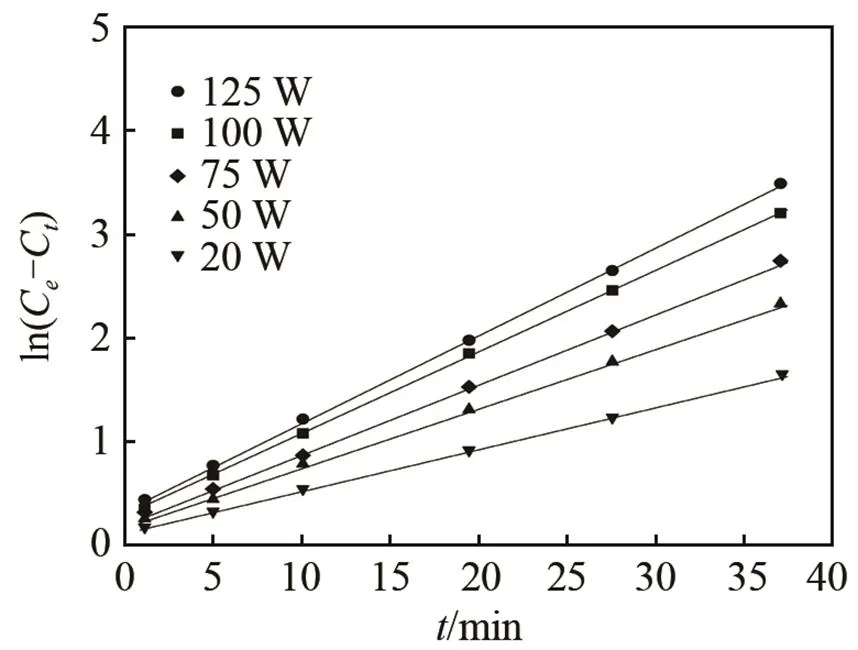
圖1 超聲功率變化條件下的ln(Ce-Ct)與時間t關系

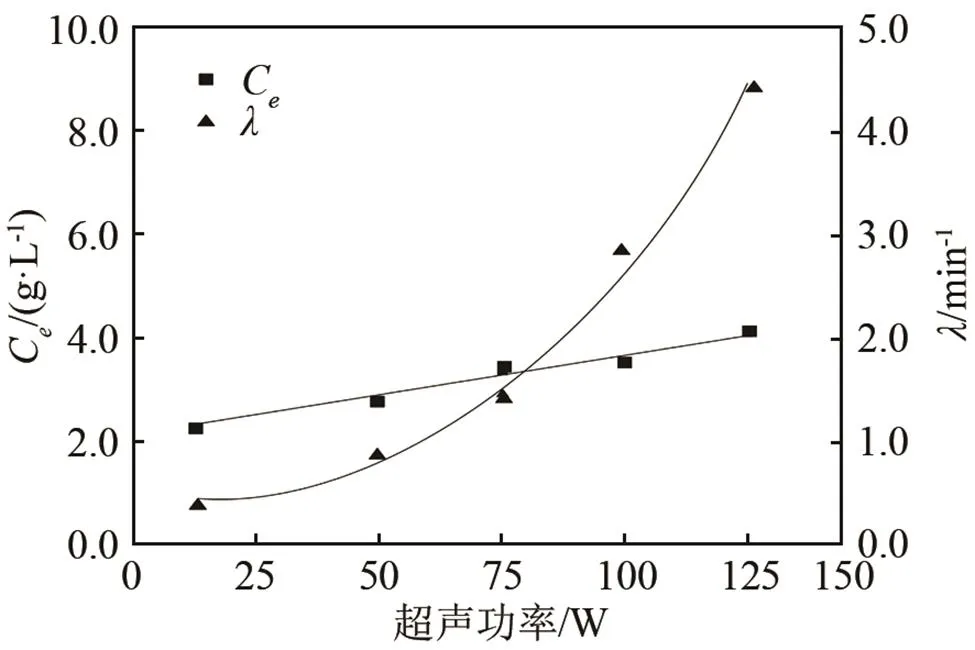
圖2 超聲功率變化時的甘草酸平衡濃度(Ce)和提取速率系數(λ)

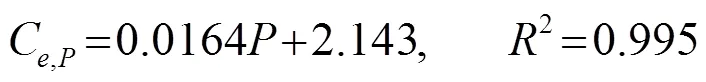
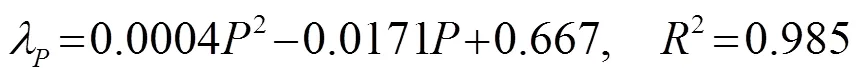
由式(8)、(9)和式(10)通過代換計算可以得到甘草酸提取動力學模型，在超聲功率變化的條件下可以得到：

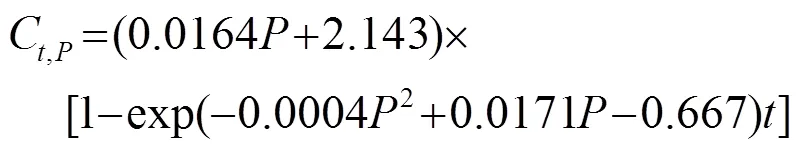
式(11)表示在70%的乙醇溶液、提取溫度為35℃、超聲頻率為55 kHz和料液比為1:30 (v: w)的條件下超聲功率變化的動力學模型，通過該模型可以預測在超聲功率變化的情況下甘草酸提取過程對萃取率的影響。

3.2 超聲頻率動力學模型

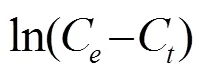
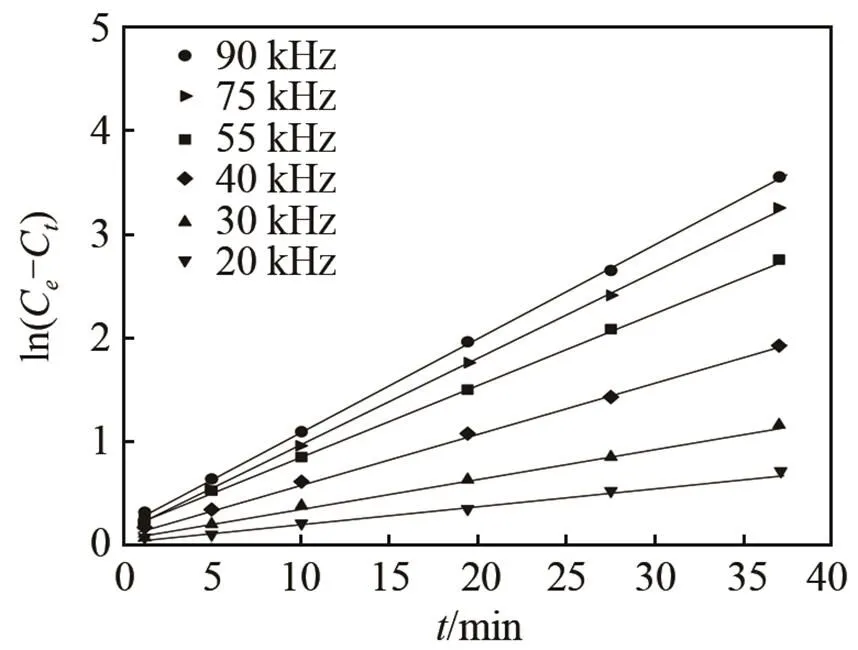
圖3 超聲頻率變化時的ln(Ce-Ct)與時間t關系

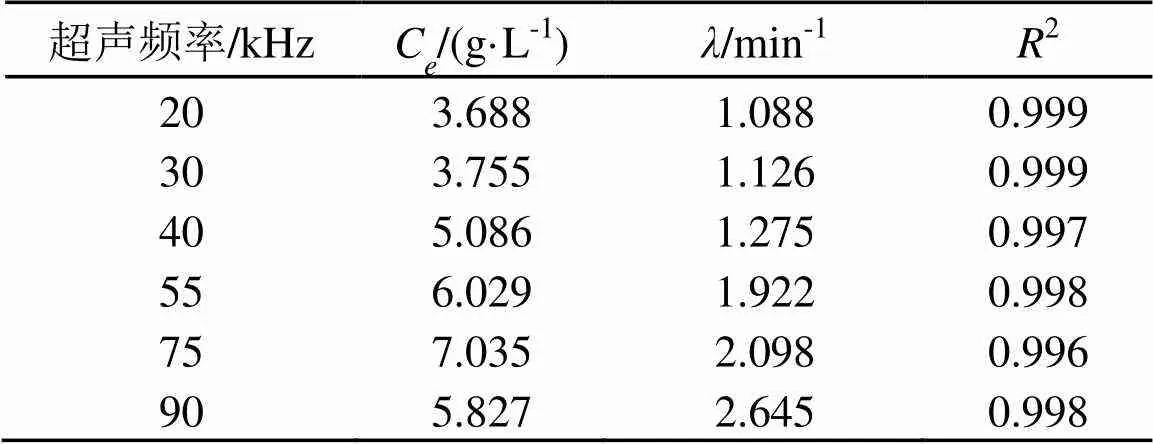
表2 超聲頻率變化時甘草酸提取動力學模型參數

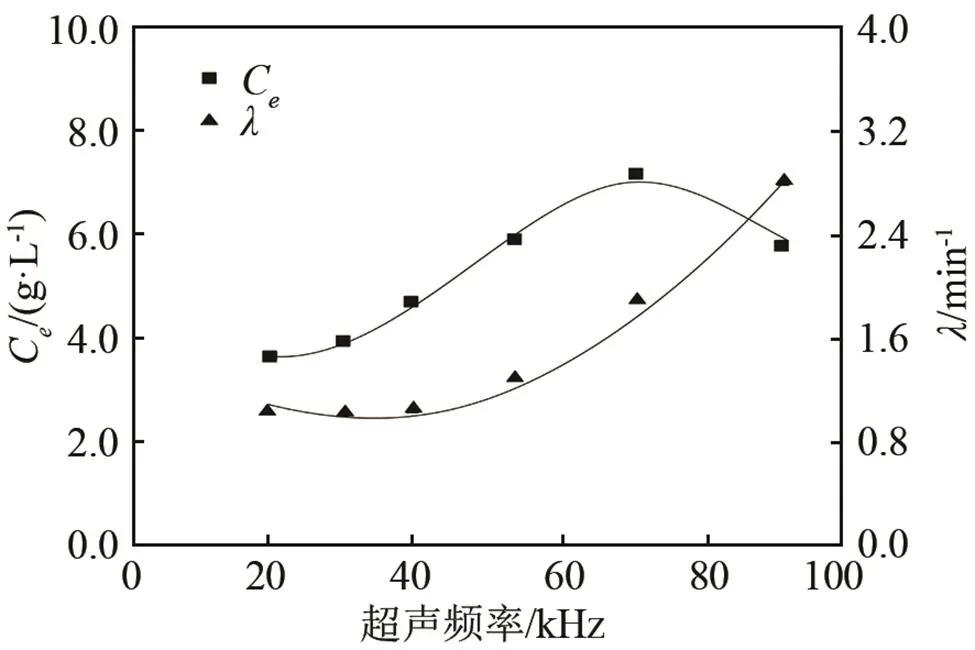
圖4 超聲頻率變化時的甘草酸平衡濃度(Ce)和提取速率系數(λ)

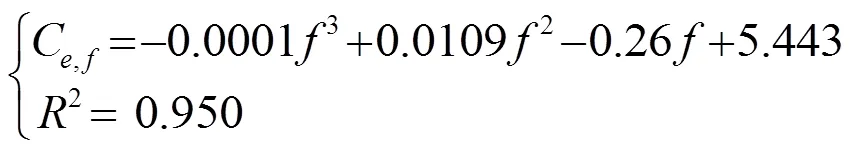
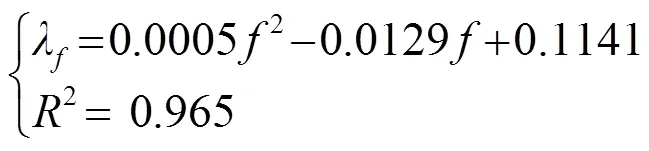
將式(12)、(13)分別代入式(8)，則甘草酸濃度的提取動力學模型在超聲頻率下為

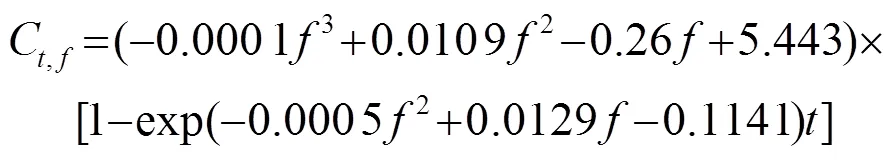
式(14)表明，在70%的乙醇溶液、超聲功率為125 W、提取溫度為35℃和料液比為1: 30 (v: w)時，超聲頻率變化的動力學模型，通過該模型可以預測在超聲頻率變化時甘草酸提取過程對產率的影響。

3.3 提取溫度動力學模型

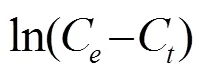
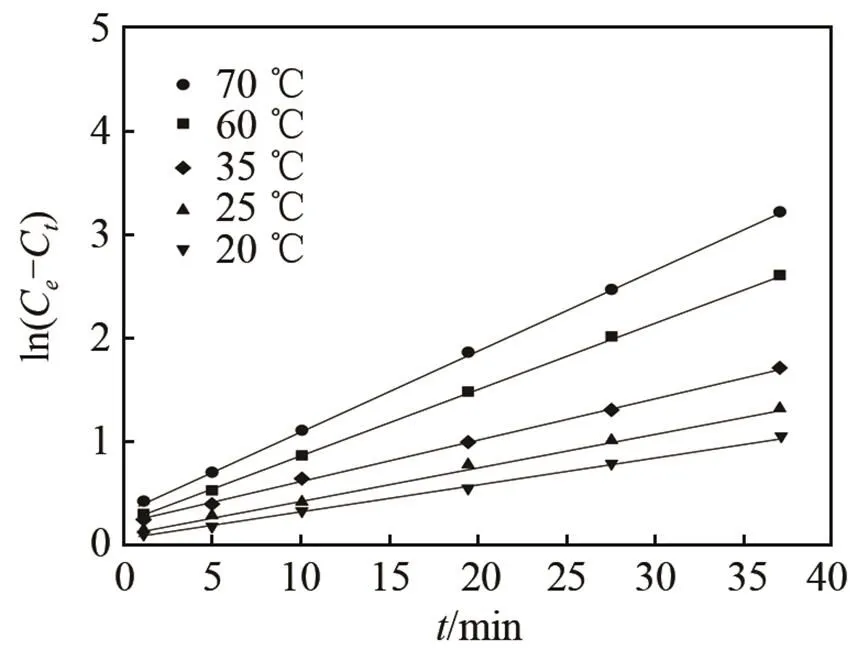
圖5 提取溫度變化時的ln(Ce-Ct)與時間t關系

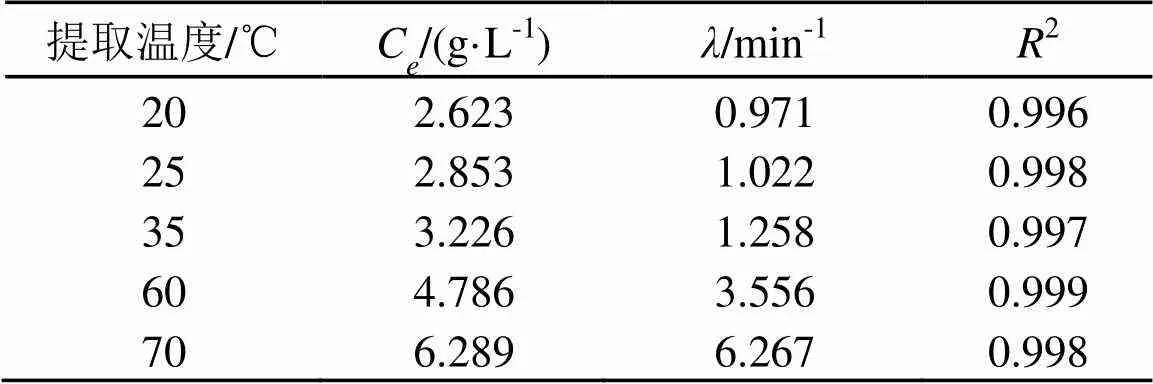
表3 提取溫度變化時甘草酸提取動力學模型參數

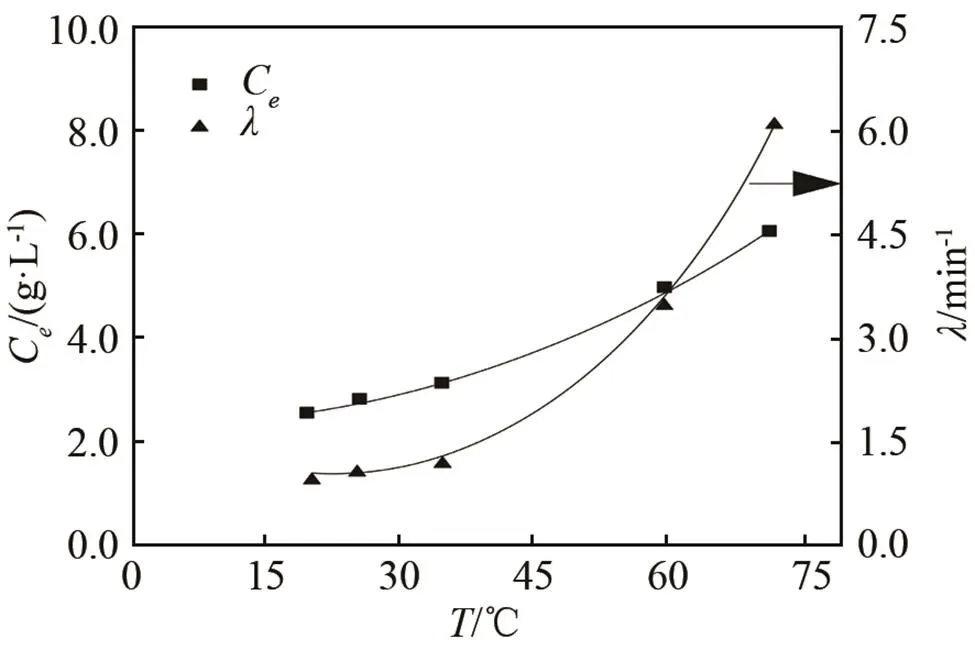
圖6 在不同提取溫度下的甘草酸平衡濃度(Ce)和提取速率系數(λ)

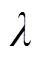
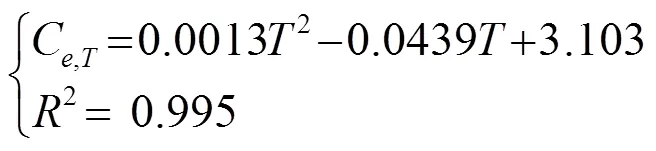
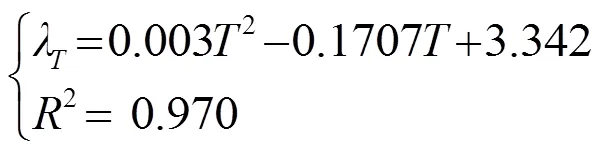
將式(15)、(16)分別代入式(8)，則在提取溫度時，提取甘草酸的動力學模型方程為

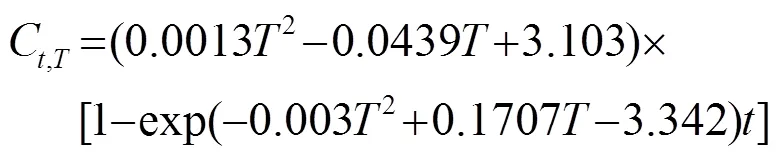
式(17)表示在70%的乙醇溶液、提取溫度為35℃、超聲功率為125W、超聲頻率為55 kHz和料液比為1:30 (v: w)條件下提取溫度變化的動力學模型，通過該模型可以預測在提取溫度變化的情況下甘草酸提取過程對萃取率的影響。

4 數值仿真及驗證

為進一步驗證本文所構建的關于甘草酸提取過程中超聲功率動力學模型、超聲頻率動力學模型和提取溫度動力學模型的有效性和通用性，任意選取各模型參數，對超聲波甘草酸提取過程在相同的條件下做了多組相同的超聲波甘草酸提取實驗。為確保實驗結果的可靠性，每組實驗均重復三次至五次最后求取平均值。通過MATLAB對提取過程構建的三個動力學模型進行實驗仿真[13]，仿真結果如圖7所示。

由圖7中的仿真結果可見，構建的甘草酸提取過程中關于超聲功率、超聲頻率和提取溫度的動力學模型在一定的提取條件下其預測結果跟實測值之間具有較高的擬合度，即本文所建立的超聲波甘草酸提取的三個動力學模型都具有較高的預測精度。為進一步驗證模型精確度，采用平均相對誤差和最大相對誤差作為模型的性能評價指標，分析結果見表4。

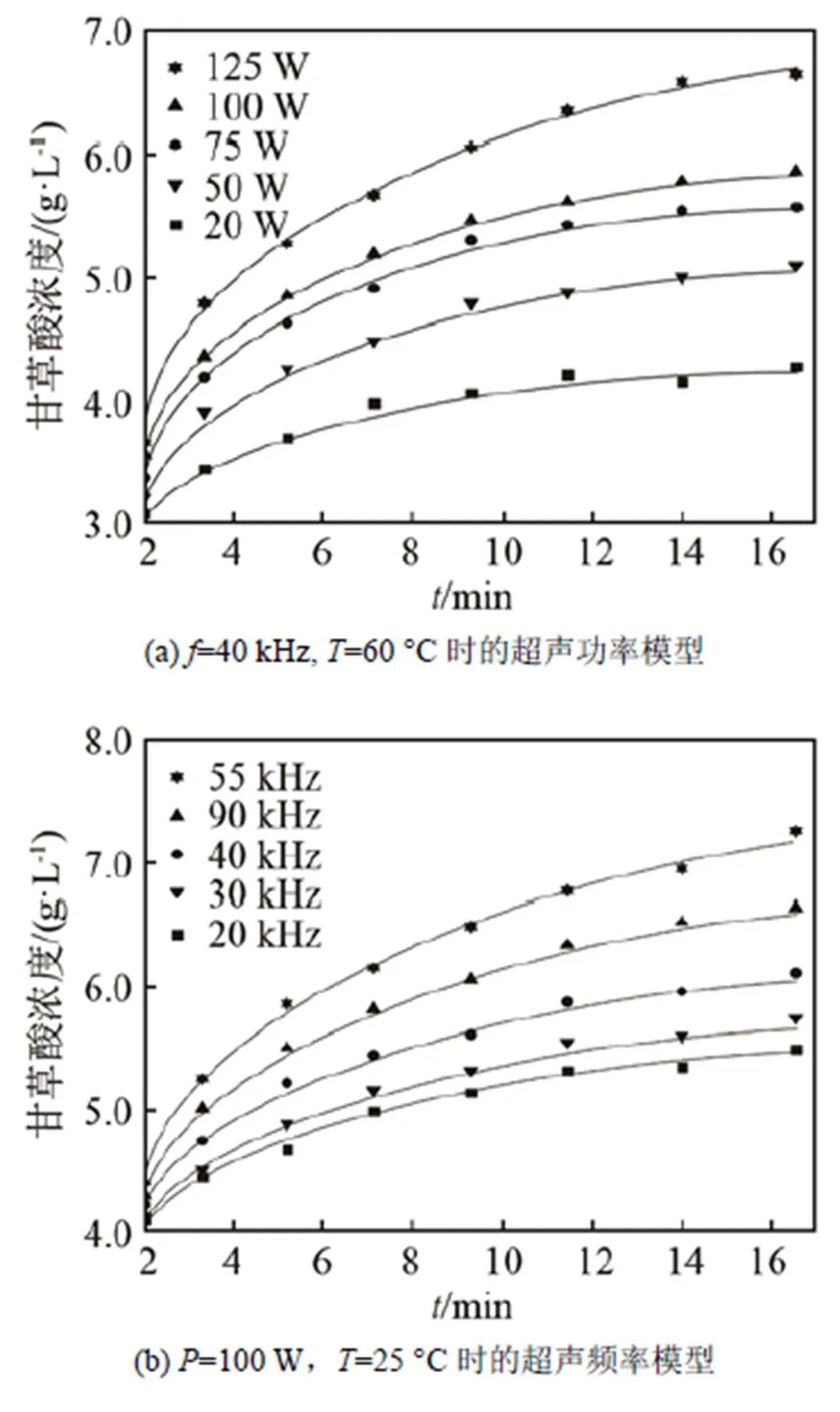
表4 預測值和實驗值之間的相對誤差

從表4中的誤差結果可見，超聲功率動力學模型的最大相對誤差和最大平均相對誤差分別為7.98%和3.66%；超聲頻率動力學模型的最大相對誤差和平均相對誤差的最大值都在9%以下；提取溫度動力學模型的相對誤差的最大值和平均相對誤差的最大值都未超過9%，因此進一步表明本文所構建的甘草酸提取過程的動力學模型具有較高的準確性。

5 結論

(1) 在目前的動力學方程的基礎上，利用超聲波強化機理構建了關于超聲功率、超聲頻率和提取溫度的超聲波提取過程的動力學模型；

(2) 構建了超聲波甘草酸提取過程的動力學方程，包括超聲功率、超聲頻率和提取溫度對提取效果的影響；

(3) 通過數值仿真與實驗對比得到，構建的動力學模型最大相對誤差和最大平均相對誤差分別為8.74%和4.21%。

[1] WILDON A M, BAILEY P J, TASKER P A, et al. Solvent extraction: the coordination chemistry behind extractive metallurgy[J]. Chemical Society Reviews, 2014, 43(1): 123-134.

[2] MUSTAPHA N A H, HII W S, RAHMAN R A, et al. Optimisation of Lipid Extraction from Primary Sludge by Soxhlet Extraction[J]. Chemical Engineering Transactions, 2017, 56: 1321-1326.

[3] SALEH I A, VINATORU M, MASON T J, et al. A possible general mechanism for ultrasound-assisted extraction (UAE) suggested from the results of UAE of chlorogenic acid from Cynara scolymus L.(artichoke) leaves[J]. Ultrasonics Sonochemistry, 2016, 31: 330- 336.

[4] GHAEDI M, GHAZANFARKHANI M D, KHODADOUST S, et al. Acceleration of methylene blue adsorption onto activated carbon prepared from dross licorice by ultrasonic: Equilibrium, kinetic and thermodynamic studies[J]. Journal of Industrial and Engineering Chemistry, 2014, 20(4): 2548-2560.

[5] SUN Y, BI J, ZHANG L, et al. Ultrasound-assisted extraction of three bufadienolides from Chinese medicine ChanSu[J]. Ultrasonics Sonochemistry, 2012, 19(6): 1150-1154.

[6] 盧群, 羅少洪, 丘泰球. 超聲作用下大腸桿菌細胞膜通透性的動力學模型[J]. 聲學技術, 2010, 29 (5): 494-497.

LU Qun , LUO Shaohong, QIU Taiqiu The kinetic model of escherichia coli (E. coli) membrane permeability alteration by ultrasound[J]. Technical Acoustics, 2010, 29 (5): 494-497.

[7] MARIMUTHU E, MURUGESAN V. Influence of ultrasonic condition on phase transfer catalyzed radical polymerization of methyl methacrylate in two phase system-A kinetic study[J]. Ultrasonics Sonochemistry, 2016, 38: 560-569.

[8] 儲茂泉, 劉國杰. 中藥提取過程的動力學[J]. 藥學學報, 2002, 37(7): 59-562.

CHU Maoquan, LIU Guojie. Kinetic model for extraction process of Chinese traditional medicine[J]. Acta Pharmaceutica Sinica, 2002, 37(7): 59-562.

[9] 曹雁平, 矯慶澤. 超聲功率、頻率對姜黃素浸取的影響與動力學模型[J]. 高校化學工程學報, 2011, 25(2): 212-218.

CAO Yanping, JIAO Qingze. Dynamic model of the ultrasound-assisted extraction of the cureumin from curcuma longa land the effects of ultrasound intensity and frequency on the extraction[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(2): 212-218.

[10] LIAO J, QU B, LIU D, et al. New method to enhance the extraction yield of rutin from Sophora japonica using a novel ultrasonic extraction system by determining optimum ultrasonic frequency[J]. Ultrasonics Sonochemistry (1350-4177), 2015, 27: 110-116.

[11] LIAO J, ZHENG N, QU B. An improved ultrasonic-assisted extraction method by optimizing the ultrasonic frequency for enhancing the extraction efficiency of lycopene from tomatoes[J]. Food Analytical Methods (1936-9751), 2016, 9(8): 2288-2298.

[12] 沈慧慧, 艾力·艾山, 王萬強, 等. 響應面優化甘草浸膏中甘草酸超聲提取工藝[J]. 安徽農業科學, 2016, 44(13): 167-170.

SHEN Huihui, Aili·Aishan, WANG Wan-qiang, et al. Optimization of the Ultrasonic Extraction Technique of Glycyrrhizic Acid from Licorice Extract by Response Surface Method[J]. Journal of Anhui Agricultural Science, 2016, 44(13): 167-170.

[13] 廖建慶. 超聲波天然物提取過程建模、頻率優化及應用研究[D]. 無錫: 江南大學, 2017.

LIAO Jianqing. Study on modeling and frequency optimization of ultrasonic extraction process of natural product and its application[D]. Wuxi: Jiangnan University, 2017.

Kinetic model of ultrasonic extraction of glycyrrhizic acid

LIAO Jian-qing1, WANG Han1, WANG Xian-peng2, YUAN Zhi-qiang1

(1. College of Physical Science and Engineering, Yichun University, Yichun 336000, Jiangxi, China; 2. State Key Laboratory of Marine Resources Utilization of the South China Sea, Hainan University, Haikou 570228, Hainan, China)

To provide a theoretical basis for the ultrasonic extraction of glycyrrhizic acid, the existing Chinese herbal medicine leaching kinetics equation is improved based on the ultrasonic enhancement mechanism, and an ultrasonic kinetic model including ultrasonic power, frequency and temperature is proposed. The functional model of Origin7.5 software is used to predict the parameters of kinetic model, namely, the equilibrium concentration of glycyrrhizin and the extraction rate coefficient. A kinetic model was established for predicting the concentration of glycyrrhizic acid as a function of ultrasonic power, frequency, temperature and time. The numerical simulation results show that the maximum relative error of the model prediction is only 8.74%, indicating that the established kinetic model has a good fitting degree. Therefore, it has certain theoretical reference value for the ultrasonic glycyrrhizic acid extraction industry.

ultrasonic; glycyrrhizic acid; kinetic model; extraction

O426；Q62

A

1000-3630(2018)-06-0565-06

10.16300/j.cnki.1000-3630.2018.06.010

2017-11-27;

2018-02-05

江西省教育廳科技項目(GJJ170894, GJJ170915); 國家自然科學基金項目(61701144)

廖建慶(1977－), 男, 江西吉安人, 博士, 講師, 研究方向為超聲波天然物提取過程建模與優化。

廖建慶,E-mail: jndxljqbs@126.com