某柴油機飛輪螺栓設計計算

謝良根

（上海柴油機股份有限公司，上海200438）

0 引言

飛輪螺栓是柴油機主關鍵零件之一，用于連接曲軸與飛輪及離合器，并與連接件一起做高速旋轉運動，不僅需要承載柴油機的靜態輸出載荷，而且需要承載飛輪及離合器的扭振附加載荷。飛輪螺栓的可靠性直接影響柴油機運行安全性。近年來，柴油機的功率不斷提高，后端負載也不斷加大。某柴油機配置一大慣量飛輪，為保障柴油機運行可靠，對飛輪的螺栓設計計算進行研究，以期提高飛輪螺栓設計的安全可靠性。

1 螺栓預緊力計算方法

目前，柴油機裝配流水上飛輪螺栓擰緊工藝一般采用扭矩法和扭矩+轉角法2種方法。由于這2種螺栓擰緊方法的工藝側重點不同，其對應的螺栓預緊力計算公式也不同。

1.1 扭矩法螺栓預緊力計算

扭矩法是通過控制擰緊螺栓時的擰緊力矩值來達到控制螺栓預緊力大小的螺栓擰緊工藝。分析扭矩法擰緊狀態下的螺栓受力情況可知，扭緊力矩Tt等于克服螺紋之間相對轉動的阻力矩T1和螺栓支撐面上的摩擦阻力矩T2之和，計算如下[1]：

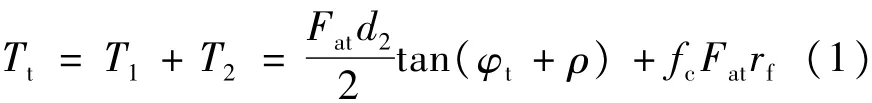
式中，Fat為軸向預緊力，N；d2為螺紋中徑，mm；φt為螺紋升角， （°）；ρ為摩擦角， （°）；fc為螺栓法蘭面與被連接件支承面之間的摩擦系數；rf為支承面摩擦半徑，mm。

1.2 扭矩+轉角法螺栓預緊力計算

扭矩+轉角法是在扭矩法的基礎上，通過直接控制螺栓伸長量來達到控制螺栓預緊力大小的螺栓擰緊工藝，螺栓伸長量是通過控制螺栓擰緊角度來實現。轉角法螺栓預緊力Faa的計算如下[2]：

式中，θ為扭緊角度，（°）；P為螺距，mm；δS為螺栓柔度，mm/N；δP為被連接件柔度，mm/N。

計算扭矩+轉角法螺栓擰緊力時需要采用公式（1） 和公式 （2）。

2 飛輪螺栓受力分析

2.1 發動機基本參數

待設計計算的飛輪螺栓用于某柴油機，其基本參數表1。

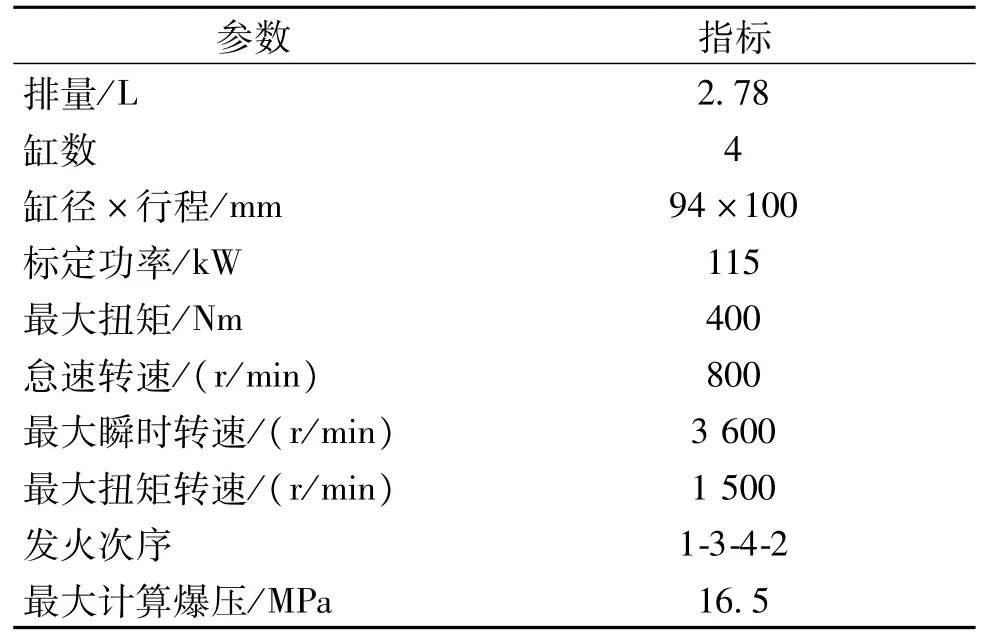
表1 某柴油機基本參數

2.2 飛輪動態扭矩分析

借助多體動力學軟件AVL EXCITE designer完成飛輪螺栓承載的動態扭矩計算。為了獲取飛輪螺栓承載的最大動態扭矩，計算時輸入柴油機在外特性工況下且按照飛輪端100%功率輸出時的示功圖，如圖1所示。在不同減振器頻率下的飛輪螺栓承載的動態扭矩仿真計算結果如圖2所示。根據計算結果可知，在2 800 r/min時，飛輪螺栓承載的最大動態扭矩T為2 947.89 Nm。

2.3 飛輪螺栓所需要的最小預緊力分析

飛輪和曲軸的裝配關系如圖3所示，有效摩擦面外徑為108 mm，有效摩擦面內徑為60.3 mm。有效摩擦面半徑reff計算公式如下[3]：

式中，D為有效摩擦面外徑，mm；d為有效摩擦面內徑，mm。

圖1 外特性工況示功圖

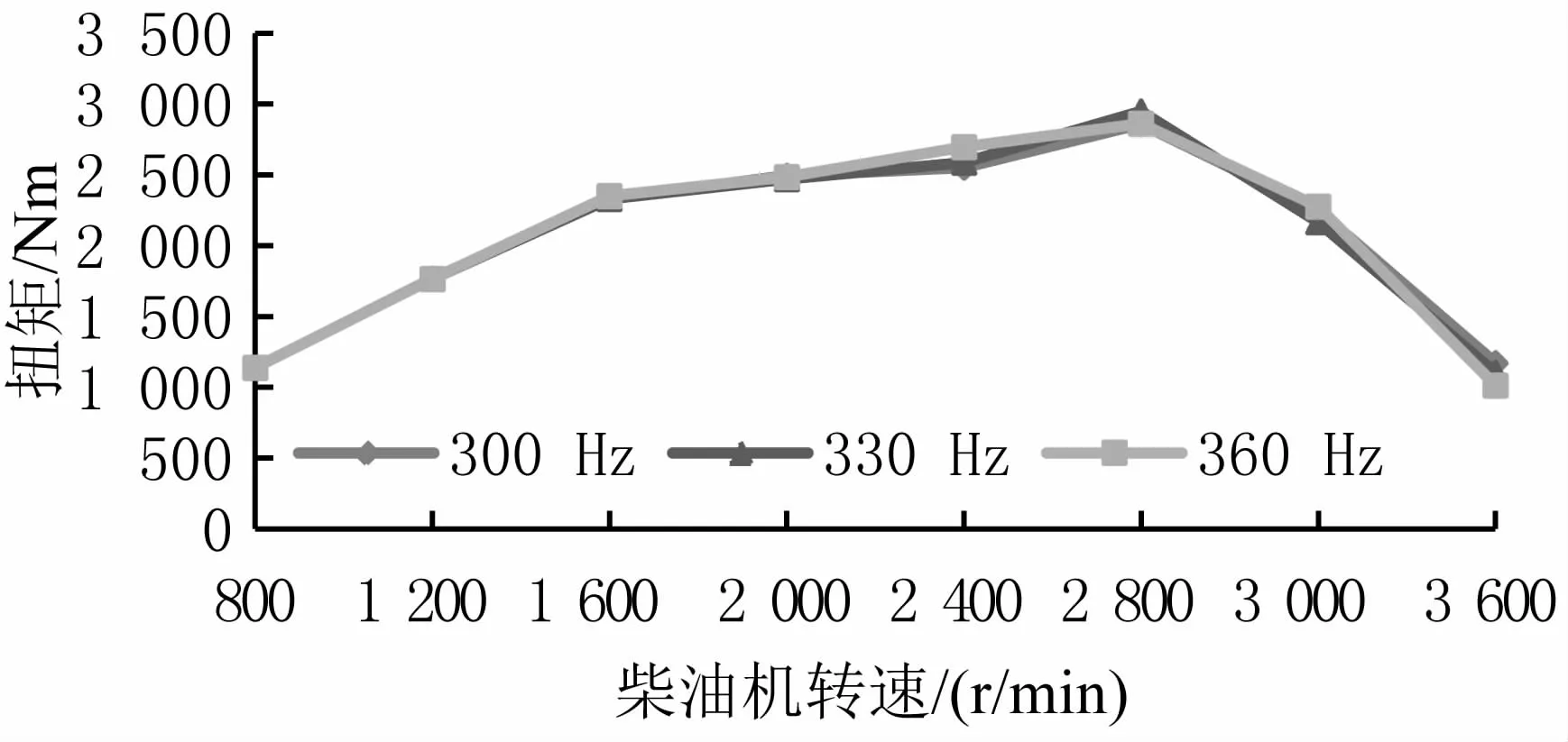
圖2 飛輪螺栓動態扭矩

圖3 飛輪與曲軸裝配關系

通過計算，有效摩擦面半徑 reff為43.2 mm；根據經驗數據庫，設定摩擦系數μ為0.15，設定飛輪螺栓覆蓋系數S≥1.1；根據前面分析，飛輪螺栓承載的最大動態扭矩T為2 947.89 Nm。

如果在摩擦面內圓周均布n個螺栓，則飛輪螺栓需要的最小預緊力Fmin，計算公式如下：

根據計算，如果布置8個飛輪螺栓，所需要的最小螺栓預緊力62.55 kN；如果布置10個飛輪螺栓，所需要的最小螺栓預緊力50.04 kN。

3 飛輪螺栓設計計算

3.1 飛輪螺栓方案

根據柴油機后端空間布置及對飛輪螺栓對標分析，擬定2種螺栓方案：10個規格為M10×1.25，機械性能為12.9級的螺栓 （10-M10×1.25-12.9，方案1）；8個規格為M12×1.25，機械性能等級為12.9的螺栓 （8-M12×1.25-12.9，方案2），并分別進行理論校核計算。

3.2 方案1螺栓預緊力計算

根據發動機技術要求，制定螺栓擰緊工藝，確定采用扭矩+轉角法。第1步施加扭矩 （30±5）Nm；第2步施加轉角50°±3°。由于采用扭矩+轉角法擰緊工藝，根據前面分析，需要計算螺栓和被連接件的剛度。

3.2.1 螺栓剛度計算

根據德國標準VDI2230-2003螺栓緊固標準[4]定義，建立螺栓剛度計算模型，如圖4所示。其中lSK為螺栓頭部等效變形長度，lk為被連接件長度，l1為螺栓光桿部長度，l2為螺栓縮頸長度，lGew為未嚙合螺紋長度，lGM為等效嚙合螺紋變形長度。

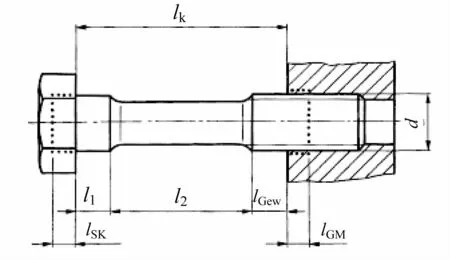
圖4 螺栓剛度計算模型

根據計算模型計算螺栓的柔度，首先計算螺栓軸向各段柔度δi，計算公式如下：

式中，δi為螺栓軸向 i段柔度，mm/N，li為螺栓軸向i段長度，mm；ES為螺栓楊氏模量，即彈性模量，MPa；Ai為螺栓i段有效截面積，mm2；li為 lSK、 l1、 l2、 lGew和 lGM。

然后將計算得到的各段柔度求和，得螺栓總柔度 δS：

式中，δSK為螺栓頭部等效變形段柔度，mm/N；δ1為螺栓光桿段柔度，mm/N；δ2螺栓縮頸段柔度，mm/N；δGew為未嚙合螺紋段柔度，mm/N；δGM為等效嚙合螺紋變形段柔度，mm/N。

通過計算，螺栓的總柔度為1.93E-06 mm/N，螺栓的剛度為5.18E+05 N/mm。

為了提高螺栓剛度計算效率，本計算嘗試采用有限元軟件計算螺栓剛度。利用Abaqus軟件，對飛輪螺栓按照圖4所示的模型結構進行建模并計算。設定螺栓的材料屬性，并采用C3D10M修正的二次四面體單元網格，約束螺栓法蘭面，并在螺栓底部施加50 kN的拉力。計算結果如圖5所示，螺栓的底面最大變形量0.092 73 mm。由此可以算出飛輪螺栓的剛度為5.39E+05 N/mm。與直接由公式 （5）和公式 （6）計算得的剛度5.18E+05 N/mm比較，誤差在5%以內，證明了有限元法的正確性和可行性。

圖5 螺栓變形量

3.2.2 被連接件剛度計算

根據德標VDI2230-2003螺栓緊固標準定義，被連接件的螺栓軸向壓應力隨著距離螺栓頭部法蘭環形壓面增大而減小，所以將被連接件等效為圓錐體計算其剛度。被連接件剛度計算模型如圖6所示，其中dw為螺栓頭部法蘭承壓面直徑，h為被連接件等效變形圓錐體高度，dh為螺栓孔直徑，φ為等效變形圓錐體圓錐角，Dk為等效變形圓錐體最大外徑，DA為結合面處的等效外徑，D′A為被連接件實體的等效外徑。

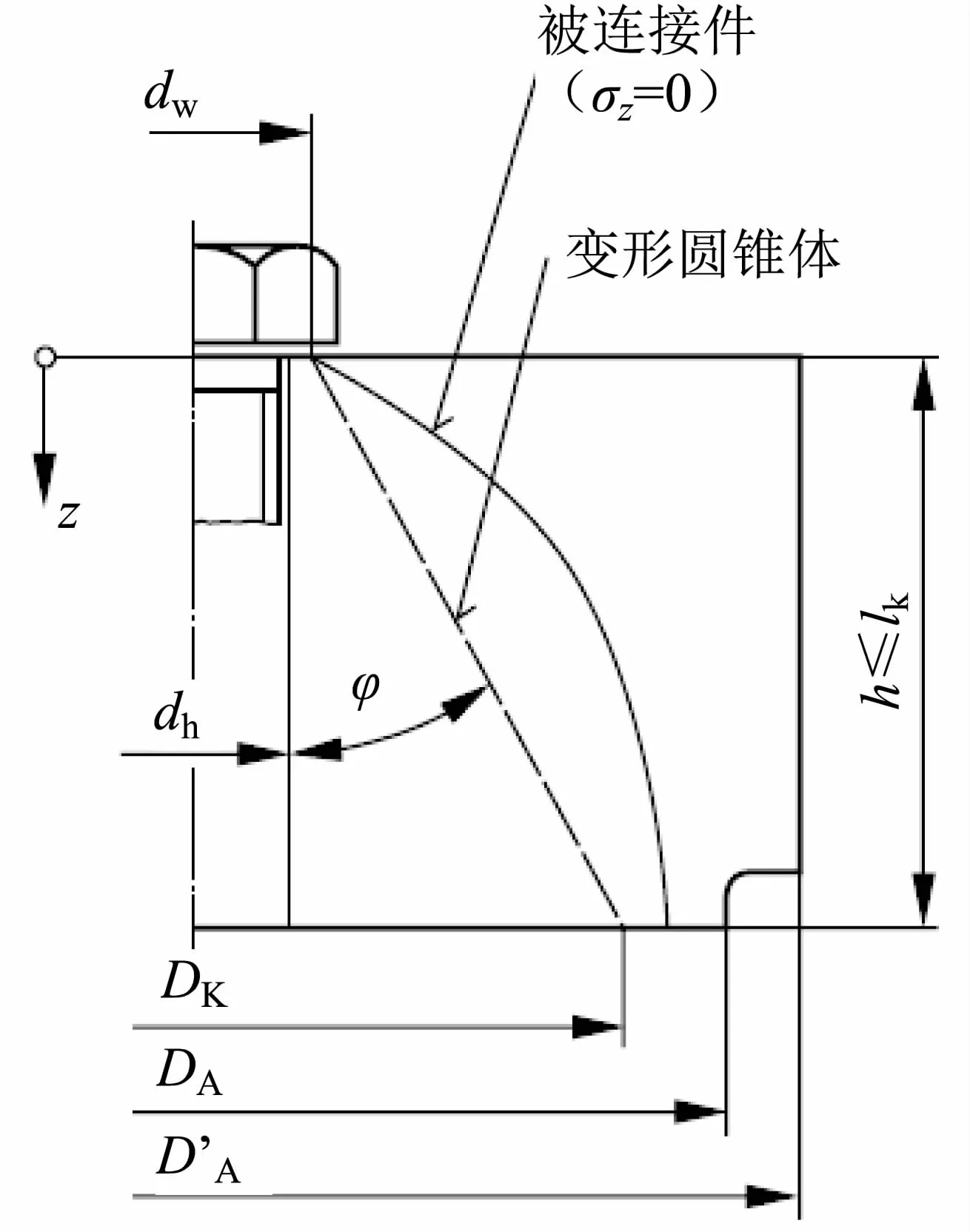
圖6 被連接件剛度計算模型

對圖6所示的各段被連接件柔度進行積分，計算出被連接件的總柔度δP，計算公式如下：

式中，d z為被連接件軸向z微段長度，mm；E（z）為被連接件軸向 z微段楊氏模量，MPa；A（z）為被連接件軸向z微段截面積，mm2。

根據計算，被連接件總柔度 δP為5.36E-07 mm/N，所以被連接件的剛度為1.87E+06 N/mm。

為了提高被連接件剛度計算效率，本計算同樣嘗試采用有限元軟件計算被連接件剛度。利用Abaqus軟件，對被連接件飛輪和螺栓墊圈進行分析。設定飛輪和螺栓墊圈的材料屬性，并采用C3D10M修正的二次四面體單元網格。飛輪和螺栓墊圈采用TIE的方式綁定，約束飛輪和曲軸安裝面的6個自由度，并在每個螺栓墊圈與螺栓的接觸面處施加軸向50 kN的壓力。計算結果如圖7所示，被連接件最大變形量0.027 94 mm。由此可以得到飛輪螺栓的剛度為1.79E+06 N/mm。與直接由公式 （7）計算得的被連接件剛度1.87E+06 N/mm比較，誤差在5%以內，證明了有限元法的正確性和可行性。

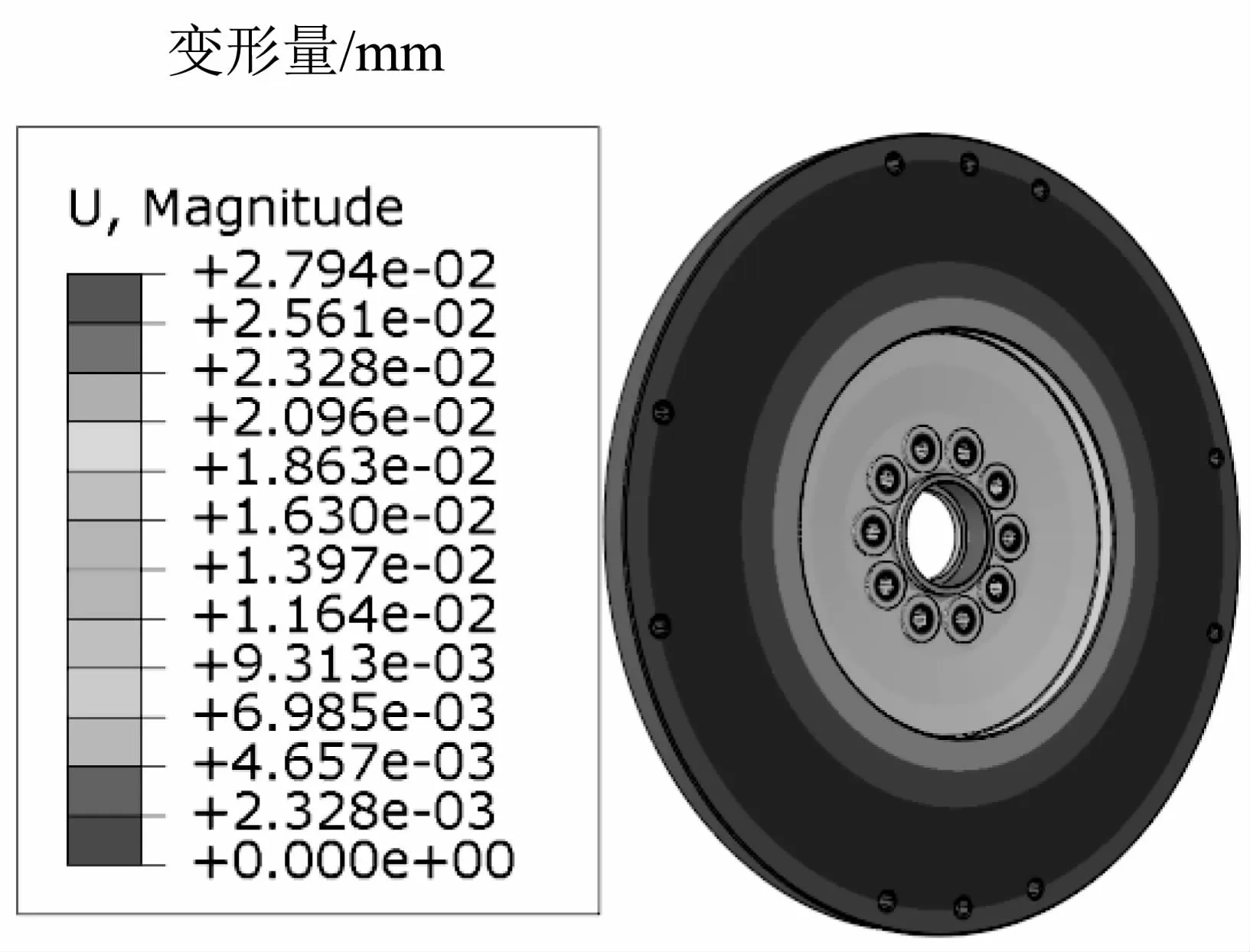
圖7 被連接件變形量

3.2.3 螺栓預緊力計算

根據對標數據庫，設定螺栓頭部法蘭面和螺紋處的摩擦系數均為0.3±0.02。利用基于 “第四強度理論”[5]和德國標準VDI2230-2003螺栓標準編制的螺栓預緊力計算軟件，進行飛輪螺栓預緊力計算。按照預先制定的扭矩+轉角法擰緊工藝，即第1步施加扭矩 （30±5）Nm，第2步施加轉角50°±3°， 擰緊 10個飛輪螺栓 （M10×1.25-12.9）。螺栓預緊力計算結果如表2和圖8所示。飛輪螺栓的預緊力為44.51～55.73 kN，不滿足必須大于所需最小值50.04 kN的要求，故此方案不可行。

3.3 方案2螺栓預緊力計算

根據發動機技術要求，制定擰緊工藝，確定采用扭矩+轉角法扭緊：第1步施加扭矩 （30±5）Nm；第2步施加轉角60°±3°。采用此擰緊工藝，計算螺栓預緊力同樣需要先計算螺栓和被連接件的剛度。

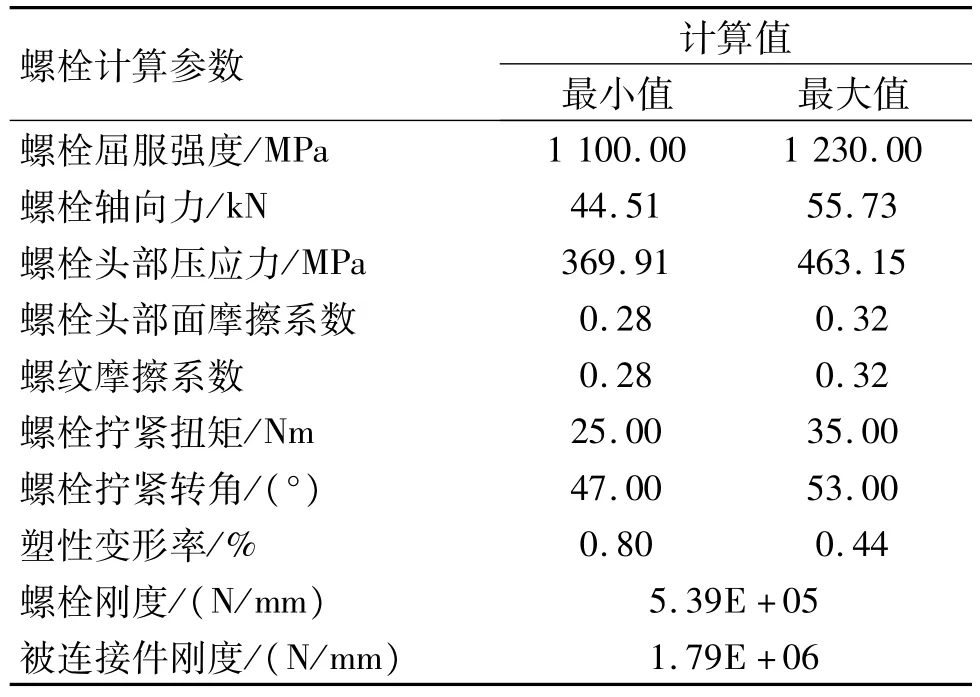
表2 飛輪螺栓預緊力計算結果

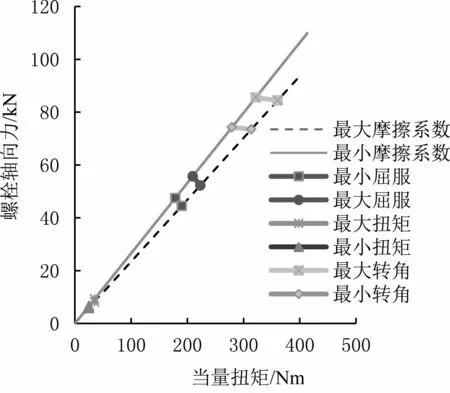
圖8 飛輪螺栓預緊力計算結果

3.3.1 螺栓剛度計算

根據以上分析，公式法和有限元法都可滿足螺栓剛度計算精度。為了提高螺栓剛度計算效率，直接采用有限元法進行剛度計算。利用Abaqus軟件，如前所述完成前處理工作，并在螺栓底部施加50 kN的拉力。計算結果如圖9所示，螺栓底面最大變形量0.067 74 mm，由此可以算出飛輪螺栓的剛度為7.38E+05 N/mm。

3.3.2 被連接件剛度計算

同樣，直接用有限元法對被連接件的剛度進行計算。利用Abaqus軟件，如前所述完成被連接件飛輪和螺栓墊圈的前處理工作，飛輪和螺栓墊圈采用TIE的方式綁定，約束飛輪和曲軸安裝面的6個自由度，并在每個螺栓墊圈與螺栓的接觸面處施加50 kN的軸向壓力。計算結果如圖10所示，被連接件最大變形量0.025 38 mm，由此可以得到被連接件的剛度為1.97E+06 N/mm。

圖9 螺栓變形量

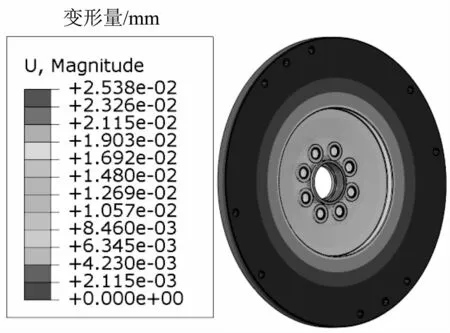
圖10 被連接件變形量

3.3.3 螺栓預緊力計算

根據對標數據庫，設定螺栓頭部法蘭面和螺紋處的摩擦系數均為0.3±0.02。仍然利用基于 “第四強度理論”和德國標準VDI2230-2003螺栓標準編制的螺栓預緊力計算軟件，進行飛輪螺栓預緊力計算。按照預先制定的扭矩+轉角法扭緊工藝，即第1步施加扭矩 （30±5）Nm，第2步施加轉角60°±3°， 擰緊8個螺栓 （M12×1.25-12.9）。 螺栓預緊力計算結果如表3和圖11所示。飛輪螺栓的預緊力為68.06～85.15 kN，滿足大于所需最小值62.55 kN的要求，故此方案可行。

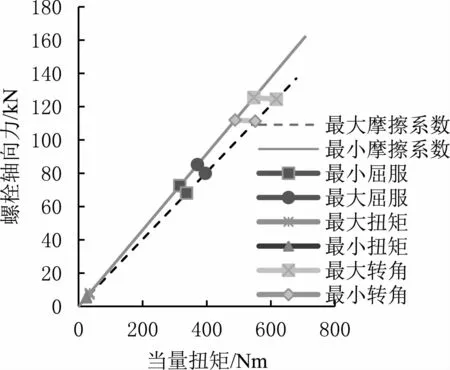
圖11 飛輪螺栓預緊力計算結果

4 飛輪螺栓預緊力試驗驗證

根據上述計算分析結果，確定方案2，即8-M12×1.25-12.9，并完成螺栓樣件試制。由于計算螺栓預緊力時，螺栓的屈服強度和摩擦系數的輸入數值均從自建的對標數據庫選取，所以必須通過螺栓預緊力超聲試驗進行確認。螺栓預緊力超聲試驗如圖12所示。螺栓預緊力超聲試驗方法如下：首先，按預先制定的扭矩+轉角法扭緊工藝擰緊，第1步施加扭矩 （30±5）Nm，第2步施加轉角60°±3°，擰緊8個飛輪螺栓；然后，采用螺栓預緊力超聲波測量儀測量飛輪螺栓應變；最后，通過預先標定的飛輪螺栓應力應變關系，計算飛輪螺栓的預緊力。飛輪螺栓預緊力試驗結果如表4所示。飛輪螺栓預緊力測試結果為68～83 kN，滿足大于最小值62.55 kN的要求；同時，與理論計算值68.06～85.15 kN基本一致，證明了螺栓設計計算的合理性。

圖12 飛輪螺栓預緊力超聲試驗

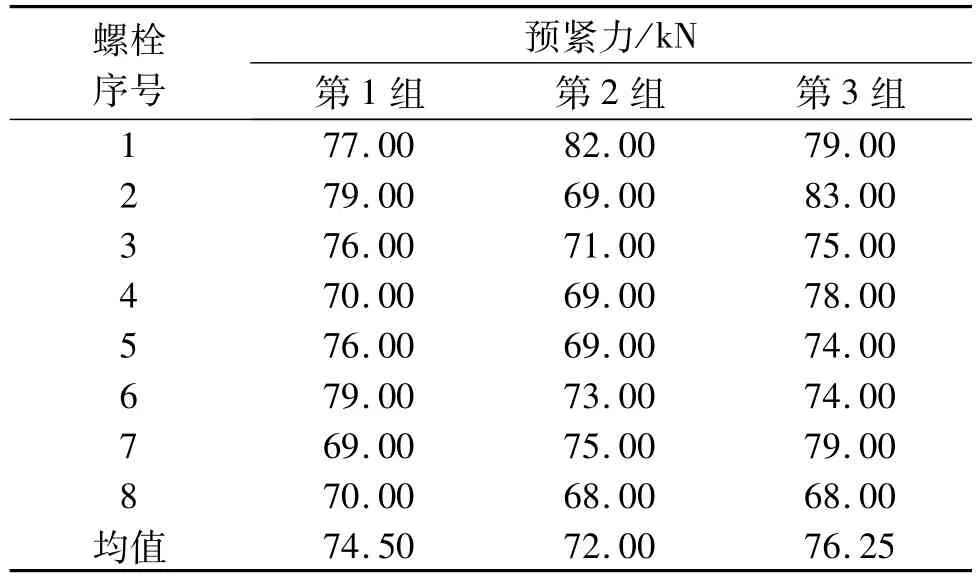
表4 飛輪螺栓預緊力超聲試驗結果

5 結論

（1）柴油機飛輪螺栓不僅需要承載柴油機后端靜態輸出扭矩，而且需要承載飛輪及離合器的動態扭振附加扭矩。根據以往經驗，柴油機飛輪及離合器的動態扭振附加扭矩一般是靜態輸出扭矩的3倍以上，所以設計飛輪螺栓時，需要重點關注柴油機飛輪及離合器的扭振附加扭矩。由于柴油機后端配套的多樣性，不同飛輪和離合器的配置都會導致飛輪螺栓承載力的變化，所以飛輪螺栓設計之初，需要經過大量的計算，以便獲取螺栓所需要的最小預緊力。

（2）飛輪螺栓是柴油機主要關鍵零件之一，為了保證其預緊力一致性及可靠性，往往采用扭矩+轉角法擰緊工藝。計算采用此擰緊工藝的螺栓預緊力時，需要準確地計算飛輪螺栓和被連接的剛度。采用有限元法計算零件剛度可提高計算效率，與用公式法計算結果對比分析，證明有限元法是正確的、可行的，這為飛輪螺栓設計計算提供了高效且有效的參考和依據。

（3）由于飛輪螺栓預緊力計算時，螺栓的屈服強度和摩擦系數因受多種因素影響而存在不確定性，往往采用經驗值，所以在飛輪螺栓設計計算完成后，必須進行螺栓樣件預緊力超聲試驗，以確定螺栓設計計算的合理性。