基于改進的NSGA-II的多目標魯棒性設備布局研究*

張萍萍，鄭飂默，王詩宇

(1.中國科學院大學，北京 100039；2.中國科學院沈陽計算技術研究所 高檔數控國家工程研究中心， 沈陽 110168；3.沈陽高精數控技術有限公司，沈陽 110168)

0 引言

企業在構建制造系統初期階段，設備布局是首要解決的問題之一。研究表明，合理的設備布局至少可以節約10%～30%的物料運輸費用[1]。在動態多變的市場環境下，靜態布局(SFL)[2-3]方法已經無法滿足生產需求。如果采用中斷生產重新進行設備布局來滿足生產需求，會對企業造成較大的損失。如何使布局在動態多變的需求下，表現出良好的柔性和魯棒性，是企業能否持續發展的關鍵之一。

用戶需求的動態性,導致傳統的靜態布局無法滿足在連續的生產過程中后期的生產計劃；同時又因為制造系統的復雜性，不可能在設備布局無法滿足生產計劃時，調整設備位置或重新布局。因此在制造系統設計初期提供一種布局方案，這種布局方案在動態的需求下，也能很好的滿足生產任務，“不變應萬變”，即魯棒性設備布局。

1987年，Meir Rosenblatt等[4]首次將魯棒性概念引入到制造業設備布局領域，使設備布局對動態的生產任務表現出良好的性能。魯棒性布局是指存在一種布局方案能滿足各階段不同的生產需求，對于其中某個特定階段，它不一定是最優方案，但對整個生產周期卻是最優的布局方案。Ghorbanali Moslemipour等[5]針對魯棒性布局問題進行了綜述，詳細總結了以往文獻中所采用的優化模型及求解算法。劉瓊等[6]則針對設施面積不等的作業車間作為研究對象，以最小化物流搬運費用和面積費用為優化目標，建立魯棒性布局模型，并提出一種改進的蛙跳算法對其進行求解。李愛平等[7]考慮到物流搬運系統的設計對魯棒性布局的影響，提出設備魯棒性布局方案及物料搬運系統協同優化方法。目前魯棒性布局的研究中采用的優化算法大都是采用加權系數將多目標單一化，但是由于加權系數的值對結果的影響較大，因此采用基于Pareto最優前沿的方法在多目標空間內直接求解，不再需要將多個目標進行單一化處理。在基于Pareto尋優的多目標優化算法[8]中，DEB在2002年提出的帶精英策略的非支配排序遺傳算法(Non-dominated Genetic Algorithm II,NSGA-II)是一種有效的算法，已被國內外廣泛用來求解多目標優化問題。

根據上述研究現狀，針對魯棒性設備布局問題的多目標多約束的特點，以物料搬運費用、非物流關系和面積費用為優化目標建立布局模型，并利用改過的NSGA-II算法對其求得Pareto解集，用戶根據實際情況擇優選取布局方案。最后，通過實例驗證模型和算法的有效性。

1 數學模型

1.1 問題描述

魯棒性布局問題是連續P個生產計劃期最穩定的布局方案。根據產品的工藝路線和各個子計劃期設備間的物流矩陣等約束條件的變化，分析整個生產周期，引入魯棒性指標，最后合理確定車間設備的具體位置。

以已知的n臺設備為研究對象，以最小化車間物料搬運費用、非物流關系和面積費用為優化目標，建立多目標魯棒性布局模型。

假設條件：①設備均為矩形結構，且長寬已知；② P個階段的生產計劃已定；③各產品的工藝路線已定；④同行設備的中心點位于同一條水平線上；⑤設備間的物料搬運只能走水平和垂直直線。

1.2 優化目標

以物流費用，非物流關系及面積費用作為優化目標，具體分析如下：

(1) 物流搬運費用最小化。其中：i和j表示車間設備，i,j[1,2,…,n];xi和yi為設備i的坐標值；Cij表示多設備i到設備j的單位距離物料搬運費用；fpij表示p階段從設備i到設備j的物料搬運量。由文獻[5]對魯棒性布局問題的總結，建立車間物料搬運費用的計算公式，如式(1)，其中Dij表示設備i與設備j的距離。

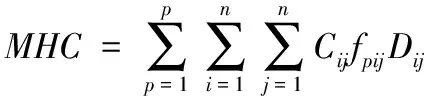
(1)

(2) 非物流關系最大化。根據 LEEK等人的研究，非物流關系可表達為：

(2)

cij為設備之間的非物流密切度值，如表 1 所示，bij是布局方案中設備之間的密切度關聯因子，它由資源間的實際物流距離dij和最大可能距離dmax決定，如表2所示。

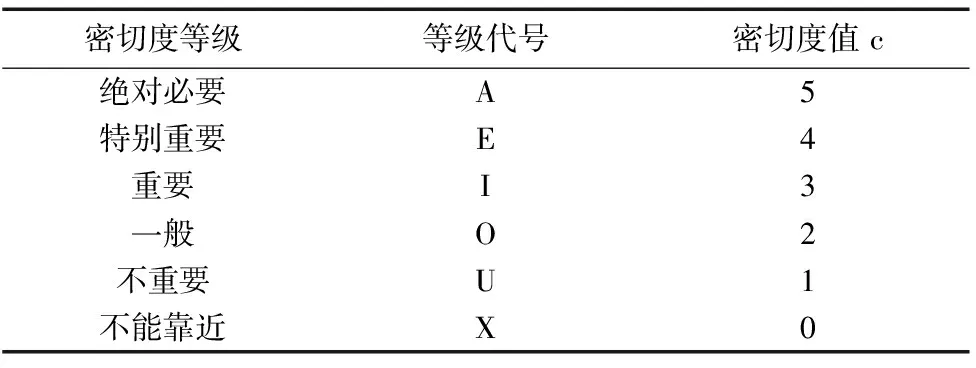
表1 設備關系密切度分類

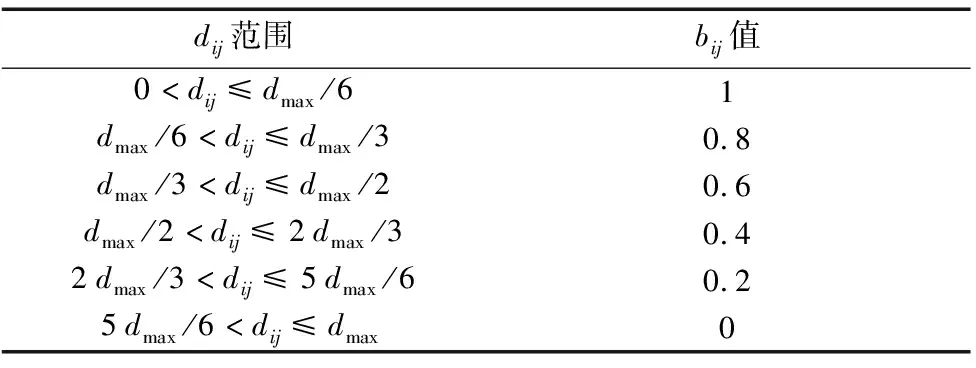
表2 密切度關聯因子

非物流關系的值越大，表明非物流關系越密切，為方便利用 NSGA- II 編程解決多目標布局問題，非物流關系目標函數如式(3)所示。其中M為一個較大的常數，可根據實際情況選擇。

(3)

(3) 車間面積費用最小化。采用設備自動換行的布局策略，即在同一行內的各設備長度及其設備相互間距之和超過了布局車間的長度，則該行最后一臺設備自動進入下一行。

設備占地總面積簡化為矩形，長度為車間總長度L，寬度為h，h可以表達為：

h=(m-1)×s+s0+0.5×wi-(s0-0.5×wj)

其中，wi為最后一行上的設備的最大寬度，wj為第一行上的設備的最大寬度，s為行間距，s0為第一行設備與車間上邊界之間的最小距離，m為布局行數。不同布局方式中處于邊界的設備不同，h的取值也會相應地發生變化；R為單位土地面積費用。

因此，面積費用公式如式(4)所示：

AC=min{R·L·h}

(4)

1.3 約束條件

(1) 邊界約束和空間約束：式(5)保證車間設備不重疊，由于使用自動換行策略，Y方向上的行間距根據設備尺寸設定，設備之間不會出現重疊放置；式(6)保證一臺設備只能被放置一次，式(7)保證在設備自動換行的布局策略下，設備不超過車間寬度；

(i,j=1,2...,n,i≠j)

(5)

(6)

h≤H

(7)

Xi和Yi表示設備i的長和寬；sij表示設備i與j的X向最小間距；L和H為車間的長和寬；hi0為設備i離車間邊距界的X向和Y向最小間距；zik是0～1決策變量，其中zik=1，表示設備i在k行上，zik=0，表示設備i不在k行上，k為設備所有的行。

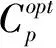
Rc≤δ

(8)

(9)

2 優化算法設計

為了對上述模型進行化化計算，在NSGA-II的基礎上引入了DE策略[9-10]，從而使獲得的Pareto最優解集保持較好的多樣性，加快算法的收斂速度。

2.1 染色體編碼/解碼機制

染色體編碼采用實數編碼方式，每個染色體由兩部分組成表示一種布局方案，這兩部分分別為設備排列順序和設備間凈間距。

[{Mv,Mr,…,Mu,…,Mz},{Δ1,Δ2,…,Δi,…,Δn}]

其中，Δ1表示設備Mv與車間邊界的最小距離，Δi表示第i臺設備與第i-1臺設備之間的凈間距，取值范圍為[Umin,Umax]。由于采用自動換行的布局策略，當第i臺設備剛好是某一行的第一臺設備時，Δi表示第i臺設備與車間邊界的最小距離。

染色體的解碼即求解每臺設備中心對應的坐標值，設備坐標的求解公式為：

yk=(t-1)×s+s0

(10)

(i,k=1,2,…,n;t=1,2,…m)

其中，n為設備的數量，t為該染色體對應的布局行數。

2.2 遺傳算子

(1) 二元錦標賽選擇算子

通過快速非支配排序以及擁擠度計算之后，種群中的每個個體都得到兩個屬性：非支配序rank和擁擠度nd。利用這兩個屬性，可以區分種群中任意兩個個體的支配和非支配關系。個體優劣比較依據為：當且僅當irankjd，個體i優于個體j。

選用二元錦標賽選擇算子，從種群中隨機選擇兩個個體，根據非支配排序和擁擠度比較兩個個體，選擇最優的個體進入交配池。

(2) 交叉算子

對于染色體的設備排列序列部分采用映射交叉(PMX)算子。

(3) 基于差分進化的進化算子

對于設備凈間距序列部分，引入DE策略進行交叉和變異，提高算法局部搜索能力，在進行精英保留策略選擇子代個體時擁有較高的競爭能力，即在一定程度上保證了個體的多樣性。

在DE中，常見的差分策略是隨機選取兩種群中兩個不同的個體，將其向量差縮放后與待變異個體進行向量合成，即：

Ti=Xr1+F×[Xr2-Xr3]

其中，T為變異目標個體；F為縮放因子；Xr1表示種群中第r1個個體。F[0,1]；r1≠r2≠r3≠i。在進行變異操作時，為了保證解的有效性，要保證各“基因”滿足邊界條件，如果不滿足邊界條件，則隨機重新生成。

對xi及其變異的中間體Ti進行個體間的交叉操作：

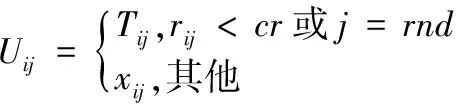
其中，Tij為變異個體Ti的第j個變量，j[1,NP]；rij為個體i第j個變量對應的均勻分布的一人隨機變理，rij[0,1]；rnd為均勻分布的整數，rnd[1,NP]；cr為交叉概率，cr[0, 1]。

2.3 懲罰項

由于采用自動換行的布局策略，因此設備在X方向上不會超出工作區域。所以只需要判斷在Y方向上最后一行的設備是否會超出車間區域。Pt為Y方向超出車間區域的懲罰項，如式(11)，其中m為布局行數，w最后一行設備的最大寬度，T為正的大數懲罰項。

(11)

2.4 算法流程

采用改進后的NSGA-II算法求解已建立的優化模型，DE-NSGA-II算法過程如圖1所示。首先將第t代產生的新種群Qt與父代Pt合并組成Rt，種群大小為2N，然后對Rt進行非支配排序，產生一系列非支配集Zi并計算擁擠度。由于子代和父代個體都包含在Rt中，則經過非支配排序以后的非支配集Z1中包含的個體是Rt中最好的，所以先將Z1放放新的父代種群Pt+1中，依次類推，直到添加Zi時，種群的大小超出N，此時對Zi中的個體使用擁擠度比較，取前(N-num(Pt+1))個元素添加到新的父代種群Pt+1中。對新的父代種群進行選擇、交叉、變異操作，產生新的子代種群。

如此反復迭代直至達到最大迭代次數，得到pareto最優解集。為了使得到的布局方案滿足魯棒性的要求，需要驗證pareto解集中是否存在滿足魯棒性約束的解，若存在這樣的解，則對該解進行解碼，即得到魯棒性布局方案，最后算法可能得到不只一種滿足魯棒性的布局方案，如果沒有一個解滿足魯棒性要求，則重啟算法。

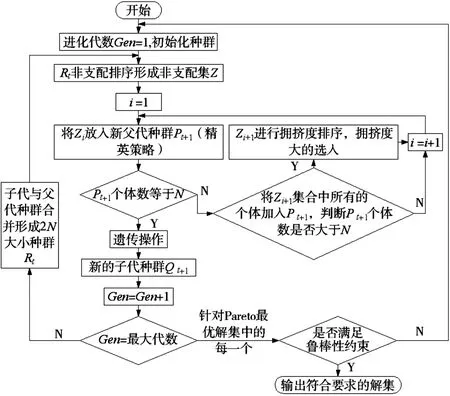
圖1 NSGA-II算法流程

3 實例研究

3.1 實例描述

應用上述算法對某柔性制造單元的布局問題進行求解。該柔性制造單元的長為12m，寬為10m，需對12臺設備進行布局設計，設備的具體尺寸如表3所示。設備間的凈間距?的取值范圍為[0, 1.5]，設備間行間距s為2m，第一行設備與車間邊界距離s0為1.2m。設懲罰值T=500元，土地面積費用R=500元/m2。分析整個生產周期的實際情況以及車間安全性，可得到非物流關系cij，設備間水平最小間距要求hij和設備與車間邊界的最小距離要求hi0；魯棒性指標δ=0.07。

分析該制造單元連續3個計劃期的工藝路線(表4)和物流信息(表5)，求解每個階段的物流搬運頻率矩陣。

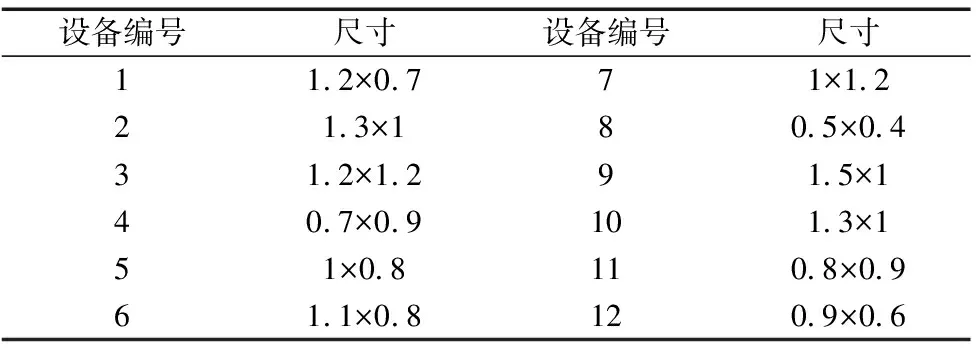
表3 設備尺寸(m×m)

表4 工藝路線

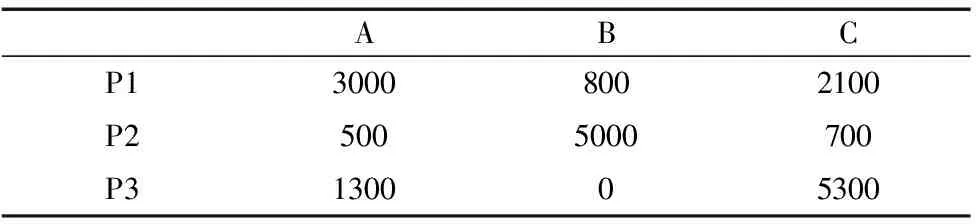
表5 生產計劃

3.2 算法參數設計與問題求解

DE-NSGA-II算法的相關參數設置如下：種群規模pop=100；最大遺傳代數maxgen=100；交叉概率pc=0.7，以式(1)～式(3)為目標函數，運行程序，最終得到的Pareto解集如圖2所示。針對提出的魯棒性布局模型分別應用DE-NSGA-II、NSGA-II，SADE對該魯棒性布局模型進行多次求解，結果對比，與NSGA-II及SADE相比，DE-NSGA-II的收斂性和多樣性更好，對比結果見表6。

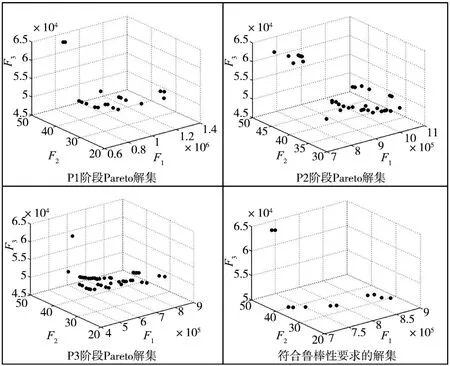
圖2 pareto解集

在最終的Pareto解集中，剔除相似度比較高的布局方案，得到如表7所示的5種布局方案。方案1的目標1值是所有解集中最小的，但是目標2和目標3的值是最大的；方案5的目標3的值是最小的，但是目標1的值是最大的；方案4的目標2的值是所有解集中最小的，但是目標1和目標3的值均不是最小的。通過多次實驗分析可得，不存在某種方案可以使得3個目標都達到最優。

該實例三個目標的最優解分別為F1=729698.92，F2=33.8，F3=50040，不存在任何一個個體能使三個目標值同時達到最優。企業決策者可以根據實際情況，在多種方案中選擇最合適的布局方案。

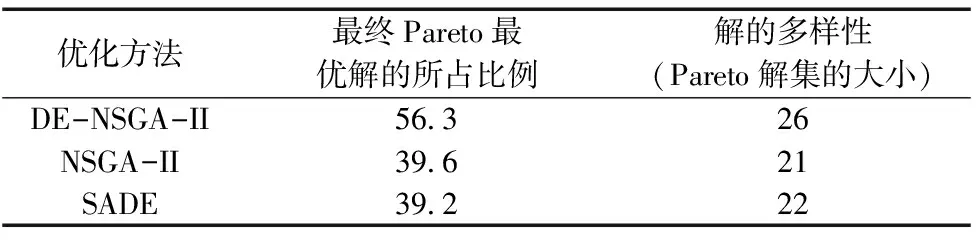
表6 三種優化算法性能對比

表7 部分Pareto解集

4 結束語

針對提出的魯棒性布局模型，利用基于差分進化與NSGA-II的多目標算法驗證了該模型的有效性，克服了使用加權系數將多目標單一化求解多目標問題的缺點，可以有效地應對復雜多變的市場需求。算法設計的過程中，在NSGA-II算法的基礎上引入DE策略，有效地提高了Pareto解集的多樣性和算法的收斂速度，最終得出符合魯棒性要求的布局方案集。