基于非奇異終端滑模的制動缸自抗擾控制研究*

劉芳璇, 謝程程, 彭 慧, 王桂榮

(1.西安鐵路職業技術學院 ,西安 710026;2.喀什師范學院 物理系, 新疆 喀什 844000;3.中國計量大學 機電工程學院，杭州 310018)

0 引言

現代電力機車基礎制動裝置通常采用獨立的踏面制動單元,通過閘瓦與輪對踏面的直接接觸(能耗制動)產生制動力迫使機車制動,并將其動能熱散逸[1]。因此,應對閘瓦位置控制動態響應和精度進行合理設計,防止其響應緩慢或與踏面過分接觸,從而避免制動不及時或抱死滑行現象,確保閘瓦的制動可靠性和使用壽命[2]。

實際工況中,閘瓦通過連桿機構與制動缸活塞一側相連,活塞另一側連通高壓風源,其壓力值取決于控制其流速大小的伺服閥閥芯開度,而閥芯開度由控制電壓所決定,因此需通過對電壓的控制保證輪瓦接觸間隙在許用范圍之內。文獻[3-4]針對制動缸內壓力的變化采用T-S模糊預測控制,但其文中在制動缸建模時均未考慮到輪對踏面受車體靜壓力擠壓形變和通過鋼軌接頭、道岔和不平順路段時所受的徑向沖擊形變,所用模糊規則較為復雜且壓力跟蹤性能并不理想。文獻[5]通過動力學建模及數值仿真對踏面制動器的制動過程進行分析,但在建模及控制器設計過程中未充分考慮制動缸標稱參數時變漂移及缸體內壁與活塞接觸面因非嚴格配合導致的內部壓力漏損,導致所測壓力響應時間較理論值滯后。文獻[6]采用經典PI預控列車管及風缸壓力,通過控制減壓閥閥口開度改變出口風壓,但囿于系統強非線性及時變擾動,僅通過PI控制偏差的變化已無法滿足精確控制時動態性能的要求。因此,欲滿足更為精準的動態控制和響應時間,需充分兼顧制動缸閘瓦位置控制系統中外部負載擾動(如上述車體靜壓力擠壓及不平順路段的沖擊)及內部參數攝動(如參數漂移及壓力漏損),應進行控制器變結構設計,使控制系統的輸出響應能夠滿足動態及穩態性能要求。

由于滑模控制器[7-8]可針對外部時變干擾、未建模動態及內部參數漂移進行設計,應用于非線性系統時具備強魯棒性等特點,較之于PI更具優良的動態性能。為縮短滑模面的到達時間及避免終端滑模控制輸出的奇異性,且抑制參數攝動及擾動的不利影響,本文針對制動缸閘瓦位置控制系統設計了一種基于非奇異終端滑模的自抗擾控制器,引入模糊補償因子以抑制滑模面及控制器中的奇異點跳變和未建模動態并采用帶加速度因子的細菌覓食算法(AF-BFA)進行控制器參數優化,使得控制系統在制動工況下的輸出量快速精確跟蹤給定值,并能夠克服內部參數攝動和外部負載擾動的影響。

1 基于非奇異終端滑模的自抗擾控制器設計

機車制動缸等效氣動伺服數學模型如下:

(1)

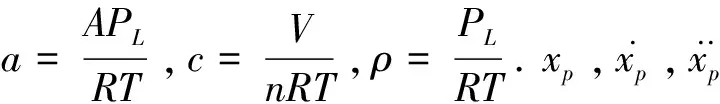
(2)

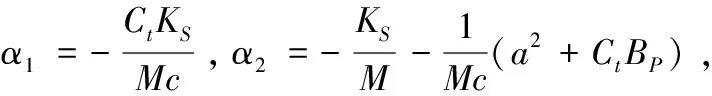
假設參考輸入xd各階導數存在,定義跟蹤誤差:

考慮各狀態變量誤差面動態,同時為縮短滑模面到達時間,設計非奇異終端滑模面為:

(3)

式中，β>0,1<γ<2,λ1,λ2>0。

定義擴張狀態觀測器:

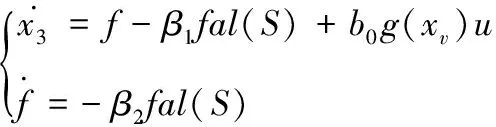
(4)

式中，f=α1x1+α2x2+α3x3+(b-b0)g(xv)u+d,

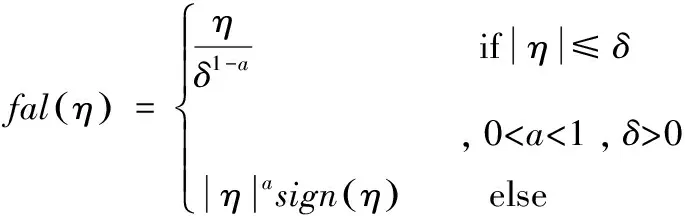
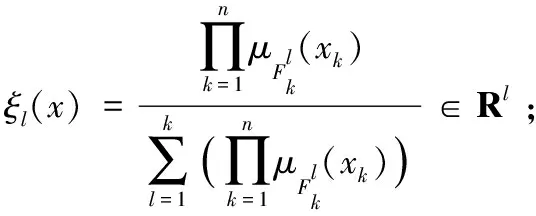
利用模糊邏輯系統[9]逼近過零攝動量,降低跳變對控制器的影響,選擇模糊邏輯逼近準則為:

(5)

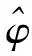
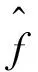
根據滑模面可達條件,結合Lyapunov方法,設計非奇異終端滑模控制器如下:

(6)

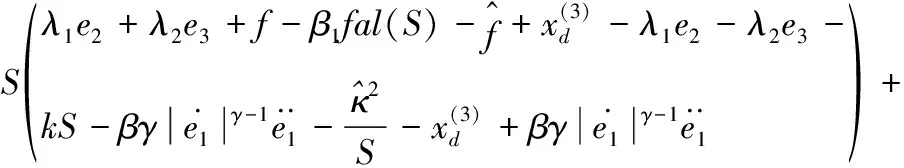
(7)

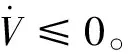
2 引入加速度因子的細菌覓食算法

本文采用引入加速度因子的細菌覓食算法(AF-BFA)對非奇異終端自抗擾控制器(NST-ADRC)參數進行優化。按照參數預選值的±10%范圍內生成初始解集,采用AF-BFA進行精確求解。在小生境生態中,細菌翻轉與游動(趨化)的方向與可覓食物濃度正相關。趨化的加速度因子表明該加速度方向上物質濃度的梯度變化程度,細菌在趨化過程中可根據各方向上加速度因子的差異選擇最優路徑快速接近食物,并按照此因子時變調節自身的移動速度。

定義加速度因子為:

(8)

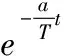
引入加速度因子的概念動態調整步長,既可在算法初期步長較小時防止過早收斂而陷入局部最優解,增強算法的初始解遍歷尋優范圍;也可在算法后期進行精確計算時,不至因步長較大而降低算法的尋優精度[10]。同時,引入服從(μ,σ)=N(0,1)的高斯分布型隨機擾動模擬小生境中的流質擾動,細菌個體受此擾動影響,概率性地跳出當前最優解,尋求覓食更優路徑。

Xi′=Xi+Xi·N(0,1)

(9)

對既得最優解進行變異替換,使之在變異條件下求算對應的適應度,若替換后最優解對應的適應度較替換前大,則認為替換后的解優于替換前的解。概率替換所得解,使之跳出局部最優區間,增進算法在較大區間內搜尋最優解的能力。

由式(4)可知,擴張狀態觀測器參數β1、β2、b0未知。為獲取滿意的過渡動態特性,降低參數關聯性影響,采用AFBFA算法對上述參數進行迭代尋優。以式(10)ITAE指標作為目標函數,引入控制量的平方項弱化振蕩,引入輸出絕對值作為懲罰項平抑超調。

(10)

式中，ey(t)=y(t)-y(t-1),y(t)為被控對象輸出,tr為上升時間,w1,w2,w3,w4為各項加權值。

3 仿真結果及分析

采用經AF-BFA優化的NST-ADRC對制動缸閘瓦位置控制系統進行仿真研究。系統制動時內部風壓流向如圖1所示。制動管向大氣排風減壓,三通分配閥活塞帶動滑閥左移,阻斷制動缸連通大氣,導通副風缸至制動缸的氣路,使得制動缸活塞受壓右移,推動閘瓦移向輪對。制動缸閘瓦位置控制系統參數見表1。

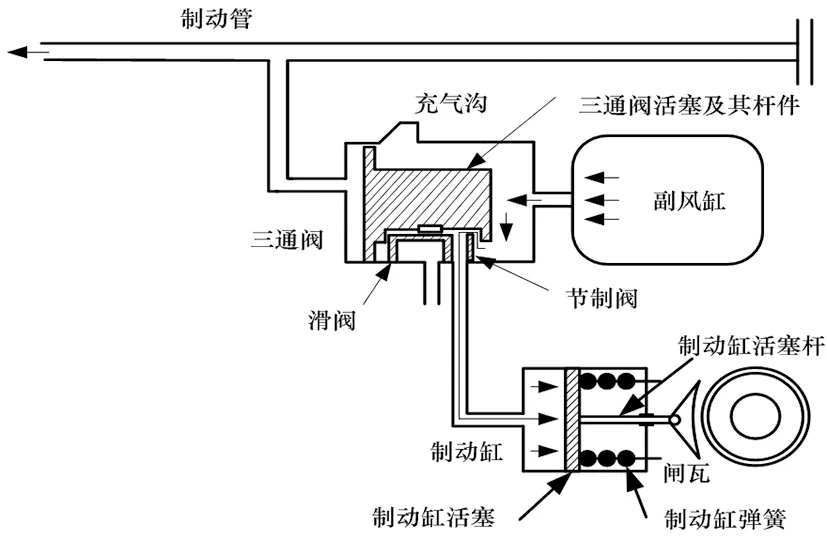
圖1 制動狀態時系統內部風壓流向

圖2為分別采用模糊PID和NST-ADRC的閘瓦位置指令跟蹤曲線。考慮實際信號存在機器讀取時間,并非階躍跳變,而是以指數形式趨近收斂于穩態,即:

xcom=xs(1-e-t/tr);式中xs=1mm;tr=0.02s

定義輪瓦接觸面反向時變作用力及系統內部標稱參數因工作點變化而產生的攝動分別為:

M′=M+0.85Msin(πt);

選取自抗擾控制器參數優化區間如下:

采用AF-BFA對上述參數進行尋優,迭代100代后得:β1=42.2143,β2=47.8336,b0=82.2194。

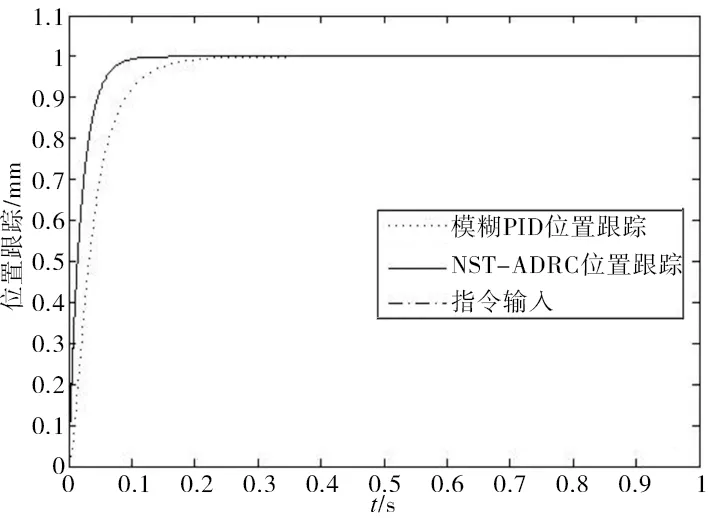
圖2 位置輸入指令跟蹤曲線

表1 制動缸閘瓦位置控制系統參數標稱值

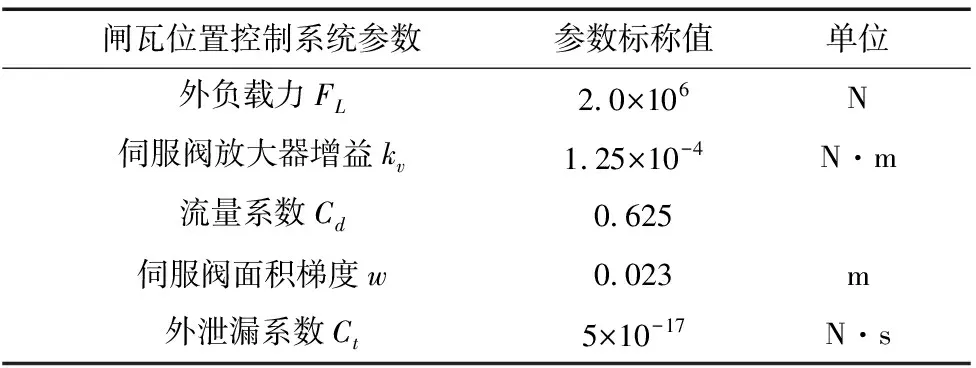
續表

由圖2、圖3可知,采用模糊PID的位置控制系統雖然能夠根據模糊規則的變化較為有效抑制擾動影響,但上升時間內由于模糊控制規則較為固定,使輸出滯后,跟蹤效果不佳(上升時間長達0.2s,跟蹤誤差最大接近0.33mm,恢復跟蹤時間接近0.2s);而基于AF-BFA的NST-ADRC針對干擾和參數時變而設計,在保證系統上升時間內對輸入指令位置跟蹤性能的同時,亦有效抵消參數攝動和外部較大擾動對系統的影響,形成近似無偏跟蹤;而調整時間內,由于采用AF-BFA算法對控制器參數進行優化,并引入模糊補償因子補償ADRC的靜差,可保證穩態無超調輸出,誤差曲線得以迅速收斂并恢復對輸入量的跟蹤。

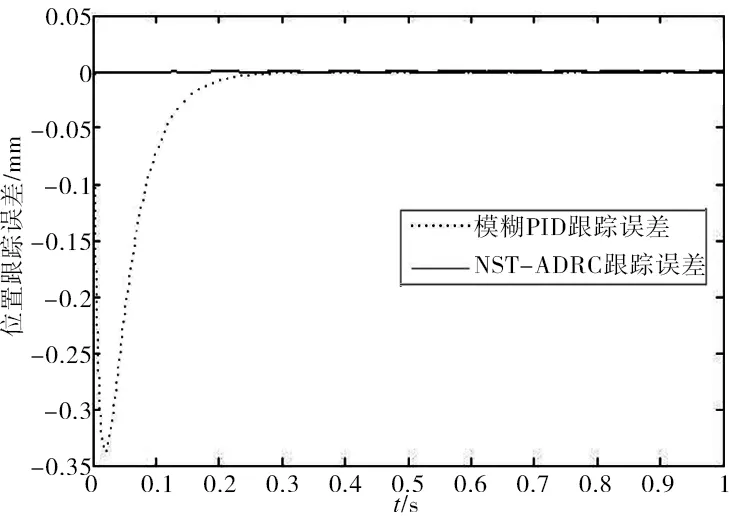
圖3 位置跟蹤誤差曲線

由圖4、圖5可知,相比于模糊PID依據模糊規則不斷調整致使控制輸入存在抖振,NST-ADRC由于引入模糊補償因子抑制和補償控制器過零點跳變和未建模動態,使控制輸入在零點附近切換平滑無抖振,且較模糊PID控制輸入曲線(用時0.12s)更為迅速終結收斂于零狀態(用時0.05s)。系統在有限時間(0.02s)內到達NST滑模面,即在有限時間內實現Lyapunov一致漸近穩定,切換面抖振較小,切換過程較為平滑。綜上所述,制動缸閘瓦位置控制系統具備較強魯棒性,可有效克服外部壓力擾動和內部參數攝動,對輸入指令實現近似無偏跟蹤。

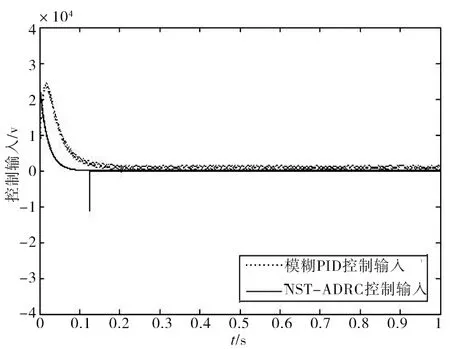
圖4 控制量輸入曲線

圖5 非奇異終端(NST)滑模面

4 結論

本文針對制動缸閘瓦位置控制系統中制動缸標稱參數漂移和內部風源壓力漏損,輪瓦接觸面受車體自重擠壓和不平順路段沖擊等實際工況,設計了基于非奇異終端滑模的自抗擾控制器。為抑制控制器在零點處的跳變和未建模動態響應,引入模糊補償因子并設計了其參數自適應律;為使控制器輸出動態性能最優,降低參數關聯性影響,采用引入加速度因子的細菌覓食算法對控制器參數進行尋優。本文設計的控制器具有優點如下:

(1)滑模面選用非奇異終端滑模,避免了終端滑模面的奇異問題,滑模面因此實現快速收斂;

(2)控制器引入模糊補償因子抑制過零跳變及未建模動態,有效降低控制器的輸出抖振;

(3)算法優化控制器參數配比,使得系統輸出更為快速精確跟蹤給定輸入;

(4)結合自抗擾控制算法,可有效抑制負載擾動和參數攝動對系統輸出的影響。

如何將本文所闡述的理論研究成果與實際工況相結合,是下一步研究的重點。