基于刀具姿態控制的指令點插補算法*

耿 聰, 吳玉厚，韓 旭

(1.沈陽建筑大學 a.高檔石材數控加工裝備與技術國家地方聯合工程實驗室；b.機械工程學院，沈陽 110168； 2.沈陽高精數控智能技術股份有限公司，沈陽 110168)

0 引言

五軸數控機床能夠通過刀尖點位置坐標和刀軸矢量的變化達到靈活控制刀具位姿的目的，從而提高加工速度、精度和表面光潔度，在航空、汽車、模具制造等行業得到廣泛應用[1-2]。指令點插補對加工精度和效率有著直接影響，是五軸數控加工中的關鍵問題[3]。

線性插補是五軸數控系統常用的指令點插補算法，該算法通過對機床各軸首末點位置坐標進行線性分割，實現刀具位姿變化[4]。在實際加工中發現，線性插補方式會導致下述問題產生。首先，五軸數控加工工件幾何造型復雜，采用直線段對復雜曲線離散化，不僅會增加數據傳輸負擔，而且在離散化過程中會產生不必要的誤差。其次，由于刀軸矢量各分量與旋轉軸位置坐標間存在非線性映射，采用線性插補法進行五軸數控加工時，無法控制刀具姿態[5]。最后，線性插補方法無法保證機床各軸速度和加速度的連續性，影響加工表面光滑度。

針對上述問題，本文提出一種基于刀具姿態控制的五軸數控加工指令點插補算法。在本算法中，刀尖點位置曲線可表示為參數樣條曲線、Bezier曲線、B樣條曲線或NURBS曲線等多種形式[6-9]，便于數據傳輸。在相關文獻[10-11]中，對平面、圓錐面刀具姿態控制方法進行了研究，本文將采用樣條曲線建立經過給定離散刀軸矢量的二階連續刀具姿態曲線，以滿足自由曲面加工中刀具姿態變化靈活多樣以及旋轉軸速度、加速度連續變化的需要。

1 算法的基本思想

采用本文所述算法進行插補時，可將五軸數控系統工作流程分為代碼預處理、刀具姿態曲線擬合、刀尖點曲線擬合和實時插補四部分，算法代碼預處理部分是后續刀具姿態曲線和刀尖點曲線擬合的基礎，該部分將讀取五軸數控程序確定刀具運動信息。數控加工程序可表示為如下格式[11]：

G05.0X_Y_Z_U_V_W_F_;

其中，刀尖點在X、Y、Z方向的坐標分量分別由X_、Y_、Z_后的數值確定，刀軸矢量在X、Y、Z方向的坐標分量分別由U_、V_、W_后的數值確定，F為該段程序對應的刀具進給速度。本算法的代碼預處理部分將讀取采用刀軸矢量編程方式形成的數控加工程序，確定刀尖點和刀軸矢量坐標。整體流程如圖1所示。

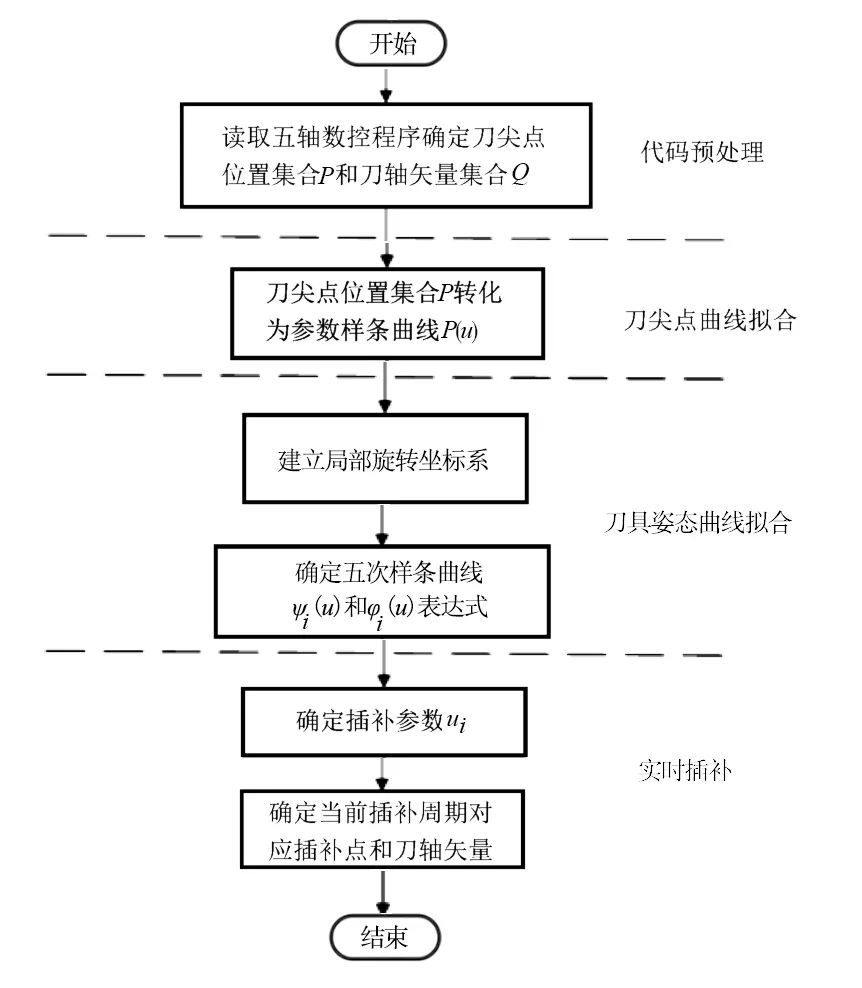
圖1 本算法流程圖

代碼預處理部分根據給定的數控加工程序得到刀尖點位置集合P={Pk|Pk=(Pxk,Pyk,Pzk)且Pxk,Pyk,Pzk∈R,k=0,…,n}和刀軸矢量集合Q={Qk|Qk=(Qxk,Qyk,Qzk),|Qk|=1,k=0,…,n}后，直接對離散刀尖點Pk和刀軸矢量Qk進行加工，會帶來機床各軸頻繁加減速問題，影響加工效率和加工表面質量[12]。為避免這一問題的產生，刀尖點曲線擬合和刀具姿態曲線擬合部分將分別對離散刀尖點和刀軸矢量進行擬合，得到刀尖點曲線P(u)和刀具姿態曲線Q(u)。

刀尖點曲線擬合部分將離散刀尖點位置集合P={Pk|Pk=(Pxk,Pyk,Pzk)且Pxk,Pyk,Pzk∈R,k=0,…,n}轉化為參數樣條曲線P(u)：

P(u)=(x(u),y(u),z(u))u0≤u≤un

(1)

其中，u為曲線參數。P(u)可表示為參數樣條曲線、Bezier曲線、B樣條曲線或NURBS曲線等多種形式。

在實際加工中發現，五軸數控機床旋轉軸速度和加速度的連續性對加工表面光潔度和加工效率等有著十分重要的影響。針對具體機床結構進行運動學分析可知，刀具姿態曲線各分量的二階連續是實現機床旋轉軸速度和加速度連續變化的前提條件[13]。因此，刀具姿態曲線擬合部分的主要功能是將代碼預處理部分得到的離散刀軸矢量擬合為二階連續的刀具姿態曲線。該部分首先根據首末刀軸矢量Q0和Qn建立局部旋轉坐標系，用與ψk和φk相關的函數表示離散刀軸矢量Qk；而后，采用三次樣條曲線近似估計ψk和φk的一、二階導數值；最后，采用五次樣條曲線進行擬合，得到經過刀軸矢量集合Q中各個離散刀軸矢量的二階連續刀具姿態曲線。刀具姿態曲線擬合部分是實現五軸數控加工指令點插補的關鍵，該部分的具體實現步驟將在下一節進行詳細說明。

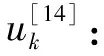
(2)

將第k個插補周期插補點對應參數值uk帶入刀尖點擬合曲線P(u)和刀軸矢量擬合曲線Q(u)，即可得到下一插補周期的插補點P(uk)和對應刀軸矢量Q(uk)。

2 刀具姿態曲線擬合

刀具姿態曲線擬合是本算法的核心。該部分通過建立局部旋轉坐標系，將單位矢量擬合轉化為角度標量擬合，通過三次-五次樣條曲線擬合得到二階連續的刀具姿態曲線，進而保證機床旋轉軸速度和加速度的連續性，下文將對其具體實現步驟進行詳細說明。

2.1 刀具姿態控制模型

在代碼預處理部分，通過讀取數控程序，可確定待插補曲線起始點P0和終點Pn對應的刀軸矢量Q0和Qn。由刀軸矢量集合的定義可知，Q0和Qn均為單位向量。根據式(3)和式(4)，可建立局部旋轉坐標系Q0-N-V：

(3)

(4)

則對于任意點Pk∈P，其對應刀軸矢量Qk可表示為：

(5)

其中，ψk是刀軸矢量Qk與刀軸矢量Q0和單位向量N所形成平面N-Q0的夾角，φk是刀軸矢量Qk在平面N-Q0上的投影與起始向量Q0間夾角，兩角度可通過下式計算：

ψk=arcsin(Qk·V)

(6)

(7)

2.2 刀具姿態曲線的確定

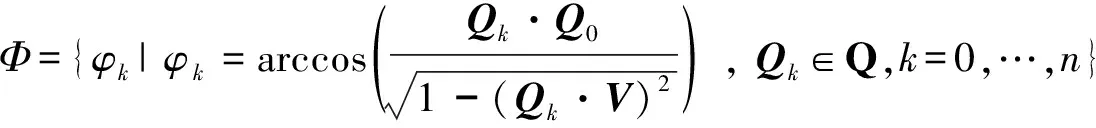
在進行曲線擬合前，首先需要確定ψk和φk對應的參數值uk，本文采用向心參數化方法確定對應參數：

(8)

其中，|Pk-1Pk|表示刀具沿Pk-1運動到Pk時的距離:

(9)

當確定ψk和φk對應的參數值uk后，將構造經過ψk和φk的三次樣條曲線，確定參數值uk對應點處一、二階導數。在此基礎上，采用五次樣條曲線構造滿足二階連續的曲線ψ(u)和φ(u)。下文將以{ψ0,ψ1,…,ψn}的擬合過程為例進行說明，{φ0,φ1,…,φn}的擬合過程類似。

假定由點ψi-2,ψi-1,ψi,ψi+1和ψi+2確定的三次樣條擬合曲線ψi(u)如下式所示：

(10)

其中，b3i,b2i,b1i和b0i是ψi(u)曲線的系數。令Ii表示點ψi-2,ψi-1,ψi,ψi+1和ψi+2與擬合曲線ψi(u)上參數ui-2,ui-1,ui,ui+1和ui+2對應點間距離的平方和:

(11)

則Ii為以bki為變量的函數，為使函數Ii達到最小值，Ii對各變量bki的偏導數應滿足：

(12)

上式可表示為:

(13)

將參數ui-2,ui-1,ui,ui+1,ui+2以及ψi-2,ψi-1,ψi,ψi+1,ψi+2代入式(13)，即可確定bki(k=0,1,2,3)的值，進而得到參數ui處對應值的一、二階導數：

(14)

參數u0和u1處對應值的一、二階導數分別等于ψ2(u0)和ψ2(u1)處一、二階導數值，參數un和un-1處對應值的一、二階導數分別等于ψn-2(un)和ψn-2(un-1)處一、二階導數值。當確定參數uk對應點ψk的一、二階導矢量后，刀軸矢量由Qk變化至Qk+1過程中，刀軸矢量與平面N-Qn間夾角ψk(u)的表達式如下所示：

其中，αk(u),αk+1(u),βk(u),βk+1(u),γk(u)以及γk+1(u) 是五次樣條曲線ψk(u)的系數：

3 實驗

為驗證本文所提出算法的有效性，將對圖2所示S型試件進行加工仿真。為便于進行分析，下文將選擇S型試件上的一條刀具軌跡進行說明，如圖3所示。

圖2 S型試件

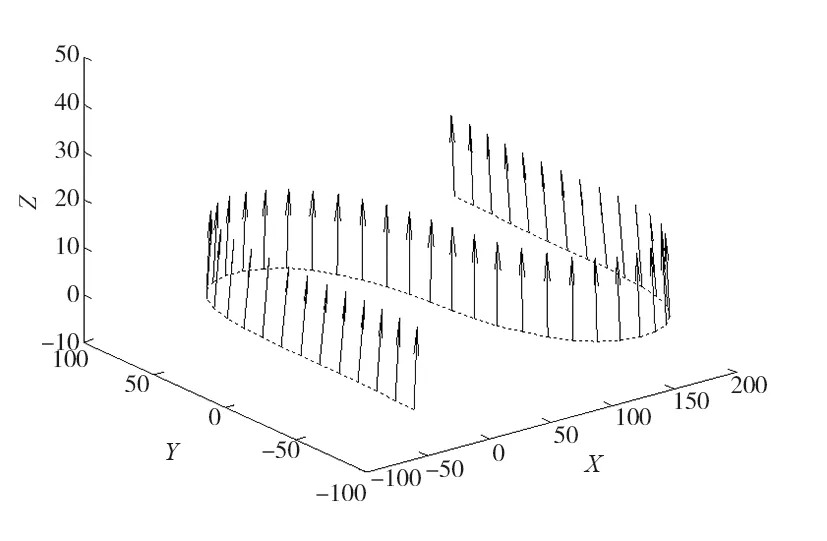
圖3 刀具軌跡

圖4所示為采用本文所述算法得到的刀具姿態曲線。由該圖可知，所得到的刀具姿態曲線位于單位球面上且經過給定的離散刀軸矢量集合，說明本算法能夠保證刀具姿態曲線上任意向量均為單位矢量。圖中星號標記點為給定的離散刀軸矢量，說明所生成的刀具姿態曲線能夠經過給定的離散刀軸矢量。

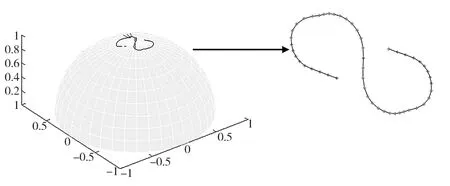
圖4 刀具姿態曲線

圖5所示為刀具姿態曲線各分量及其一、二階導數圖。該圖進一步說明采用本算法得到的刀具姿態曲線經過給定的離散刀軸矢量，且曲線在x,y和z方向各分量均滿足一階和二階連續的條件。圖6說明采用本算法得到的刀具姿態曲線進行插補時，能夠保證旋轉軸速度和加速度連續變化。

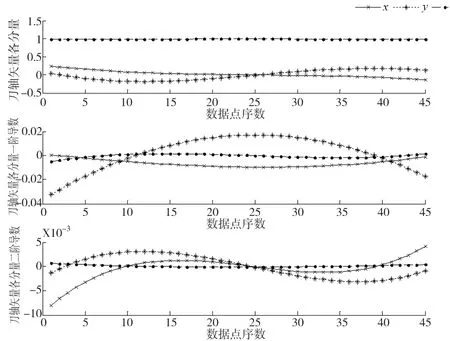
圖5 刀具姿態曲線各分量及一、二階導數變化

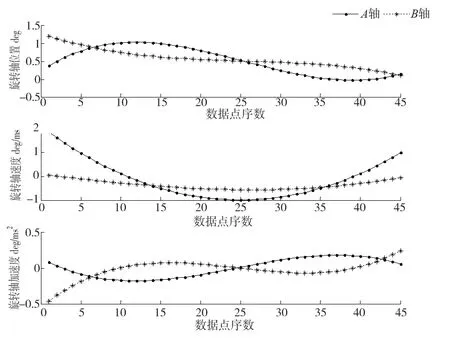
圖6 機床旋轉軸速度和加速度曲線

4 結論

本文采用三次-五次樣條曲線對離散刀軸矢量擬合得到二階連續的刀具姿態曲線，能夠保證加工中刀具經過數控加工程序確定的離散刀軸矢量序列以實現對刀具姿態的控制，豐富了五軸數控系統插補功能。基于刀具姿態控制的指令點插補算法避免了數據傳輸負擔大、刀具姿態無法控制以及旋轉軸速度、加速度不連續等問題，為提高復雜曲面整體加工效果奠定了良好基礎。