6自由度超精密線性定位系統誤差檢測與補償方法*

李文杰

(西安航空職業技術學院 航空材料工程學院，西安 710089)

0 引言

線性平臺的定位性能在精密工業領域(如生物技術、半導體技術和醫用光學)方面具有重要作用[1-2]。近年來，隨著光學和電子等技術的快速發展，對其精密線性系統的定位精度要求也逐漸提高[3]。定位精度受多種因素影響，大體可以分為幾何誤差、熱誘導誤差源、切削力誘導誤差源及其它誤差源等。

為實現超精密定位，需要消除這些誤差源產生的不精確性。從自由度角度分析誤差源可以得到6個自由度相關的誤差，分別是3個平移誤差和3個旋轉誤差。通常可以通過離線法對定位誤差進行測量，以提高定位平臺的定位精度。近年來已有相關研究學者對不同自由度線性平臺誤差源進行研究，并應用各種測量設備測量線性平臺的不同自由度相關誤差[4-5]。但是，設備性能很大程度上影響了測量結果的準確性。因此，誤差測量過程中需要利用最佳傳感器以提高測量精度。雙球桿可以用來研究幾何誤差的影響，但是該方法無法分辨出誤差的具體類型，同時球桿的分辨率也比其他測量系統的分辨率低[6]；激光干涉儀測量幾何誤差最精確，但是可適用性較差、耗時長[7]。

另一方面，目前已有的研究所提出的精密定位平臺都是針對微位移范圍內提高運動定位精度。因此，對于較大行程的線性平臺位移運動難以實現誤差補償。同時，已有的相關研究需要對外部測量系統的定位和旋轉運動進行控制，不同納米定位系統的結構或測量系統會對不同自由度誤差補償產生限制[8-9]。并且，之前的研究主要集中在特定誤差源產生誤差的測量與補償方面，例如幾何誤差和熱誘導誤差等主要誤差源。但是，這些離線補償方法在最小化幾何誤差時是有用的，由于其時變誤差源的特點故不適合用于熱誘導誤差或動態誤差。

基于以上研究，本文提出一種6自由度超精密線性定位系統，并對該精密定位系統幾何誤差、熱誘導誤差以及動態誤差進行測量并實時補償。該系統采用剛度高、響應速度快的并聯柔性鉸鏈機構，通過對該定位平臺動力學進行分析，針對提高定位系統性能提出遞歸補償算法；最后對比誤差補償前后的實驗結果，分析均方根誤差和峰谷值誤差，用來驗證該裝置的有效性。

1 6自由度超精密定位平臺的設計

1.1 系統設計

線性平臺能夠提供大的工作空間和快速的加速度。本文所提出的6自由度超精密定位系統安裝在線性平臺上，其原理如圖1所示。通過壓電驅動器對多自由度柔性機構進行驅動可以實現較高分辨率。線性系統坐標系與末端執行器坐標系之間關系恒定，與機床指令無關，見下式：

(1)

6自由度超精密定位平臺裝置如圖2所示。驅動組件包括基準平臺、移動平臺、6個壓電驅動器以及6個柔性關節。壓電驅動器位于基準平臺和移動平臺之間。由于并聯機構的特點，驅動元件結構剛性強，響應速度快。兩自由度關節與移動平臺項相連，3自由度關節與基準平臺相連。因此，驅動組件可以實現6自由度運動(三平移三旋轉)。5個電容式傳感器和參考鏡作為測量工具測量幾何誤差、熱誤差以及動力學誤差。傳感器采集的數據用于對精密平臺5自由度誤差進行補償(兩平移誤差和三旋轉誤差)。補償算法和旋轉運動驅動工作臺保持最終的目標位置。

圖1 微納定位平臺原理

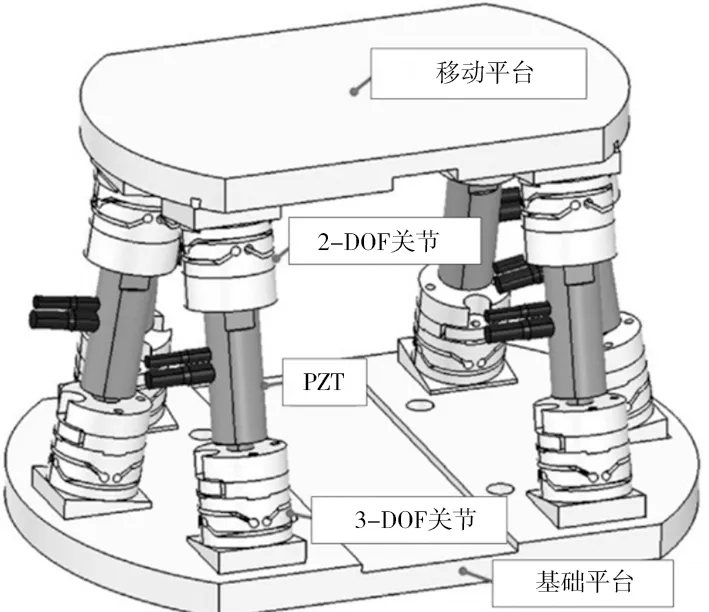
圖2 6自由度超精密定位系統結構圖

1.2 動力學分析

測量和驅動坐標系統用于識別運動平臺的中心和定義參考坐標系，通過Abbe誤差的最小化實現對誤差的精確測量和補償。用逆運動學方法計算補償特定誤差所需要的壓電驅動器位移Δli(i=1,2,3)，運動平臺{M}、基準平臺{B}以及關節{i},{j}的坐標系統定義如圖3所示。

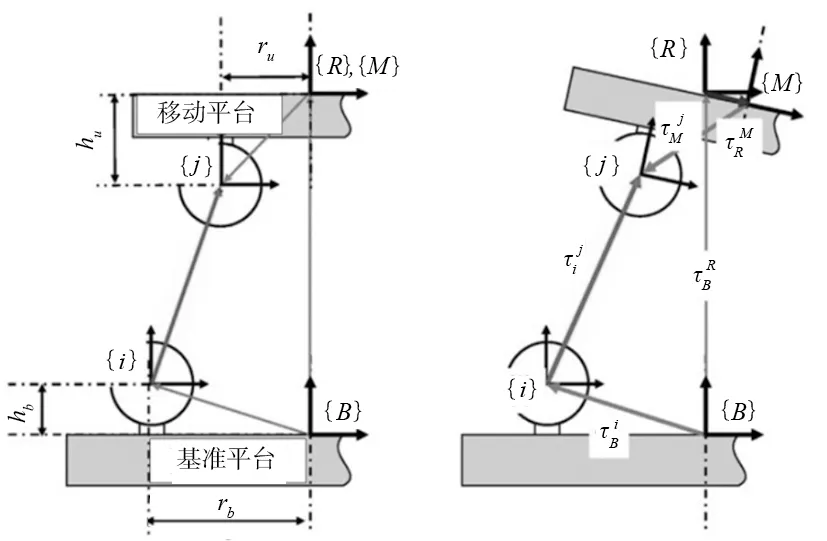
圖3 動力學反解坐標系統

參數hb和rb分別表示基準平臺{B}和關節{i}關于基準平臺上的高度和半徑。同樣地，參數hu和ru分別表示相對坐標系統{M}和關節坐標系統{j}關于移動平臺上的高度和半徑。其中關節坐標系統{i}和{j}通過運動鏈進行確定，見式(2)。利用齊次變換矩陣對系統剛性部分的運動進行建模，其中R和P分別表示關節坐標系{i}相對于{j}的旋轉矩陣和位移矢量。

(2)

式(2)中具體參數計算如下：

P=(xyz)T

(3)

并聯機構受工作空間大小的限制，柔性關節的使用大大降低了工作空間的大小。因此，工作空間分析要求運動可行性驗證，利用正向運動學方法計算了動平臺的位姿和壓電陶瓷的位移。定義兩個平臺坐標系統中每個關節的速度為ai,bi(i=1,2,...,6)，計算壓電驅動器的位移，表示為di(i=1,2,...,6)。采用高斯-牛頓方法，結合式(4)和式(5)計算位移與6自由度誤差之間的關系。其中，壓電驅動器范圍為±7.5mm。

(4)

(5)

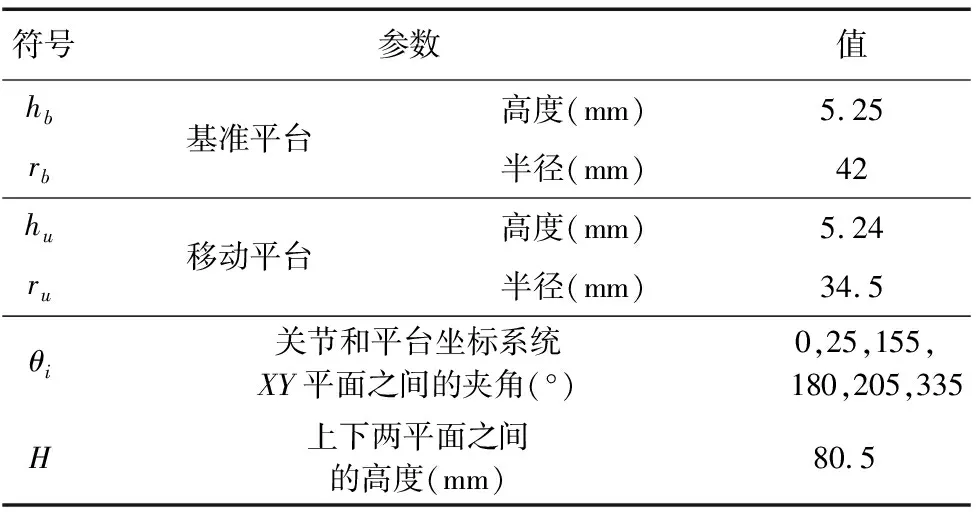
表1 納米定位平臺設計參數

2 誤差測量及補償

如圖4所示，利用參考平面鏡和5個電容式傳感器對線性平臺5自由度誤差進行測量。在運動參考鏡和5個電容式傳感器條件下，位置誤差的標準不確定性顯著增加。因此，使固定在傳感器位置上的末端執行器沿軸向移動，并根據傳感器測得的數據估計幾何誤差。參考坐標系統用來定義測量和驅動坐標系識別移動平臺的中心和傳感器的位置si(i=1,2,...,5)。參數l,h和w分別表示傳感器距離、高度以及寬度。利用式(6)計算測量數據mi(i=1,2,...,5)，其中下標表示不同傳感器編號：

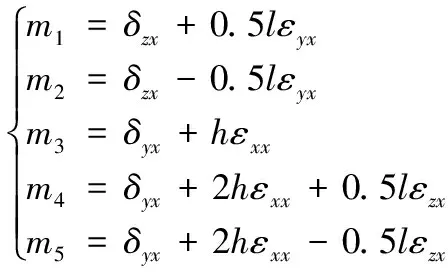
(6)

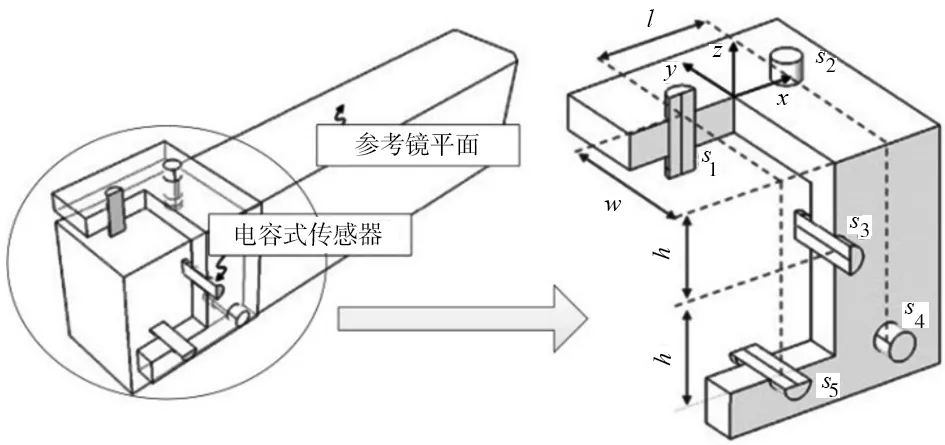
圖4 誤差測量裝置

測量數據的標準不確定度直接受到基準面平面度和傳感器性能(線性度和分辨率)等不確定因素的影響。因此，為了評價測量結果的可靠性，對測量設備的不確定度因素進行了分析，并計算測量數據的標準不確定度。用測量數據的標準不確定度評定了5自由度誤差的標準不確定度。本文通過設置傳感器與參考坐標系之間的最佳關系，測量出5自由度誤差的標準不確定度。

利用傳感器si(i=1,2,...,5)得到的數據計算5自由度誤差和各傳感器數據與幾何誤差的關系，見式(7)。因此，可以對驅動軸{X}上兩位置誤差(水平直線度誤差δyx和垂直直線度誤差δzx)和三轉動誤差(旋轉誤差εxx、俯仰εyx和偏轉誤差εzx)進行計算。估計誤差可用于逆運動學建模和壓電驅動器位移Δli計算。因此，6自由度定位機構中運動平臺沿固定參考鏡的恒定姿態直線進行運動。

(7)

除了前面所討論的誤差外，雙伺服系統的制造誤差和裝配誤差也影響到直線軸的精度。為此提出誤差補償算法進行補償以提高定位精度。理想坐標系統{X}i應遵循參考坐標系{R}的x軸，但是實際坐標系統{X}a會發生偏離。位置μ包括6自由度運動(三平移和三旋轉運動)，本文中由于系統可以對線性平臺5自由度誤差進行測量，所以μ表示兩平移和三旋轉運動，如式(8)所示：

μ=(δxxδyxδzxεxxεyxεzx)T

(8)

補償的過程就是使實際位置的坐標系統{X}a應與理想坐標系統{X}i重合，但由于雙伺服系統的制造和裝配誤差，以及幾何、熱感應和動態誤差等時變誤差，使得兩個坐標系的匹配變得復雜。因此，采用臨界運動Δμi(i=1,2,...,n)進行i次補償得到補償后的補償坐標系{X}ith，見式(9)：

Δμi=(δiεi)T

(9)

式中，δi=(δxx,iδyx,iδzx,i)T，εi=(εxx,iεyx,iεzx,i)T。

進行i次補償后，μ+∑Δμi對剩余運動Δμi(i=1,2,...,n)進行補償。當殘余運動Δμi(i=1,2,...,n)在公差范圍內時，迭代過程就完成了。因此，雙伺服系統根據給定的公差控制坐標系對實際坐標系統{X}a進行匹配，具體補償流程圖如圖5所示。通過動力學反解計算壓電驅動器特定運動位移Δli(i=1,2,...,6)，通過測量的運動來計算的補償值，以滿足公差內的剩余運動Δμi(i=1,2,...,n)，本文中設定公差值為60nm。

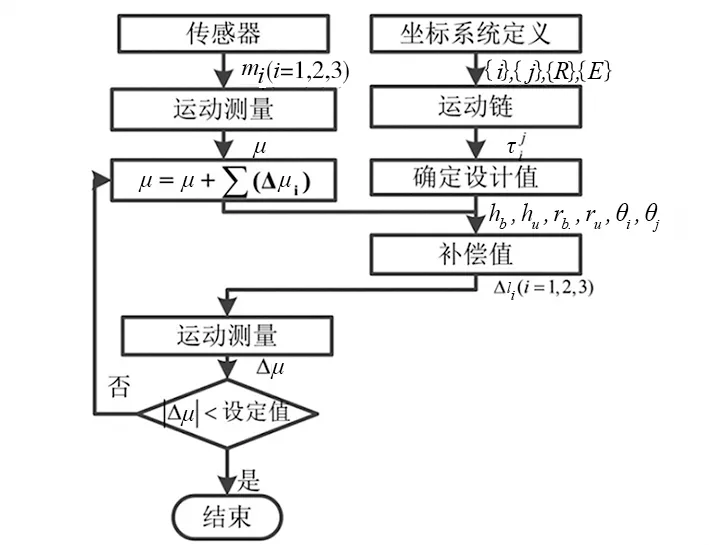
圖5 補償算法流程圖

3 實驗

為便于獲得所需要的關節尺寸，采用高精度電火花線切割加工的方法制備納米定位平臺的柔性關節。其中電容式傳感器、壓電驅動器和參考平面鏡參數如表2所示。由于受參考平面鏡大小的限制，整個系統設置為寬100mm、長80mm、高78.5mm。參考鏡由微晶玻璃制造，不受熱誘導引起的誤差影響。驅動器組件安裝在線性軸上，固定參考鏡以最小化Abbe誤差。

用LabVIEW軟件對5自由度誤差進行實時測量和補償，補償算法對壓電驅動器位移Δli(i=1,2,...,6)進行計算。用激光干涉儀對電容傳感器和參考鏡測量結果的有效性進行了驗證。當使用激光干涉儀測量定位誤差時，必須考慮Abbe誤差以進行精確測量。因此，激光干涉儀的測量坐標系與補償機構末端執行器的基準坐標系相匹配，以盡量減少測量系統之間的Abbe偏移。具體測量結果如圖6所示。由圖6a和圖6b可知，基于6自由度定位系統提出的誤差測量系統計算得到的平移誤差和旋轉誤差測量結果與激光干涉儀實際測量結果相吻合，兩個測量方法之間的最大差值在數據的可重復性之內。另外，隨著定位系統線性軸向位置的增大，旋轉誤差逐漸減小，表明該系統適用于具有較大行程的定位。因此，驗證了實驗中所使用的測量系統有效性。平移運動的峰谷誤差值為2.17μm，轉動誤差為8.22rad/s。

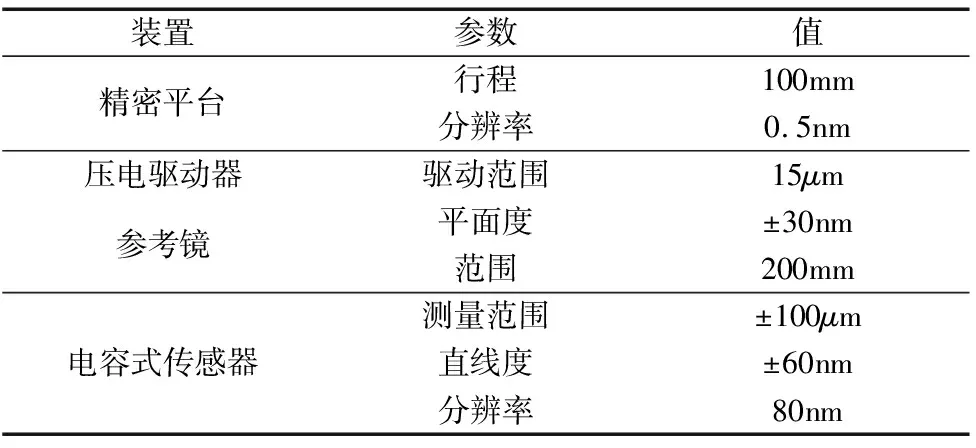
表2 實驗裝置參數

(a)平移誤差

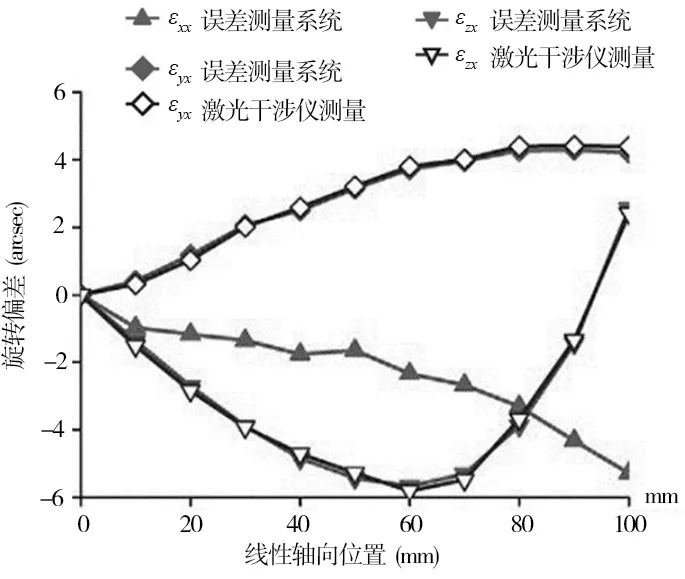
(b)旋轉誤差圖6 誤差測量系統驗證對比實驗

精密平臺的5自由度誤差補償前后對比結果如表3所示。在實驗結果中，補償后位置誤差和旋轉誤差的PV值分別降低到7%和5%。位置均方根誤差和旋轉均方根誤差分別減少了91%和96%。動態條件下的實驗結果與穩態結果相比有增加的趨勢。然而，RMSE和PV在理論的公差范圍(±0.2弧秒的旋轉運動和±50 nm的位置運動)。因此，驗證了本文提出的誤差補償算法的有效性。

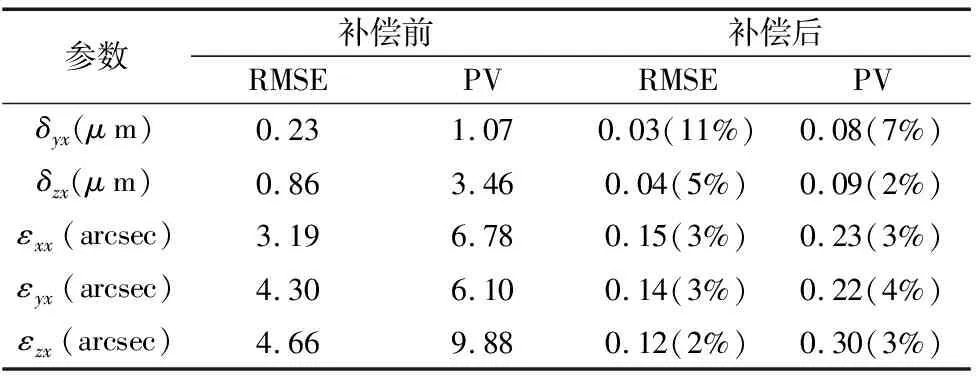
表3 誤差補償結果

4 結論

本文提出一種6自由度線性超精密定位系統。該系統可以實現期望的線性定位同時能夠對幾何誤差、熱誘導誤差和動態誤差引起的6自由度誤差進行實時補償。補償機制采用柔性鉸鏈來獲得超精密定位，同時采用聯機構，具有結構剛度高、響應速度快等特點。通過對工作臺的運動學進行動力學分析，提出基于遞歸技術的補償算法，提高了系統的定位精度，并通過實驗驗證了測量系統和補償算法的有效性。