基于反向傳播神經網絡的白車身在線監測*

屈 原，何金蓉，秦成輝，劉暢輝，金 隼

(1.上海交通大學 上海市復雜薄板結構數字化制造重點實驗室, 上海 200240；2.上汽通用五菱汽車股份有限公司, 廣西 柳州 545007)

0 引言

在線測量系統的廣泛應用能夠更為有效、快捷和準確的實現車身焊裝過程中各種故障(夾具、焊接、工藝參數變化等)的檢測[1]。車身質量問題故障所對應的制造尺寸的偏差問題粗略地可以分為兩種，一是均值漂移，二是尺寸波動。其中，均值漂移帶來的偏差問題通常可以通過質量工程師在車間內調整夾具而快速地解決，而真正對車身裝配質量更為影響顯著的是相對難以控制的波動因素。在車身尺寸偏差質量控制過程中，尺寸方差的控制成為難點，也是白車身質量控制的核心所在，因此，如何針對方差變化進行有效的監控是目前在線監測亟需研究的問題。

多年以來，人們一直在研究如何利用具有實時性的在線測量數據對白車身制造過程進行智能化監控。美國Michigan大學胡仕新[2]等人最早采用時間序列分析對在線測量數據進行處理分析以快速準確地監測車身尺寸均值漂移，取得了良好的效果，但是對其他諸如均值漸變以及方差的模式預測并沒有展開進一步研究。Hu和Wu[3]運用主成分分析方法對100%的在線測量數據進行分析，提出了兩級故障分類模式，結合專家知識系統可以快速定位偏差源，在實踐中成功地降低了車身的裝配偏差。在此基礎上，Geglark[4]結合了主成分分析白車身產品和工藝知識，對裝配過程進行有效地故障診斷。

在企業實際使用過程中，依靠質量工程師人為地對在線測量數據控制圖中出現的異常模式進行查看和判定，需要消耗大量的人力，并難以適應高速運行的生產線節拍，亟需一種智能的模式識別自動監控方法。人工神經網絡具有非線性、自學習、自適應等優點，是一種有效的模式識別方法。國外一些學者利用人工神經網絡對控制圖進行模式識別，取得了不錯的效果。Pham和Ozteml[5]嘗試使用神經網絡對控制圖的均值階躍、均值趨勢和循環變化進行了有效識別。Cheng[6]研究了神經網絡的結構，閾值的選取以及不同的學習訓練方式在識別效率上的影響。李宏光，李丹[7]提出廣義神經網絡對對象模型數據進行離線訓練，對上升階躍和下降階躍的異常模式進行識別，并在TE(Tennessee Eastman Process)化工控制過程中取得了應用。張祥敢等[8]針對BP網絡的激勵函數提出改進，加速了神經網絡的收斂速度，同時采用實際加工過程的設計尺寸生成四種類型的樣本數據，包括正常、趨勢、階躍和周期，更好地代表了實測數據。并以軸類零件加工過程控制圖為例，驗證了BP網絡對控制圖的復雜模式具有不錯的識別效果，但對于特征的選擇沒有深入的研究。

總結以上文獻，應用神經網絡進行在線監測是一種有效的方法。然而目前針對模式識別的研究主要以均值為研究對象，應用領域以加工制造為主，較少涉及裝配過程中的方差異常模式。因此，本文針對白車身在線監測的實際測量數據，構建了波動異常模式仿真函數(方差階躍和方差漸變)，并在此基礎上建立三層反向傳播BP神經網絡，為白車身焊裝車間經常出現的波動異常在線監測探索一條新途徑。

1 基于BP算法的人工神經網絡建模

1.1 BP神經網絡算法

反向傳播(Back Propagation，BP)算法是一種有監督的學習算法，它的實質是通過計算網絡的實際輸出和期望輸出之間的誤差，并且按照梯度減少的方向來修正網絡節點的權值和閾值，以此來達到實際輸出和期望輸出的誤差最小的目的[10]。下面對BP算法的原理以公式的形式做簡單介紹：

假設BP網絡的輸入層(Input layer)、隱含層(Hidden layer)和輸出層(Output layer)分別由NI、NJ和NK個神經元。可以算出隱含層第j個神經元的輸入為：

(1)

式中，wij是輸入層第i個神經元到隱含層第j個神經元的連接權值；權值的初始化為隨機選取一個比較小的值。在這里Oi為輸入層中第i個神經元的輸出。

同樣的，輸出層第k個神經元的輸入為：

(2)

式中，wjk是隱含層第j個神經元到輸出層第k個神經元的權值；Oj為隱含層第k個神經元的輸出。

輸出層的輸出為：

Ok=fk(Ik,θk)

(3)

式中，θk為輸出層第k個神經元的節點閾值。fk(·)表示S型激活函數。

網絡的平均誤差為：

(4)

式中，Tpk表示輸出層第k個神經元的期望輸出；Opk表示這個神經元的實際輸出。

BP算法通過不斷調整神經元的權值和閾值的方式進行學習，最終的目標是使誤差函數取得最小值，以滿足實際使用的要求。

輸出層的權值通過以下公式進行調整：

Δwjk(n+1)=ηδpkOpj+αΔwjk(n)

(5)

(6)

式中，η為學習速率，α為動量因子。學習速率過大會導致整個系統不穩定，容易產生振蕩現象；反之，則會導致訓練時間的增加，使得整個系統收斂變慢。

隱含層的權值通過以下公式進行調整：

Δwij(n+1)=ηδpjOpi+αΔwij(n)

(7)

(8)

閾值的調整同理。

1.2 方差仿真函數

為了更加有效地對白車身焊裝質量進行智能監控及診斷，本文借鑒西方電氣公司提出的6種控制圖模式——正常模式、趨勢模式(向上和向下)、階躍模式(向上和向下)和周期模式，構建了白車身焊裝車間裝配過程的波動異常模式仿真函數(方差階躍和方差漸變)，公式如下：

x(t)=0.5×r(t)+k×1.0×r(t)

(9)

x(t)=0.5×r(t)+b×1.0×r(t)

(10)

式中，階躍前b=0，階躍后b=1，分別代表階躍前和階躍后；k是斜率，根據大量在線實測數據以及現場質量工程的經驗，這里選取為0.05。在MATLAB數值分析軟件中以樣本容量為60繪制圖形，如圖1所示。

圖1 方差異常模式

特征提取是模式識別的前提，通常也被稱為數據的預處理。簡單地采用原始數據進行模式識別，往往會因為數據中包含噪聲使識別精度降低，同時也會因為樣本數據維度大造成計算耗時過長。因此如何選取合理的特征成為決定模型好壞的關鍵。

借鑒文獻[11]，選取參數SB、AASL、SRANGE和REAE作為形狀特征統計量，這些形狀特征與均值和方差的取值無關聯，使得模式識別具有較好的一般性。分別以參數AASL、SRANGE和REAE為X、Y和Z坐標，根據蒙特卡洛仿真出200組數據繪制三維圖，如圖2所示，可以發現選取的三個特征能夠很好的區分出方差漸變和方差階躍。同時為了體現出方差漸變的微小趨勢，把60個數據分為6段計算均值和方差，得到12個統計特征，再加上偏度、峰度以及均方差共計19個特征量，作為神經網絡的輸入矢量。

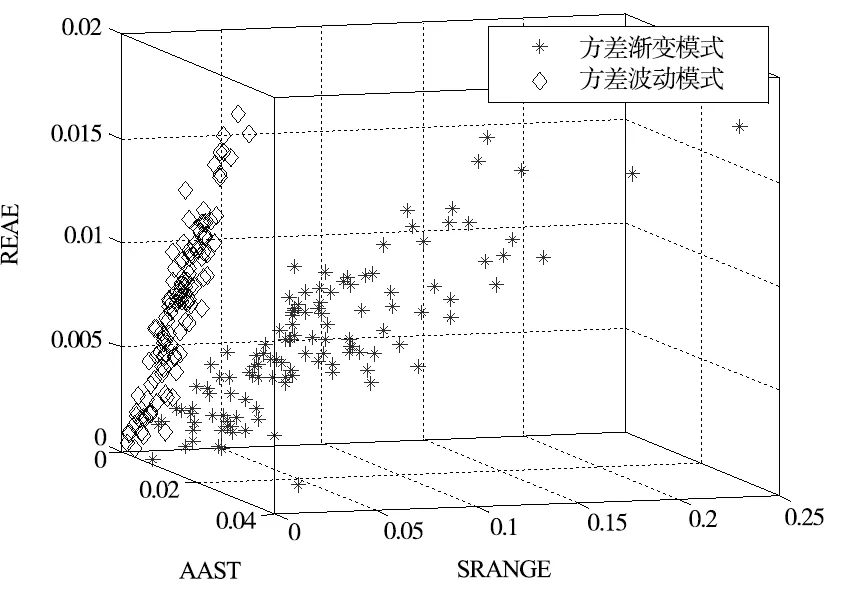
圖2 AASL,SRANGE,REAE分布圖

1.3 神經網絡模型建立

根據神經網絡理論，隱含層節點數選取過多，會造成學習時間很長。反之，網絡的魯棒性不好，抗噪聲能力差。通過多次比較不同隱含層節點數的訓練結果，最終確定隱含層節點為15。即白車身焊裝車間在線監測模型結構為19-15-7。

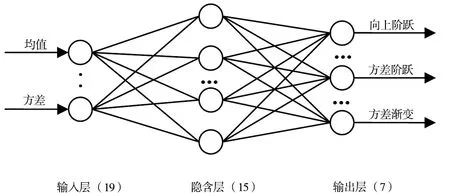
圖3 白車身在線監測BP網絡模型

隱含層的轉移函數采用連續可微的logsig函數。為了確保網絡的輸出限制在[0,1]之間，輸出層的轉移函數采用purelin函數，并采用compet競爭輸出。網絡的訓練采用trainlm函數，實際測試表明，trainlm函數計算比traingd函數要快很多。網絡的允許的最大訓練步數為2000步，并且每隔100步顯示一次訓練結果。經過反復試驗，學習速率設置為0.05。

2 人工神經網絡的訓練和驗證

由于白車身的測點公差存在±1.0、±1.2和±1.5三個等級，計算得出的19個特征在幅值上存在差異，所以在輸入到神經網絡之前，需要對所有的輸入參數做歸一化處理。

網絡的輸出為向上趨勢、向下趨勢、向上階躍、向下階躍、方差階躍、方差漸變、正常模式7種模式。

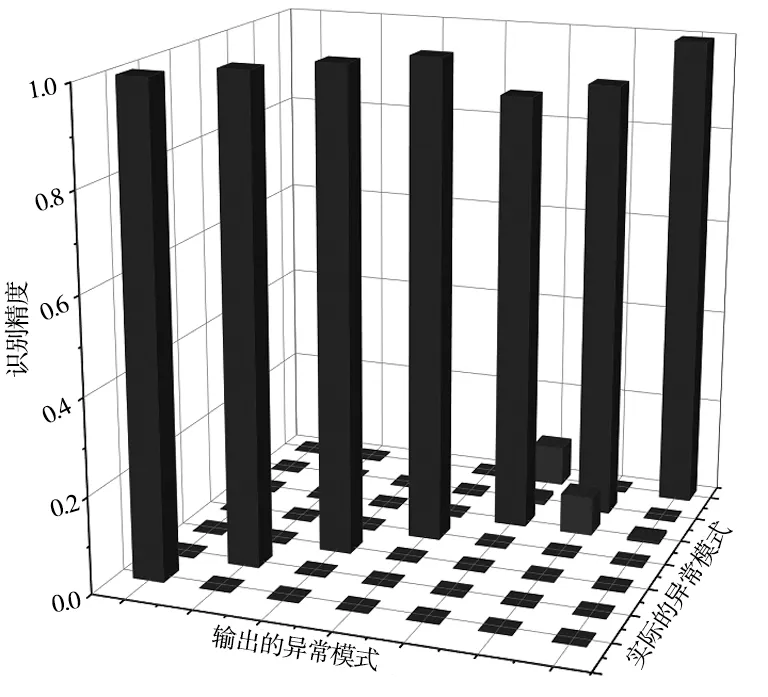
圖4 模式識別精度對比

針對每個模式采用蒙特卡洛仿真出120組數據樣本，隨機選取其中的20組作為訓練樣本，其余作為測試樣本。

神經網絡訓練結束后，利用測試樣本對網絡進行驗證，得到的神經網絡模式識別和實際模式如表1所示。對于前四種的均值模式均可以達到很好的識別精度，訓練好的網絡可以達到100%。但是對于方差的兩種模式，尤其是對于比較微小的方差階躍，識別精度有所下降，準確率為90.8%。對于方差漸變模式的識別準確率為91.7%，并且還可以發現，兩種波動模式之間容易存在混淆，大約有9%的誤判率。該網絡模型在測試集上的對于7種模式的平均識別準確率為97%。

3 案例分析

將上述方法應用于工程實際中，以某車型的前車架區域為例，24號測點為該車型前懸減震器安裝點，測點的偏差影響到前輪定位參數，進而影響到汽車的行駛穩定性、乘坐舒適性以及安全性。因此有必要在實際生產過程中作為關鍵測點進行監控，這里以該測點CPF(17-24R)的Z方向即高度方向的變化為研究對象。

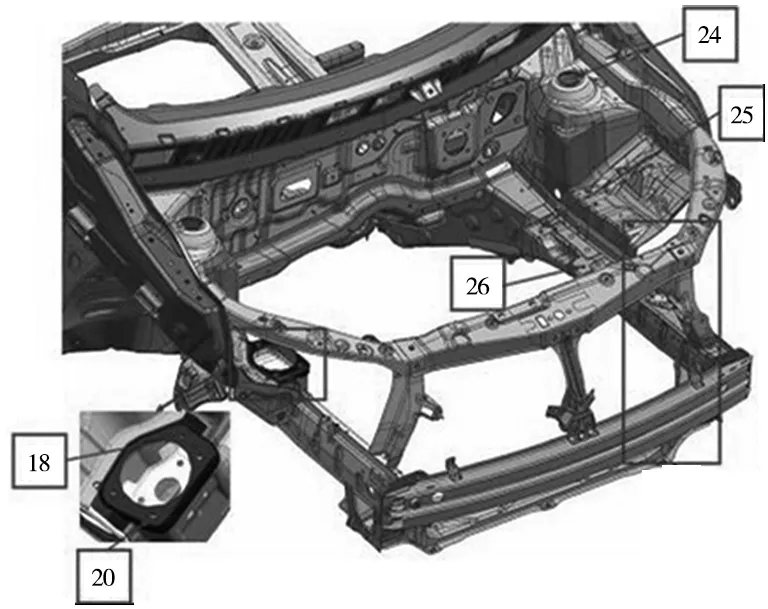
圖5 前車架

選取該測點的500臺車在線測量樣本，如圖6所示。將用于取值的監控窗口設置為60，同時設定步長為1。每次讀入一個新的數據，同時舍棄最早的舊數據，使窗口內的數據長度保持為60個。

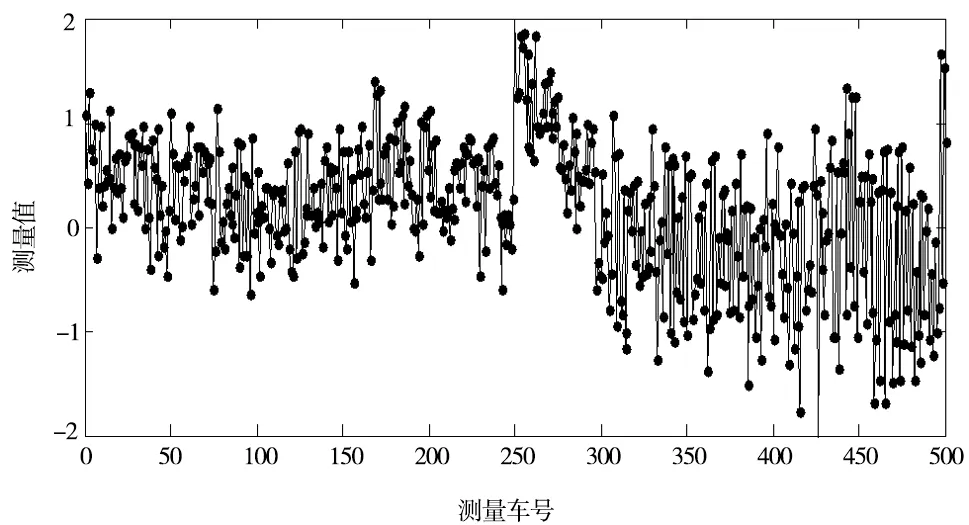
圖6 實測數據

采用訓練過的神經網絡模型對監控窗口內的數值序列進行特征提取和模式識別，并輸出識別的結果如圖7所示。可以看出，在這段實測數據中不存在模式1向上階躍和模式3向下階躍，因此這里僅選取模式2-7為縱坐標。在這段過程中，前200臺車的輸出模式為7，對應的是正常模式；在第204臺車，開始輸出模式3，對應的是向上階躍模式，通過及時響應，控制部分不合格零部件的尺寸偏差。在第225臺車，生產狀態重新回到正常；在第250臺車，開始輸出模式2，對應的是向下趨勢模式；在第278臺車，開始輸出模式5，對應的是方差階躍模式，并且在區間[380，430]反復報警。在第385臺車，開始輸出模式6，對應的是方差漸變模式。此時該測點的方差波動較大，相對與前半段變得不穩定，質量工程師應及時響應排查故障原因。

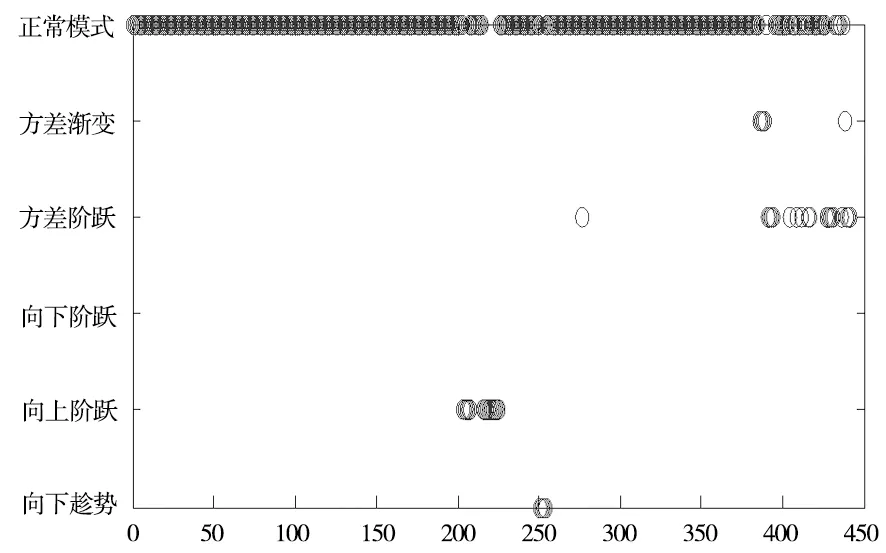
圖7 輸出模式類型

通過與實際的控制圖曲線相比較，并與質量工程師的專家經驗和生產線的夾具調整記錄相匹配，驗證了所提出的方差階躍和方差漸變模式能夠快速地反映生產線的實際波動狀態，更好地發揮在線監控的作用。

4 結論

提出了方差異常模式的仿真函數構造方法，建立了白車身異常模式監測的BP神經網絡模型，并將某車型實際測量的數據代入模型進行驗證，結果表明該模型可以對方差異常進行有效監控，并具有較高的準確性，能夠有效代替人工識別。為白車身焊裝車間的質量診斷提供依據，該方法也適用于其他存在波動異常的自動化生產過程的在線質量智能監控。