數形結合思想方法在高中數學解題中的應用

一、數形結合思想方法的應用原則

在高中數學解題中，數形結合思想方法的應用要堅持以下幾點原則：一是等價原則。二是雙向原則。三是簡潔原則。四是直觀與創新原則。

二、數形結合思想方法的應用策略

（一）以形助數，使抽象問題變得形象直觀

在高中數學解題中，特別是對于一些數量關系既復雜又抽象的問題，學生難以理解，不容易找到解題的思路和方法。如果運用數形結合的思想方法，就可以把復雜抽象“數”的問題用直觀的圖形問題來解決，這樣就可以繞開冗長煩瑣的數量計算的過程，利用圖形能夠幫助學生有效解決復雜的數量問題，使學生對題目中的數量關系能夠正確理解， 即能夠把題目中抽象的數量問題變成形象直觀的圖形問題，可以使學生容易理解題意，快速準確地找出已知條件、未知關系，快速形成解題思路，快速正確地找出數量關系式，從而有效突破解題難點。

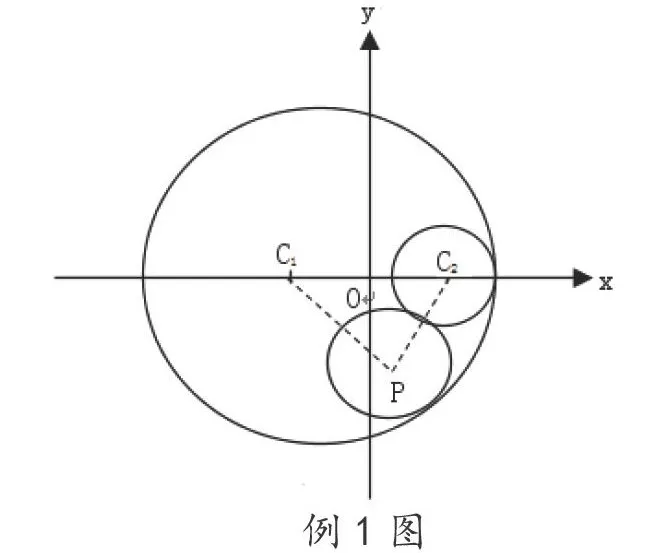
例1：已知一個動圓P與兩個定圓相外切，定圓C1方程是：（x+4）2+y2=100， 定圓C2方程是：（x-4）2+y2=4，求這個動圓P的圓心軌跡的方程。

解析：此題的解答如果直接運用求解方程的方法會非常麻煩，而如果運用數形結合的思想方法，通過借助于兩個圓圖像的“形”來求方程“數”的問題就比較方便。假設動圓的圓心為P（x，y），半徑是r，從方程可以得出：定圓C1的圓心是（-4，0），半徑是10;定圓C2的圓心是（4，0），半徑是2。借助圖形可以直觀看出：動圓C與定圓C1是相內切的，與定圓C2是相外切，就能容易得出下面的式子：|C1P|=10-r，|C2P|=r+2，把兩個式子相加得：|C1P|+|C2P|=10-r+ r+2=12>|C1C2|=8，根據橢圓的定義可知點P的運動軌跡是橢圓。再根據圖形可得出c=4，a=6，可求出b2=20， 動圓P的圓心軌跡的方程是x235+y220=1。

點評：在本題的求解中，借助于圖形的直觀性，通過做輔助線的方式，很快就能形成解題思路，使問題既簡單又快捷地得到解決，很好地體現了“以形助數”的思想。

（二）以數解形，使學生的解題思維更嚴謹

數學作為一門非常嚴謹的學科，在進行數學知識學習或解題時必須要有嚴謹的思維能力，許多學生在解題時，不夠嚴謹，經常會粗心大意，造成解題錯誤或找不到正確的解題思路。如果學生在解決一些比較復雜的圖形問題時，借助于“數”的嚴謹性與精確性，來找出圖形中包含的數量關系，以此來解決幾何圖形問題，既容易找到解題思路，又能培養學生嚴謹的思維能力。而且對于一些幾何圖形問題，有時候如果僅憑直覺觀察不容易找出圖形的特點和規律，借助于“數”的精確性，就能深入細致地刻畫圖形，能深入挖掘幾何圖形中的隱含條件，使解題更加嚴謹。

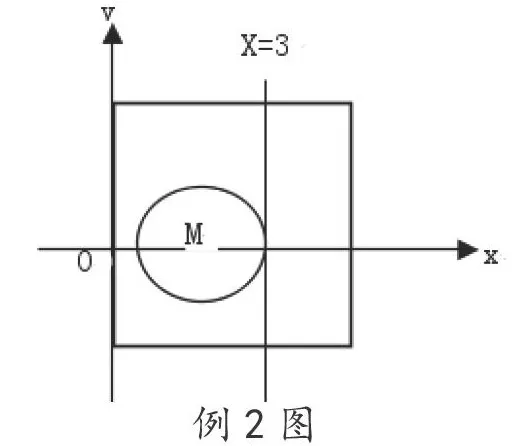
例2：有一個圓M介于直線x=3和拋物線y2=2x所圍成的封閉區間里（含邊界區域），求這個圓M在此區域中能取得的半徑最大值是多少？

分析：從圖形中可以大概看出圓半徑的數值，但無法得到精確的圓半徑數值。如果借助于代數的嚴謹、精確的計算，就能求出準確的圓半徑數值。可分兩種情況進行討論：第一，不含邊界時。 當圓M在這個封閉區域中不含直線和拋物線邊界時，即圓M與直線和拋物線均不存在交點時，無法用聯立方程組的形式進行求解;第二，包含邊界時。當圓M在這個封閉區域中包含直線和拋物線邊界時，即圓M與直線和拋物線均存在交點時，可用聯立方程組的形式進行求解。根據圖形可看出：圓M的圓心在x軸上，因此假設其圓心為（a，0）（0<a<3），這樣可得圓的方程是（x-a）2+y2=（3-a）2，把圓方程與拋物線方程聯立組成方程組，可得x2+21-ax+6a-9=0，?=[2（1-a）]2-46a-9=0，再結合a的取值范圍，就可求出a=4-6，因為3-a<a，因此，最大半徑是3-a=6-1。

點評：要精確求解本題，關鍵是要用“數”的嚴謹性與精確性來求解圓半徑，即要用“數”來輔助求解“形”的問題。此外本題容易忽略3-a<a這個條件，這樣圓M就可能超出該封閉區域。

三、結語

總之，數形結合思想能夠幫助學生形成完整的數學知識體系，能夠把復雜抽象的問題變成形象直觀、容易解決的問題，能促進學生思維能力發展，因此，教師應在教學中注重滲透數形結合的思想方法，從而提高解題質量效率。