控制量權重可變的主動段最優中制導律*

馬自茹，魏明英，李運遷

(1.北京電子工程總體研究所，北京 100854；2.中國航天科工集團有限公司 第二研究院，北京 100854；3.空天防御創新中心，北京 100854)

0 引言

現代戰爭中，彈道導彈無疑是威脅最大的一種武器，所以對彈道導彈的高精度攔截就顯得尤為重要。彈道導彈的飛行一般分為3個階段，主動段，中段和末段。主動段攔截，從攔截效果上來看是最理想的，但是需要克服的困難也很多，需要的外界條件很難達到，所以現代的防空導彈，都以中段或末段攔截為目標。無論是中段攔截還是末段攔截，都普遍采用復合制導的方式，整個制導過程分為初制導，中制導和末制導。其中，中制導需要達到的制導目標是最復雜的，需要滿足的約束是最多樣化的。

一般來說，末制導的初始條件就是中制導的制導目標[1]。為了保證中末制導可靠地交班，保證最終命中目標，對中制導段提出3方面的要求：①控制導引頭測量軸指向目標，其控制誤差不應超出彈上測量裝置的視場范圍；②導彈與目標的距離應在導引頭的測量范圍之內；③導彈的速度應滿足末制導的初始要求。除此之外，在實際中，對于中制導還有著很多其他的要求。首先，現在的防空導彈，多是主動飛行與被動飛行相結合，并且使用攔截器直接碰撞的攔截方式，這就要求導彈在飛行的過程中保留足夠的動能，要求控制能量盡可能小。此外，對于一些靜不穩定度比較大的導彈，當攻角比較大，過載比較大的時候，容易使姿態徹底失控，所以對于這類導彈，要求整個飛行過程中的過載盡可能的小。傳統中制導常采用比例導引的方法，這種方法在制導精度上可以滿足要求，但是無法引入更多的約束，其過載曲線往往峰值較大，變化劇烈，相應的，控制能量損失也很大。

目前，很多中外論文都將最優控制理論應用于中制導律的解算當中。文獻[2]基于E-Guidance理論[3]，給出了一種最優制導律，實現將導彈從初始狀態控制到預測的末位置，滿足最終速度傾角約束，同時滿足使導彈速度最大的優化目的。但是這種方法得到的結果，形式復雜，而且很難直接應用到實際的仿真程序中。文獻[4-5]采用最速上升法求解2點邊值問題，但是直接求解2點邊值問題計算量大，難以在彈上實時完成，文獻[5]設計了一種帶角度約束的制導律，但是并沒有考慮導彈速度的變化率，對于主動段飛行的導彈來說，速度變化率是不可忽略的一個因素。文獻[6]所要解決的問題與本文是類似的，同樣是在中制導末端滿足速度的角度約束，但是對于控制量的約束，僅僅限于在指標函數中使控制能量最小，而沒有做更多的改進，在仿真驗證中，這種導引律的實際過載在飛行前期較大。文獻[7-14]雖然研究對象不同，但是在解算方法上都是類似的，但是在建立的指標函數中，控制量的權重依然是1或者常數，這就使得在解算出控制量算法后，無法再對控制量的大小進行調整。文獻[15]給出了一種使用時變控制量權重的高斯偽譜法，說明時變的控制量權重的可行性。

本文研究的問題是，在導彈飛行的主動段，考慮導彈速度變化率，將導彈控制到預測點，使末位置誤差盡可能小，同時滿足末速度傾角約束，滿足視線角變化率趨向于0，并且導彈過載更小。為了滿足以上約束，本文將所有約束條件統籌到一個指標函數當中，通過極小值原理解算控制量的解析形式。為了使飛行中的過載更有可控性，變化更平緩，整體更小，采用在指標函數中加入可變控制量權重的辦法，這種方法得到的制導律，可以通過調節控制量計算式中的參數來實現對不同階段過載大小的控制。分別給出了離散式和解析式算法的推導過程。

1 導彈運動模型

建立導彈的運動模型。將導彈的運動分解為橫向和縱向，先研究縱向平面的運動，如圖1所示。圖1的坐標系，是以導彈和目標點連線所在的平面為坐標系的Oxy平面，而在實際的仿真模型中，這個坐標系不是標準坐標系之一，所以要進行坐標變換。圖1中，M0為導彈的初始位置;Mf為導彈的飛行目標點;v0為導彈的初速度;vf為導彈的末速度;θ0為導彈的初始速度傾角;θf為導彈的末狀態速度傾角，也是控制目標;q為導彈到目標點的視線角;R為相對距離。則，在縱向平面內，導彈飛向目標點的運動模型為

(1)

2 最優制導律

2.1 狀態方程和指標函數的建立與解算

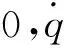
θ(t)=q(t),

(2)

所以，在末位置時，如果滿足

q(t)-θ(tf)=0,

(3)

則同時滿足

θ(t)-θ(tf)=0.

(4)

(5)

是一種很理想的交班情況。

對于一個最優控制問題，建立狀態方程是很關鍵的步驟，需要把約束條件涉及的變量設為狀態變量，決定了使用最優理論解算的目標，同時也決定了解算過程的繁復程度以及是否能夠得到解析解。有一些簡單的狀態方程類型是可以得到解析解的，雙積分系統就是其中之一，這里在建立狀態方程時，建成了雙積分系統的形式。

對式(1)中間等式求導運算：

(6)

式(6)結合式(1)可得

(7)

根據之前敘述的約束條件，取狀態量為式(8)形式

(8)

則有系統狀態方程式

(9)

根據前文分析，為了在接下來的解算中，更容易得到解析解，這里通過引入偽控制量的辦法，將系統形式寫成雙積分系統。令

(10)

則有新系統

(11)

考慮約束條件，列寫指標函數。這里要考慮的約束有，系統2個狀態變量的末狀態，控制量盡可能地小。所以有指標函數式

(12)

直接將控制能量的比重r陣取為1。而c1，c2的取值由末狀態約束決定。

對于這種雙積分系統，針對式(12)形式的指標函數，利用極小值原理可以得到解析解，這個過程已經為人們熟知[6]，這里不做詳細介紹，直接給出結果。

(13)

約束要求，x1(tf)=0，x2(tf)=0，則c1和c2→∞，則式(13)可轉化為

(14)

(15)

2.2 最優導引律的改進，可變權系數的指標方程解算

一般的二次型指標函數形式為

(16)

u(t)=-r-1(t)BT(t)K(t)X(t),

(17)

式中：r與u(t)為求逆關系。總之，當r取比較大的值時，也就是說，控制量在指標函數中所占比重較大，而求解的目標是使指標函數取極小，則控制量的值會比較小。

使用最優導引律的彈道，前期過載大，變化劇烈，后期過載小，變化平緩，希望能對其改進，實現前期和后期的一種平衡，對前期進行抑制，而后期則進行放大。這就要求改變r的形式，使前期控制量在指標函數中的比重較大，后期在指標函數中的比重較小。設新的指標函數為

(18)

這里r由常數陣改成了時變陣，已經不適合于上文中給出過的解的形式，需要另行推導。有2種方法可以解決這個問題，一個是離散的方法，另一個是根據極小值原理直接推導。前者推導容易實現，但是在應用中要求的計算量大，后者推導難度大，但是在應用中要求的計算量較小。

下面給出，針對系統(11)和指標函數式(18)，利用極小值原理的解析解解算過程。將式(16)寫成

(19)

根據式(19)和系統方程，漢密爾頓方程為

(20)

根據極小值原理，寫出橫截條件，終值條件和控制方程

(21)

觀察控制量的形式，發現欲求控制量，必須先求λ2。這里有的是，λ2的一階導數和末值，理論上肯定可以求解，直接解算的結果中會包含x1(tf)，x2(tf)2個量。

(22)

式(22)可得

λ2(t)=λ2(tf)+c1tg(t)x1(tf)=

c2x2(tf)+c1tgx1(tf),

(23)

代入控制量的表達式

u(t)=-tg(t)-nc2x2(tf)-tg(t)-n+1c1x1(tf).

(24)

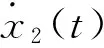
(25)

由式(25)可算得

(26)

因為

(27)

所以積分可得

(28)

根據式(27)和(28)可以解算x1(tf)，x2(tf)，如果直接解算，由于每項的系數很復雜，容易出錯，這里將其設為

(29)

根據式(27)，(28)，(29)可以計算得到

(30)

前文敘述，約束要求2個狀態末值為0，所以取c1和c2→∞。將式(30)代入式(24)可得

(31)

因為在建立指標函數的時候，用的是r(t)=tg(t)n，這樣雖然解算過程稍微復雜一些，但是卻具有普適性，n的取值不同，可以達到不同的優化目的。當n>0的時候，前期控制量在指標函數中的比重大，后期小，這樣可以實現使前期過載較小，后期過載較大的優化目的，而當n<0時正相反，可以實現前期過載較大，迅速縮小與控制目標的偏差，而后期則過載較小，這也是具有應用意義的，比如，對于一些直接針對目標的制導問題，越到飛行后期，需要過載的大小對目標的機動的反映就越明顯，所以希望在飛行前期盡快縮小偏差，而后期的過載盡可能小。

3 仿真驗證

仿真程序考慮全彈氣動力、萬有引力、發動機推力、控制系統包含、制導部分、控制部分、導航部分。其中，本文推導的制導律主要編入制導部分。在導航基準坐標系中，初制導結束時，即主動段中制導開始時的狀態為已知，即位置，速度，彈道傾角和彈道偏角皆已知，控制目標為，預測點xf，yf，zf，以及彈道傾角和彈道偏角的期望值。

主要針對彈道傾角，即縱向進行制導控制。注意，在前文中建立的導彈運動模型，是將導彈的縱向運動平面放置在Oxy平面內，這種坐標系并不是常用的幾種坐標系定義，所以需要在導航坐標系的基礎上進行坐標系變換，將導航基準坐標系的Oxy面轉到導彈縱向運動的平面內，即繞y軸轉一個彈道偏角即可。

分別針對原有制導律(theoriginal)，最優制導律(qtheta)和可變權系數制導律進行仿真驗證。主要關心的數據為，彈道傾角終值與目標值的差，導彈y向過載大小，彈目視線角變化率的歸零快慢，位置誤差。

3.1 彈道傾角變化

將原有制導律，最優制導律和可變權系數制導律的2種情況的彈道傾角變化曲線繪制在圖2中，根據曲線可以發現，原有制導律的快速性較差。而當n取正值或者負值時，可變權系數制導律的曲線分別在最優制導律的上側和下側，這也印證了前文的理論推測。

幾種制導律的彈道傾角末值與期望值的偏差如表1所示，單位為rad。

表1 制導律的彈道傾角末值與期望Table 1 Trajectory inclination terminal value and expectation of guidance law rad

可以發現，最優導引律的精度最佳，其誤差在0.004以內。

3.2 過載變化

將這些導引律的過載變化曲線分成2組進行對比，第1組對比theoriginal和qtheta，意在分析最優方法解算出導引律與其他方法的不同，第2組為包含qtheta和可變權系數導引律，這是對最優導引律的改進，意在表現改進的效果。

第1組如圖3所示，發現原本的導引律，過載峰值大，變化劇烈，而且后期存在連續抖動，對于一些靜不穩定度大的導彈，這種過載曲線是很不理想的。以最優理論推導出的導引律，如前面所預測的那樣，前期峰值大，變化劇烈，但是后期較小且變化平穩，這種導引律是精度最高的。

第2組如圖4所示，這一組主要是用來分析對最優導引律的改進效果，其他曲線都與qtheta進行對比分析。可變權系數的方法推得的導引律是比較理想的，這里分別取n=1和n=-1，試驗證明，當n=1時，前期的過載得到了抑制，后期由于在程序里使用限幅模塊，即當精度達到要求之后，就領導引律計算結果為0，所以在這里體現的并不明顯。n=-1的導引律在前期過載較大，變化劇烈，但是從圖1中可以看出，這樣的大過載增加了快速性，使傾角很快的就達到了目標值附近。但是付出一倍多的過載增大是不值得的。

4 結束語

本文針對復合制導中的主動段中制導，將導彈導引至目標點并滿足角度約束的問題，考慮導彈的速度變化率，建立了導彈的運動模型。根據給出的約束條件選擇狀態變量建立了系統狀態方程。使用最優理論推導了導引律，仿真試驗證明，使用最優理論的導引律精度最高，過載大小和變化的劇烈程度均優于原有導引律，而且在推導過程中加入的約束都滿足。試驗證明，最優理論是解決多約束中制導問題的有力工具。

而后對最優導引律提出了改進方案，可變權系數法，需要重新用極小值原理推導算法，給出了離散法和解析法2個結果。仿真試驗證明，可變權系數的方法達到了預期的效果，當n取不同值時，其對控制量有不同的限制，這種方法和思路在其他中制導過程和末制導中也會有很大的發展空間，本文證明了這種想法的正確性。