柯西不等式在初等數(shù)學(xué)物理中的若干應(yīng)用

徐浩然

（安徽省合肥市第一中學(xué)高二（26）班，安徽 合肥）

法國(guó)著名數(shù)學(xué)家柯西，1789年8月21日出生于巴黎。他對(duì)數(shù)論、數(shù)學(xué)分析、抽象代數(shù)和微分方程等多個(gè)數(shù)學(xué)領(lǐng)域進(jìn)行了深入的研究,并取得了許多重要成果。著名的柯西不等式就是其中之一。此不等式在初等數(shù)學(xué)的解題中應(yīng)用上具有耳目一新、靈活巧妙的作用。有些參考書上采用了構(gòu)造函數(shù)、利用判別式的方法來(lái)證明。而本文在此給出了三種更為簡(jiǎn)捷的證明法：引入了二次型法和數(shù)學(xué)歸納法，來(lái)證明柯西不等式。

定理 1 設(shè) ai，bi為任意實(shí)數(shù) i=1，2，…，n則，

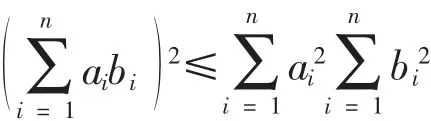
其中等號(hào)當(dāng)且僅當(dāng)ai，bi成比例時(shí)成立。（柯西不等式原命題）

1.證明方法

方法1（簡(jiǎn)潔證明）

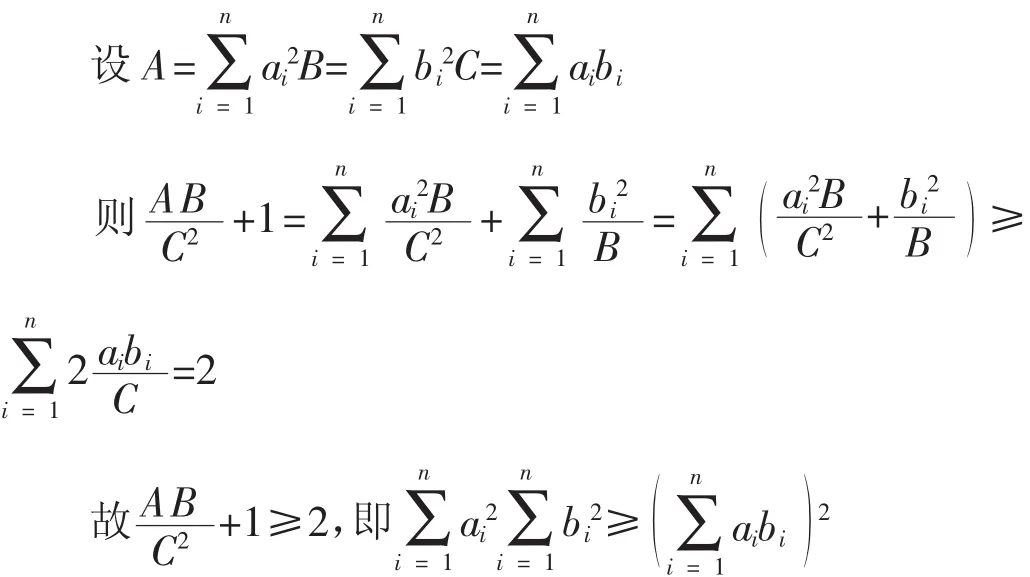
方法2（二次型法）

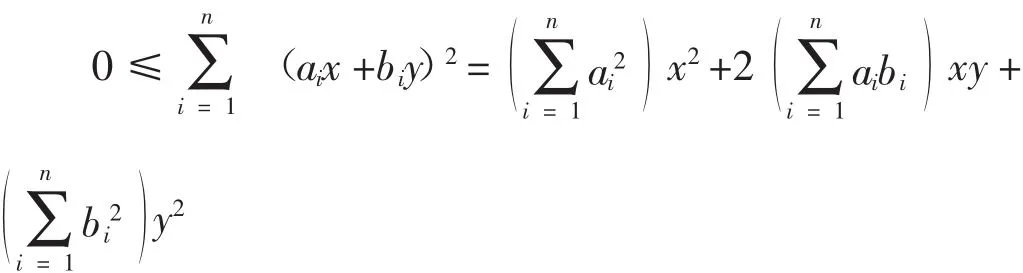
由常識(shí)可知，上式的二次型是關(guān)于x與y的非負(fù)函數(shù)，故有

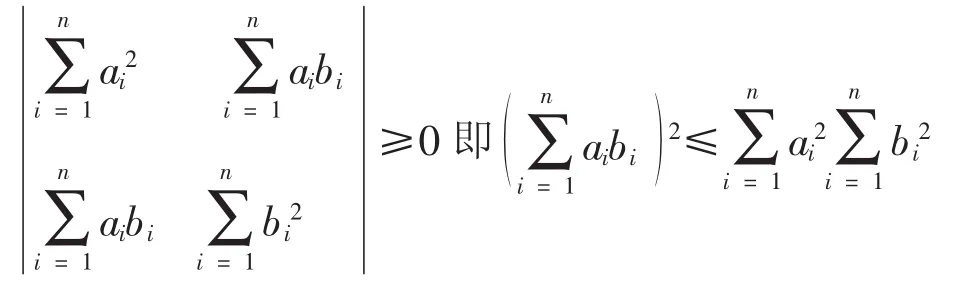
成立

證明方法3（數(shù)學(xué)歸納法）

當(dāng)n=1時(shí)顯然成立

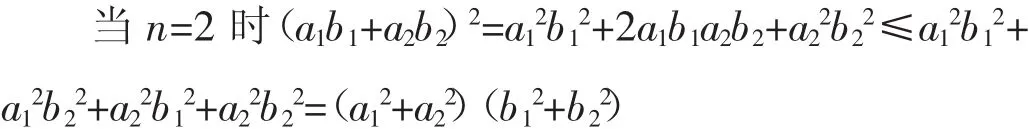
其中的等號(hào)當(dāng)且僅當(dāng)a1b2=a2b1時(shí)成立

那么當(dāng)n=k+1時(shí)

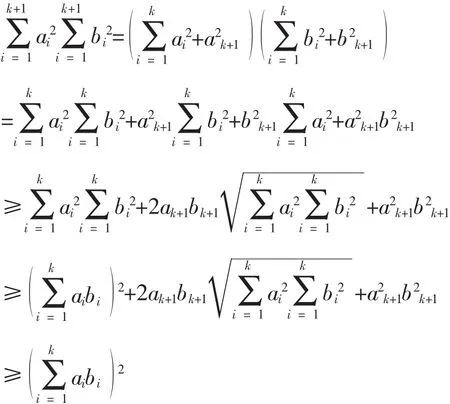
其中等號(hào)當(dāng)且僅當(dāng)aibj=ajb（ii，j=1，2，…，k）時(shí)成立。

二、柯西不等式的簡(jiǎn)單應(yīng)用

柯西不等式是一個(gè)非常重要的不等式，學(xué)習(xí)柯西不等式可以提高我們的數(shù)學(xué)探究能力、創(chuàng)新能力等，能進(jìn)一步開(kāi)闊我們的數(shù)學(xué)視野，培養(yǎng)我們的創(chuàng)新能力，提高我們的數(shù)學(xué)素質(zhì)。在合適的場(chǎng)合，靈活巧妙地運(yùn)用它，可以使一些使用平常方法不易解開(kāi)的難題迎刃而解。這個(gè)不等式結(jié)構(gòu)寬松，應(yīng)用靈活廣泛，常通過(guò)適當(dāng)配湊，直接套用柯西不等式解題，常見(jiàn)的有兩大類型：

例1 已知正數(shù)a，b，c滿足a+b+c=1。求證：a3+b3+

證明：利用柯西不等式：

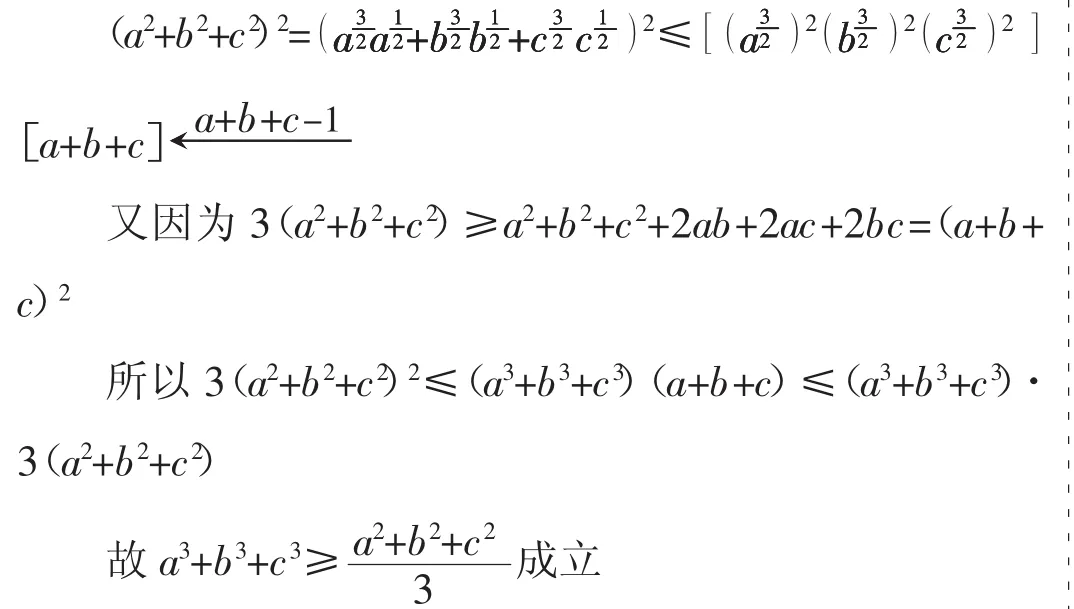
例2 三角形外接圓問(wèn)題

設(shè)P是△ABC內(nèi)部的一點(diǎn)，x，y，z是點(diǎn)P到三角形三邊a，b，c的距離。……