變式教學策略在廣州數學中考復習的實踐與體會
張小青
(廣東省廣州市從化區城郊中學,廣東 廣州)
一、了解中考命題的方向與特點
教師要認真研究近幾年廣州中考試題,了解試卷中會出現哪些題型,在不同的題型中又會考查哪些知識和能力,了解命題的趨勢。中考題源于課本的例題或常見題再加以變式得到,加大了對學生解題能力考查,注重知識運用和遷移。例如:
(2017 年廣州中考)20.如圖,在 Rt△ABC 中,∠B=90°,∠A=
(1)利用尺規作線段AC的垂直平分線DE,垂足為E,交AB于點D。(保留作圖痕跡,不寫作法)
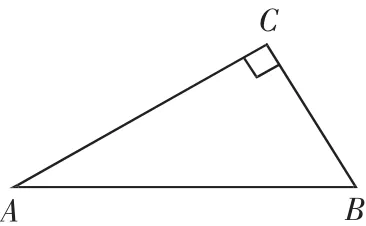
(2)若△ADE 的周長為 a,先化簡 T=(a+1)2-a(a-1),再求 T的值。
上面的化簡求值題考查了整式或分式的化簡,再結合方程、不等式組、函數或幾何圖形計算等已知條件進行求值,凸顯了雙基的運用、代數與幾何的綜合。
二、中考復習課存在的問題
復習課上老師較喜歡運用“滿堂灌”的教學模式,認為自己講得越多、越細,學生對知識就能掌握得越好。還有的教師把復習課上成練習課,做一題講一題,沒有帶領學生分析題目考查內容和考查意圖,更沒有引導學生歸納問題的解題思路和解決方法。這樣的復習課堂上容易出現以下情形:一是大多數學生復習課上處于盲目隨從狀態,思考得少。二是課堂氣氛沉悶。三是學生之間的交流幾乎沒有。這樣何來有好成績呢?所以,每位初三數學教師都要認真思考“用什么方式上中考復習課才能高效?”“怎樣調動學生積極思考?”其實,在中考復習中,題不在于多,在于典型性和針對性。哪怕簡單的題也可能蘊含著重要的數學思想方法,要深入挖掘題目內涵,讓學生融會貫通,拓展知識深度,這往往比一節課做很多題更有效。
三、變式教學的界定
變式既是一種重要的思想方法,更是一種行之有效的教學方式。那什么是變式?變式是指變更事物的非本質特征以突出本質特征的不變,或變更事物的本質特征以突出非本質特征的不變,但這些變更所得的不同表現形式與原有事物之間要保持一定相似。而變式訓練就是教師通過變式方式進行技能和思維的訓練,變式教學就是采用變式方式進行的教學。
變式教學要有效,必須遵循以下幾點原則:
1.目的性:圍繞本節課的教學目標,有目的地進行變式設計,不能為變而變,不能讓學生感覺到是在炒冷飯,要讓學生在復習舊知時也能收獲新知,能激發學生學習的欲望。
2.針對性:在復習過程中,教師對練習題的選取要有針對性,切忌隨意選題,特別是復習之初,選題不能太難,也不能太易,應根據學生的實際情況,結合知識模塊的重難點來選擇練習題的變式訓練題。
3.參與性:因為學生在知識、技能、能力、興趣上都會存在一定的差異,教師在教學中要考慮學生的差異性。因此,教師所設計的變式題目要有層次性、梯度性,盡量使每個學生都能夠參與其中。
例如:
1.當代數式a+b的值為3,代數式(a+b)-4的值是 ( )
A.5 B.6 C.7 D.8
2.已知 x-y=5,則(x-y)2-4(x-y)+4=________ 。
3.已知 a+b=5,a-b=2,則 a2-b2=______。(提示:將 a2-b2分解因式)
4.已知 x2+y2=17,xy=4,求(x+y)2和(x-y)2的值。(提示:將所求代數式先化簡再代值)
5.已知(x+y)2=25,(x-y)2=9,求 xy,x2+y2的值。
6.如圖,長方形的長和寬分別是 a、b,如果 a、b 滿足(a+b)2=8,(a-b)2=3,求這個長方形的面積。
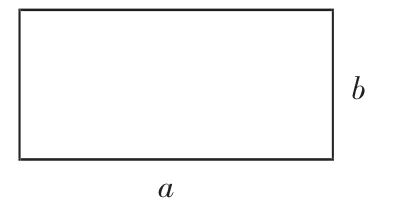
以上題組訓練是對含完全平方式、平方差的式子進行化簡求值,是根據學生較常出錯的問題而進行針對性的訓練,且該知識點又是考試重點內容。該習題設計呈現了層次性、梯度性,能讓全員參與。
四、變式教學策略在廣州中考復習中的實施
初三中考復習時間緊,任務重,教師可將基礎知識和基本技能通過疊合、串聯成典例,通過典例變式訓練讓學生的雙基模塊更鞏固。“重要題目變式練”是數學變式教學學習的重要學習方法與途徑。
(一)變式策略在例習題復習課中的運用
通過變式形成同類的異型,把他們集中在一起,對其題目的立意、解題思路、策略和易錯點等進行歸納總結,使學生形成一個認知體系。下面介紹變式教學的幾種常用方法。
1.方法性變式───“一題多解”
一題多解訓練,能啟發和引導學生從不同角度、不同思路,不同的運算過程去分析解答同一道數學題。切勿因簡單而放棄多角度思考,深刻理解體會解題思路,培養學生的靈活性。
案例一:如圖所示,點E為矩形ABCD的邊AB上一點。將矩形ABCD沿CE對折,點B恰好與AD上的點F重合。
(1)發現不變性:CF=______,EF=_____。
(2)若AB=3,BC=5,求長度:DF=_____,AF=_____。
(3)在(2)的條件下,求BE 的長。
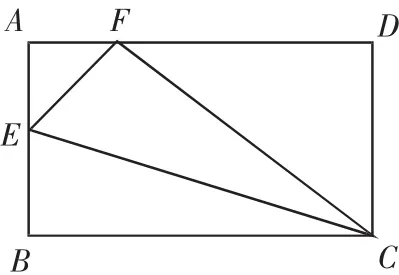
第(3)問解法多種,解法一:利用勾股定理求解;解法二:利用三角形相似求解;解法三:利用等積法求解;解法四:利用三角函數求解。
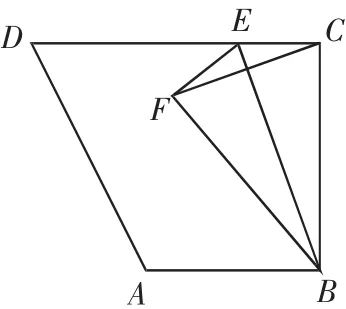
變式:(2014年廣州中考題)如圖,梯形ABCD中,AB∥CD,∠ABC=90°,AB=3,BC=4,CD=5,點 E 為線段 CD 上一動點(不與點C重合),△BCE關于BE的軸對稱圖形為△BFE,連接CF,設CE=x,△BCF的面積為S1,△CEF的面積為S2,當點F落在梯形ABCD的中位線上時,求x的值。
2.強化性變式───“多題歸一”
改變題目的條件或結論等,得到形異質同的一系列問題,歸納出統一的解法,能強化學生對某種特定解法的理解和掌握,使學生觸類旁通。
案例二:勾股定理的應用——折疊問題
1.如圖,在三角形紙片 ABC 中,∠C=90°,∠A=30°,將∠A 沿DE折疊,使點A與點B重合,折痕和AC交于點E,BC=,求EC的長。
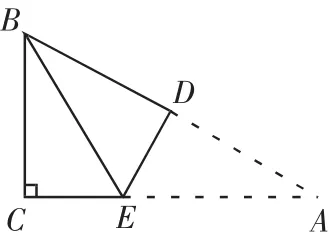
拓展思考:(1)把題目條件“∠A=30°”改為“AC=3”,其他條件不變,則EC的長為______。
(2)若將三角形紙片中∠B沿DE折疊,使點B與點C重合,折痕和AB交于點E(如圖),其他條件不變,則EC的長為___。
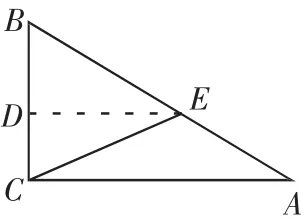
2. 如圖,直角三角形 ABC 中,∠C=90°,AC=6,AB=10,D 為BC上一點,將AC沿AD折疊,使點C落在AB上,求CD的長。
思考(3)如果將△ABC補全為長方形ACBD,線段AB為長方形ACBD的對角線,其他條件不變,請同學們動手畫圖,并思考此時CD的長會變化嗎?
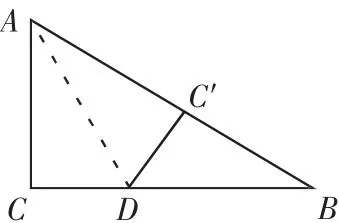
3.如圖,在長方形ABCD中,將△ABC沿AC對折至△AEC位置,CE與AD交于點F。
(1)求證:AF=FC;(2)若 AB=4,BC=8,求 AF 的長以及 S△AFC。
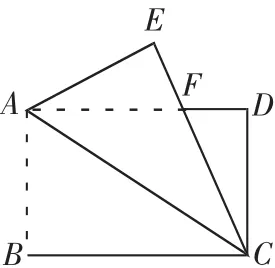
4.如圖,長方形紙片 ABCD 中,AB=4,BC=8,,現將 A、C 重合,使紙片折疊壓平,設折痕為EF,求DF的長,求重疊部分△AEF的面積。
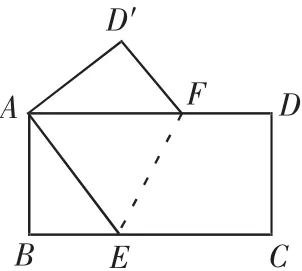
以上習題展現了圖形的折疊有多種情況,可以是點與點,點到線上,點到線外,但折疊的實質是軸對稱(全等性和對稱性),關鍵是通過折疊實現等量轉化(形到數的轉換),利用勾股定理和列方程實現有關線段長度和面積的計算問題。
3.開放性變式───“一題多變”
一題多變是從一道習題出發,通過對習題進行引申或改編,即改變題目條件、結論、題型,或將問題等價替換等手段,使學生掌握與本題相關或相似的一系列數學問題,通過有限的訓練達到掌握多個數學問題的目的。
案例四:已知等腰三角形的腰長是6,底長為8;求周長。
變式1:已知等腰三角形一腰長為5,周長為16,求底邊長。
變式2:已等腰三角形一邊長為4;另一邊長為7,求周長。
變式3:已知等腰三角形的一邊長為7,另一邊長為14,求周長。
變式4:已知等腰三角形的腰長為x,求底邊長y的取值范圍。
變式5:已知等腰三角形的腰長為x,底邊長為y,周長是18。請先寫出x、y的函數關系式,并在平面直角坐標系內畫出它們的圖像。
4.對比性變式───凸顯差異性
直面學生的疑惑,把易混淆的條件、易出錯的知識編制成對比題組,善于做解題后反思、方法歸類、規律小結和技巧揣摩,讓學生理清思維盲區,再進行變式訓練,無疑對學生能力的提高和思維的發展是大有幫助的。
(二)變式策略在專題復習課中的運用
專題復習是第一階段基礎復習的延伸、拓展和深化,用特定的主題進行復習。它特定的主題由復習內容界定,例如函數專題,也可由數學思想方法界定,如數形結合思想專題,或者以考題形式界定。如下表:
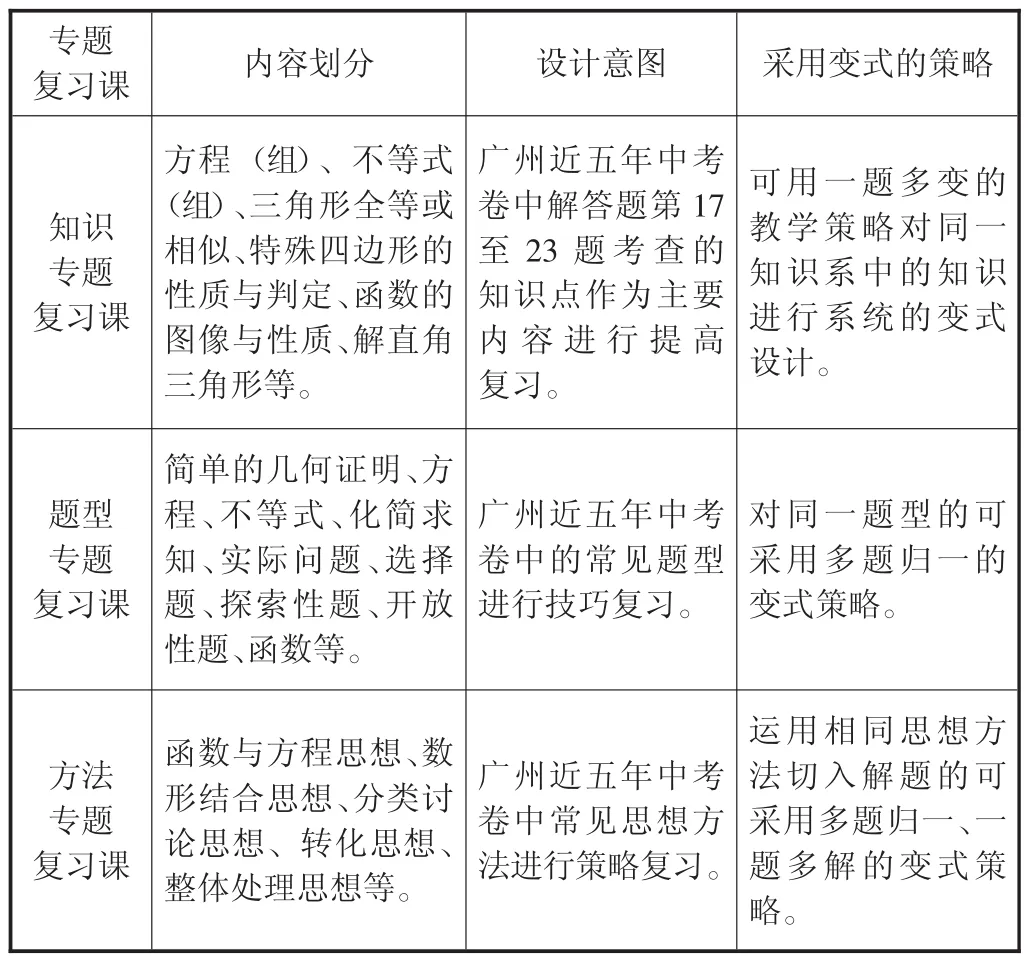
(三)模擬卷講評課中變式策略的運用
第三輪復習是模擬中考的綜合拉練,引導學生解題后反思,查漏補缺,徹底掃除知識結構中的障礙。為此,教師可在模擬卷講評和設計上運用變式策略。
1.在套卷講評中運用變式
試卷講評應針對學生易混淆的知識、易錯點等進行適當的變式、拓展,千萬不能一題一題地講解。可設計關聯性的問題鏈,將一些形異質同或形似質異的試題串聯起來,形成知識網絡,在網絡中獲得新的體驗和啟發。
2.在套卷設計中運用變式
教師要研究歷年中考題,訓練答題技巧,對每套試題的命題原則、題型、考查的知識點都要做到心里有數。有效的訓練對于提高復習的質量有很大幫助。對命題角度好的、能考查重點知識的、綜合性較強的符合中考命題特點的題一定要練熟。
變式教學需要教師對教學過程精心設計,從學生實際出發,不斷完善教學方法,提高教學的實效性。

