不相關并行機節能調度問題建模

孟磊磊 張超勇 詹欣隆 洪 輝 羅 敏

1.華中科技大學數字制造裝備與技術國家重點實驗室，武漢，4300742.湖北汽車工業學院電氣與信息工程學院，十堰，442002

0 引言

據統計，我國擁有機床800多萬臺，每臺機床平均功率按10 kW算，總功率超過8 000萬kW，耗電量是總裝容量為2 250萬kW的三峽電站的3倍多[1]。然而，機床在實際生產中，大部分時間處于空載狀態，據統計，機床大約80%的能量消耗在待機以及關機重啟過程中，真正用于加工的能量占比不足20%[2]，GUTOWSKI等[3]給出的一條汽車自動生產線的能量效率只有14.8%。機床處于空閑等待狀態所消耗的能量為無效能耗，節能調度的主要目的就是減少這部分能耗。

并行機調度問題(parallel machine scheduling problem，PMSP)在實際生產制造過程中比較常見。不相關并行機調度問題(unrelated parallel machine scheduling problem, UPMSP) 是PMSP中最普遍的一類問題, 工件的加工時間取決于所分配的機床，UPMSP已經被證明為NP-hard問題。目前，對UPMSP的研究主要集中在最小化最大完工時間、成本、交貨率等方面[4-6]，而對車間能耗方面不太重視。

當機床連續待機時間較長時，對于允許中途關機的機床可以通過關機/重啟策略來減小機床待機能耗。關機/重啟策略最早由MOUZON等[2]提出，通過對非瓶頸機床實行關機/重啟策略，避免機床長時間處于空閑狀態，可以節約80%的待機能耗。隨后關機/重啟策略逐步被應用于單機[7]、并行機[8-11]調度研究。

針對UPMSP，文獻[12]以加權拖期成本和能耗成本之和為目標，提出了求解該問題的多種啟發式規則方法。文獻[13]研究了并行機批量調度問題，以最小化能耗和最大完工時間為目標，提出了一種基于Pareto的多目標蟻群優化算法。針對加工時間可控的UPMSP，文獻[14]以最小化能耗和最大完工時間為目標，提出了求解該問題的多目標協同果蠅優化算法；文獻[15]同時以最小化加工能耗和最大完工時間為目標，提出了一種高效的多目標memetic差分進化算法。

UPMSP可以通過精確方法，如混合整數規劃(mixed integer programming ,MIP)模型、分支定界等[16]方法求解，也可通過元啟發式方法(如遺傳算法[17]、蟻群算法[8]、分布估計算法[5]等)和啟發式規則[12]等方法求解。精確算法求解速度慢，對于中大規模問題甚至很難求出問題的可行解，但是針對小規模問題，精確算法可以求出調度問題的最優方案，而啟發式方法和元啟發式方法為近似求解方法，雖然在較短時間內可以得出問題的可行解，但解的質量不能保證為最優解。MIP模型是認識調度問題的基礎，是探索與挖掘調度分配規則的關鍵所在[18]。高效的MIP模型可以在相同的時間內得到更好的計算結果，因此構建高效MIP模型具有重要意義。

本文結合UPMSP自身的特點，以節能為目標，考慮關機/重啟策略，提出5個解決該問題的MIP模型，并從建模過程、線性化過程、模型尺寸復雜度以及計算復雜度等方面對5個MIP模型進行對比分析。

1 問題描述

1.1 參數定義

參數定義見表1。其中，為保證每臺機床上都安排工件加工，每臺機床最多可安排n-m+1個工件，每臺機床最大位置數為n-m+1。

1.2 UPMSP描述

UPMSP可描述為:n個工件在m臺機床上加工，每個工件只有一道工序，且同一工件在不同機床上的加工時間是不同的。該問題滿足以下基本假設: 不同工件的釋放時間、交貨期是不同的；所有工件必須在規定的交貨期內完成加工；機床在0時刻處于可用狀態；所有工件在所有機床上的加工時間、加工功率等是已知的；同一機床上不同工件間的轉換時間忽略不計；任一工件可在任一機床上加工；工件一旦開始加工則不可中斷；對于每個機床，在同一時刻最多只能加工一個工件；對于每個工件，在同一時刻最多只能在一臺機床上加工。

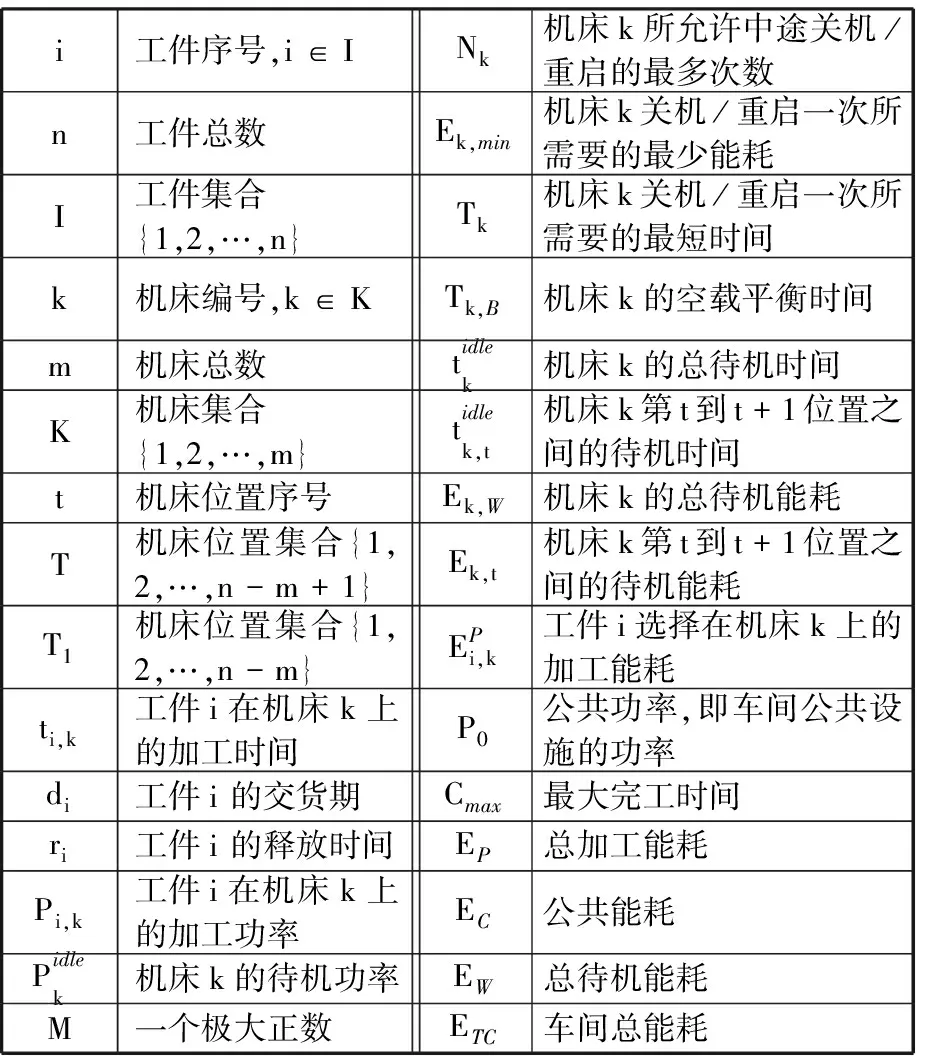
表1 參數定義

UPMSP的目的就是合理地將工件安排在機床上,且確定工件在機床上的加工順序以達到某些調度目標，如最大完工時間、成本、能耗等的最優。本文研究UPMSP節能調度問題，目標為最小化車間總能耗。

1.3 車間能耗分析與建模

車間能耗主要包括機床能耗、公共能耗兩部分，機床能耗進一步可分為加工能耗及待機能耗。

1.3.1加工能耗

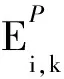
(1)

總加工能耗

(2)

因為每個工件只能選擇在一臺機床上加工，故引入0-1變量Yi,k，如果工件i選擇在機床k上加工，則Yi,k=1，否則，Yi,k=0。

1.3.2待機能耗

待機能耗是指由于上一工件已經加工完，下一個工件還沒有到達，從而使機床出現閑置狀態所消耗的能量，機床k的第t到t+1位置之間的待機能耗

(3)

式中，Fk,t為機床k上第t個位置的結束時間；Sk,t為機床k上第t個位置的開始時間。

機床k的總待機能耗

(4)

所有機床總待機能耗

(5)

1.3.3公共能耗

公共能耗是指車間公共設施的能源消耗，是指為了維持車間正常運行所必須消耗的能源，主要包括照明、通風、供暖、空調等耗能，其值為公共功率P0與最大完工時間Cmax的乘積，可表示為

EC=P0Cmax

(6)

1.3.4車間總能耗

車間總能耗ETC為總加工能耗、待機能耗以及公共能耗之和:

(7)

當機床的一個連續待機時間段Sk,t+1-Fk,t比較長時，可以實施關機/重啟策略，節約無用待機能耗，實現關機/重啟策略的最短待機時間，即空載平衡時間

(8)

空載平衡時間Tk，B表示機床在空載的過程中，當空載的時間不小于一次關機/重啟策略所需要的時間Tk，且機床空載所消耗的能耗不小于機床一次關機/重啟所需要的能耗Ek,min時才可實施關機/重啟策略。

當引入關機/重啟策略后，待機段能耗Ek,t可表示為

(9)

當引入關機/重啟策略后，車間總能耗

(10)

其中，Zk,t為0-1變量，用來控制是否實行關機/重啟策略，當Zk,t=1時，表示在機床k的第t到t+1位置之間實行關機/重啟策略，此時Ek,t為一次關機/重啟所需要的能耗Ek,min；否則,Zk,t=0，Ek,t根據具體待機時間而定。

2 混合整數規劃模型構建

目前關于UPMSP的MIP模型較多, 但是大部分是針對時間目標的[16-17,19]。本文針對UPMSP自身的特點，以節能為目標，同時考慮關機/重啟策略，基于機床位置的Wagner建模思想[20]，建立5個考慮關機/重啟策略的MIP模型，其中2個為基于空閑時間的非線性模型，3個為線性模型(2個線性模型通過將2個非線性模型引入中間決策變量進行線性化處理得到，第3個線性模型基于空閑能耗的建模思想直接構建)。

基于機床位置的Wagner建模方法建立在“機床位置”概念上，即將一個機床按照時間先后分成若干個段，每一段即成為一個位置，一個位置最多只能安排一個工件，因此，只要確定了工件與機床位置的對應關系，工件在機床上的排序即可得到。

5個MIP模型按照建模思路可進一步細分為兩類：第一類是基于空閑時間的建模方法，包括非線性模型1、線性模型1與非線性模型2、線性模型2；第二類是基于空閑能耗的建模方法，包括線性模型3。基于空閑時間的建模方法是指機床待機能耗通過待機段時間與待機功率來計算，而基于空閑能耗的建模方法直接定義空閑段能耗決策變量。

因為基于Wagner建模方法的MIP模型必須引入機床位置占用變量Xi,k,t，Xi,k,t與機床選擇變量Yi,k存在對應關系，因此本文5個模型將不再使用Yi,k，以減少0-1決策變量數，降低模型復雜度。對應關系如下：

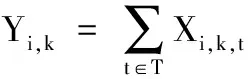
(11)

2.1 模型1

模型1包括非線性模型1以及線性模型1。其中線性模型1通過引入中間決策變量將非線性模型1的目標函數進行線性化處理之后得到。

非線性模型1有Xi,k,t、Zk,t、Sk,t及Cmax4個決策變量，其中，Xi,k,t用于確定工件的機床位置選擇，Zk,t用于確定在機床相應位置是否實行關機/重啟操作，Sk,t和Cmax為連續決策變量。Xi,k,t和Zk,t的表達式分別如下：

為了將非線性目標函數進行線性化處理，引入中間決策變量Ai,k,t、Uk,t和Wk,t，其中Uk,t、Wk,t為連續決策變量，Ai,k,t為0-1中間決策變量，因此線性模型1共有Xi,k,t、Zk,t、Sk,t、Cmax、Ai,k,t、Uk,t和Wk,t7個決策變量。

非線性模型1的目標函數為

(12)

式(12)中，等號右邊第一項表示機床總空閑能耗(待機或關機/重啟)，第二項為機床總加工能耗，第三項為公共能耗。由式(12)可以看出，目標函數是非線性的，存在決策變量相乘的情況，如(1-Zk,t)Sk,t+1、(1-Zk,t)Sk,t以及(1-Zk,t)Xi,k,t，非線性模型求解非常復雜。本文引入中間決策變量Uk,t、Wk,t、Ai,k,t,用Uk,t+1代替(1-Zk,t)Sk,t+1、Wk,t代替(1-Zk,t)Sk,t、Ai,k,t代替(1-Zk,t)Xi,k,t，通過添加相應的約束，實現非線性模型到線性模型的轉換。

線性模型1的目標函數為

(13)

約束條件為

(14)

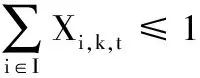
(15)

(16)

ri≤Sk,t+M(1-Xi,k,t) ?t∈T

(17)

(18)

Sk,t≥0 ?t∈T

(19)

(20)

(21)

(22)

(23)

Uk,t+1≥Sk,t+1-MZk,t?t∈T1

(24)

Uk,t+1≤Sk,t+1+MZk,t?t∈T1

(25)

Uk,t+1≤M(1-Zk,t) ?t∈T1

(26)

Uk,t≥0 ?t∈T

(27)

Wk,t≥Sk,t-MZk,t?t∈T1

(28)

Wk,t≤Sk,t+MZk,t?t∈T1

(29)

Wk,t≤M(1-Zk,t) ?t∈T1

(30)

Wk,t≥0 ?t∈T1

(31)

Ai,k,t≤Xi,k,t?t∈T1

(32)

Ai,k,t≤1-Zk,t?t∈T1

(33)

Ai,k,t≥Xi,k,t-Zk,t?t∈T1

(34)

式(14)～式(34)中，?i∈I，?k∈K。式(14)表示任一工件只能選擇在一個機床上加工，且只占用該機床的一個位置；式(15)表示任一機床的任一位置最多只能安排一個工件加工；式(16)表示任一機床的位置按照先后順序安排工件加工；式(17)表示工件只能在到達之后才可以開始加工；式(18)表示工件必須在交貨期內完成加工；式(19)約束決策變量范圍；式(20)表示最大完工時間約束；式(21)、式(22)表示關機/重啟策略約束，約束當機床k的t到t+1位置間存在關機/重啟策略時，即Zk,t=1, 第t+1位置的開始時間與第t位置的開始時間加上該位置的加工時間之差必不小于機床k的空載平衡時間Tk,B,否則，不存在關機/重啟策略；由于平時加工過程中，機床是不允許頻繁關機重啟的(頻繁關機重啟對機床電器元器件壽命影響很大)，因此引入式(23)來限制關機重啟次數; 式(24)～式(27)約束Uk,t+1=(1-Zk,t)Sk,t+1恒成立，其中，成對約束(式(24)與式(25))保證了當機床k的t到t+1位置間不存在關機/重啟策略時，即Zk,t=0時，保證Uk,t+1=(1-Zk,t)Sk,t+1成立；式(26)、式(27)保證了Zk,t=1時，Uk,t+1=(1-Zk,t)Sk,t+1成立，同理，式(28)～式(31)保證了Wk,t=(1-Zk,t)Sk,t恒成立，式(32)～式(34)保證了Ai,k,t=(1-Zk,t)Xi,k,t恒成立。

2.2 模型2

模型2包括非線性模型2和線性模型2。與模型1相比，模型2引入連續決策變量Fk,t，從而減少目標函數中的非線性項、中間決策變量以及相應約束的數量。

非線性模型2的目標函數中含有非線性項(1-Zk,t)(Sk,t+1-Fk,t)，通過引入中間決策變量線性化后即為線性化模型2的目標函數。線性化過程與模型1相似，引入中間決策變量Uk,t、Vk,t，分別代替非線性項(1-Zk,t)Sk,t+1、(1-Zk,t)Fk,t，實現非線性目標函數到線性目標函數的轉換。

模型2中的決策變量為：Xi,k,t、Zk,t、Sk,t、Cmax、Uk,t(含義與模型1中的相同)；機床k上第t個位置的結束時間Fk,t；用來代替非線性項(1-Zk,t)Fk,t的中間決策變量Vk,t。

非線性模型2的目標函數為

(35)

線性模型2的目標函數為

(36)

約束條件為

(37)

Fk,t-M(1-Xi,k,t)≤di?t∈T

(38)

Fk,n-m+1≤Cmax

(39)

Sk,t+1-Fk,t≤Tk,B+MZk,t?t∈T1

(40)

Sk,t+1-Fk,t≥Tk,BZk,t?t∈T1

(41)

Vk,t≥Sk,t-MZk,t?t∈T1

(42)

Vk,t≤Sk,t+MZk,t?t∈T1

(43)

Vk,t≤M(1-Zk,t) ?t∈T1

(44)

Vk,t≥0 ?t∈T1

(45)

其中，?i∈I，?k∈K。式(37)表示機床位置結束時間等于其開始時間加上安排在該位置工件的加工時間；式(38)～式(41)的含義分別與式(18)、式(20)～式(22)約束含義相同；式(42)、式(45)用來約束Vk,t=(1-Zk,t)Fk,t恒成立，其中式(42)～式(43)用來約束當Zk,t=0時，Vk,t=Fk,t=(1-Zk,t)Fk,t成立，式(44)、式(45)用來保證當Zk,t=1時，Vk,t=0=(1-Zk,t)Fk,t成立。

2.3 模型3

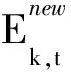
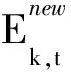
模型3的目標函數為

(46)

約束條件為

(47)

(48)

?k∈K,t∈T1

3 模型對比

模型對比從尺寸復雜度與計算復雜度進行，尺寸復雜度主要包括0-1決策變量數、約束數以及連續決策變量數3個方面。計算復雜度通過規定時間內可求最優解總數Q來判定，包括目標函數值的容差Gap=0最優解個數Q0與Gap≠0最優解個數Q1。當Q相同時，對比Q0；當Q與Q0都相同時，對比Q1；Q、Q0與Q1越大，模型越好。當Q、Q0與Q1都相同時，對比求解時間ttotal，ttotal也是一個重要評價指標，越小越好。Gap可定義為|SC-SB|/|SC|，其中SC表示目前為止可以找到的最優解，SB表示可能的最優解，是當前所有解的下限。可見，Gap值越小越好，當Gap=0時，則得到問題的最優解，程序會自動停止。由此，Gap值也常作為評價MIP模型求解效果的一個指標。

本文所有混合整數線性模型都由商業軟件IBM ILOG CPLEX12.7.1求解，編程語言采用CPLEX Studio自帶OPL語言編寫。CPLEX可以求解線性模型以及非線性模型。模型運行最長時間設置為3 600 s，所有實例獨立運行3次，最終結果取平均值。所有實例在Dell Vostro 3900臺式機上運行，該電腦配置為：Win7系統、i5-4460 3.20GHz四核處理器、8G內存。

如果模型在3 600 s之內自行停止，則可得到最優解且可證明所得到的解為最優解，即Gap=0，如果到截止時間3 600 s，程序強制停止，此時有可能得到Gap≠0最優解，但是Gap≠0，是因為雖然求出了最優解，但是在規定時間內不能證明該解為最優的。本文總共測試10組規模不同的實例。因為目前沒有關于UPMSP能耗相關的對比實例，因此本文隨機生成10組規模不同的實例。

3.1 模型尺寸復雜度對比

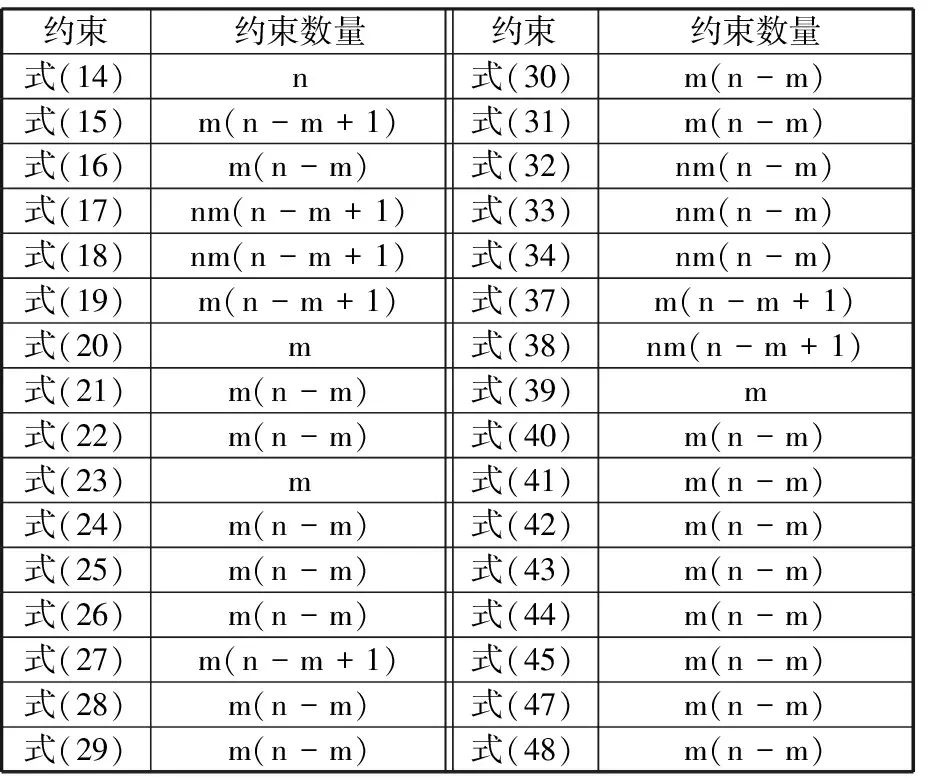
表2 每個約束方程的約束數目

表2給出了上文所列每個約束方程的約束數量，結合每個模型所含約束方程，進而可以得每個模型的約束數(表3)。由各個MIP模型的建模過程可得出每個模型的尺寸復雜度，見表3。模型針對具體實例的尺寸復雜度見表4。其中10*2表示工件數*機床數，其他類推。

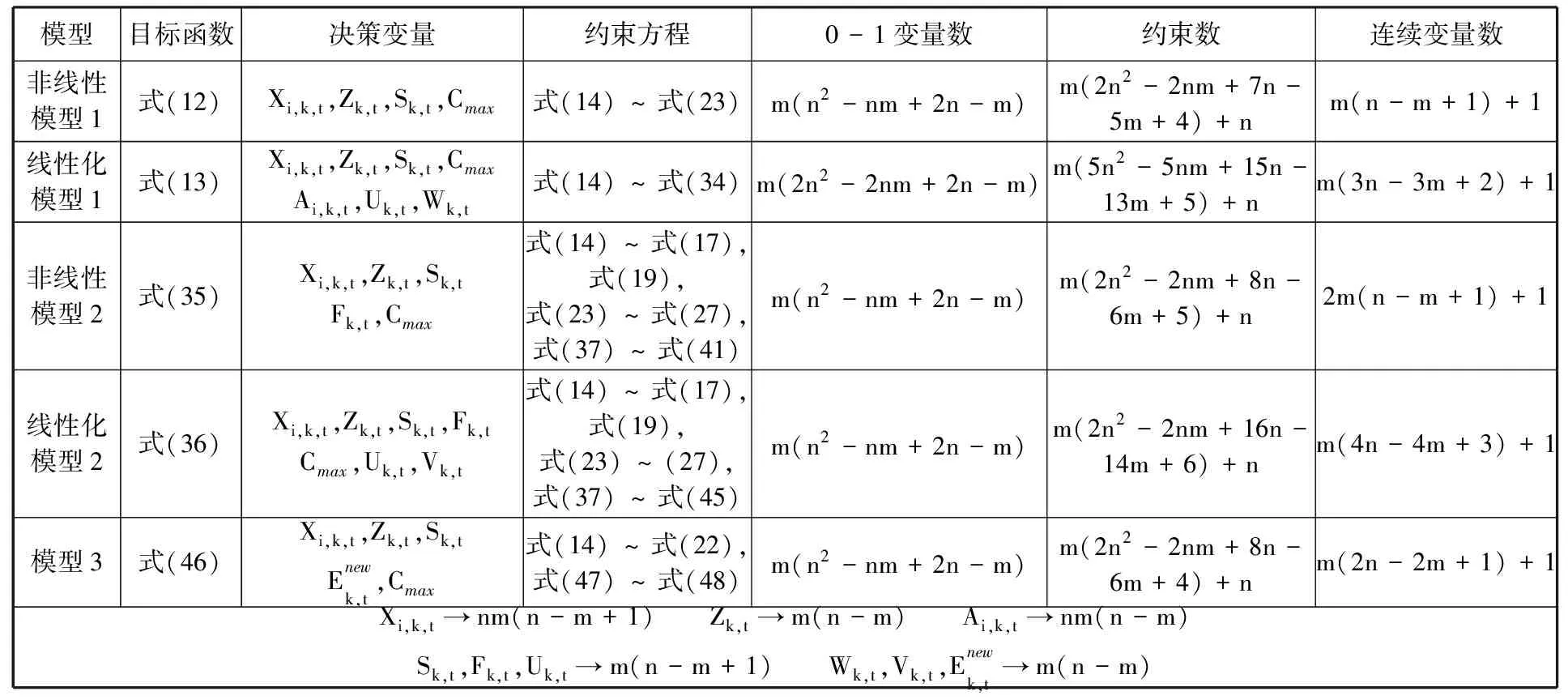
表3 所有模型尺寸復雜度

表4 所有模型針對10組實例的尺寸復雜度

通過表3和表4可知，在0-1決策變量數方面，非線性模型1最多，其他模型相同。這是因為其他模型只含有Xi,k,t、Zk,t兩個0-1決策變量，而模型1除含有Xi,k,t、Zk,t兩個0-1決策變量外，還含有Ai,k,t。

在約束數方面，由表3和表4 可以看出，從多到少依次為線性模型1、線性模型2、非線性模型2、非線性模型1、模型3。這是由于線性模型3基于待機能耗的建模思想，不需要線性化處理目標函數以及相關的約束方程，約束最少。線性模型1需要引入3個中間決策變量(Ai,k,t、Uk,t以及Wk,t)以及相關的約束，而線性模型2只需要引入2個中間決策變量(Uk,t與Vk,t)及相關約束，因此，線性模型1約束數多于線性模型2。非線性模型1與非線性模型2因為沒有引入中間決策變量及相關約束，故約束數分別少于線性模型1與線性模型2。

在連續決策變量數方面，由表3和表4可以看出，連續決策變量數從多到少依次為線性模型2、線性模型1、非線性模型2、模型3、非線性模型1。

3.2 模型計算復雜度對比

決策變量數以及約束數嚴重影響MIP模型的求解效率。對MIP模型影響程度從大到小依次為0-1決策變量數、約束數以及連續決策變量數[21]。除此之外，非線性特征對MIP模型的求解效率影響也很大。

表5 所有模型針對10組實例的求解結果

5種模型針對10組實例的求解結果見表5。其中，SO表示最優解(可通過模型3長時間求解得到)，SC表示當前解(如果在3 600 s內程序自動停止，則為最優解，否則對應3 600 s所能得到的最好解)，帶“*”的解表示此解為可行解但非最優解。

由表5可知，在10個實例中，在規定時間3 600 s內，非線性模型1及線性模型1求解效果最差，只可求出10個實例中的5個，包括3個Gap=0最優解以及2個Gap≠0最優解；線性模型1由于引入3個中間決策變量(Ai,k,t、Uk,t、Wk,t)及相關的約束，決策變量數以及約束數遠多于非線性模型1，這嚴重影響了線性模型1的求解效率，因此求解時間長于非線性模型1。

非線性模型2可以求得10個實例中的7個最優解，其中6個Gap=0 最優解以及1個Gap≠0最優解，效果差于線性模型2(其可求得8個Gap=0 最優解)，且求解時間長于線性模型2，這是由非線性模型2的非線性特征影響的。

非線性模型2和線性模型2由于添加了機床位置結束時間決策變量Fk,t，非線性模型2的非線性項少于非線性模型1，線性模型2的0-1決策變量以及約束數遠少于線性模型1，因此求解效果好于非線性模型1和線性模型1。

模型3基于空閑能耗的建模思想，目標函數是線性的，不需要對其進行線性化處理以及相應的中間決策變量、約束等，從而使模型3具有最少的0-1決策變量、連續決策變量以及較少的約束數，從而模型3求解效果最好。

除此之外，模型的求解效果還依賴具體實例的加工數據，如針對實例20*5，非線性模型2求解時間為224.25 s，線性模型2求解時間為320.00 s，線性模型3求解時間為451.23 s，非線性模型2的求解效果好于線性模型2以及線性模型3，線性模型2效果好于線性模型3。

3.3 節能策略挖掘

實例25*3的具體數據如表6和表7所示。圖1為實例25*3的最優甘特圖。對圖1進行分析，由于考慮了不同工件釋放時間以及交貨期，因此每個工件必須在自身釋放時間-交貨期時間窗內進行加工。工件1～8被分配到機床2上進行加工，機床2在0時刻開機，在212時刻關機。工件10、12、17、18、21、22、25被分配到機床1上進行加工，機床1在230時刻才開機而不是在0時刻開機，從而可以減少待機能耗。工件12在291時刻加工完后，此時下一工件17還沒有到達(其釋放時間為320)，此時機床將處于長時間待機狀態。工件17在363時刻開始加工，在388時刻完成加工，完工時間小于交貨期400。時刻291～363長達72的待機時間將導致機床浪費大量待機能耗，在該待機段內對機床1實行關機/重啟節能策略，可以節約能耗。機床3同樣不是在0時刻開機，而是在199時刻開機以節約能耗，所加工工件依次為9、11、13、14、15、16、19、20、23以及24。由于本文將公共功率設置為20，公共能耗占總能耗比重較大，從而所求能耗最優解中的Cmax也達到了最優(最小)。

表6 實例25*3加工時間數據

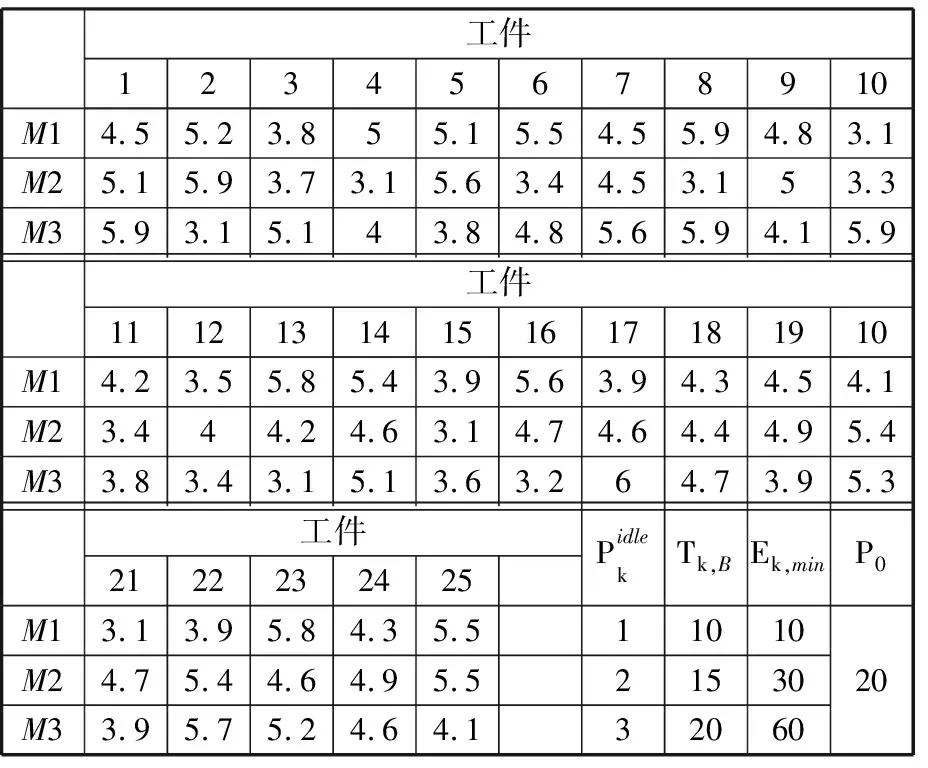
表7 實例25*3加工功率、能耗數據

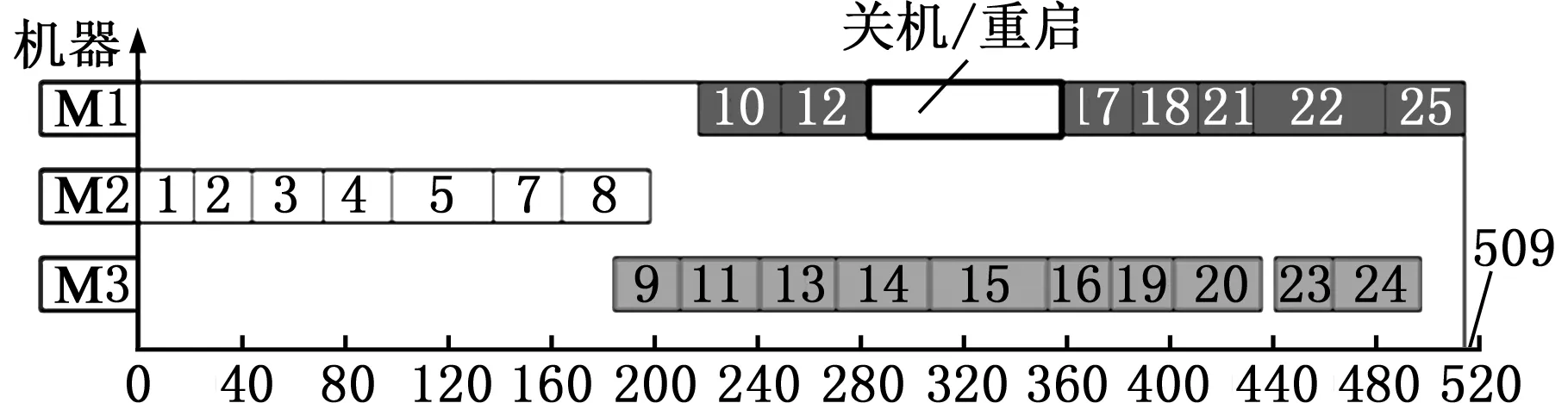
圖1 實例25*3甘特圖Fig.1 Gantt chart of instance 25*3

可見，在保證最大完工時間不變以及滿足交貨期的情況下，通過延遲開機以及關機/重啟策略可以減少機床待機能耗，達到節能的目的。對節能措施的挖掘有利于以后指導元啟發式方法的設計，從而可以有效求解大規模問題。

4 結論

本文以能耗最小為目標，提出了5個考慮關機/重啟策略的不相關并行機MIP模型。試驗結果表明：基于不同建模思路的MIP模型尺寸復雜度、計算復雜度差別很大，基于空閑能耗的線性化MIP模型求解效果最好，在今后的應用過程中應優先選用。

雖然元啟發式方法、啟發式規則等在短時間內可以得到問題較好的解，但是即使是對于小規模問題，也不一定能夠找到最優解，也無法證明所得到的解是最優的，而通過MIP模型求解則可得到并證明最優解。MIP的求解結果可以作為啟發式以及元啟發式等近似方法的參照標準。由于本文直接使用CPLEX對問題進行求解，沒有加入針對問題特性的求解算法等，因此求解效率較低，下一步研究工作將針對本文問題特性，設計相應的求解規則以嵌入到CPLEX，提高求解效率。