基于熵值法徑向基神經網絡的清掃車吸塵口垃圾顆粒駐留時間預測

趙富強 鄧海龍 解璨銘 董 競 李玉貴 王 鐵

1.太原科技大學重型機械教育部工程研究中心，太原，0300242.太原理工大學齒輪研究所，太原，030024

0 引言

隨著城市化進程的提速升級，道路清掃車逐漸成為解決城市道路保潔的有效工具。吸塵口是清掃車吸塵系統的重要部件之一，其結構設計的合理性直接影響清掃車的吸塵效率。垃圾顆粒駐留時間是研究清掃車吸塵口垃圾顆粒運動規律的要素之一,其時間長短將影響清掃車的吸塵效率。預測垃圾顆粒駐留時間能夠為吸塵口結構設計和作業裝置轉速控制提供可靠依據，因此，有必要建立垃圾顆粒駐留時間預測模型。垃圾顆粒駐留時間受路面顆粒的屬性及分布密度、吸塵氣流的分布特性、吸塵口結構等多因素的作用，這些因素之間函數關系不明確。垃圾顆粒駐留時間在這些因素的非線性作用下難以用精確的數學模型進行計算。

目前，清掃車吸塵口結構類、固相類和氣相類因素對吸塵口垃圾顆粒流動的影響成為該領域的研究方向。文獻[1]考慮了出口直徑、出口傾角等結構因素對垃圾顆粒運動的氣相流場的影響；文獻[2]研究了負壓氣流吸拾垃圾顆粒的仿真分析中擴展區域對氣固兩相流的影響；文獻[3]研究了吸塵口前擋板曲率、后擋板傾角等結構因素對入口氣流速度的影響；文獻[4]采用了模糊灰色關聯模型進行研究，并考慮了吸塵負壓、顆粒直徑和環境溫度3個因素對垃圾顆粒駐留時間的影響；文獻[5]考慮了補氣流道、腔體等結構因素對垃圾顆粒運動的影響。上述研究均屬于考慮單類或兩類因素對垃圾顆粒運動特性與駐留時間的研究。

對清掃車吸塵口吸拾性能的求解主要是采用數值模擬和試驗方法。其中，文獻[6]中提出對吸塵口結構的研究采取數值模擬的方法，但需要以網格劃分及網格數量無關性分析為前提，且數值模擬求解耗時長；文獻[4]針對干式環衛吸掃車的吸塵口進行了建模和數值模擬，得到了吸塵口內部流場分布、塵粒的運動軌跡及駐留時間，并進行了優化研究;文獻[7]通過數值模擬方法分析了吸塵口結構參數對吸塵能力的影響，以優化吸塵口結構。上述研究是采用數值模擬的方法，對吸塵口進行氣固兩相流仿真，該方法劃分網格繁瑣、求解困難、仿真速度慢，且對于多因素求解模型，該方法模擬過程復雜，計算過程累計誤差大，精度低。吸塵口性能試驗研究多采用正交試驗的方法，文獻[4]采用正交試驗設計方法對3個因素影響下的清掃車吸嘴結構進行研究;文獻[8]中提出用正交試驗方法來進行多因素、多水平對指標的影響研究；文獻[9]針對旋風分離器多結構參數的變化,以回歸正交試驗法為試驗方案,建立了回歸數學模型，確立了影響分離效率的主要因素;文獻[10]利用正交試驗進行試驗，分析了各因素對氣固兩相流能耗的影響。上述研究中試驗工作量大，集中采樣數據點多，試驗求解只能評價影響因素主次，未能全面考慮影響因素及各種影響因素的取值范圍。

徑向基神經網絡(radial basis function neural network ，RBFNN)具有較好的魯棒性及容錯性等優勢，被廣泛應用到預測、控制等領域[11]。文獻[12]提出了一種基于粒子群優化RBFNN的鋰離子電池健康狀態(SOH)預測方法；文獻[13]提出了一種基于RBFNN的過載加速度的預測方法；文獻[14]提出了一種以RBFNN為模型的多步預測控制方法。此外，文獻[15]提出了一種基于熵的神經網絡模型，采用分配熵無序指數以獲取參數的變化;文獻[16]提出了一種基于熵的人工神經網絡的混合算法，熵單位指數作用于調整多層人工神經網絡模型的輸入。

綜上所述，本文針對多因素作用下垃圾顆粒駐留時間預測難的問題，考慮固相、氣相和結構三類因素，運用拉丁超立方試驗方法[17]獲得試驗樣本，采用基于熵值法的RBFNN預測模型分析上述三類因素對垃圾顆粒駐留時間的影響；在垃圾顆粒駐留時間預測問題中，顆粒直徑、吸塵負壓等因素的變化會對預測結果產生干擾，因此，在輸入數據擾動量中采用熵值法求解的因素權重，以提高預測精度。

1 影響因素分析

1.1 吸塵口結構

本文以清掃車單吸式吸塵口為研究對象，吸塵口由滾刷、殼體、吸塵管、超聲波傳感器、進氣口和出氣口等組成，吸塵負壓可調，如圖1a所示。吸塵口工作原理如圖1b所示，路面垃圾顆粒在滾刷作用下由進氣口運動到殼體內，吸塵管連接風機，吸塵口內的垃圾顆粒在負壓氣流的作用下，從出氣口吸出。在工作過程中，吸塵口吸拾垃圾顆粒的性能直接影響清掃車的吸塵效率。

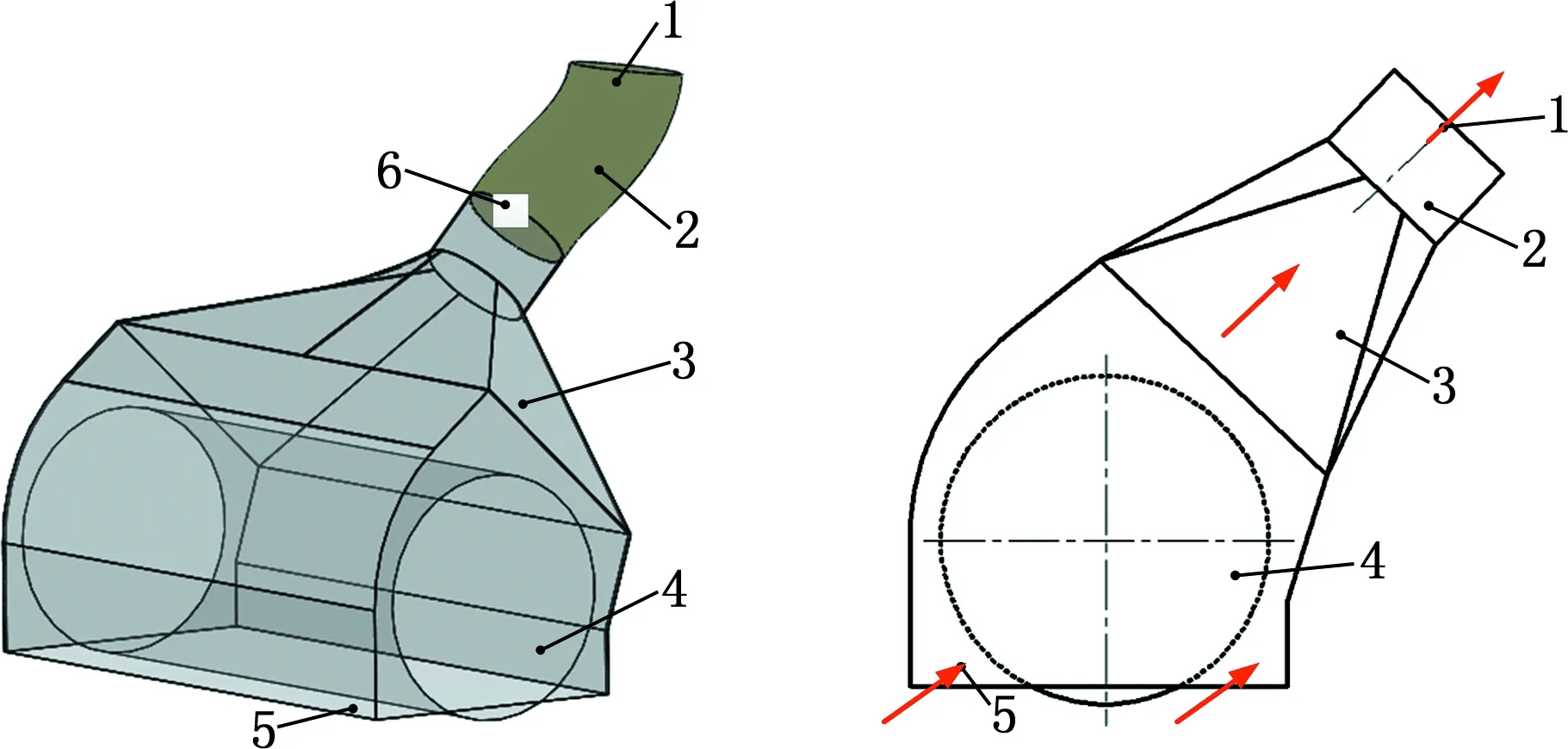
1.出氣口 2.吸塵管 3.殼體 4.滾刷 5.進氣口 6.超聲波傳感器 (a)吸塵口模型 (b)工作示意圖圖1 單吸式吸塵口結構Fig.1 Structure of the single suction port

1.2 垃圾顆粒駐留時間的多因素預測模型

影響垃圾顆粒駐留時間的因素按作用機理分為固相、氣相和結構三類。其中，固相類因素取決于垃圾顆粒的屬性及分布特性；氣相類因素受到吸塵裝置工作參數的影響，吸塵負壓對腔體內壓力和速度分布有決定性作用，滾刷轉速間接作用于腔體內的流場，且兩者共同作用時，與流場速度之間成非線性關系[18]；結構類因素取決于吸塵口的結構參數，影響能量損耗、流場分布。

基于以上影響參數，建立垃圾顆粒駐留時間T關于空間位置(x,y,z)的多因素模型：

T(x,y,z)=T(X1，X2，X3)

(1)

X1=(x11,x12,x13)T

X2=(x21,x22,x23)T

X3=(x31)T

式中，T為垃圾顆粒駐留時間;X1為固相類因素;x11為顆粒密度；x12為顆粒直徑；x13為顆粒流量；X2為氣相類因素；x21為吸塵負壓；x22為滾刷轉速；x23為環境溫度；X3為結構類因素；x31為吸塵管直徑。

垃圾顆粒駐留時間T是由不同影響因素條件下的仿真模擬值或試驗測試值組成的訓練樣本集，通過本文提出的基于熵值法的RBFNN算法，求得給定影響因素下的預測值。

2 基于熵值法的RBFNN算法

熵值法可用來判斷指標的離散程度，離散程度越大，對指標綜合評價的影響越大。同時，RBFNN具有最佳逼近性能和全局最優特性，能通過大量離散點逼近未知的非線性函數，可實現對垃圾顆粒駐留時間模型的預測，因此，本文提出基于熵值法的RBFNN預測方法來分析三類因素共同作用下的垃圾顆粒駐留時間。

2.1 熵值法求解多因素權重[19]

為了分析各因素變化對垃圾顆粒駐留時間的影響，采用熵值法求解n個試驗點對應的因素權重，具體步驟如下。

(1)計算每個試驗點中單個因素占全部試驗點中該因素的比重：

(2)

式中，zij為第i個試驗點的第j項因素的影響程度。

(2)分析第j項因素的熵值：

(3)

(3)計算信息熵冗余度：

gj=1-ej

(4)

(4)計算各因素的權重：

(5)

2.2 添加權重擾動的RBFNN算法

對試驗點矩陣添加擾動，建立基于熵值法的RBFNN預測模型。RBFNN模型表示為(m-g-1)，其中，各因素作為輸入層，輸入層的節點為m個；隱含層的節點為g個；垃圾顆粒駐留時間為輸出層，輸出層的節點數為1。

定義由n個試驗點組成試驗點矩陣Yn×m；在n個試驗點中選l個試驗點組成矩陣Yl×m，將該矩陣作為訓練神經網絡模型的輸入值，對應的垃圾顆粒駐留時間試驗值ti作為輸出值。剩余的h(h=n-l)個試驗點組成矩陣Yh×m，將該矩陣作為預測模型的輸入值，對應的垃圾顆粒駐留時間預測值ui作為輸出值，得到RBFNN模型的輸出誤差：

(6)

式中，h為預測試驗點個數。

調整神經網絡模型的預測精度的步驟如下。

(1)由式(5)求得影響吸拾性能的多因素初始權重后，對l個試驗點組成的矩陣Yl×m添加擾動，生成擾動試驗點矩陣：

(7)

P=(1,1,…,1)T

V′=V+α

(8)

α=(α1,α2,…,αm)

V=[V1V2…Vm]

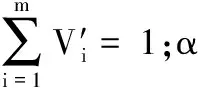
(9)

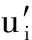
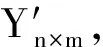
(10)

式中，r為離差設定值。

通過尋找擾動試驗點和原試驗點的離差極小值，以保證此算法的可靠性；利用模型輸出誤差保證基于熵值法的RBFNN模型的預測精度。

3 吸塵口試驗分析

3.1 影響垃圾顆粒駐留時間的因素分析

影響垃圾顆粒駐留時間的3類因素及取值范圍見表1，其中，固相類因素個數a取3，氣相類因素個數b取2，結構類因素個數p取1。

表1 因素類型及范圍

根據太原市道路垃圾直徑、類型及分布密度選擇顆粒直徑、顆粒密度及顆粒流量[20]；根據清掃速度在3～20 m/s的中型清掃車的滾刷轉速及風機風壓選擇滾刷轉速和吸塵負壓；結構類因素選擇吸塵管直徑，吸塵管直徑取值范圍依據吸塵腔內的壓力損失及平均氣流速度來確定[21]。依據上述因素類型及范圍設計吸塵口試驗，并獲取試驗點矩陣Yn×m，分別以仿真試驗[22]和測試試驗兩種方法求解垃圾顆粒駐留時間ti(i=1,2,…，n)。

3.2 吸塵口仿真模擬試驗分析

仿真模擬試驗采用拉丁超立方試驗方法，設計包含6個影響因素的100個試驗點。采樣空間分為3層，每層橫/縱坐標各代表1個影響因素；將各影響因素的取值范圍等分成100個區間，則每層可得到100×100個子域；再在各子域中隨機抽取1個點，將這些點取整組成一組向量作為影響因素的樣本；將樣本代入吸塵口仿真模型中得到氣相流場特性和垃圾顆粒運動軌跡。

以其中1個試驗點仿真結果為例進行分析，該試驗點的輸入影響因素如下：顆粒直徑d為1 mm，顆粒密度ρ為1 200 kg/m3，顆粒流量q為50 g/s，滾刷轉速nr為450 r/min，吸塵負壓ps為3.5 kPa，吸塵管直徑D為110 mm。

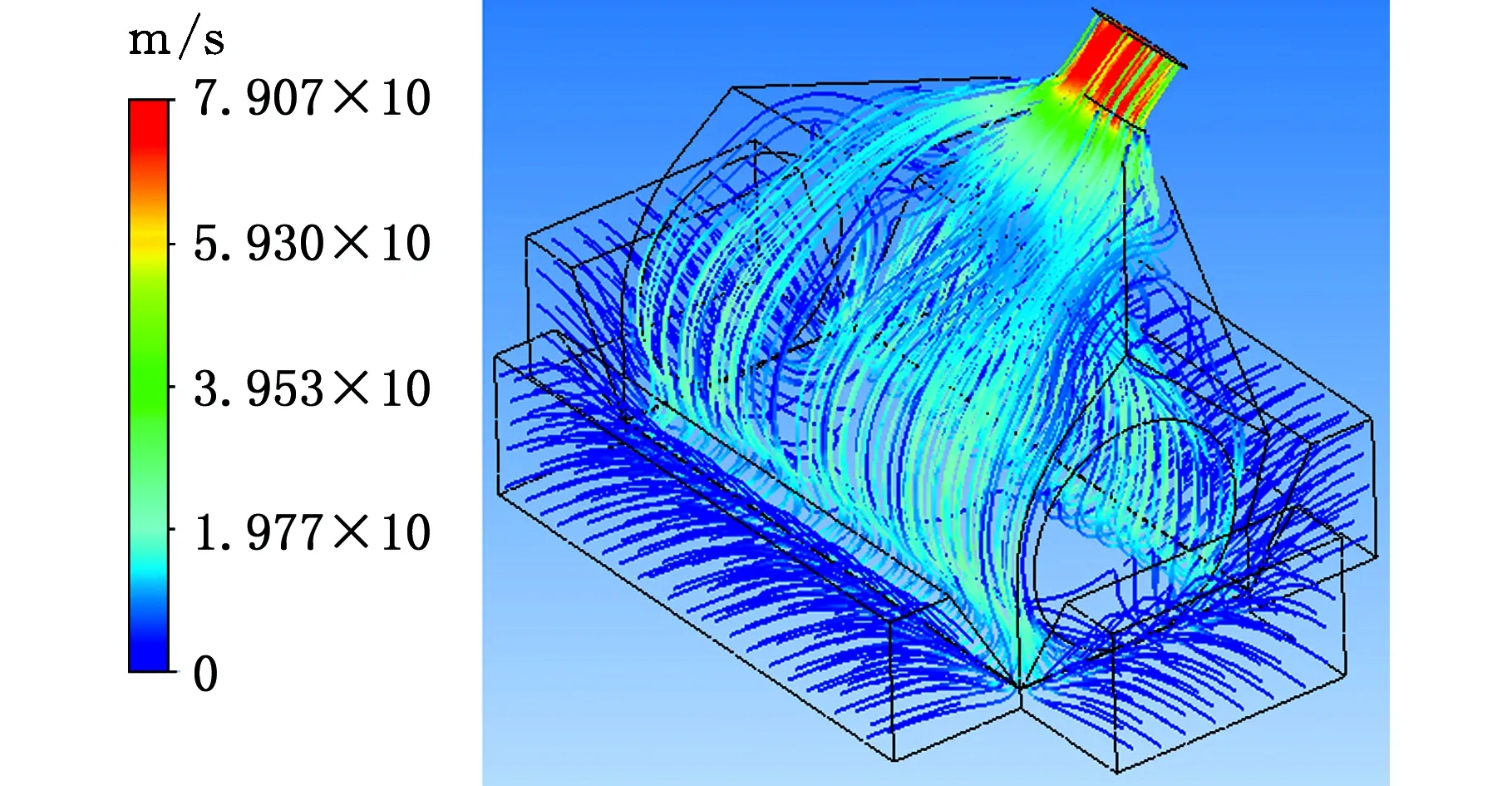
圖2 吸塵腔體內的氣體流線Fig.2 Gas flow in the suction chamber

吸塵腔內的氣體流線仿真結果見圖2。外界氣體受到腔內負壓的作用，從吸塵口底部進入，繞過滾刷的氣流由吸塵腔到達吸塵管。由于吸塵腔兩側氣流向上的運動被殼體限制，氣流向中間運動，與繞過滾刷的其他氣流相撞，因此，在滾刷兩側上部位置產生渦流。由圖2可以看出，吸塵管附近的平均氣流速度為35 m/s，達到了吸拾垃圾顆粒的最小速度，因此吸塵腔內的垃圾顆粒在氣流的帶動下從吸塵管排出。

垃圾顆粒在吸塵腔內的運動軌跡見圖3，可以看出，垃圾顆粒通過滾刷刷毛獲得初速度后，兩側的垃圾顆粒受到腔體內渦流的作用與腔體發生多次碰撞，而中間的垃圾顆粒在速度較高氣流的作用下直接由吸塵管排出。由圖3可知顆粒不同時刻在腔體內的位置，從而可大致判斷顆粒在吸塵口中的駐留時間。

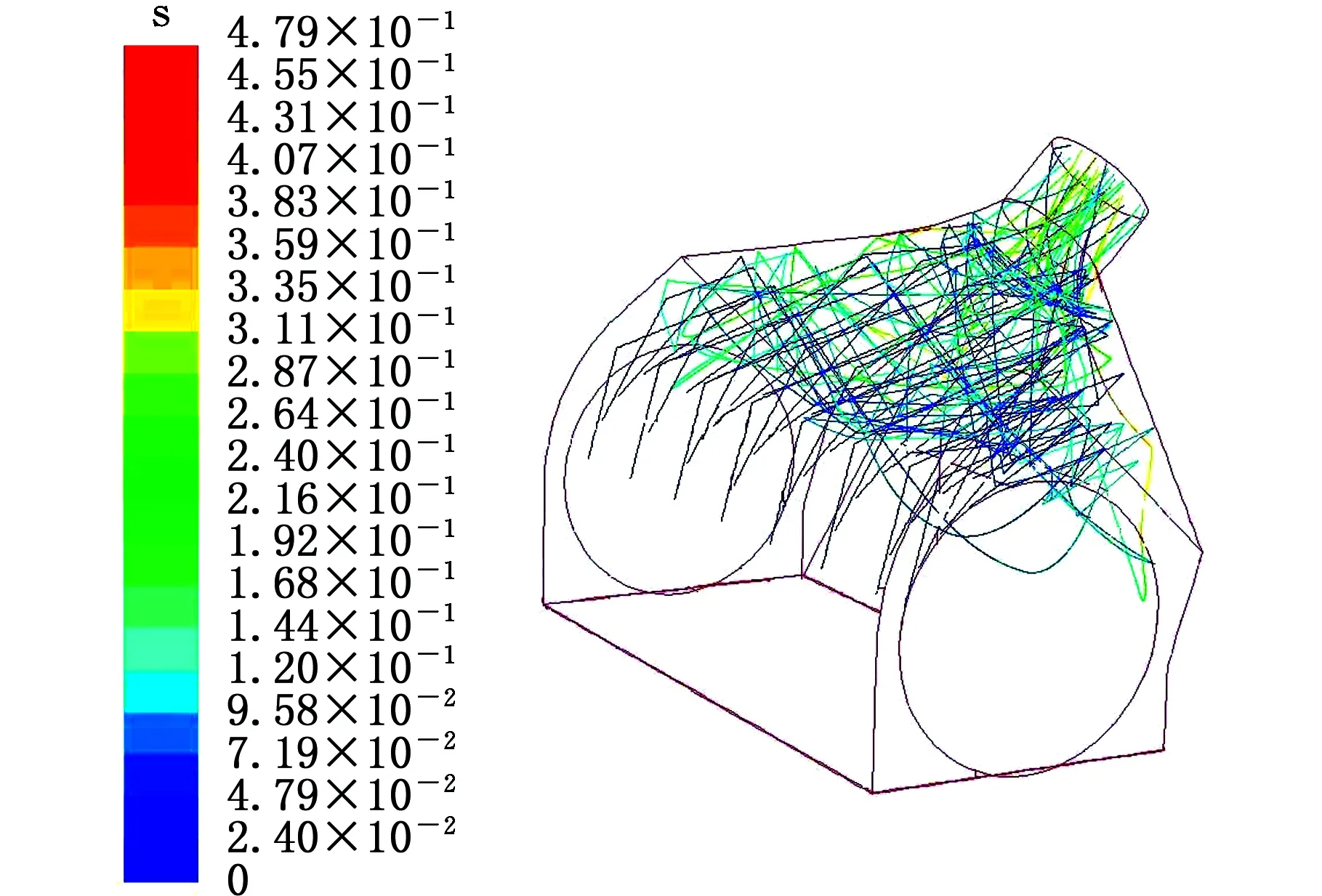
圖3 垃圾顆粒運動軌跡Fig.3 Trajectory of waste particles

采用熵值法的RBFNN算法對仿真試驗結構預測分析的具體迭代過程如下。

(1)將100個試驗點組成矩陣Y100×6，選取其中80個試驗點組成矩陣Y80×6，其余20個試驗點組成矩陣Y20×6。將矩陣Y80×6作為訓練神經網絡模型的輸入值，垃圾顆粒駐留時間試驗值ti作為輸出值；將矩陣Y20×6作為預測模型的輸入值，垃圾顆粒駐留時間預測值ui作為輸出值。

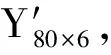
(4)將矩陣Y20×6及對應的垃圾顆粒駐留時間ui作為RBFNN模型的預測值，依據迭代終止條件(式(9))，判斷模型精度是否滿足條件，若不滿足，則返回步驟(2)；若滿足，則可執行下一步。

3.3 吸塵口測試試驗分析

在自主研發的清掃車吸拾性能試驗臺上進行了吸塵口垃圾顆粒駐留時間的測試試驗，如圖4所示。該試驗臺能模擬清掃車吸塵裝置工作，吸塵電機額定功率為4.0 kW，風機全壓為7 kPa，滾刷電機功率為0.6 kW，滾刷額定轉速為900 r/min。采用滾刷電機控制器調節滾刷電機轉速，以使滾刷轉速與仿真邊界條件中的滾刷轉速保持一致。采用吸塵電機控制器調節吸塵電機轉速，以使吸塵管的吸塵負壓與仿真邊界條件中的吸塵負壓保持一致。

(a)整體結構 (b)吸塵口圖4 清掃車吸拾性能試驗臺Fig.4 Test platform of sweeper pick up performance

數據采集系統由安裝在進氣口、吸塵腔、出氣口、風機進口和風機出口位置的差壓變送器，安裝出氣口位置的超聲波傳感器，安裝在滾刷的激光測距傳感器和安裝在電機支架上的磁電式轉速傳感器組成，各傳感器的型號及參數見表2。差壓變送器用于采集吸塵裝置的風壓信號，磁電式轉速傳感器用于采集吸塵電機和滾刷電機的轉速。

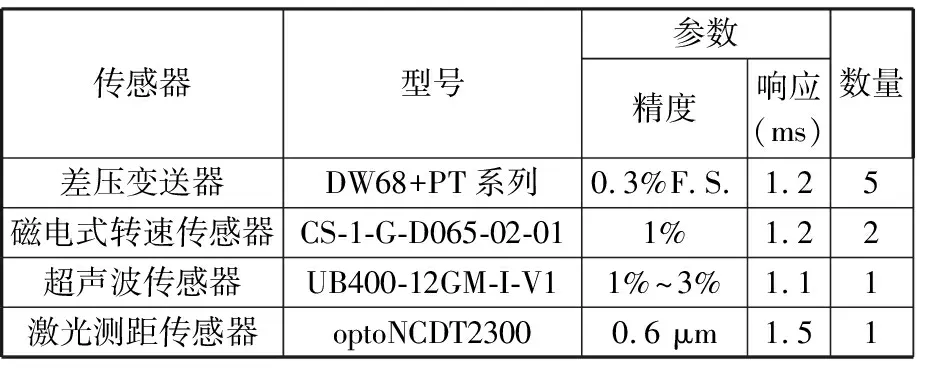
表2 傳感器型號及參數

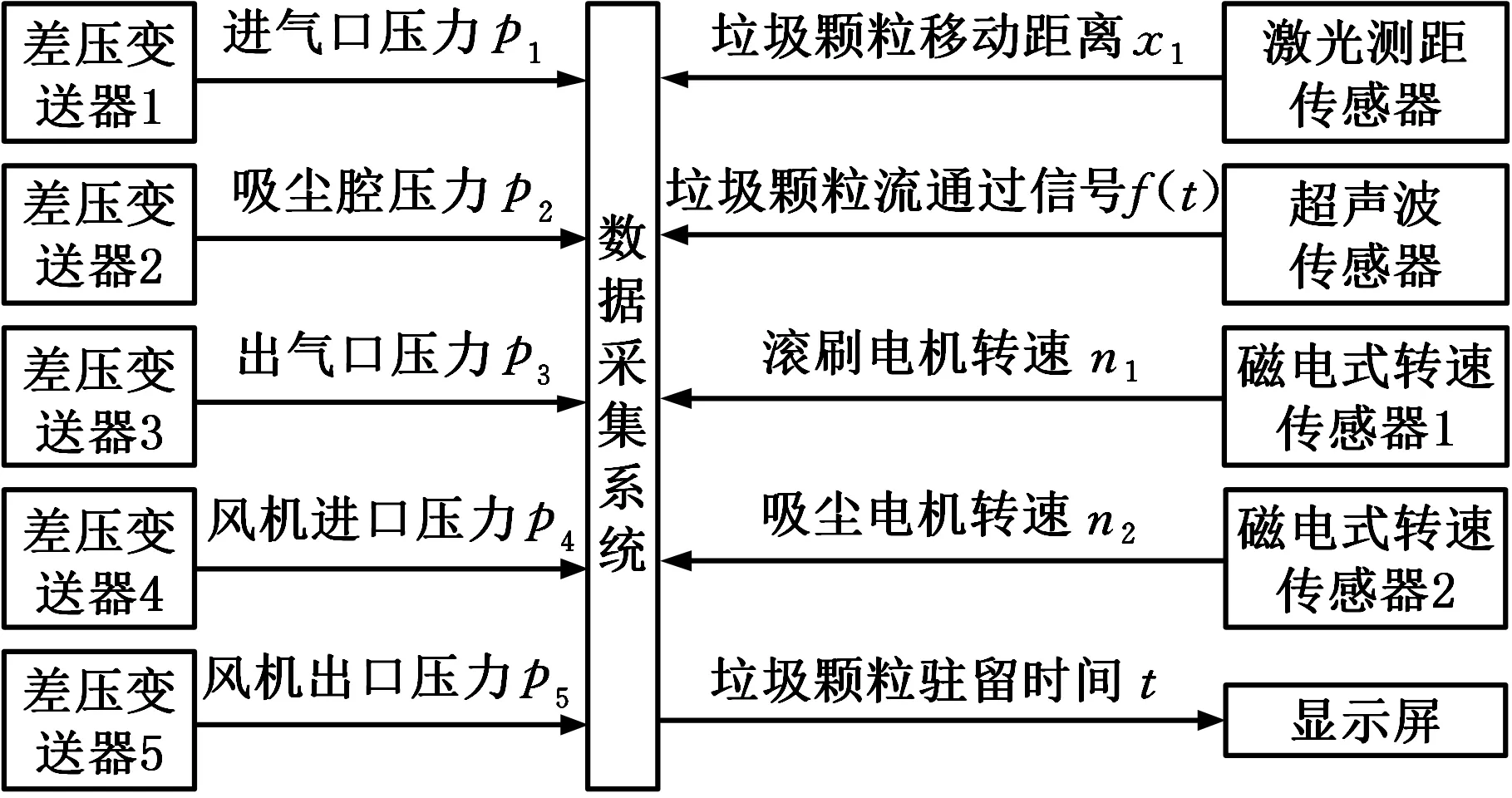
圖5 數據采集系統Fig.5 Data acquisition system

數據采集系統接收激光測距傳感器、超聲波傳感器等采集的信號，并輸出垃圾顆粒駐留時間，如圖5所示。將激光測距傳感器測得垃圾顆粒到達滾刷前側的時刻作為起始時刻，將超聲波傳感器測得垃圾顆粒流全部通過出氣口的時刻作為終止時刻。

測試時，根據各試驗點的6個因素值設置試驗狀態，為了減小試驗誤差，對各試驗點重復測試3次，將所測得的時間取平均值作為測試值，再依次測試得到其余試驗點對應的垃圾顆粒駐留時間。

4 結果分析

由吸塵口測試試驗得到全部試驗點的垃圾顆粒駐留時間后，選取吸塵口測試試驗中前80個試驗點作為RBFNN預測模型訓練樣本，剩余20個的試驗點作為預測樣本。將預測樣本所對應的仿真值和測試值進行比較，見圖6，可以看出，仿真值與測試值的變化趨勢一致，且測試值略大于仿真值，其原因是仿真時不考慮吸塵口漏風等壓力損失，導致垃圾顆粒駐留時間偏小。

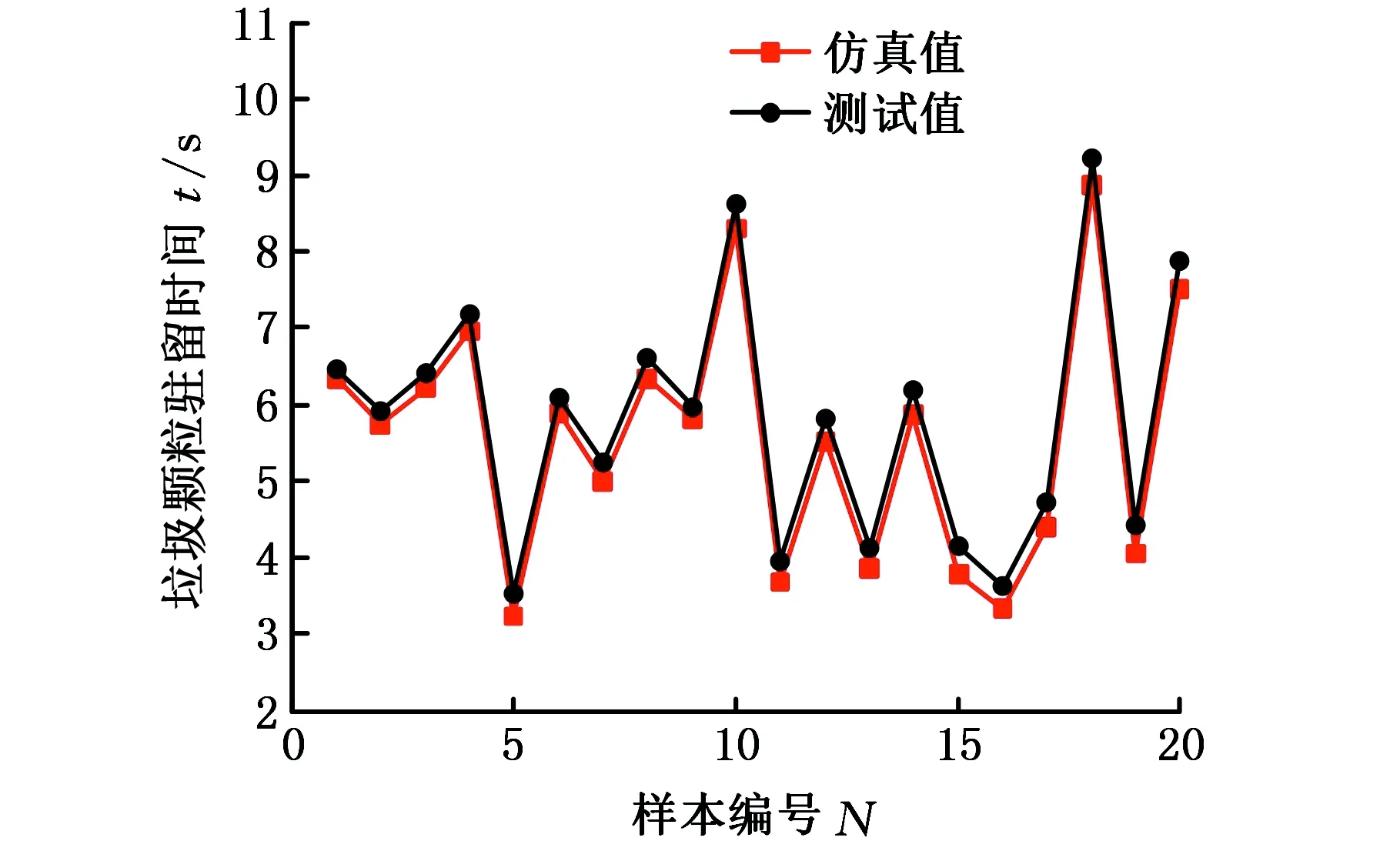
圖6 垃圾顆粒駐留時間測試值和仿真值Fig.6 Experiment and simulation values of the residence time of waste particles

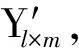
圖7 垃圾顆粒駐留時間測試值和預測值Fig.7 Experiment and prediction value of the residence time of waste particles

將基于熵值法的RBFNN預測模型和傳統RBFNN預測模型的預測值與測試值進行比較，見圖7，可以看出，基于熵值法的RBFNN預測值、傳統RBFNN算法的預測值和試驗測試值的變化趨勢一致。對比測試值與預測值可知(表3)，采用傳統RBFNN算法的平均誤差0.54 s明顯大于采用基于熵值法的RBFNN算法的平均誤差0.23 s，此外，采用傳統RBFNN算法的最大誤差1.02 s也大于采用基于熵值法的RBFNN算法的最大誤差0.51 s。由此可知，基于熵值法的RBFNN的預測模型具有較高的預測精度。

表3 測試值與預測值對比

5 結論

(1)本文提出了一種基于熵值法RBFNN的垃圾顆粒駐留時間預測方法，該方法考慮了顆粒直徑、顆粒密度、顆粒流量、滾刷轉速、吸塵負壓、吸塵管直徑等6個因素，并對試驗點進行了垃圾顆粒駐留時間的仿真模擬和試驗測試。

(2)與傳統RBFNN算法對比可知，采用基于熵值法的RBFNN算法進行吸塵口垃圾顆粒駐留時間預測，其預測值的平均誤差與最大誤差均小于傳統RBFNN算法預測值的平均誤差與最大誤差，因此所提方法具有求解精度高的優點。

(3)所提方法有助于解決吸塵口垃圾顆粒駐留時間預測不準確的問題，為提高清掃車吸塵口優化設計提供參考。