大尺度模擬二維晶粒長大過程的相場法研究

梁冬梅，李 潔，張義靈，羅志榮

（玉林師范學院 物理科學與工程技術學院，廣西 玉林 537000）

0 前言

多晶材料中晶粒長大過程控制著微觀組織結構的演變，而晶粒組織結構直接影響著材料性能[1]，研究多晶材料晶粒長大過程中晶粒尺寸、邊數的變化以及單個晶粒長大動力學具有重要意義。

傳統上對晶粒長大的研究主要集中在理論和實驗兩方面[2]。隨著科學技術與計算機技術的快速發展，出現了許多計算機模擬晶粒長大的方法，如蒙特卡羅（MC）[3-5]、元胞自動機（CA）[6]和相場（PF）[7]等方法。孫亞等人[8]采用相場法對二維晶粒長大過程進行仿真，研究了晶粒尺寸分布與拓撲演變；花福安等人[9]結合晶粒長大速率的統計理論，采用CA方法對基于曲率驅動機制的晶粒長大過程進行了研究；羅志榮等人[10]采用相場法探討了不同初始微結構（柱狀和梯度）對晶粒長大過程及其長大動力學的影響；Z?llner和Rios[11]采用MC方法模擬了二維晶粒長大過程中3種經典拓撲轉變以及單個晶粒長大軌跡。上述研究采用了不同的方法模擬晶粒長大過程，但其模擬尺度均較小。實際上，模擬尺度越大，數據離散程度越小，獲得的晶粒長大動力學和尺寸分布越準確[12]。然而，目前大尺度模擬二維晶粒長大過程中的晶粒半徑和邊數分布以及單個晶粒長大動力學的相場法研究還鮮有報道。相場法在模擬晶粒長大過程中對晶界做彌散化處理，不必直接跟蹤動態界面，且易于將物理場等因素對晶粒長大的影響考慮進來，物理意義更明確[2]。故本研究采用相場法大尺度模擬二維晶粒長大過程，從動力學角度研究晶粒長大的特征并定量分析晶粒長大過程中相對晶粒半徑、晶粒邊數的分布特點，揭示二維晶粒長大的規律。

1 理論模型

1.1 相場模型

在相場模型中，用場變量ηi（r，t）（i=1，2，…，p）表示多晶材料內不同晶粒的取向，其中p是晶粒取向個數，ηi（r，t）是空間位置r和時間t的連續函數。在任意晶粒內部，其場變量的絕對值，其余場變量 ηj≠i=0；在晶界處，在0～1之間連續變化，形成彌散界面。系統總自由能函數F由場變量及其梯度項表示為[13]

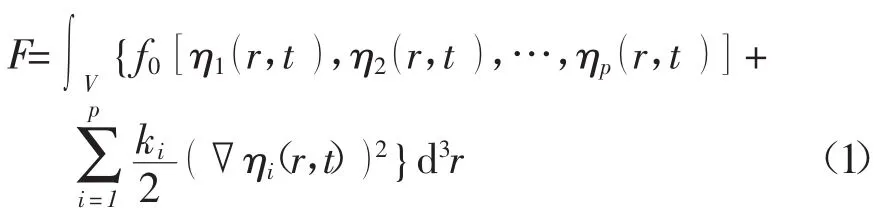
式中 ki為梯度能系數，與界面能有關；f0為局部自由能密度函數，表示為[13]：

式中 α、β和γ為正實數，γ＞β/2。

由于取向場變量為非保守場變量，根據Ginzburg-Landau（弛豫）方程可得取向場變量在空間與時間上的演化公式為[13]：

式中 Li為弛豫系數，與晶界遷移率有關。

在時間上，對動力學方程式（3）使用顯式Euler迭代公式可得[13]

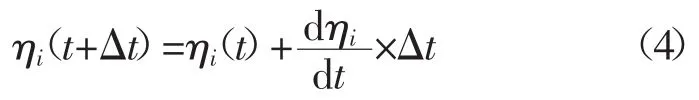
式中 Δt為離散時間步。另外，在空間上，對取向場變量的Lapace算子操作處理到次近鄰格點[13]

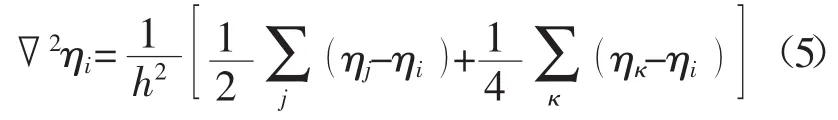
式中 h為空間步長；j與κ分別為i的最近鄰和次近鄰格點。

1.2 參數設置

本研究模擬二維正常晶粒長大過程，界面能和晶界遷移率均為各向同性。仿真時將連續區域離散為四方格點，選取4 096×4 096的二維矩陣，采用周期性邊界條件。場變量的初值取[-0.001，0.001]之間的隨機數，晶粒取向個數p=36。其他參量設置為α=β=γ=1.0，ki=2.0（界面能各向同性），Li=1.0（晶界遷移率各向同性），Δt=0.25，h=2.0。計算過程中對系統所有格點嘗試1遍后計為1個模擬時間步（ts），最終模擬出整個晶粒的長大過程。

2 模擬結果與分析

2.1 晶粒半徑與邊數分布規律

在晶粒長大過程中，系統晶粒個數由71 140個（t=1 000 ts）逐漸減少至 10 276個（t=10 000 ts）。統計這些晶粒，得到不同演化時間的相對晶粒半徑分布曲線，如圖1所示。由圖1可知，隨著時間的增加，相對晶粒半徑分布的最大頻率始終在R/Rc=1附近；而 R/Rc＜0.2，R/Rc＞2 出現的頻率較低，即半徑偏大或偏小的晶粒較少，且沒有出現異常大（R/Rc＞2.5）的晶粒。說明系統中晶粒半徑分布均勻，晶粒長大符合正常晶粒長大規律。還可以看出，不同演化時間的相對晶粒半徑分布曲線相似度較高，說明相對晶粒半徑分布具有自相似性，這與采用相同方法模擬得到的結果[8]相比，本研究大尺度統計得到的相對晶粒半徑分布較穩定，結果更加精確。

不同演化時間的晶粒邊數分布曲線如圖2所示。由圖2可知，系統中五邊形晶粒出現頻率最高，六邊形晶粒僅次之，邊數小于3和大于9的晶粒出現頻率較低，晶粒邊數絕大部分分布在4～8之間。不同演化時間的晶粒邊數分布曲線非常相似，分布頻率相對穩定，說明晶粒邊數分布具有時間不變性（自相似性），與采用CA方法模擬的結果[14]一致。

不同演化時間的晶粒邊數與晶粒半徑的關系曲線如圖3所示。晶粒半徑表示所有邊數相同的晶粒半徑的平均值。由圖3可知，晶粒邊數與晶粒半徑呈正相關，在同一演化時間，晶粒邊數越大，晶粒半徑越大；隨著演化時間的增加，晶粒半徑也隨之增大，且演化時間越長，晶粒半徑隨邊數增加得越快。

圖1 不同演化時間的相對晶粒半徑分布

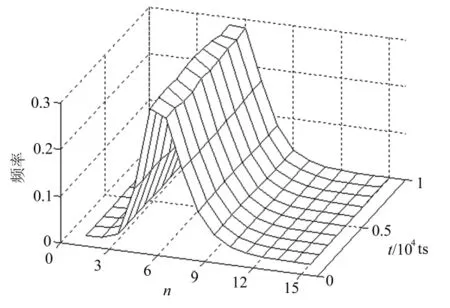
圖2 不同演化時間的晶粒邊數分布

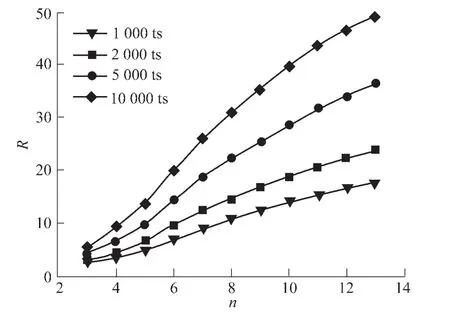
圖3 不同演化時間的晶粒邊數與晶粒半徑的關系

2.2 單個晶粒長大動力學

晶粒長大是大晶粒不斷吞噬近鄰小晶粒的過程。為了探究晶粒長大規律，有必要對單個晶粒的半徑與邊數進行研究，Hillert提出單個晶粒長大速率的理論方程為[15]

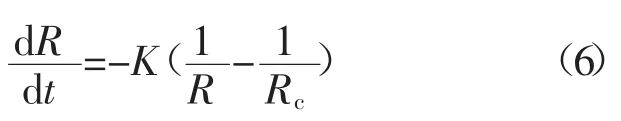
式中 K為一個正常數；R為單個晶粒的半徑；Rc為臨界晶粒半徑（二維網格下系統的平均晶粒半徑）。根據式（6）在二維網格下晶粒半徑大于臨界半徑的晶粒（大晶粒）趨于長大，反之亦然。本研究對dR/dt的計算使用有限差分近似[16]

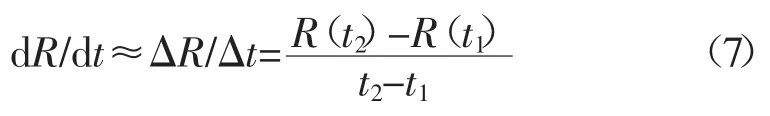
式中 t1和t2分別為 2 000 ts和2 010 ts，Δt=10 ts。統計2 010 ts時系統中41 845個晶粒的增長率與半徑、邊數的關系，結果如圖4和圖5所示。

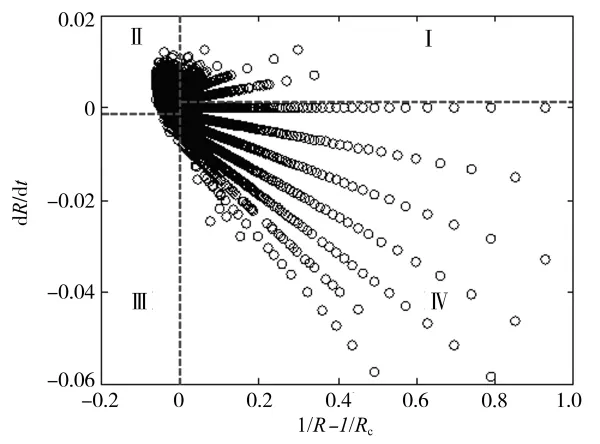
圖4 晶粒增長率與晶粒半徑的關系

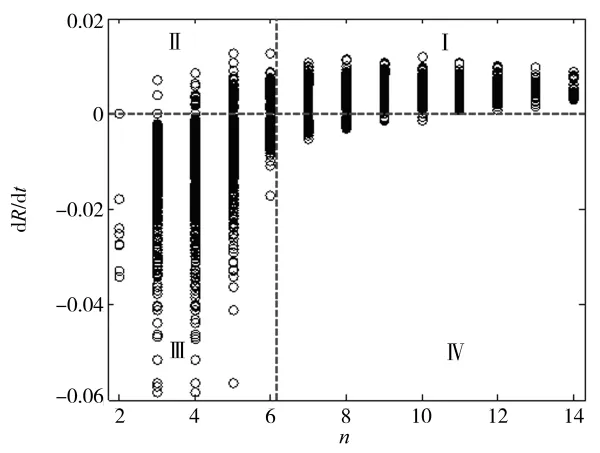
圖5 晶粒增長率與晶粒邊數的關系

晶粒增長率與半徑的關系如圖4所示。圖4可分為 4 個區域，分別是Ⅰ區域（1/R-1/Rc＞0，dR/dt＞0）、Ⅱ區域（1/R-1/Rc≤0，dR/dt≥0）、Ⅲ區域（1/R-1/Rc＜0，dR/dt＜0）和Ⅳ區域（1/R-1/Rc≥0，dR/dt≤0），各區域分布頻率分別是7.58%、34.21%、4.37%和53.84%。由圖可知，系統中小晶粒居多且絕大部分小晶粒趨于縮小，絕大部分大晶粒趨于長大；在1/R-1/Rc=0附近晶粒分布密度最高，增長率趨于0，晶粒變化不明顯；半徑接近臨界半徑的晶粒，增長率越慢；晶粒半徑越小，增長率變化范圍越大，具有負增長率的小晶粒，其半徑越小，負增長率越大，說明半徑越小的晶粒越容易被周圍大晶粒吞噬。在Ⅱ、Ⅳ區域，仿真數據與Hillert理論方程吻合較好，半徑大于臨界半徑的晶粒趨于長大，半徑小于臨界半徑的晶粒趨于收縮；在Ⅰ、Ⅲ區域，仿真數據與Hillert理論方程存在差異，這部分晶粒占11.95%。可見，在一定誤差范圍內晶粒長大速率與Hillert理論方程吻合，這與采用CA方法仿真結果[17]一致。

晶粒增長率與邊數的關系如圖5所示。圖5也可以分為 4 個區域：Ⅰ區域（n＞6，dR/dt≥0）、Ⅱ區域（n≤6，dR/dt≥0）、Ⅲ區域（n≤6，dR/dt＜0）和Ⅳ區域（n＞6，dR/dt＜0）。4個區域的分布頻率分別是 29.57%、35.33%、33.88%、1.22%。顯而易見，邊數大于6的絕大部分晶粒趨于長大，邊數小于6的晶粒部分趨于收縮部分趨于長大；邊數相同的晶粒，其增長率也不同，這是因為晶粒的長大情況受近鄰晶粒的影響，只有在演化過程中一直具有優勢的晶粒才能持續長大。邊數小于6的晶粒，其增長率波動范圍較大，這與圖4中晶粒半徑越小，晶粒增長率變化范圍越大相對應。這是因為晶粒邊數與晶粒半徑呈正相關，晶粒的邊數越小則半徑越小。

為進一步研究晶粒長大規律，有必要對不同生長特點的單個晶粒進行研究。在t=1 000 ts時，隨機選取9個不同特點的晶粒并監測其面積和邊數的變化，如圖6所示。圖6a為晶粒面積隨時間變化的軌跡。可見，隨著時間的演化，初始面積較小的晶粒在較短時間內消失了，與圖4中晶粒半徑越小、負增長率越大、越容易被周圍晶粒吞噬的結論相符；而初始面積較大的晶粒，一部分隨時間增大而增大，一部分隨時間先增大后減小甚至消失，這是由于在晶粒長大過程中，平均晶粒面積（圖6a虛線）隨時間不斷增大，開始時刻比平均晶粒面積大的晶粒，最終的晶粒面積會小于或等于平均晶粒面積，最后甚至消失；在演化初期即使晶粒面積相同，其面積變化的規律也不同，這與晶粒所處環境有關。還可以看到，在開始很短一段時間內，晶粒面積隨時間線性變化，這與采用MC方法仿真結果[18]吻合。

圖6b為晶粒邊數隨時間變化的軌跡。可見，隨著時間的演化，晶粒邊數的變化分為3種情況：先增大后減小、先減小再增大最后減小、一直減小直至消失。然而，無論哪種變化，演化后期的晶粒邊數總小于演化初期，這是因為在多晶體系中，曲率驅動晶粒不斷長大，晶界不斷減小使得總界面自由能減少的緣故。開始時刻邊數為7的晶粒最終消失了，與圖5中邊數大于6的部分晶粒呈負增長的結論相符。

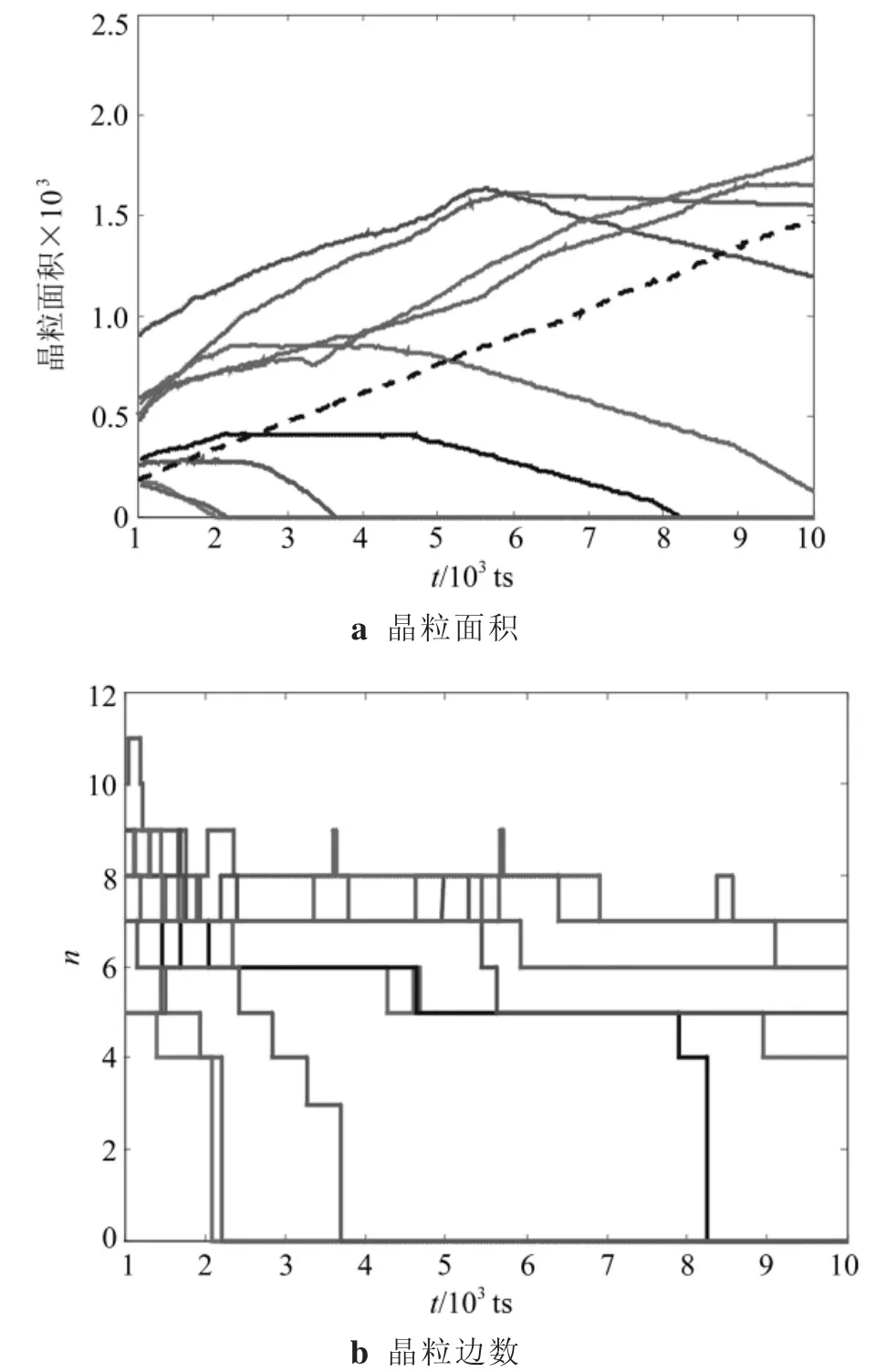
圖6 單個晶粒的面積和邊數隨時間變化的軌跡

從圖6中隨機選取單個晶粒面積隨邊數變化的軌跡如圖7所示。開始時刻的晶粒邊數最大，在晶粒長大過程中，晶粒面積變大，晶粒邊數減小；當晶粒面積達到最大時，晶粒邊數為6，超過該數據點后，晶粒趨于收縮（見圖7b），晶粒邊數變為3，最后晶粒消失。可見，在晶粒消失之前，晶粒邊數至少為 3，與文獻[11，18]的結論一致。

3 結論

（1）采用相場法大尺度模擬晶粒長大過程，得到的相對晶粒半徑分布和晶粒邊數分布較為穩定，均具有時間不變性；相對晶粒半徑分布的最大頻率在R/Rc=1附近，晶粒邊數絕大部分分布在4～8，并且晶粒邊數與半徑呈正相關。

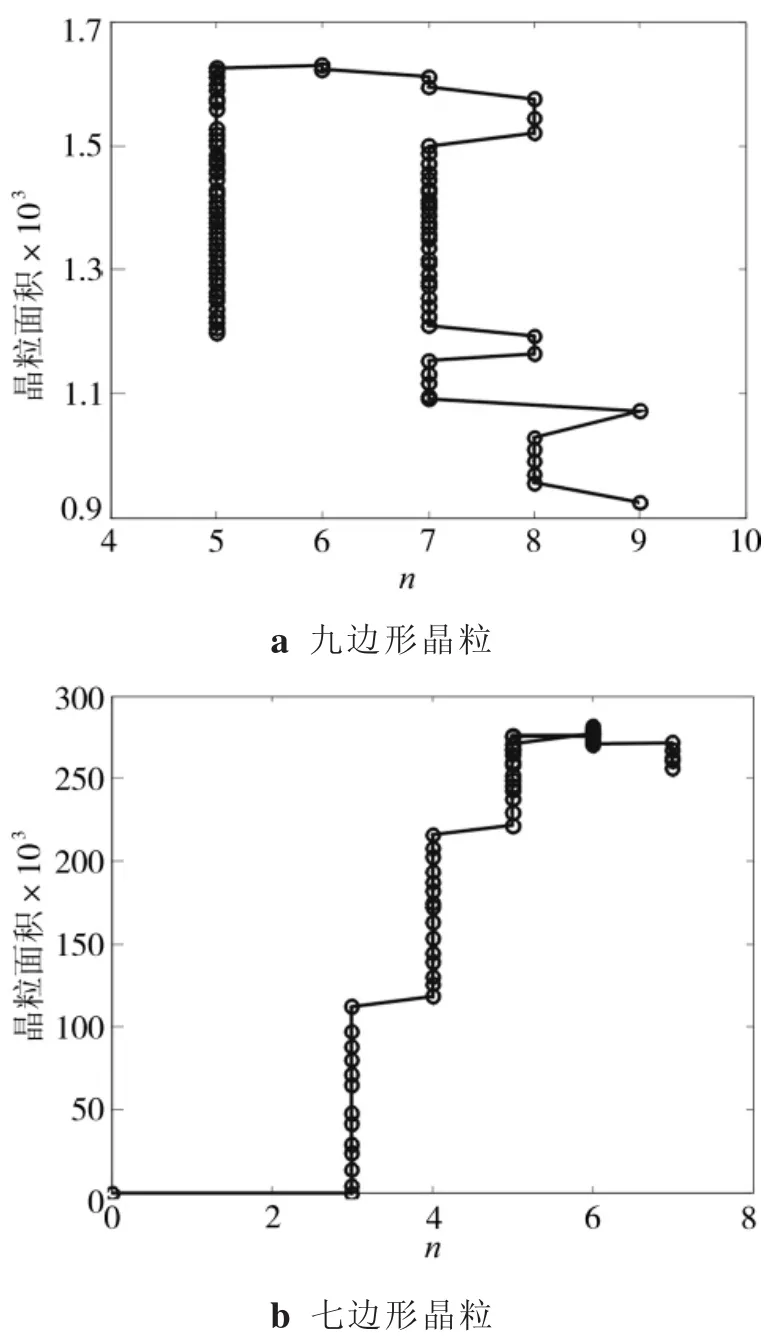
圖7 單個晶粒面積隨邊數變化的軌跡

（2）在單個晶粒長大動力學研究中，邊數大于6和半徑大于臨界半徑的絕大部分晶粒會長大，邊數小于6的晶粒增長率變化幅度較大，半徑小于臨界半徑的絕大部分晶粒會趨于縮小甚至消失。

（3）在一定誤差范圍內，單個晶粒長大速率和半徑的關系與Hillert理論方程吻合較好。