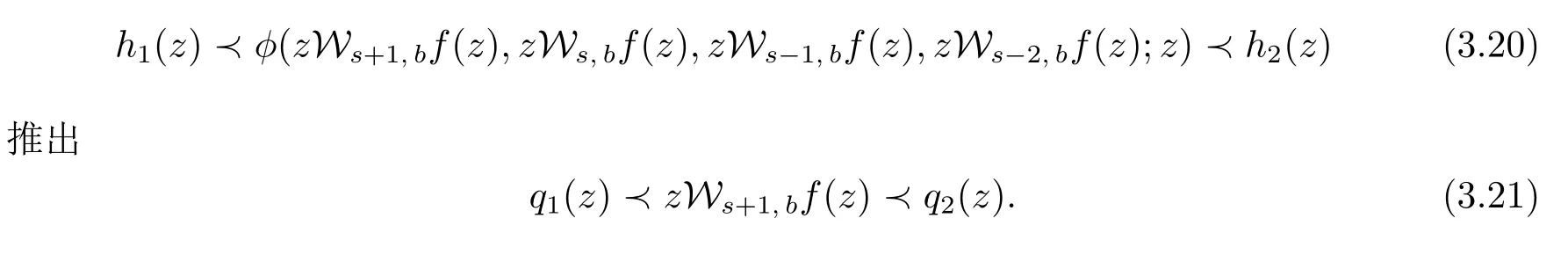某類包含Hurwitz-Lerch Zeta函數的三階積分算子

王小元,王知人,溫勝男,尹 櫪

(1.燕山大學理學院,河北秦皇島 066004)

(2.濱州學院數學系,山東濱州 256603)

1 引言

設H[a,n]為單位圓盤U={z:z∈C,|z|<1}中的解析函數類且具有如下形式為了方便,設H=H[1,1].

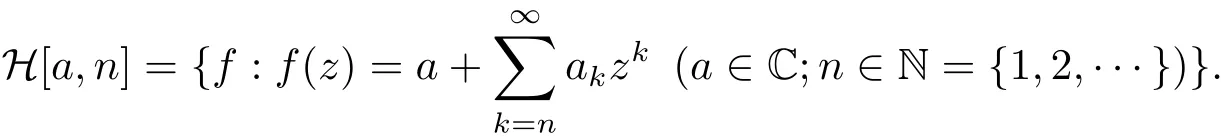
設f(z)和g(z)是U中的兩個解析函數,如果存在U內解析且滿足條件ω(0)=0和|ω(z)|<1的Schwarz函數,使得f(z)=g(ω(z))(z∈U)恒成立,稱函數f(z)在U中從屬于函數g(z),記為f(z)?g(z).相應地,稱g在U內超從屬于f.下列關系

是眾所周知的.更進一步地,如果g在U內單葉,則有下列等價關系

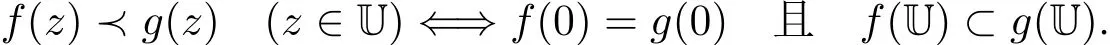
設Σ表示在去心單位開圓盤U?={z∈C,0<|z|<1}=U{0}內解析且具有如下形式

的函數類.

下面的函數Φ(z,s,a)稱為廣義的Hurwitz-Lerch Zeta函數(可參考文獻[1,2])

關于Hurwitz-Lerch Zeta函數Φ(z,s,a)的一些有趣的性質和特征可以參見最近的文獻,例如Choi和Srivastava[3],Srivastava等[4],Lin等[5]和Garg等[6].

利用Hurwitz-Lerch Zeta函數Φ(z,s,a),Srivastava和Attiya[7](也可參考文獻[8–11])引入和研究了下面的積分算子

類似于算子Js,bf(z),Wang和Shi[12]引入了積分算子

通過Hadamard卷積得到以下定義的形式

可以很容易從公式(1.1),(1.2),(1.5)和(1.6)中發現

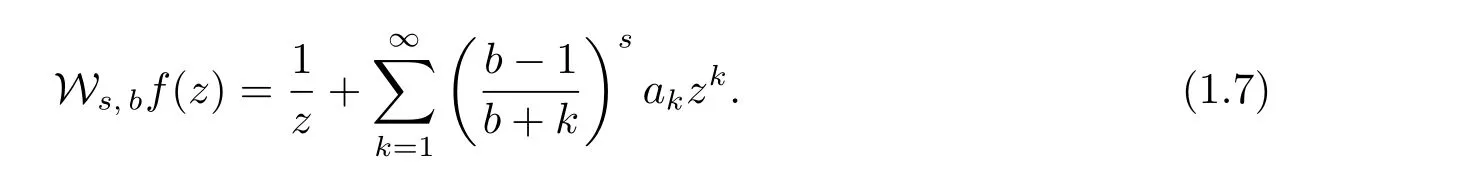
當b∈C{Z?∪{1}}時,算子Ws,b可以被定義為

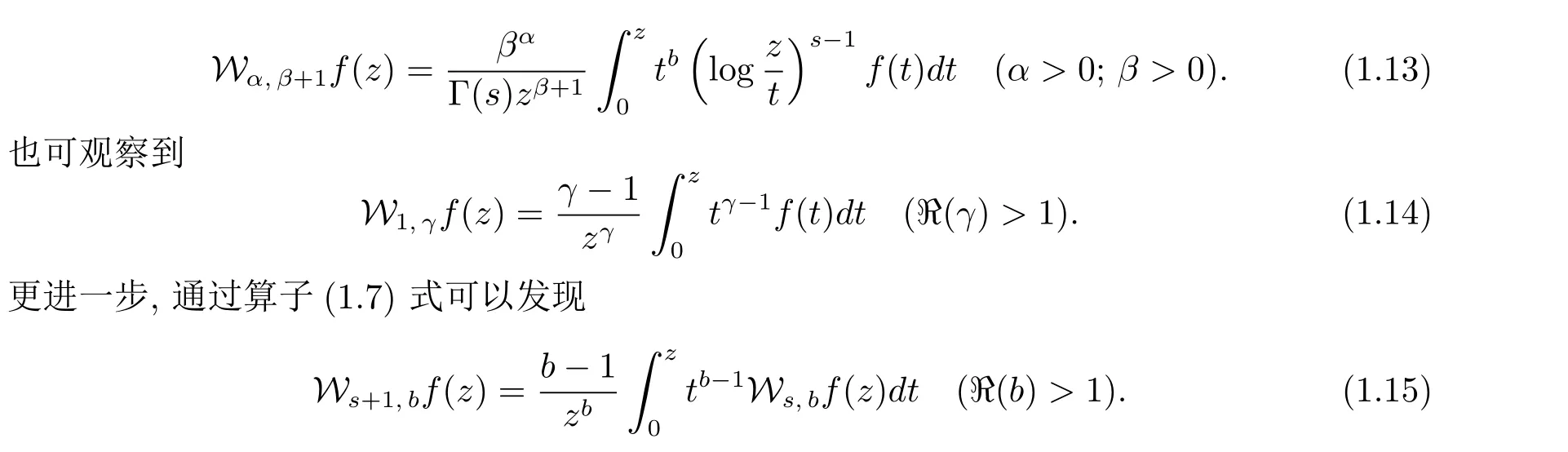
值得注意的是,算子(1.11)是被Alhindi和Darus[13]引入和研究的;算子(1.12)和(1.13)是被Lashin[14]引入和研究的.

本文的主要目的是通過研究算子Ws,bf(z)得出微分從屬,微分超從屬和Sandwich定理的相關結論.

2 預備知識

為了證明本文的主要結果,需要用到如下的定義和引理.

定義2.1[15]設Ψ:C4×U→C,函數q(z)和h(z)在U內單葉.若p(z)在U內解析且滿足三階微分從屬條件

則稱p(z)為上述微分從屬的一個解.如果對所有的解p(z),有p(z)?q(z),則稱q(z)為微分從屬解的一個控制.進一步,若存在一個控制eq(z)對所有適合(2.1)式的控制q(z)滿足eq(z)?q(z),則稱eq(z)為最佳控制.

定義2.2[15]設?為U的一個子集,函數q∈Q且n∈N{1}.又設ψ:C4×U→C滿足如下的允許條件

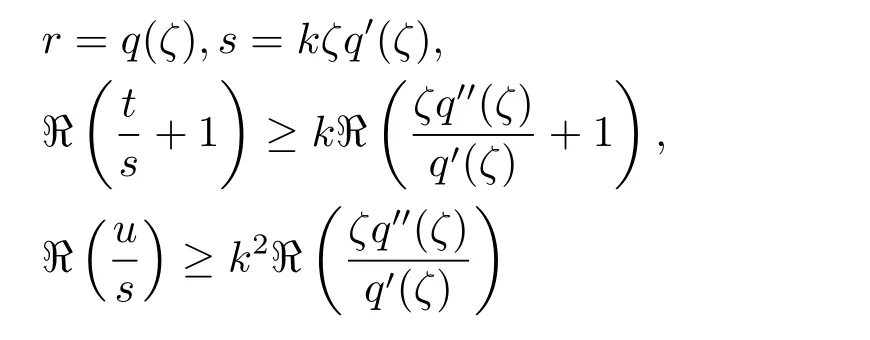
時,ψ(r,s,t,u;z)/∈?成立,其中z∈U;ζ∈?UE(q)和k≥n.稱上述函數ψ的集合為允許函數類,記作Ψn[?,q].

類似于Miller和Mocanu[16]引入的二階微分超從屬,Tang等[17]給出如下三階微分超從屬定義.

定義2.3[17]設ψ為C4×U→C的映射，函數h(z)在U內解析.如果p(z)和

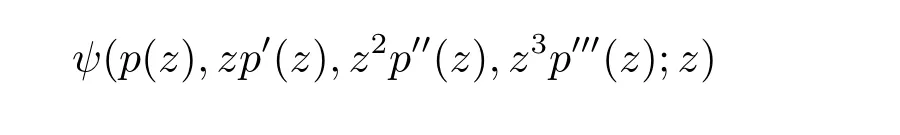
在U內單葉且滿足三階微分超從屬

則稱p(z)為上述微分超從屬的一個解.若對所有的解p(z),有q(z)?p(z),則稱q(z)為微分超從屬的一個從屬子.進一步,若存在一個單葉從屬子qe(z)對所有適合(2.2)式的從屬子q(z),均有q(z)?則稱為最佳從屬子.

定義2.4[17]設?為C的子集,函數q∈H[a,n]且q0(z)6=0.又設函數ψ:C4×U→C滿足如下的允許條件:當

時,有ψ(r,s,t,u;z)∈?成立,其中z∈U,ζ∈?U和m≥n≥2.則稱上述函數ψ的集合為允許函數類,記作[?,q].

關于微分從屬與微分超從屬的條件,本文選擇如下的允許函數.

定義2.5設?為C的子集且函數q(z)∈Q且q0(z)6=0.又設函數ψ:C4×→C滿足如下的允許條件:當

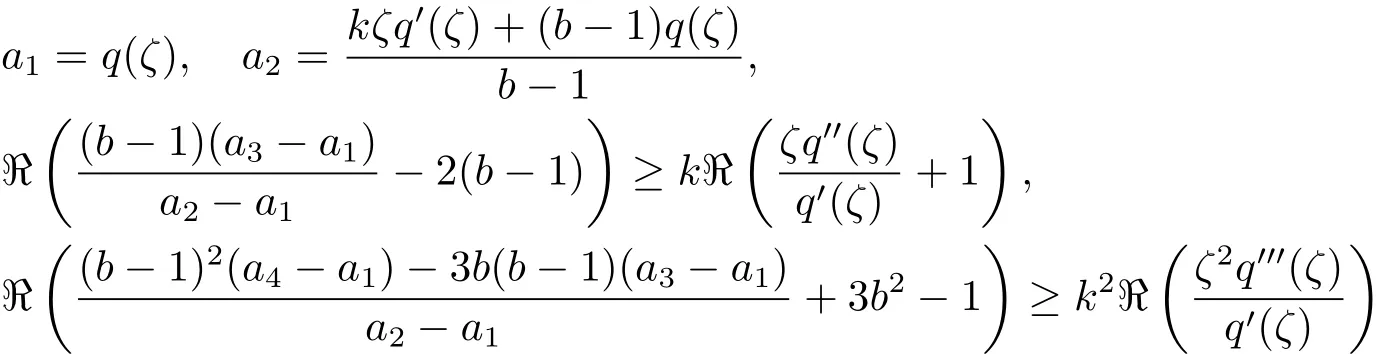
時,有φ(a1,a2,a3,a4;z)∈/?,其中z∈U,b∈C{∪{1}},s∈C,ζ∈?UE(q)和k∈N{1}.則稱上述函數φ的集合為允許函數,記作ΦΓ[?,q].

定義2.6 設?為C的子集且函數q(z)∈H且q0(z)6=0.又設函數ψ:C4×U→C滿足如下的允許條件:當

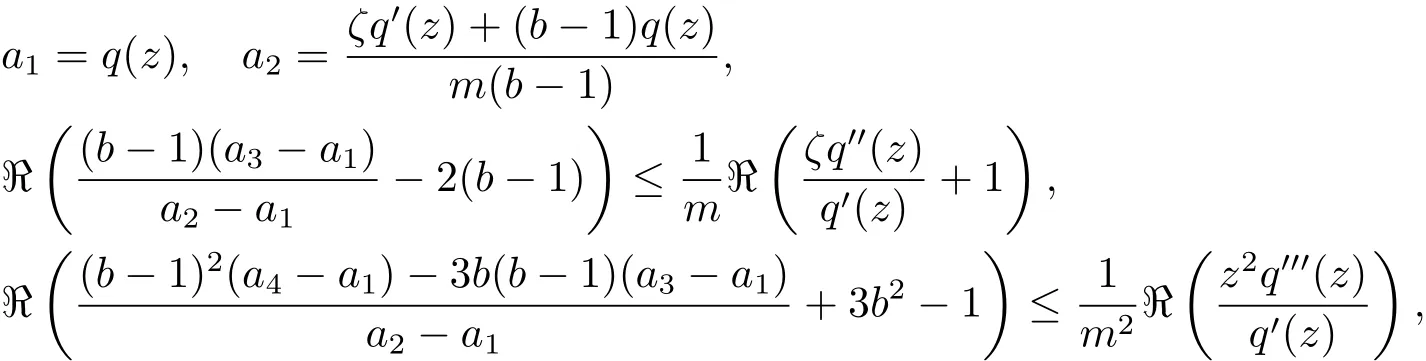
則有φ(a1,a2,a3,a4;ζ)∈ ?,其中z ∈ U,b∈ C{∪{1}},s∈ C,ζ∈ ?UE(q)和m ∈ N{1}.則稱上述函數φ的集合為允許函數類,記作[?,q].

引理2.1[15]設p(z)∈H[a,n],n∈N{1},函數q(z)∈Q(a)且滿足條件

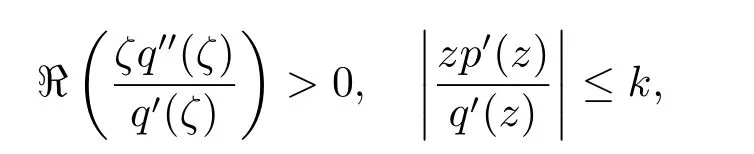
其中z∈U;ζ∈?UE(q)且k≥n.如果?是C的一個子集,滿足條件ψ∈Ψn[?,q]和

則p(z)?q(z).

引理2.2[17]設q(z)∈H[a,n]和ψ∈[?,q].如果ψ(p(z),zp0(z),z2p00(z),z3p000(z);z)在U中單葉,且滿足條件

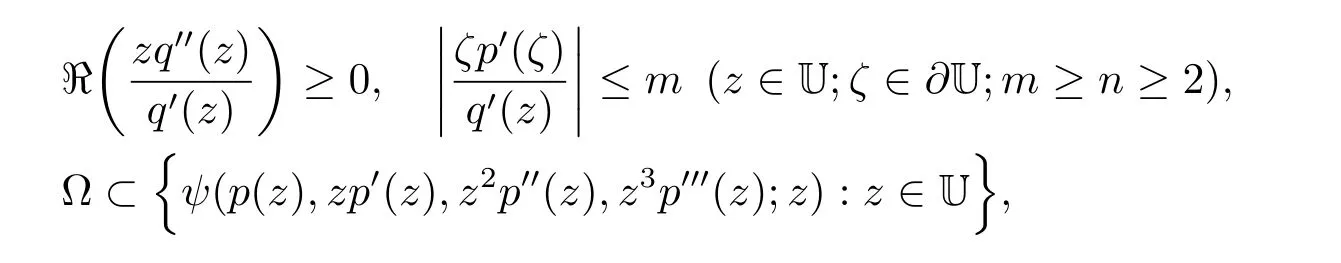
則q(z)?p(z).

3 主要結果

本文研究關于算子Ws,bf(z)的微分從屬與超從屬的亞純函數的性質,進而得到Sandwich型雙從屬結果.

定理3.1 設φ∈ΨΓ[?,q].如果f(z)∈Σ和q(z)∈Q1滿足條件

所以在定義2.5中當φ∈ΦΓ[?,q]時,結果可被證明.也可等價的看作ψ在定義2.2的條件n=2時可證明結果.注意到

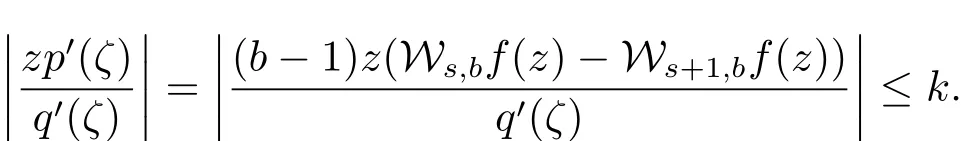
因此ψ∈Ψ2[?,q]且通過引理2.1,得到定理3.1.

如果? 6=C是一個單連通區域,且?=h(U)對U中的一些共形映射h(z)到?,則函數類ΦΓ[h(U),q]被看作ΦΓ[h,q].可以得到以下結果.

推論3.1 設φ∈ΦΓ[h,q].如果f(z)∈Σ和q(z)∈Q1滿足條件

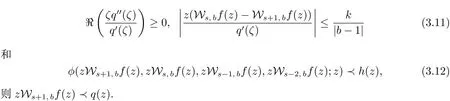
下面的推論是定理3.1的推廣,其中q(z)在U的邊界?U是未知的.

推論3.2 設??C,q(z)在U中單葉且q(0)=1.又設σ∈(0,1)對φ∈ΦΓ[?,qσ]成立,其中qσ(z)=q(σz).如果函數f(z)∈ Σ 滿足

則zWs+1,bf(z)? q(z),其中z∈ U,ζ∈ UE(qσ).

證 通過定理3.1,可以得出zWs+1,bf(z)?qσ(z).因此從qσ(z)?q(z)可以得到結果的證明.

推論3.3 設??C,q(z)在U中單葉且q(0)=1.又設σ∈(0,1)對φ∈ΦΓ[?,qσ]成立,其中qσ(z)=q(σz).如果函數f(z)∈ Σ 滿足

則zWs+1,bf(z)? q(z),其中z∈ U,ζ∈ UE(qσ).

證 設函數p(z)和ψ分別被(2.1)式和(3.9)式定義.因為φ∈Φ0Γ[?,q],所以從 (3.10)式和(3.18)式推出

如果? 6=C是一個單連通區域,且?=h(U)對U中的一些共形映射h(z)到?,則函數類[h(U),q]被看作[h,q].可以得到以下結果.

推論3.4 設φ∈Φ0Γ[h,q]且h(z)在U中解析.如果函數f(z)∈Σ,zWs,bf(z)∈Q1和

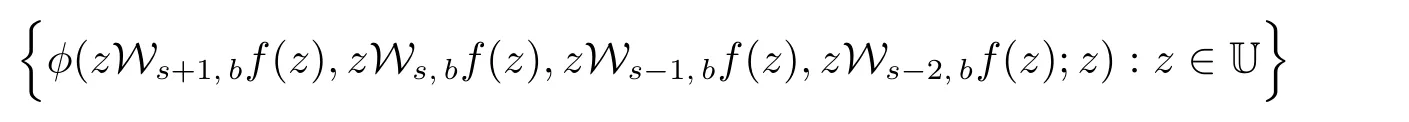
是單葉的,且

結合推論3.1和推論3.4,得到下面的Sandwich型雙從屬結果.

推論3.5 設h1(z)和q1(z)在U中解析,h2(z)在U中單葉,q2(z)∈Q1且q1(0)=q2(0)=1,φ ∈ ΦΓ[h,q]∩[h,q].如果函數f(z)∈ Σ,zWs+1,bf(z)∈Q1∩H 和

在U中單葉,且滿足條件(3.11)式和(3.17)式,則可由