混凝土細觀結構的數值模擬研究
宋來忠 廖大乾
(三峽大學 理學院, 湖北 宜昌 443002)
混凝土可視為由大量隨機分布的增強顆粒—骨料以及沙子和水泥所組成的混合物—砂漿所組成的多相復合材料.起初,人們先假設增強顆粒形狀為球形來進行計算機模擬.由于增強顆粒形狀一般都不是球形,人們進一步假設顆粒形狀為橢球[1-2];還有學者將增強顆粒的形狀假設為廣義橢球體進行數值模擬[3].為了使所模擬的增強顆粒的形狀更加接近自然形狀,一些學者[4-6]假設顆粒為多面體,研究了“大量多面體隨機分布的空間區域”的計算機模擬.作者[7-8]使用自由曲線曲面變形技術,將橢球變形得到了更加接近自然增強顆粒形狀的形體,去掉了一些學者在研究中的“凸性”限定條件,并且給出了這種顆粒形體的參數方程,得到了更加接近實際的混凝土材料的細觀結構.但有一個問題:如此模擬的顆粒過于不規則,以至于難以確定它的內部與外部.由于星形不一定是凸的,但卻可以判斷其內部與外部;所以,本文在文獻[7-8]的基礎上,對顆粒的形狀給出一定的限制,使其成為星形,直接給出空間點與這類星形顆粒位置關系的判別法則、空間點與這類星形顆粒的距離的近似計算與誤差估計,使得顆粒的影響區域在試件創建中減小,顆粒在試件中的分布更加合理、密度加大,從而能創建出具有更高顆粒含量的模型試件.
1 基礎知識
1.1 星形的定義
定義1如果一個簡單閉區域Ω上至少存在一點0∈Ω,使得對任意P∈Ω都有直線段OP∈Ω,則稱Ω關于點O是星形.
顯然,所有的凸單連通的簡單閉區域都是星形.如果用I(Ω)表示區域Ω的內部,E(Ω)表示區域Ω的外部,?Ω表示區域Ω的邊界,假如Ω關于點O是星形的,那么對空間中任意一點,過P的直線與Ω邊界的?Ω交點不超過2.并且易得如下判定定理.
定理1設Ω為關于點O是星形的,若空間任意點P0(x0,y0,z0)與O的連線交邊界?Ω于P1(x1,y1,z1),P2(x2,y2,z2)兩點,那么
(1)
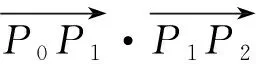
1.2 星形參數化描述及條件
作者在文獻[8]引入了一種新的伸縮因子函數,下面將要使用這個伸縮因子將橢球變形.
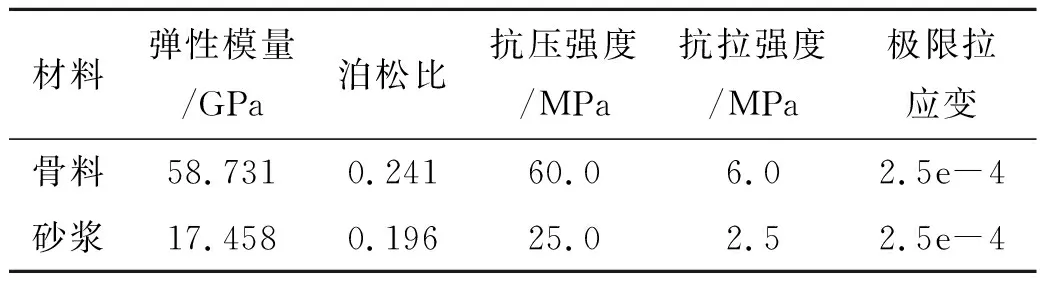
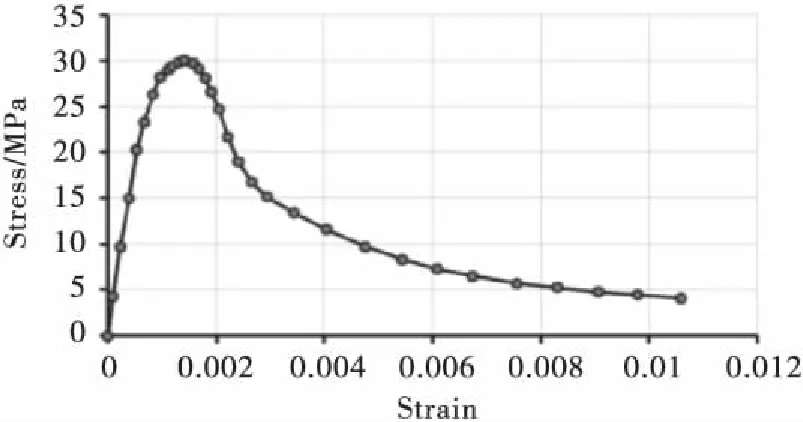
定義2設0 令 t=(u-u0)2+(v-v0)2(2) 作R2上的連續函數: (3) 令 (4) 則B(u,v)被稱為是R2上的基本伸縮因子.其中Ω1是峰值區域,而Ω2為變形區域. 橢球面的參數方程可表示為: (5) 其中I=[0,2π]×[0,π],T=(tij),i,j=1,2,3,且t11=cosφcosψ-sinφcosθsinψ,t12=cosφsinψ+sinψcosθcosφ,t13=sinφsinθ,t21=-sinφcosψ-cosφcosθsinψ,t22=-sinφsinψ+cosφcosθcosψ,t23=cosφsinθ,a31=sinθsinψ,t32=-sinθcosψ,a33=cosθ.而θ,φ,ψ為歐拉角,且θ∈[0,π),ψ∈[0,2π),φ∈[0,2π).P(u,v)為定義在參數(u,v)平面R2中區域I上的光滑曲面. 設變形中心為O′的取峰值區域Ω1和支區域Ω2(Ω1?Ω2?Ω).取伸縮系數α1,α2,α3∈R,伸縮系數矩陣記為D=diag(α1,α2,α3),豐滿指數k取為正整數.那么,變形之后的參數曲面Pd(u,v)與變形之前的橢球面P(u,v)就有如下關系: Pd(u,v)=(DB(u,v)k+E)(P(u,v)-O′)+O′, (u,v)∈I(6) 顯然,邊界曲面可由(7)表示的區域,不一定是星形區域.但實際上,有 定理2如果取O′=O,只要αi≥-1,i=1,2,3.那么,邊界為(7)的Ω關于點O為星形區域. 滿足定理2條件的方程(7)的空間圖形是星形(如圖1所示). (u,v)∈I(7) 其中,在第i個變形的區域中,峰值區域為Ω1i,支區域為Ω2i,它們分別為: 由于伸縮系數矩陣Di=diag(α1i,α2i,α3i)的所有元素都是大于等于-1的,故對于空間點P′(x′,y′,z′)=P′(x′(u′,v′),y′(u′,v′),z′(u′,v′)),可考慮函數: g(u′,v′)= 那么,有 定理3設P′是空間中任意一點,那么 (10) 定義3空間中任意一點P′(x′,y′,z′)到?Ω的距離,可以定義為 (11) (u,v)∈I(12) 其參數區域是閉區域I=[0,2π]×[0,π],所以可以考慮如下快速的搜索法算法: 第1步:給定自然數n,取ui+1=2iπ/n,vj+1=jπ/n;i=0,…,n-1,j=0,…,n-1 第2步:由式(8)計算星形表面上對應的n2個點:Pd(x(ui,vj),y(ui,vj),z(ui,vj)) 第3步:將上一步得到的n2個點的坐標,代入目標函數,計算n2個函數值:f(x(ui,vj),y(ui,vj),z(ui,vj)) 第4步:取min{f(x(ui,vj),y(ui,vj),z(ui,vj))} 作為所求距離d(P,?Ω)的近似值. 定義4空間中任意一點P′到Ω的距離,可以定義為 (13) 如圖2所示.誤差滿足 可得距離的誤差范圍: (14) 圖1 橢球變為星形 圖2 點到骨料的距離誤差圖 以試件中需生成的星形總個數的最大值N、或者試件中需生成的星形的總體積數S(星形體積的計算見文獻[8])、或者模擬時搜索中心連續被拒絕總次數K,來控制終止.用k記連續選取中心點O而被拒絕的次數;用n記已生成的星形個數;用s記已生成的星形的總體積數.主要步驟如下. 第1步:設定產生隨機星形的各種參數及其分布區域、試件中星形的總個數最大值N、星形的體積總數S以及搜索中心連續被拒絕總次數K,給初值n=1,k=0,s=0; 第2步:根據顆粒半徑的范圍,隨機產生一個數a; 第3步:在模擬區域內隨機選取一點O(x0,y0,z0),判斷它是否是在所有已生成的星形顆粒的外部;若否,則令k=k+1,轉到第4步;若是,由計算距離的搜索算法計算O與所有的已生成星形顆粒之間的距離,并判斷最小的距離d是否≥a(注意控制誤差);若否,則令k=k+1,轉到第4步;若是,則取橢球的中心為O(x0,y0,z0),長半軸長為a,生成一個橢球,再將橢球隨機變形,使之成為星形顆粒,并計算星形的體積s0,令s=s+s0,n=n+1,到到第4步; 第4步:如果滿足n>N,或k>K,或s>S,結束程序;否則,轉到第2步. 由于界面和骨料的尺度差異太大,受計算工具的限制,難以用有限元方法對其進行力學分析計算.所以,本文采用其他一些學者的做法[4-6,9],假設混凝土是具有星形增強顆粒以及砂漿所組成的兩相復合材料,伸縮系數控制在-0.16~-0.1之間.然后,根據文獻[10]所給的級配曲線模擬生成混凝土試件,如圖3、圖4所示. 圖3 骨料含量為55%的 圖4 骨料含量為60%的二級配隨機模擬 三級配隨機模擬 圖3是假設增強骨料形狀為星形,模擬的骨料含量為55%的二級配混凝土試件,模擬區域為[0,15]×[0,15]×[0,15](單位:cm),顆粒粒徑為0.5∶2,2∶4兩種級別.兩種骨料的體積分別是:839.165 6 cm3和1 017.202 2 cm3,所有骨料的總體積為1 856.367 8 cm3占到試件體積的55%.兩種骨料的配合比大約為4.5∶5.5.每種骨料顆粒數為3 527和130,骨料顆粒總數為3 657. 圖4是假設增強骨料形狀為星形,模擬的骨料含量為60.04%的三級配混凝土試件,模擬區域[0,30]×[0,30]×[0,30](單位:cm),顆粒粒徑分別為0.5∶2,2∶4和4~8三種.每種骨料的體積分別為:4 050.08 cm3,4 864.87 cm3和7 295.18 cm3,骨料總體積為16 210.15 cm3占試件總體積的60.04%.3種骨料的配合比約為2.5∶3∶4.5.每種骨料個數為5 128和229,33,骨料顆粒總數為5 380.顯然,比文獻[8]的算法生成試件的骨料含量高. 值得注意的是:誤差估計式(14),必須充分大才能成立,但n若取得太大,會影響計算速度.所以,在作模擬時,一定要注意檢查,以便選取適當的n值. 本文選擇背景網格剖分,網格全部采用Abaqus軟件中的C3D8R類型單元劃分.將正方體的8個頂點作為背景網格的基本點來判斷,如果8個頂點有5個都屬于骨料單元,則這8個點組成的網格單元屬于骨料單元,否則,這8個點組成的網格單元屬于砂漿單元. 以圖3骨料含量為55%的幾何模型為例,對15 cm×15 cm×15 cm區域的用背景網格劃分,將其邊界其以3 mm為步長,分成50等分,共125 000個網格單元.得到的骨料單元51 284個,砂漿單元73 716,其中骨料的網格單元的含量為41%.如圖5~7所示.要說明的是:選用背景網格,當幾何模型離散成有限元單元之后,一些較小的骨料,將會被砂漿“融掉”所以會降低骨料的含量. 圖5 砂漿背景網格圖 圖6 骨料背景網格圖 圖7 砂漿和骨料混合的背景網格圖 下面采用Abaqus軟件中混凝土塑性損傷模型的本構關系[9],對上述有限元模型,進行力學分析試算.材料參數按文獻[10]選取,如表1所示. 表1 混凝土材料力學參數 對上述有限元模型試件底部添加固定約束,如圖8所示.為了方便處理,在試件的上端添加了一個參考點RP1,然后對頂部的上表面第一層與該點進行全約束,保證頂部均勻受力,同時通過該點來體現整個試件的應力與應變的關系[11],如圖9所示. 圖8 試件底部約束圖 圖9 試件頂部約束圖 然后,在試件的頂部施加的是方向向下的2 mm的位移荷載,得到試件受力過程的應力分布云圖結果如圖10所示.加載結果的破壞過程如圖10所示.圖10(a)表示在沒有加外力的作用下,混凝土試件的初始狀態.圖10(b)表示的是混凝土試件局部區域開始出現損傷單元.圖10(c)表示混凝土試件的頂面所受的應力表現的不如正面的應力那么明顯,其中正面的應力比較集中,逐漸呈現出“X”形狀的趨勢.從圖10(d)可以看出,隨著荷載的施加,試件損傷單元沿試件45度方向慢慢擴展,最終形成一條宏觀裂縫.圖10(e)表示的是在極限應力作用下,兩個受力面的三維視圖,其中兩個應力面均顯示了混凝土試件的損傷單元都是沿著45°方向擴展.這與文獻[12]報道的真實的混凝土試件在受壓狀態下的損傷結構基本一致. 圖10 三維混凝土試件單軸壓縮破壞損傷過程圖 對比圖11和Abaqus手冊[9]中的標準混凝土單軸壓縮損傷圖像圖,可以看出兩者變化趨勢基本一致. 圖11 應力應變關系圖 本文在文獻[7-8]的基礎上,對復合材料的增強顆粒的形狀給出一定的限制,使其成為星形,創建出比以往文獻中報道的顆粒含量更高的試件.為進一步從細觀力學的角度,分析具有增強顆粒的復合材料的性能,提供了創建更加接近真實試件的幾何模型方法.從理論上來說,本文的方法也是文獻[13]的三維推廣.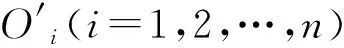
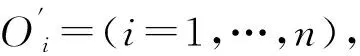
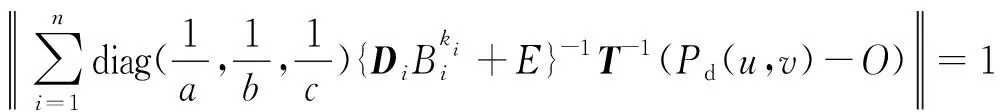
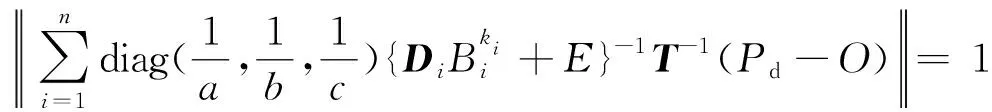
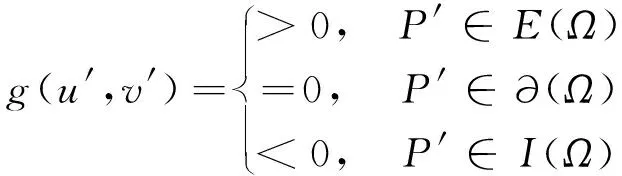
1.3 點到星形體的距離計算的搜索算法及誤差
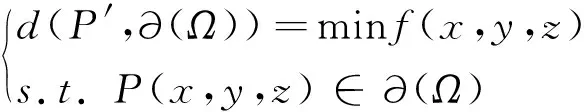
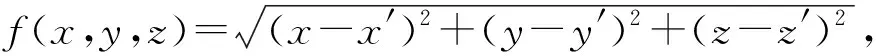
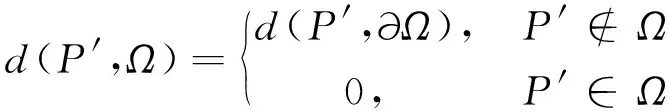

2 基本算法
3 混凝土數值模擬實例

4 有限元網格模型實例

5 力學分析模擬試算


6 結 語

