一個4-D超混沌系統的特性分析及混沌控制設計

梁 媛 王仁明，2 王凌云，2

(1. 三峽大學 電氣與新能源學院， 湖北 宜昌 443002； 2. 三峽大學 網絡與智能控制研究所， 湖北 宜昌 443002)

超混沌系統一般可以定義為至少存在兩個正Lyapunov指數的混沌系統[1]，因而超混沌系統有更復雜的動態行為，如多渦卷混沌吸引子、多個正Lyapunov指數、截面上的Poincare映射非孤立等，這使得對超混沌系統的研究成為極具挑戰性的課題．第一個典型的超混沌系統是Rossler超混沌系統[2]，接著其它一些超混沌系統相繼出現了，如Chen超混沌系統[3-4]、Lu超混沌系統[5]、Nikolov超混沌系統[6]、Lorenz超混沌系統[7-8]等．

由于混沌系統在許多領域有著明顯或潛在的應用，如：保密通訊[9-10]，密碼系統[11-12]，加密術[13-14]，電子電路[15-16]等，在過去的20年中，對混沌系統的控制研究受到了極大的關注，出現了許多控制方法：最優控制方法[17-18]，自適應控制方法[19]，滑模控制方法[20]，時滯反饋控制方法[21]等．

基于超混沌系統豐富的動力學特性和實用性，為了更好地對動力學特性進行分析與控制設計．本文討論了一個新型四維超混沌系統的動力學特性及控制問題．首先，分析了系統的一些動力學特征，如耗散性、時間序列、相軌跡圖、李雅普諾夫指數譜和龐加萊映射．接下來，應用Lyapunov穩定理論分析了超混沌系統的自適應控制問題，并對具有完全未知參數的四維超混沌系統設計了一個參數估計的自適應律．最后，利用Matlab仿真軟件對所有設計結果進行了仿真驗證，闡述了分析和設計的正確性和有效性．

1 系統描述及混沌特性分析

1.1 系統描述

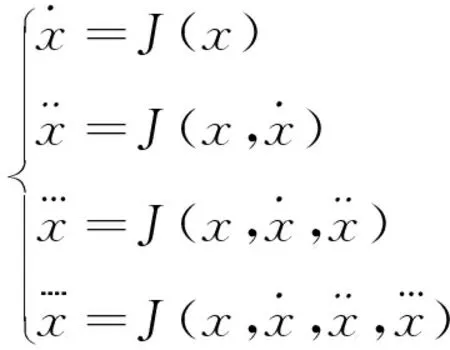
(1)

故本文考慮如下新型四維超混沌系統：

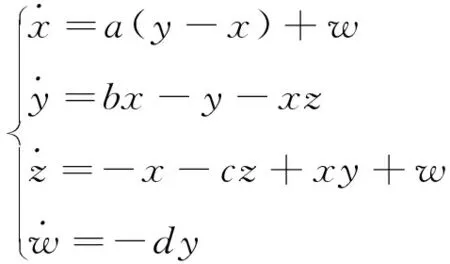
(2)

其中，x，y，z，w為狀態變量，a，b，c，d為系統的正常數參量．

1.2 相軌跡和時間序列

當系統參數分別為以下數值時，該四維系統是超混沌的

a=24，b=125，c=5，d=10 (3)

使用Wolf算法計算可知，系統(2)的Lyapunov指數為：L1=2.946，L2=2.083，L3=-2.432，L4=-32.59．由于系統的Lyapunov指數中有兩個是正數，說明該新型四維系統是超混沌的．此時，系統(2)的Kaplan-Yorke維數為：

可知系統(2)有一個分數Kaplan-Yorke維數的奇異吸引子．

若取系統(2)的初始狀態為：

x(0)=y(0)=z(0)=w(0)=0.2 (4)

則系統的相圖、時間序列圖及Lyapunov指數譜分別顯示在圖1、圖2和圖3中．

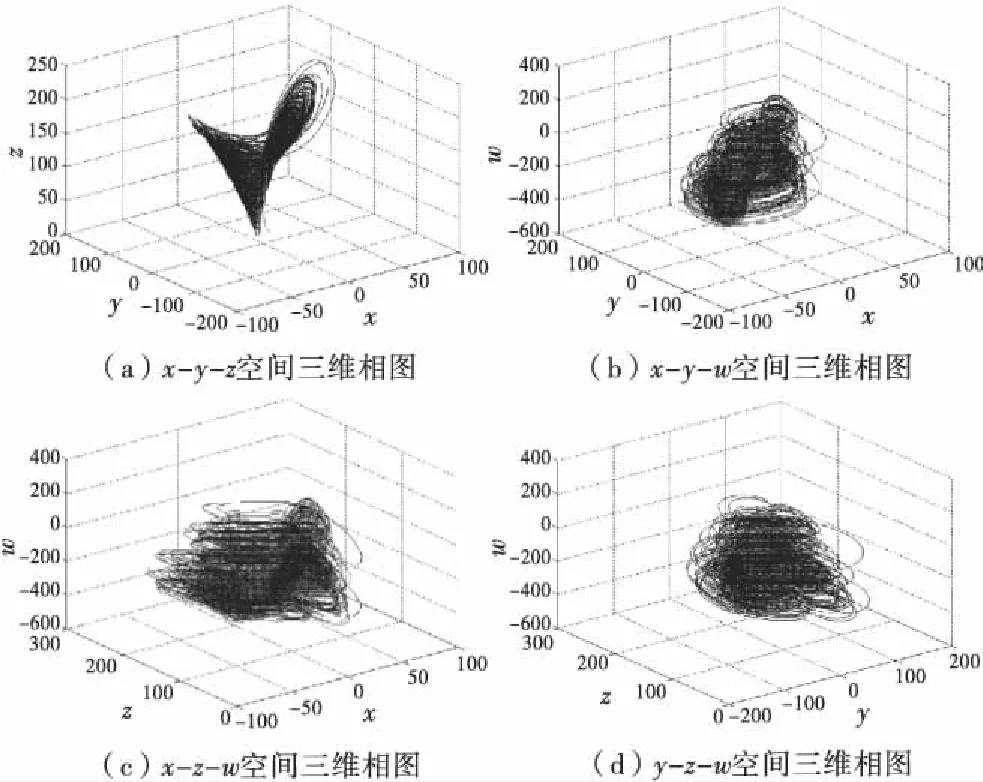
圖1 四維超混沌系統的相圖

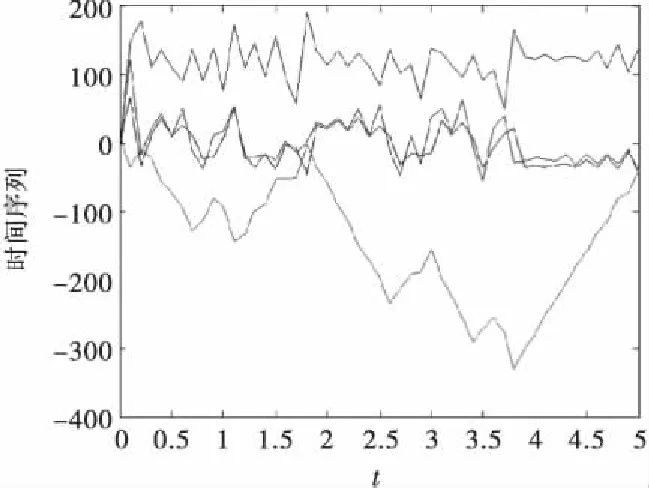
圖2 四維超混沌系統的時間序列圖

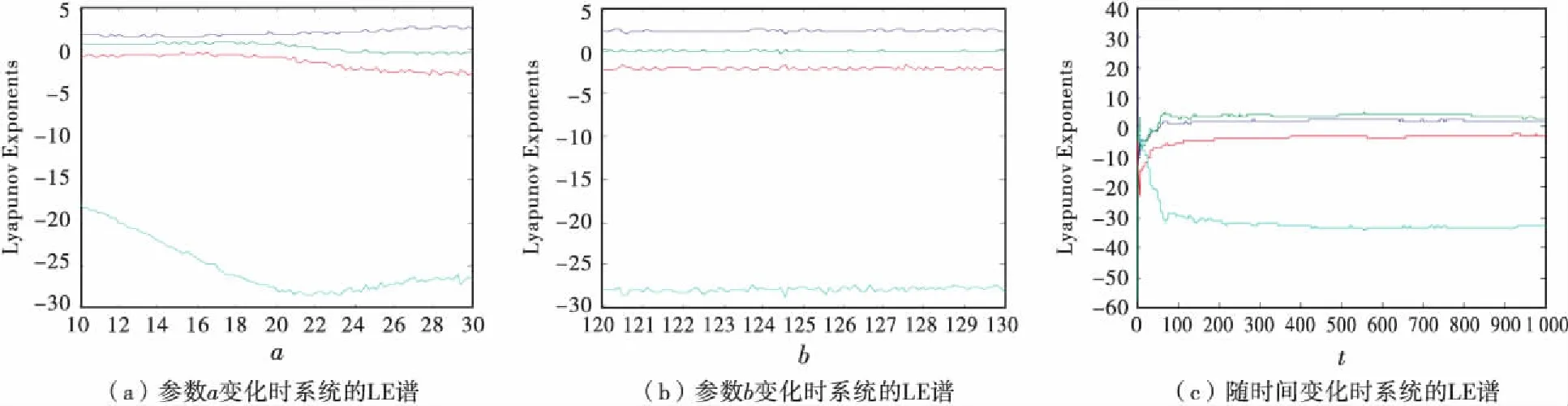
圖3 四維超混沌系統的Lyapunov指數譜

1.3 耗散性

超混沌系統(2)可以用向量表示為：

(5)

其中，

(6)

通過Liouville定理，可知

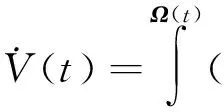
其中向量Ω(t)=Φt(Ω)，Φt是f的通量，V(t)為Ω(t)的體積．

系統(2)的散度為：

(8)

其中μ=a+1+c．

根據式(3)中選擇的參數值，知μ=30>0，將式(8)里·f的值代入到式(7)中，可得

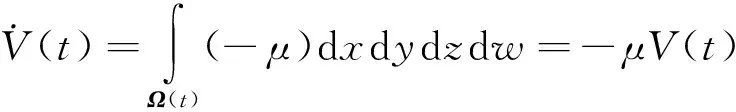
(9)

即

V(t)=exp(-μt)V(0) (10)

由于μ>0，從式(10)可知，當t→∞時，V(t)以指數方式趨于0．這顯示系統(2)是耗散的．因此，其軌線最終被限定于一個零體積的子集內，并且其漸近運動將止于一個奇異吸引子上．

1.4 平衡點

當系統(2)的參數值如(3)中所示時，平衡點可由解下列等式獲得：

(11)

即

系統(2)在F∈R4的任一點的雅可比矩陣為：

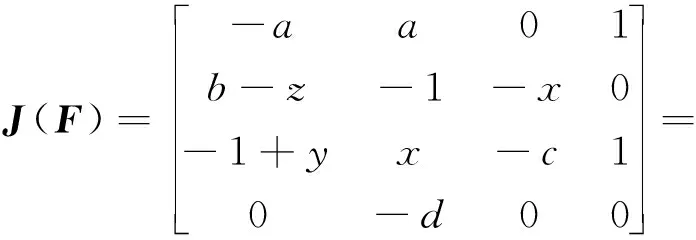
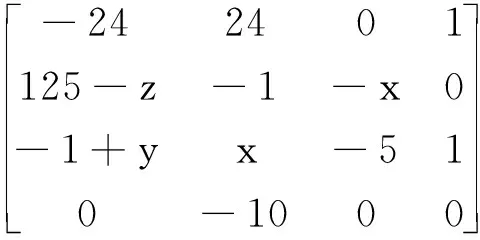
在平衡點E0的雅可比矩陣為：

(14)

雅可比矩陣J0的特征值數值為：

λ1=-5，λ2=-68.629 0，λ3=0.421 5，λ4=43.207 4 (15)

因此，平衡點E0是不穩定的鞍點．

在平衡點E1的雅可比矩陣為：

(16)

雅可比矩陣J1的特征值數值為：

λ1=-0.362 4，λ2=-23.429 4，

λ3，4=-3.466 5±26.906 7i(17)

因此，平衡點E1也是不穩定的鞍點．

1.5 龐加萊映射

龐加萊映射是一種有助于形象化混沌折疊特性的分析技術．當參數a=24，b=125，c=5，d=10時，在不同的交叉平面，如x=0，z=32，在圖4中顯示了x-y、y-z和y-w平面對應的龐加萊映射圖．

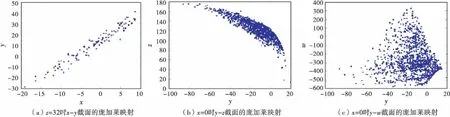
圖4 四維超混沌系統的龐加萊映射圖

2 4-D超混沌系統的自適應控制

目標是尋找四維超混沌系統(2)的一種具有參數估計值更新規律的自適應控制，使得當t→∞時，所有狀態變量x、y、z、w都收斂于系統的平衡點．

假設受控的系統為：

(27)

其中，x，y，z，w為系統的狀態變量，且a，b，c，d為未知的參量．V1、V2、V3、V4為待設計的自適應控制器．

若系統(2)的參數是未知的，設計其自適應控制律為：

(28)

參數估計值更新律為：

(29)

這里，a1、b1、c1、d1為不確定參數a、b、c、d的估計值．li(i=1，2，3，…，8)為正常數．則在任意初始狀態(x(0)，y(0)，z(0)，w(0))∈R4下，具有未知參數的四維超混沌系統是全局漸近穩定的．

證明：將式(28)代入到式(27)中，可得到如下閉環系統模型：

(30)

定義李雅普諾夫函數為：

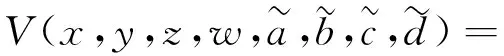
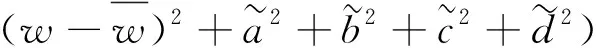
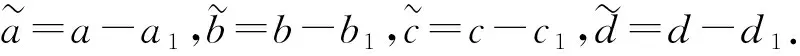
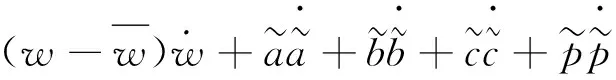
將式(29)、式(30)代入(32)中可得：

l7(c-c1)2-l8(d-d1)2

(33)

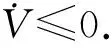
x(0)=2，y(0)=2，z(0)=2，w(0)=2，

a=24，b=125，c=5，d=10 (34)

取li=0(i=1，2，3，…，8)，并設參數的初值為0．狀態變量和參數估計值的運行軌跡仿真結果顯示在圖5和圖6中．

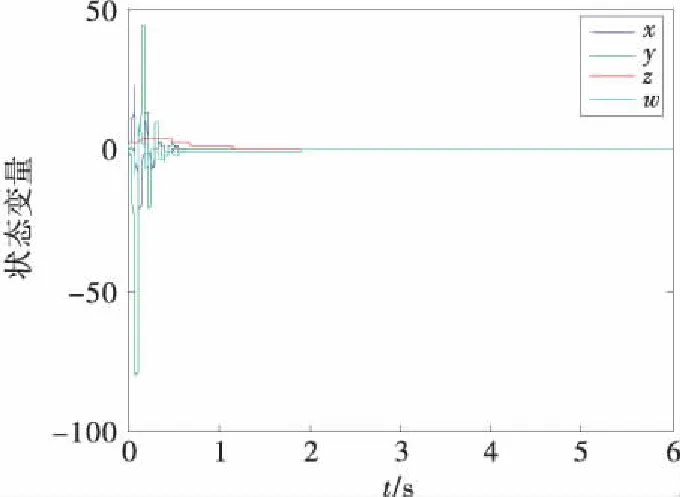
圖5 自適應控制狀態變量圖

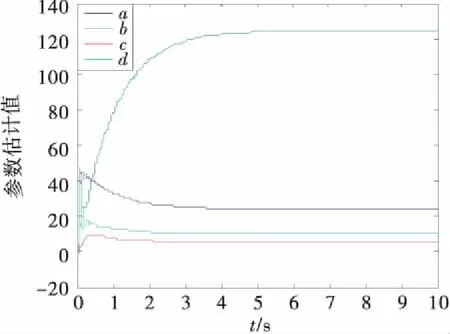
圖6 參數估計值更新圖

由圖5和圖6可看出，在自適應控制器的作用下，系統狀態變量迅速趨于平衡點E0(0，0，0，0)，且系統未知參數的估計值收斂于被給的參數值．說明該控制方法對多未知數的四維超混沌系統可以達到期望的控制效果．

3 結 論

本文討論了一個新型的四維超混沌系統的混沌特性，如耗散性、時間序列、奇異吸引子、李亞普諾夫指數譜、龐加萊映射等．同時，設計了自適應控制律來穩定具有未知參數的新型四維超混沌系統．其設計的有效性和正確性由數值仿真得到了驗證．