研究拋體運動的分解方法

武銀根

研究平拋運動時，通常把平拋運動分解成水平方向的勻速直線運動和豎直方向的自由落體運動，即使教師講解新課時，也是通過各種實驗來說明這種分解的意義，其實，把曲線運動分解成兩個直線運動是沒有規定的，取任意兩個方向都可以按照平行四邊形定則進行分解，因此研究平拋運動也就不一定沿水平和豎直兩個方向分解，二是根據需要取兩個方向進行分解，有時候方向取得好會使問題變得非常簡單.

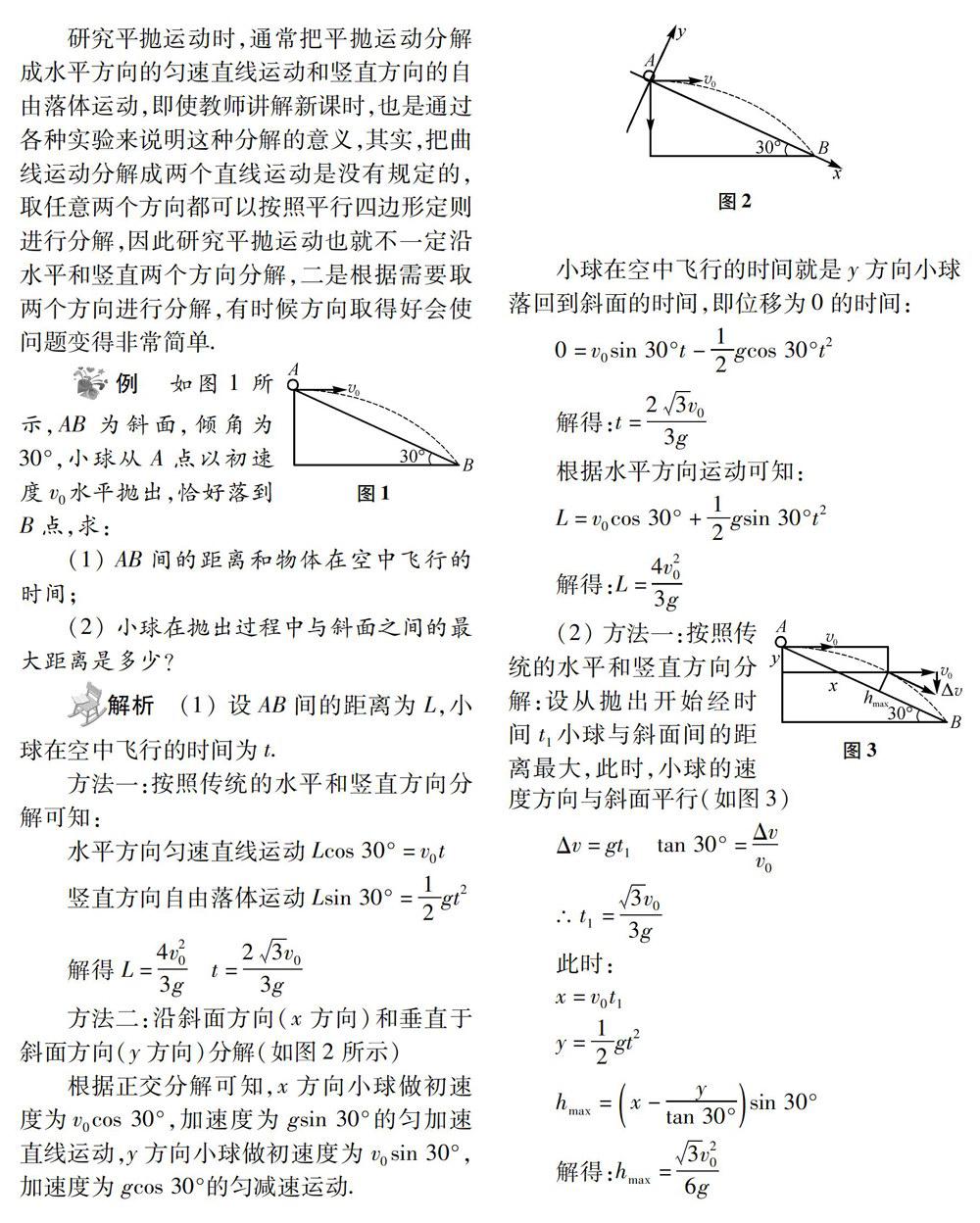
例 如圖1所示，AB為斜面，傾角為30°，小球從A點以初速度v0水平拋出，恰好落到B點，求：

（1） AB間的距離和物體在空中飛行的時間：

（2）小球在拋出過程中與斜面之間的最大距離是多少？

解析 （1）設AB間的距離為L，小球在空中飛行的時間為t.

方法一：按照傳統的水平和豎直方向分解可知：

方法二：沿斜面方向（x方向）和垂直于斜面方向（y方向）分解（圖2所示）：

根據題意可知，小球離開斜面的距離即為y方向運動的位移，根據y方向運動可知，最大位移時y方向瞬時速度為零，根據運動方程直接得：

從本例可以看出，研究平拋運動時不一定沿水平方向和豎直方向分解運動，只要運用平行四邊形定則，取任意兩個方向都可以進行分解，也就是根據需要進行分解，在與斜面相關的問題中，巧妙選擇分解的方法會使問題變得簡單，在研究斜拋運動時分解方法同樣是靈活的.

同樣，研究斜拋運動問題也可以按照需求進行分解，如：

如圖4所示，從A點以v0的初速度拋出一個小球，在離4點水平距離為s處有一堵高度為h的墻BC，要求小球能越過B點.問小球以怎樣的角度拋出，才能使v0最小？

解析 方法一：將斜拋運動分解成v0方向的勻速直線運動和豎直方向的自由落體運動的合運動，如圖5所示.

在位移三角形ADB在用正弦定理