基于柔性負(fù)荷的負(fù)荷特性分析和短期負(fù)荷預(yù)測新技術(shù)
丁小葉
?
基于柔性負(fù)荷的負(fù)荷特性分析和短期負(fù)荷預(yù)測新技術(shù)
丁小葉
(國網(wǎng)江蘇省電力有限公司南通供電分公司,江蘇 南通 226006)
根據(jù)電力需求的價格彈性分析了智能電網(wǎng)下負(fù)荷與電價之間的相關(guān)性。同時,將總負(fù)荷按照各影響因素進行分解,提出預(yù)測柔性負(fù)荷容量大小的方法:在傳統(tǒng)負(fù)荷預(yù)測因素的基礎(chǔ)上,考慮實時電價因素,提出基于電價敏感性負(fù)荷建模的短期負(fù)荷預(yù)測新技術(shù);對美國PJM市場下的某地區(qū)負(fù)荷進行算例分析。
柔性負(fù)荷;負(fù)荷特性分析;短期負(fù)荷預(yù)測;智能電網(wǎng)
智能電網(wǎng)的負(fù)荷預(yù)測需要站在市場的角度看待用戶的需求,綜合考慮電價、風(fēng)險、輸電能力等[1],傳統(tǒng)的負(fù)荷特性分析和單值負(fù)荷預(yù)測已無法滿足這類要求。文獻(xiàn)[2]對江蘇省部分地區(qū)的負(fù)荷特性進行分析,在負(fù)荷特性分析的基礎(chǔ)上對有關(guān)需求側(cè)管理措施的成本效益進行分析計算,比較了不同的用電設(shè)備參與需求側(cè)管理項目的規(guī)模大小及節(jié)電效果。
1 電價對負(fù)荷的影響分析
隨著電價升高,負(fù)荷需求隨之減小,負(fù)荷需求量與電價成反比,通常將其在某一均衡點附近線性化,定義為彈性系數(shù),公式為:

式(1)中:為彈性系數(shù);△為負(fù)荷變化量;△為電價變化量。
由不同時刻的彈性系數(shù)組成的矩陣稱為彈性矩陣,比如每日24 h的需求實時電價彈性,其矩陣為:

在矩陣中,對角線上的彈性系數(shù)為負(fù)值,表示單個時段負(fù)荷隨電價變化的彈性;其余的彈性系數(shù)為非負(fù)值,表示跨時段負(fù)荷電價彈性。不同電力用戶價格彈性矩陣也不同,比如大用戶(工業(yè))可通過多種形式參與市場,彈性系數(shù)較大;而中小用戶(商業(yè)、居民等)跟蹤市場能力相對較弱,彈性系數(shù)較小。此外,價格彈性矩陣還與用戶用電行為模式有關(guān),不同用電習(xí)慣和用電目的下價格彈性矩陣各異。
為了將負(fù)荷需求電價彈性關(guān)系計入電力負(fù)荷預(yù)測模型中,可采用圖1中的反饋模型。通過反饋修正預(yù)測值,當(dāng)△小于某一設(shè)定的精確度值時輸出,神經(jīng)網(wǎng)絡(luò)預(yù)測模型能較好滿足這一要求。此外,由于電價與氣候以及日類型之間的關(guān)系并沒有非常強的相關(guān)性,所以符合BP神經(jīng)網(wǎng)絡(luò)的初始條件。

圖1 反饋模型示意圖
2 負(fù)荷分解模型
根據(jù)地區(qū)負(fù)荷與電價的現(xiàn)實規(guī)律,從總負(fù)荷中分解出對電價不敏感的基礎(chǔ)負(fù)荷和受電價因素影響的電價敏感性負(fù)荷2部分,從而建立負(fù)荷分解模型:
=basic+price+random. (3)
式(3)中:為總負(fù)荷;basic為基礎(chǔ)負(fù)荷,反映負(fù)荷在較長持續(xù)時間內(nèi)某種總的發(fā)展趨勢,具有一定的穩(wěn)定性、周期性和季節(jié)性;price為電價敏感性負(fù)荷,反映電價因素對負(fù)荷變化的影響,是隨電價因素變化上下波動的負(fù)荷分量;random為誤差分量,包括由隨機因素而造成的負(fù)荷變化量和預(yù)測前2個負(fù)荷分量時所產(chǎn)生的誤差。
其中,基礎(chǔ)負(fù)荷包括趨勢分量和周期分量2部分。趨勢分量表征了一段時間內(nèi)負(fù)荷的某種持續(xù)發(fā)展趨向,一般受經(jīng)濟等因素的影響而不用考慮天氣、節(jié)假日和隨機因素,在短期負(fù)荷預(yù)測中可視趨勢分量為常數(shù)處理;周期分量則反映了負(fù)荷的季節(jié)性和周期性方面的循環(huán)變化。本文在電力公司常規(guī)負(fù)荷預(yù)測和某地區(qū)電力需求價格彈性研究的基礎(chǔ)上,對需求價格彈性曲線采用線性擬合后,運用公式(4)和(5)即可得到預(yù)測日的基礎(chǔ)負(fù)荷:
basic=-price. (4)
pric=×+. (5)
式(4)(5)中:為一日負(fù)荷,由實時負(fù)荷構(gòu)成24×1的矩陣=[1,2,…,24];為一日電價,由實時電價構(gòu)成24×1的矩陣=[1,2,…,24];和為線性擬合后的需求價格曲線參數(shù)矩陣,不同的用戶中和的數(shù)值也不同。
對于總數(shù)為的用戶群,有=[1,2,…,n],=[1,2,…,n],運用蒙特卡洛仿真方法,在其電力需求價格彈性的變化區(qū)間內(nèi)抽樣取出一隨機變量[n,n],代入公式(5)即可求出函數(shù)值price.當(dāng)獨立模擬的次數(shù)相當(dāng)多時,就可以通過計算出的price1,price2,,pricen,確定出函數(shù)price的概率分布和數(shù)學(xué)期望等多種統(tǒng)計參數(shù)。在price數(shù)學(xué)期望值的基礎(chǔ)上應(yīng)用公式(4)即可計算得到basic.另外,由于對需求價格彈性曲線線性化處理后,其中的乘法運算使得數(shù)據(jù)誤差被進一步放大,需要對所得數(shù)據(jù)進行平滑處理,才能使基礎(chǔ)負(fù)荷的計算結(jié)果更符合基礎(chǔ)負(fù)荷的一般性特征。
3 短期負(fù)荷預(yù)測模型
3.1 輸入輸出變量的選擇
根據(jù)上述對短期電力負(fù)荷特性的分析,本模型中采用帶有15個輸入變量和1個輸出變量的負(fù)荷預(yù)測模型,連續(xù)建模24次即可預(yù)測未來1 d每小時的負(fù)荷水平。模型的輸入和輸出變量如表1所示。
表1 BP神經(jīng)網(wǎng)絡(luò)的輸入輸出描述
類別編號描述 輸入變量負(fù)荷數(shù)據(jù)1~2預(yù)測點前1時刻和前2時刻負(fù)荷值 3~5前1 d的同一預(yù)測時刻點、同一預(yù)測點前1時刻和后1時刻負(fù)荷值 6~8前1周的同一預(yù)測時刻點、同一預(yù)測點前1時刻和后1時刻負(fù)荷值 電價數(shù)據(jù)9~12預(yù)測點電價、預(yù)測點前1時刻、預(yù)測點前兩時刻和后1時刻電價 13前1 d的同一預(yù)測時刻點電價 其他數(shù)據(jù)14預(yù)測日日類型 15預(yù)測日平均溫度 輸入變量1未來1 d每小時的負(fù)荷預(yù)測值
3.2 BP神經(jīng)網(wǎng)絡(luò)進行負(fù)荷預(yù)測輸出
在上述提出的負(fù)荷分離方法和神經(jīng)網(wǎng)絡(luò)基本建模思路基礎(chǔ)上,本文構(gòu)造了分離基礎(chǔ)負(fù)荷的BP神經(jīng)網(wǎng)絡(luò)負(fù)荷預(yù)測模型,其工作流程如圖2所示。
4 算例分析
利用上述方法,對美國PJM市場中的某地區(qū)2017-05-14進行未來1 d每小時的負(fù)荷預(yù)測,訓(xùn)練數(shù)據(jù)取2017-03—2017-04的歷史負(fù)荷數(shù)據(jù)。圖3為各種方法的負(fù)荷預(yù)測結(jié)果對比曲線。對于相同的BP神經(jīng)網(wǎng)絡(luò)預(yù)測模型,從對比數(shù)據(jù)及曲線中分析可知,不考慮電價因素的負(fù)荷預(yù)測時的誤差比較大,其平均絕對值百分誤差()為2.869 2%;考慮了電價因素以后為1.560 8%.將負(fù)荷中的基礎(chǔ)負(fù)荷部分分離后得到的預(yù)測結(jié)果精度更為精確,達(dá)到了1.368 9%,可見在電力市場環(huán)境下,實時電價與負(fù)荷需求間存在著密切聯(lián)系,特別是當(dāng)總負(fù)荷中分離出不受電價影響的基礎(chǔ)負(fù)荷后,考慮電價因素后的負(fù)荷預(yù)測結(jié)果也更精確。

圖2 分離基礎(chǔ)負(fù)荷的BP神經(jīng)網(wǎng)絡(luò)負(fù)荷預(yù)測模型
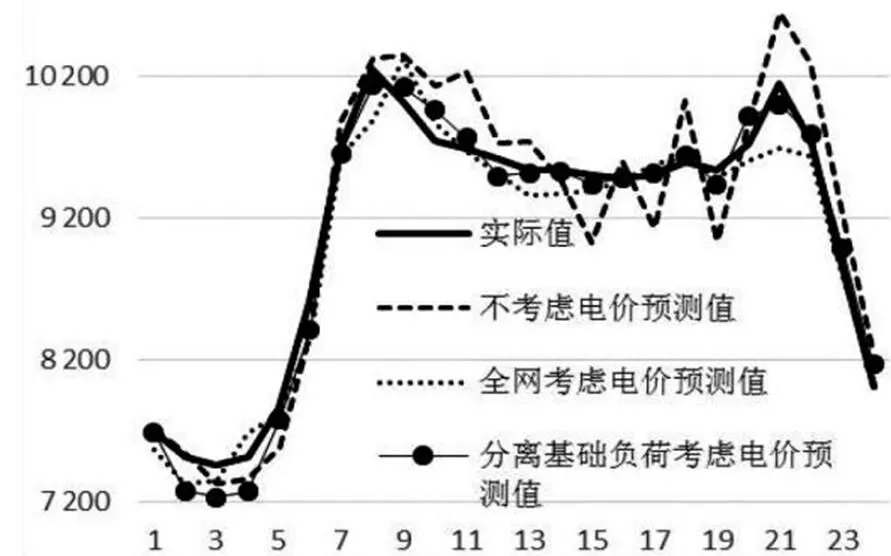
圖3 實際負(fù)荷與不同方法負(fù)荷預(yù)測結(jié)果
5 結(jié)束語
綜上所述,本文提出的短期負(fù)荷預(yù)測模型有助于評估柔性負(fù)荷的可調(diào)能力和可控容量,進一步提高分析預(yù)測質(zhì)量和準(zhǔn)確性水平,充分挖掘智能電網(wǎng)環(huán)境下負(fù)荷側(cè)資源,優(yōu)化電力資源配置,為電力系統(tǒng)運行的經(jīng)濟性和安全性提供有力的保證。
[1]康重慶,夏清,胡左浩,等.電力市場中預(yù)測問題的新內(nèi)涵[J].電力系統(tǒng)自動化,2004(18).
[2]顧明宏.揚州市電力負(fù)荷特性及DSM潛力分析[D].廣州:東南大學(xué),2005.
[3]林海英,李建榮,宣菊琴,等.鋼鐵行業(yè)負(fù)荷特性及需求側(cè)管理潛力分析[J].華東電力,2005(11).
2095-6835(2018)21-0039-02
U223
A
10.15913/j.cnki.kjycx.2018.21.039
〔編輯:張思楠〕

