基于灰色理論預測人口新政策對經濟發展的影響
朱家明,胡榴榴,王 楊,胡逸群
(安徽財經大學 a.統計與應用數學學院;b.國際經濟貿易學院,安徽 蚌埠 233030)
1971年,“有計劃地增長人口”被確定為我國既定的人口政策。這項特殊的人口政策在一定程度上控制了我國人口增長的速度,但也帶來了另一重大人口問題:過高的人口老齡化。我國政府改變人口政策,逐步放開生育政策,推行“全面二孩”政策。這一政策在社會各界引起了激烈討論。林杰等對基于不同政策對人口結構的影響進行了研究[1],李詠馨等基于綜合評價法對人口可持續發展模型進行了研究[2],本文基于Leslie矩陣和灰色預測模型,研究“全面二孩”政策對我國人口結構的影響。
一、基于Leslie模型分析新政策對我國未來人口的預測
(一)數據準備
利用“全面二孩”政策實施之前中國國家統計局公布的全國人口普查數據,根據最近五年(2012—2016)數據得出不同年齡階段的婦女生育人數,并計算出不同年齡階段婦女生育人數占總出生人數的比重(簡稱出生比),見表1。

表1 不同年齡階段婦女生育人數占總出生人數的比重
(二)研究方法
我們利用Matlab軟件建立Leslie矩陣[3],對我國2017—2030年人口情況進行預測分析。
將人口按年齡大小等間隔地劃分為若干個年齡組,假設人口的生育率與死亡率不隨時段k變化,只與年齡組有關。記存活率為Si(1-死亡率),生育率為bj。
人口數量為xi(k)的變化規律為:當時段k+1時,第一個年齡組的數量是各年齡組在時段k的生育數量之和;第i+1年齡組(i=1,2,…,m-1)的數量是時段k第i年齡組存活下來的數量。由此得到
(1)
xi+1(k+1)=sixi(k),k=0,1,2,…;i=1,2,…,m-1
(2)
其中(1)(2)是差分方程,記人口數量在時段k按年齡組的分布向量
x(k)=[x1(k),x2(k),…,xm(k)]T,k=0,1,2,…
則(1)(2)可表示為x(k+1)=Lx(k),k=0,1,2,…
當矩陣和年齡按年齡組的初始分布x(0)已知時,可以預測人口數量在時段k按年齡組的分布為x(k)=Lkx(0),k=1,2,…
通過使用Matlab軟件,依據往年的總人口、女性人口、出生嬰兒數等數據,計算出該年份的生育率、繁殖率、女性人口比率、存活率,建立Leslie矩陣L,通過公式計算出,如表2所示。

表2 2017—2030年我國總人口數(單位:億人)
同時利用該模型計算出(0—14歲、14—64歲、65歲及以上)的人口數量,見表3。
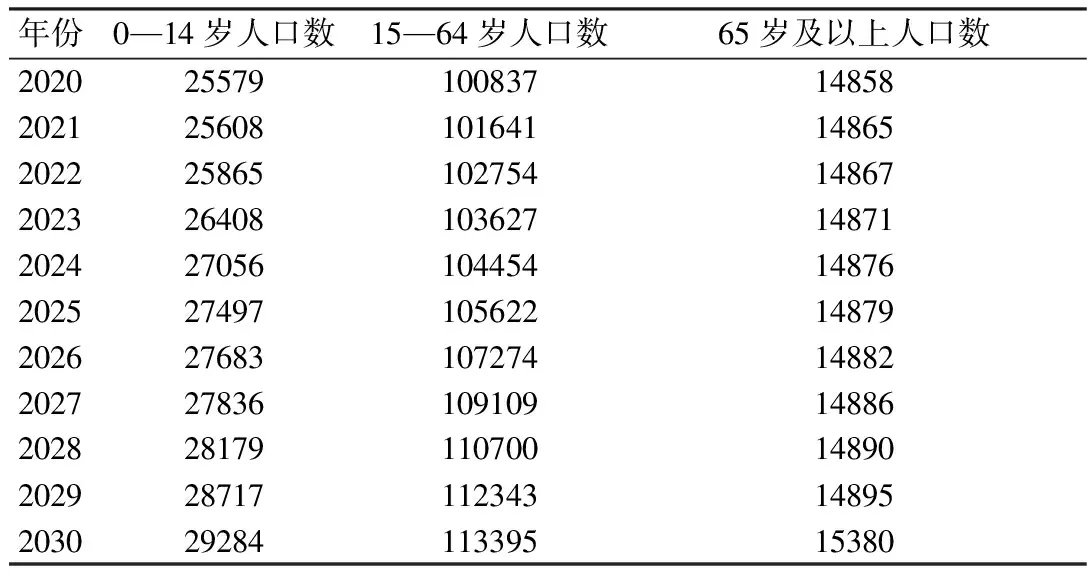
表3 “全面二孩”政策下2020—2030年中不同年齡結構 (單位:萬人)
(三)結果分析
將Leslie矩陣的結果(“全面二孩”政策下2017—2030年我國人口總人數)繪制成折線圖,如圖1所示。
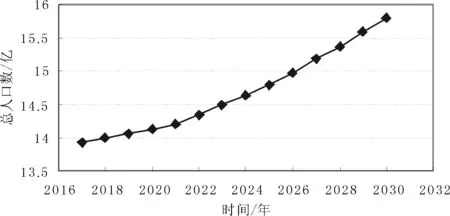
圖1 2017—2030年我國總人口數
從Leslie矩陣計算得出的結果可以看出,實施“全面二孩”政策之后,我國的人口總數顯著上升,且上升速度不斷變快,說明“全面二孩”政策實施下我國人口出生率有了顯著提升。由此可以得出,這一政策的實施對于我國人口紅利逐漸消失的現狀有積極影響。
二、基于多元回歸分析人口結構變化對經濟發展的影響
(一)數據準備
查找并整理得出過去20年我國人均GDP、0—14歲人口數、15—64歲人口數、65歲及以上人口數、總撫養比、少兒撫養比、老年撫養比、人口出生率、人口死亡率和人口自然增長率。
(二)研究方法
1.相關分析
以人均GDP為被解釋變量,分別以0—14歲人口數、15—64歲人口數、65歲及以上人口數、總撫養比、少兒撫養比、老年撫養比、人口出生率、人口死亡率和人口自然增長率為解釋變量,做相關分析,并得出線性值[3-4],見表4。
由R2線性值可以看出,0—14歲人口數、15—64歲人口數、65歲及以上人口數、少兒撫養比、老年撫養比、人口死亡率與人均GDP成較強的線性關系,總撫養比、人口出生率和人口自然增長率與人均GDP線性關系較弱,故而剔除總撫養比、人口出生率和人口自然增長率3個因素。
2.回歸分析
建立0—14歲人口數(X1)、15—64歲人口數(X2)、65歲及以上人口數(X3)、少兒撫養比(X4)、老年撫養比(X5)、人口死亡率(X6)與人均GDP(Y)的回歸方程[2,5],得出回歸方程如下:
Y=-94971.93-5.830X1+0.3965X2+26.7606X3+5910.311X4-19989.81X5+1016.823X6

表4 各變量的R2線性值
由回歸分析結果得出,F檢驗對應的概率值為0.00,小于0.05,各因素對方程的影響較為顯著。但由t檢驗可以看出15—64歲人口數(X2)、人口死亡率(X6)的t檢驗不通過,因而剔除這兩個因素再做回歸分析。得出新的回歸方程如下:
Y=-4673.53-5.72X1+30.59X3+5729.21X4-23882.49X5
做自相關檢驗發現0—14歲人口數(X1)與少兒撫養比(X4)相關性較強,65歲及以上人口數(X3)與老年撫養比(X5)相關性較強,因而對回歸模型進行調整,最終以0—14歲人口數(X1)、65歲及以上人口數(X3)為解釋變量,以人均GDP為被解釋變量,進行多元回歸分析。得出回歸方程如下:
Y=-89357.46+0.664598X1+8.781313X3
最終,把Leslie矩陣計算出的2020—2030年我國人口情況代入回歸方程,得出“全面二孩”政策實施下我國人均GDP情況,見表5。

表5 實施“全面二孩”政策下的人均GDP(單位:元)
(三)結果分析
從相關分析可以看出,人口結構的變化會對我國人均GDP產生影響,尤其是老年人口數量和老年撫養比對于人均GDP的影響尤為顯著;從多元回歸分析可以看出,近些年我國人均GDP一直呈上升趨勢。當然,影響人均GDP除人口結構以外還有其他多種因素,回歸分析的結果只能在一定程度上反映人口增長與經濟發展呈同方向變動,且這一發展狀況是基于我國特定國情的。
三、我國人口合理化發展的生育政策建議
(一)研究思路
首先預測出不實施“全面二孩”政策下我國的人口結構情況,并將人口結構情況代入多元回歸方程得出不實施人口政策下我國的經濟情況預測;然后將它與“全面二孩”政策實施下的經濟情況預測進行對比,進而給出合理化的生育政策建議。
(二)研究方法
根據收集到的1996—2015年我國人口結構情況,利用Matlab建立灰色預測模型[5-6],預測出實施“全面二孩”政策下2020—2030年我國人口結構的情況,見表6。
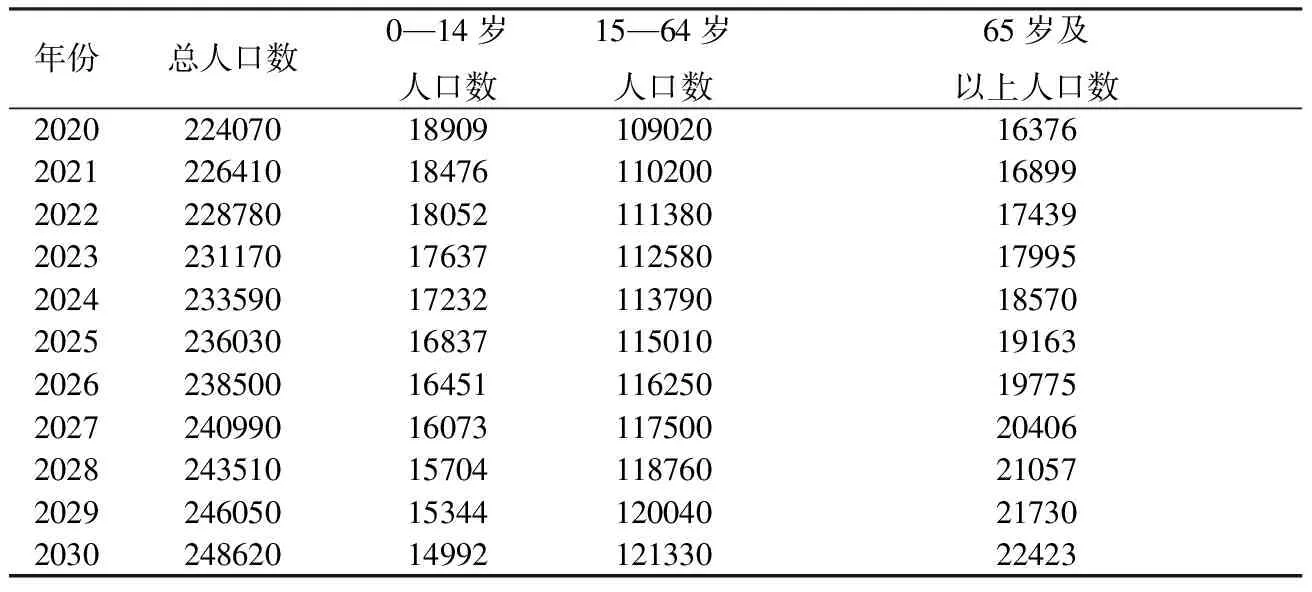
表6 “全面二孩”政策下2020—2030年我國人口結構(單位:萬人)
以0—14歲人口數、65歲及以上人口數為自變量,代入上述回歸方程對人均GDP進行預測,得出不實施“全面二孩”政策下2020—2030年我國人均GDP預測情況,見表7。

表7 不實施“全面二孩”政策下2020—2030年我國人均GDP(單位:元)
(三)結果分析
由回歸分析得出實施“全面二孩”政策與不實施“全面二孩”政策下我國人均GDP情況如圖2所示。
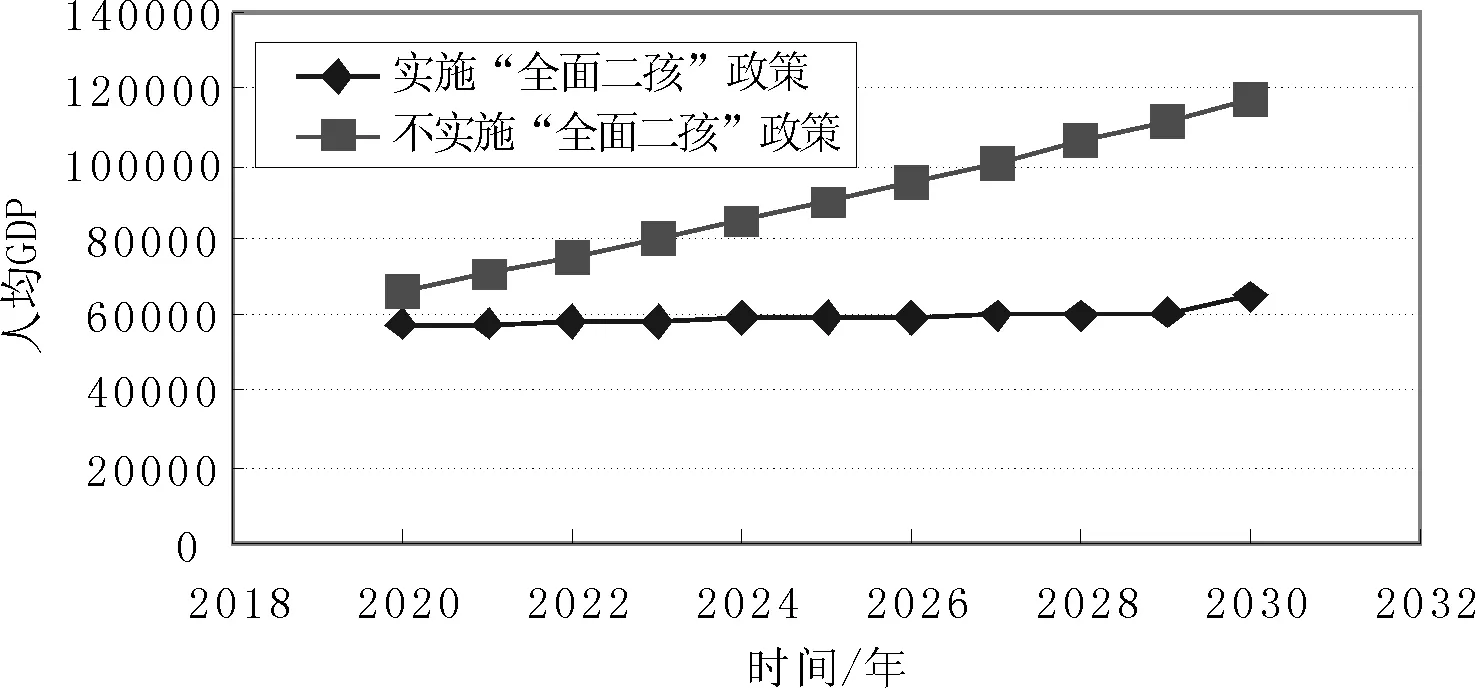
圖2 實施“全面二孩”政策與不實施“全面二孩”政策下我國人均GDP
根據回歸分析可以看出,無論是否實施“全面二孩”政策,我國人均GDP發展態勢都呈上升趨勢,但實施“全面二孩”政策下的人均GDP增長幅度明顯要低于不實施“全面二孩”政策下的人均GDP增長幅度。由此可以看出,從短期來看,“全面二孩”政策的實行可能會使得我國的經濟增長速度放緩,這可能是“全面二孩”政策實行后不斷增加的生育費用、嬰幼兒撫養費用等導致的。但從長期來看,“全面二孩”政策可以改變我國人口老齡化程度,改善我國的人口結構,提高我國勞動力數量,這是有利于我國經濟長期發展的。
綜上所述,關于我國的生育政策,給出以下建議[6]。
第一,要實施適當的“全面二孩”政策,輔之以一定程度的生育限制。過高的生育率除了降低人口老齡化,還會帶來高的社會撫養比,在短期內會減緩經濟發展的幅度。
第二,人口政策的實施需要結合民情。如果普遍社會生育率不高,人們生育積極性低,可以進行一定的鼓勵生育政策,人口老齡化是我國當前人口發展的重大問題,長期發展下去必然帶來社會撫養比提高,勞動力缺失等不利于經濟發展的現實問題。
第三,把握好實施生育政策的度,及時根據社會實際情況對生育政策進行調整;綜合考慮生育政策可能帶來的各方面影響,選取最為合理的生育政策。
第四,人口出生率不僅僅受到人口政策的影響,還會隨著社會環境、人們心理因素的變化不斷發生變化。因此,生育政策的選擇,還需考慮到心理因素的影響。
四、結束語
綜合利用Leslie矩陣、灰色預測模型對實施“全面二孩”政策和不實施“全面二孩”政策下我國人口數量和結構進行預測,同時利用回歸分析得出人口結構變動對我國經濟發展的影響,并將預測得出的人口結構代入回歸方程預測出我國未來的人均GDP。預測結果顯示,在不考慮其他因素的影響下,“全面二孩”政策的實施,在短期內會減緩我國經濟增長態勢;但從長期來看,這一政策的實施是有助于改善我國目前不合理的人口結構的。任何一個政策的實施都是具有兩面性的,在給我們帶來利益的同時也會有一定缺陷,我們要在協調發展的基礎上辨證地選擇政策,對于人口問題更應在可持續發展的基礎上用全面的眼光衡量。

