考慮軸承支撐剛度和齒輪軸變形的內嚙合齒廓修形研究*

，，

(1.湘潭江麓技工學校，湖南湘潭411105；2.湘潭大學，湖南湘潭411105)

0 引言

齒輪傳動是最具代表性的傳動機構，雖然其發展歷史較長，但在齒輪修形上，很多是根據經驗進行的，對修形位置和修形量的精準計算需要進一步開展研究[1]。之前的理論和實踐分析表明，適當的齒輪齒廓修形能人為地補償齒輪嚙合時輪齒彈性變形，抵消由于彈性變形產生的干涉，減少齒輪嚙入和嚙出沖擊，達到減震降噪的效果[2-5]。當前國內外主要采用經驗公式確定修形量，當采用經驗公式修形時，雖方法簡單，但由于考慮的因素單一，獲得的修形效果不好。有多種因素影響齒輪的嚙合，其中齒輪軸的軸承支撐剛度和彈性變形是影響齒輪嚙合的重要因素，計算齒輪的修形量時，需考慮以上兩因素。在分析原有修形方法的基礎上，考慮軸承剛度和彈性變形的影響，推導齒廓修形量計算公式和確定修形曲線[5]。

1 內齒輪當量齒形推導

在計算輪齒彈性變形時，目前應用較多的方法是石川修形公式，其中需用到當量齒形[6]，查閱眾多參考文獻以及資料，只有外齒輪當量齒形的計算方法，沒有關于內齒輪當量齒形的計算公式[5]，開展的研究對象為內外齒輪嚙合，故需對內齒輪當量齒形進行推導。

1.1 內齒輪當量齒頂厚Sk和當量齒高h

分析圖1所示的內齒輪幾何關系可知，當量齒頂厚為：

Sk=2rasinφ

(1)

式中，ra為齒頂圓半徑，φ為展開角。

內齒輪漸開線在齒頂處的展開角小于標準壓力角，因此有：

(2)

式中，αa為齒頂處漸開線壓力角，s為分度圓齒厚，r為分度圓半徑，α為標準壓力角。將(2)式代入(1)式得：

(3)

由圖1所示幾何關系，內齒輪當量齒高為：

(4)

式中，rf為齒根圓直徑。

1.2 嚙合接觸載荷點高度hx

如圖2所示，可得：

(5)

式中，αx為瞬時嚙合接觸點處壓力角，μ為某時刻嚙合接觸處載荷作用角。

圖2 內齒輪當量齒形載荷作用點確定示意圖

1.3 載荷作用角μ

如圖3所示，可得：

αx+μ=φ

(6)

(7)

將式(7)代入式(6)得：

(8)

圖3 內齒輪當量齒形載荷作用角示意圖

1.4 矩形部分高度hr和齒根厚Sf

對于內齒輪，不僅齒根圓半徑大于基圓半徑，有效齒根圓半徑也大于基圓半徑，當量齒形的梯形與矩形的交點為有效齒根圓與齒廓交點，根據圖2可得：

(9)

(10)

式中，rf為齒根圓半徑，αf為齒根圓處壓力角。

2 嚙合點位置變化的分析

圖4 支承軸承變形與軸變形的 疊加的示意圖

在計算齒輪輪齒的彈性變形時，往往認為軸和軸承為剛性體，忽略這部分彈性變形對輪齒變形的影響。但實際上軸和軸承都為彈性體，兩者會同時發生彈性變形，如圖4所示。

當承受徑向載荷，先假設支撐齒輪軸的軸承是剛性而軸是彈性，齒輪軸的撓曲角為θ1，撓度值為w1；然后假設軸承具有彈性而軸是剛性時，齒輪軸的撓曲角為θ2，撓度值為w2。兩種情況下撓曲角相加，為軸系總的撓曲角；兩種情況下撓度相加，為軸系總的撓度，即：

θ=θ1+θ2

(11)

w=w1+w2

(12)

齒輪軸發生彈性變形時軸端的撓度值為w1和撓曲角θ1，可以根據材料力學方法求得。由于軸承彈性位移引起的軸端徑向位移量w2和撓曲角θ2與軸承剛度有關，如圖4(c)所示，假設A、B處軸承剛度分別為K1、K2，則由支撐變形引起的軸端徑向位移量w2和撓曲角θ2分別為：

(13)

(14)

支撐剛度的計算方法很多，劉顯軍、洪軍等人[7]采用有限元迭代法進行求解，該方法考慮了預緊載荷的影響，通過迭代能夠很好的保證求解精度，現采用兩位學者的方法來計算軸承的支撐剛度。

支撐軸承和軸的變形導致傳動齒輪傾斜，從而改變兩嚙合齒輪嚙合點的位置，使嚙合接觸線偏移或轉動，如圖5。從單個齒輪看，雖然輪齒上的實際嚙合接觸線相對于理論嚙合接觸線發生了偏離，但仍然認為實際嚙合接觸線為一條直線，并與理論嚙合接觸線的夾角為θ，該夾角是兩嚙合齒輪因受載使齒輪軸傾斜，兩齒輪軸之間的夾角，理想情況下為0。

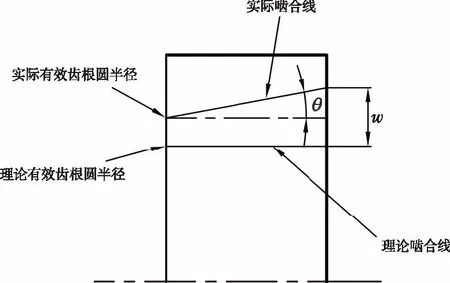
圖5 齒根圓實際半徑與理論半徑

根據軸的撓度值，沿直徑大的方向，嚙合接觸線移動的距離為w，將兩嚙合齒輪嚙合點投影在軸上，分別計算兩軸在投影點處的撓度值，w等于撓度值之和。當然，對于內嚙合齒輪，內齒輪的支撐可認為是剛性支撐，只考慮外齒輪軸的傾斜。考慮實際嚙合接觸線傾斜于理想嚙合接觸線，使得載荷作用點偏移，從而使齒根圓有效半徑和輪齒接觸齒寬都發生了改變，如果要采用石川修形公式求齒輪修形曲線時，應對參數進行如下修改。

(15)

(16)

b′=b*cosθ

(17)

3 齒廓最大修形量計算

根據直齒輪的嚙合綜合剛度理論，齒輪在嚙合過程中，嚙入和嚙出時刻的綜合嚙合剛度最小，從而齒輪輪齒的綜合彈性變形量為最大。

齒輪由單齒嚙合進入雙齒嚙合或雙齒嚙合進入單齒嚙合時，輪齒會產生一個沿嚙合線方向上的彈性位移δs[8]，如圖6所示。嚙入時彈性變形最大，計算此刻的彈性變形量，即可作為齒廓的最大修形量，齒輪的修形就是從理論上補償這一彈性變形δs，從而減小齒輪嚙入和嚙出時的沖擊[9]。

圖6 齒輪嚙入時彈性變形

根據石川修形公式，齒輪副在載荷作用下發生的彈性變形為[8]：

(18)

式中：δbr為當量齒形長方形部分的彎曲變形量，δs為由剪力產生的變形量，δbt為當量齒形梯形部分的變形量，δg為基礎部分傾斜產生的變形量，δp為齒面接觸變形量。

由于是計算嚙入時刻齒輪輪齒的彈性變形，所以，外齒輪齒頂處為載荷作用起點，而內齒輪的有效齒根圓處為載荷作用起點，由于齒輪在加工中難免存在誤差，故齒廓最大修形量為：

Δmax=δ∑+δi

(19)

式中：δi為由于制造誤差的原因，所引起的齒輪在嚙入嚙出時產生的干涉量，由下式獲得：

δi=cosαfpt

(20)

式中：α為齒輪標準壓力角，fpt為齒輪的周節極限偏差。

4 修形曲線的確定

齒廓上修形部分的修形量和位置通過齒廓修形曲線來表達[10]，即使采用相等的最大修形量，但如果修形曲線不同，對提高齒輪嚙合性能的影響也不一樣，為獲得最好的修形效果，確定科學的修形曲線也非常關鍵。齒廓的修形曲線公式為[9]：

(21)

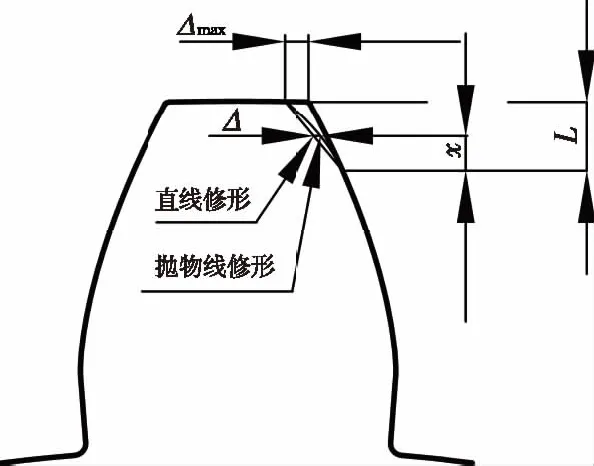
圖7 齒廓修形示意圖

式中：Δ為齒輪在某一嚙合位置上的修形量；L為齒輪修形長度；Δmax為齒廓最大修形量；x為兩齒輪嚙合位置相對于單雙齒嚙合切換點處的坐標；b為冪指數，當b=1時，齒廓的修形曲線變為直線，b=2時，齒廓的修形曲線為拋物線，實際中經常采用這兩種修形曲線對齒輪進行修形，如圖7。

朱傳敏等[11]試驗證明，如果齒輪傳動在輕載低速的情況，修形曲線對齒輪的嚙合性能影響效果不大，但在高速和重載的情況下，對齒廓進行拋物線修形，能顯著改善齒輪的傳動性能，并且優于其他曲線的修形。

5 齒廓修形長度的確定

按修形起始點的位置不同，齒廓的修形長度分為長修形和短修形兩種[9-10，12]。如圖8所示，沿著嚙合線，長修形為嚙合的上下界點到雙齒嚙合的起始點或者終結點處[9]，如圖中B2D或者B1C。

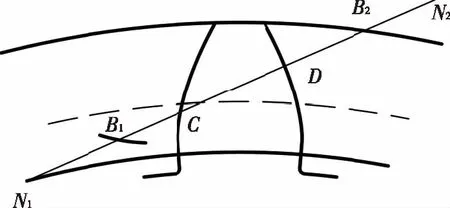
圖8 修形長度示意圖

長修形長度L可由式(22)計算：

(22)

式中：Z為嚙合線長度，pb為端面基節。

采用長修形，齒廓修形曲線將更加平滑，齒輪在高速重載情況下，多采用長修形。本文所研究的變槳輸出齒輪嚙合為重載情況，擬齒輪采用長修形。

6 齒廓修形量計算程序開發

由于石川修形公式比較復雜，如果想通過這種理論計算的方法得到齒廓修形量，那將是一件非常繁瑣且易出錯的工作。基于Visual C++平臺，開發計算程序。通過該程序，只要在程序界面上輸入齒輪的基本參數，便可通過修正了的石川修形公式，計算出齒廓最大修形量，所開發程序界面如圖9所示。由于齒輪支承和軸結構尺寸變化大，使用該修形軟件時，應參考前面所提方法，先計算軸的撓度和撓曲角，在齒輪軸變形參數框中輸入，該軟件便自動計算出最大修形量。

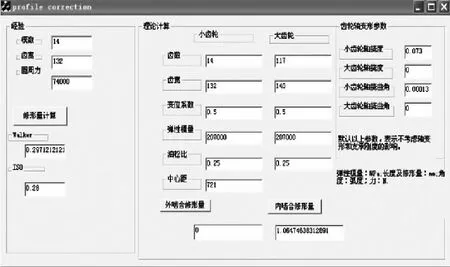
圖9 所開發的齒廓修形量計算程序界面

7 齒廓修形設計應用舉例

XE93變槳減速器輸出軸齒輪及其配對內齒輪的模數m=14，齒數z1=14、z2=117，變位系數x1=0.5=x2，齒輪使用材料20CrMnTi。將這些參數輸入到程序，并將計算得到的小齒輪軸的撓度0.073和撓曲角0.00013輸入，得到這對齒輪嚙入時刻齒廓的綜合彈性變形量如圖9所示，為1.064 mm。按照6級精度考慮制造齒輪，誤差帶入的修形干涉量為0.024，從而得到齒廓最大修形量為：

Δmax=δs+δi=1.088 mm

(23)

當修形量確定后，考慮減速器的工況，采用拋物線修形和長修形方式。

在SolidWorks中，根據修形曲線對齒輪副建模，首先在工程分析軟件(Abaqus)進行有限元分析，得到修形前后齒輪副在嚙入時刻的應力云圖如圖10所示；然后在動力學分析軟件(Adams)中進行動力學分析，得到內齒輪轉速如圖11。

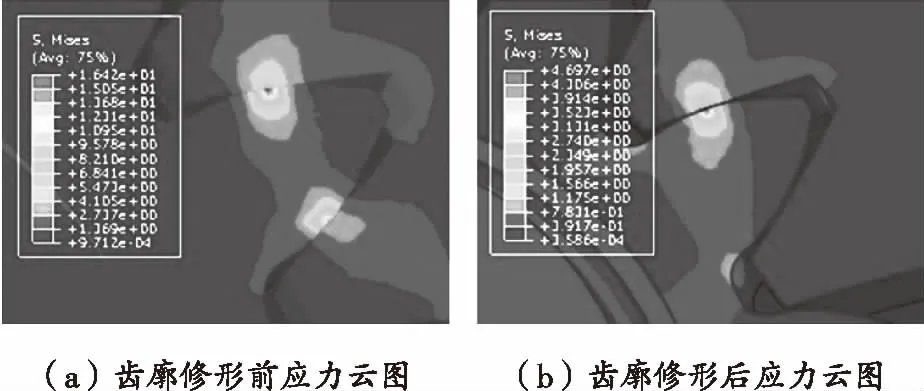
圖10 修形前后齒輪應力云圖對比

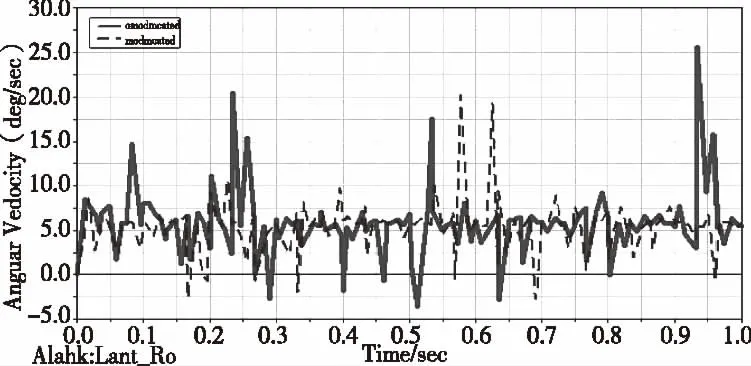
圖11 內齒輪轉速隨時間變化關系

通過圖10可以發現，當齒輪沒有修形，齒輪嚙入時，在齒廓兩側出現了應力集中現象；齒輪修形后，僅單側出現應力集中現象，并且應力值成倍下降。可見通過齒廓修形，改善了齒輪嚙入嚙出時載荷沖擊，減少應力集中。

圖11中實線表示內齒輪沒有修形時轉速波動情況；虛線表示內齒輪進行齒廓修形后內齒輪轉速的波動情況。從圖可以看出，對齒輪修形后，轉速比沒有修形時要平穩，從而顯著降振動和噪音。所以從數值仿真分析結果來看，齒廓修形改善了齒輪傳動效果。

在變槳減速器投入批量生產之前，為驗證其可靠性與穩定性，需對其進行性能試驗，試驗臺原理如圖12。

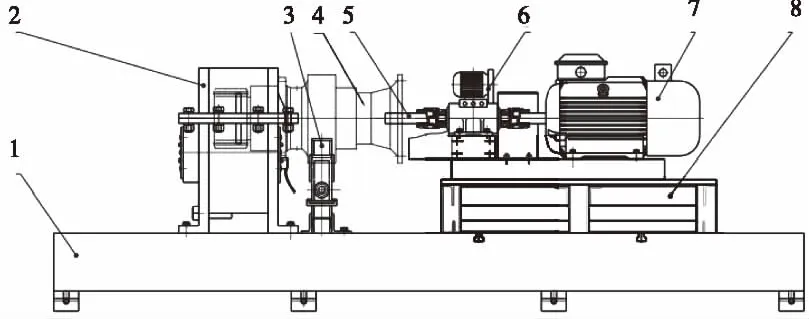
1-試驗臺底座；2-對扭傳動箱；3-支架；4-被試件； 5-驅動軸；6-轉矩轉速傳感器；7-電機；8-可調支架。 圖12 減速器性能測試試驗臺的結構示意圖

按照原理圖搭建的試驗臺如圖13，采用兩個變槳減速器同時開展試驗，一為被試件，另一個為陪試件。兩個電機，一為驅動電機，一為負載電機，兩個電機對扭，兩電機采用兩個變頻器控制，負載電機通過變頻器，功率回饋到電網，從而使試驗臺的能耗很低。在電機和減速器之間都裝有轉矩和轉速傳感器，通過這兩個傳感器可得到驅動功率和負載功率，從而可計算變槳減速器的傳動效率。在變槳加速器的相應位置布置振動傳感器和溫度傳感器等，通過采集到的數據對減速器的傳動性能進行評定。

圖13 減速器性能試驗臺

在試驗臺上，按額定轉速和額定載荷對變槳減速器進行了200小時試驗，試驗結束后，取下齒輪輸出軸，洗去油污后，對齒面進行仔細觀察，發現齒輪的磨損非常少，沒發現明顯的邊緣接觸現象，看不到任何點蝕。測量了齒輪的公法線長度，與原檢測前幾乎沒有變化。證明通過修正后的石川修形公式所得到的修形量和修形曲線是可靠的。

8 結論

1)為對內齒輪嚙合的齒輪副進行齒廓修形，必須首先計算其當量齒形。

2)考慮了齒輪軸軸承支撐剛度和齒輪軸彈性變形對齒輪輪齒彈性變形的影響，正確的修正了石川修形公式中三個重要參數。

3)通過編程計算得到了齒廓修形量，并以拋物線長修形為其修形方式。通過ABAQUS和ADMAS的數值仿真分析表明，修形齒輪有明顯優于未修形齒輪的傳動性能。